人教版(2019)数学选择性必修三8.3.1分类变量与列联表课件(共27张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修三8.3.1分类变量与列联表课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 881.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 10:50:13 | ||
图片预览








文档简介
(共27张PPT)
8.3.1 分类变量与列联表
高二
选择性必修三
本节目标
1.通过实例,理解2×2列联表的统计意义.
2.理解判断两个分类变量是否有关系的常用方法.
预习课本124~127,思考并完成以下问题
(1) 什么是分类变量?什么是列联表?
(2) 等高堆积条形图分析变量的关系有什么优点?
课前预习
1.分类变量中的变量与函数中的变量是同一概念. ( )
课前小测
×
分类变量中的变量是指一定范围内的两种现象或性质,与函数中的变量不是同一概念.
2.列联表中的数据是两个分类变量的频数.( )
√
3.列联表、频率分析法、等高条形图都可初步分析两分类变量是否有关系.( )
√
A.近视 B.成绩
C.血压 D.饮酒
有近视与不近视两种类别
1.下列不是分类变量的是( )
有异常、正常两种类别
有饮酒与不饮酒两种类别
B
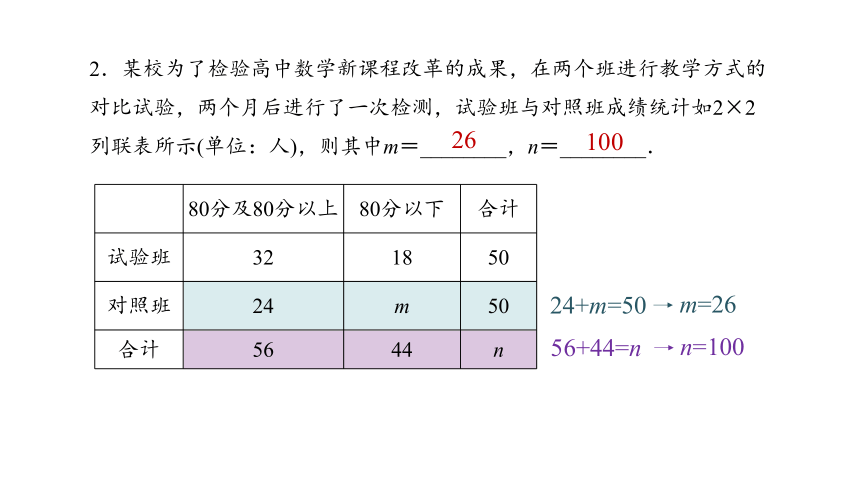
2.某校为了检验高中数学新课程改革的成果,在两个班进行教学方式的对比试验,两个月后进行了一次检测,试验班与对照班成绩统计如2×2列联表所示(单位:人),则其中m=________,n=________.
80分及80分以上 80分以下 合计
试验班 32 18 50
对照班 24 m 50
合计 56 44 n
24+m=50
m=26
56+44=n
n=100
26
100
新知探究
1.分类变量
我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量,分类变量的取值可以用______表示.
实数
例如,学生所在的班级可以用1,2,3等表示,
男性、女性可以用1,0表示,等等.
在很多时候,这些数值只作为编号使用,并没有通常的大小和运算意义.本节我们主要讨论取值于{0,1}的分类变量的关联性问题.
注意
这里所说的变量取值不一定是具体的数值,例如:性别变量,其取值为男和女两种.
2.2×2列联表
在实践中,由于保存原始数据的成本较高,人们经常按研究问题的需要,将数据分类统计,并做成表格加以保存,我们将这类数据统计表称为2×2列联表,2×2列联表给出了成对分类变量数据的交叉分类频数.
一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其2×2列联表为
y1 y2 合计
x1 a b a+b
x2 c d c+d
合计 a+c b+d a+b+c+d
3. 等高堆积条形图
等高条形图和表格相比,更能直观地反映出两个分类变量间是否相互影响,常用等高条形图展示列联表数据的频率特征,依据频率稳定于概率的原理,我们可以推断结果.
等高条形图
题型突破
典例深度剖析 重点多维探究
题型一 用2×2列联表分析两分类变量间的关系
[例1] 在对人们饮食习惯的一次调查中,共调查了124人,其中六十岁以上的70人,六十岁以下的54人.六十岁以上的人中有43人的饮食以蔬菜为主,另外27人则以肉类为主;六十岁以下的人中有21人饮食以蔬菜为主,另外33人则以肉类为主.请根据以上数据作出饮食习惯与年龄的列联表,并利用与判断二者是否有关系.
2×2列联表如下:
年龄在六十岁以上 年龄在六十岁以下 合计
饮食以蔬菜为主 43 21 64
饮食以肉类为主 27 33 60
合计 70 54 124
将表中数据代入公式得
= =0.671875
显然,二者数据具有较为明显的差异,据此可以在某种程度上认为饮食习惯与年龄有关.
= =0.45.
[例1] 在对人们饮食习惯的一次调查中,共调查了124人,其中六十岁以上的70人,六十岁以下的54人.六十岁以上的人中有43人的饮食以蔬菜为主,另外27人则以肉类为主;六十岁以下的人中有21人饮食以蔬菜为主,另外33人则以肉类为主.请根据以上数据作出饮食习惯与年龄的列联表,并利用与判断二者是否有关系.
总结提升
(2)利用2×2列联表分析两个分类变量间的关系时,首先要根据题中数据获得2×2列联表,然后根据频率特征,即将与(与)的值相比,直观地反映出两个分类变量间是否相互影响,但方法较粗劣.
(1)作2×2列联表时,关键是对涉及的变量分清类别.计算时要准确无误.
1. 假设有两个分类变量X与Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表为:
y1 y2
x1 10 18
x2 m 26
则当m取下面何值时,X与Y的关系最弱( )
A.8 B.9 C.14 D.19
跟踪训练
由10×26≈18m,解得m≈14.4,
所以当m=14时,X与Y的关系最弱.
C
[例2] 某学校对高三学生作了一项调查发现:在平时的模拟考试中,性格内向的学生426人中有332人在考前心情紧张,性格外向的学生594人中有213人在考前心情紧张,作出等高条形图,利用图形判断考前心情紧张与性格类型是否有关系.
性格内向 性格外向 合计
考前心情紧张 332 213 545
考前心情不紧张 94 381 475
合计 426 594 1 020
题型二 用等高堆积条形图分析两分类变量间的关系
作列联表如下:
相应的等高堆积条形图如图所示:
图中阴影部分表示考前心情紧张与考前心情不紧张中性格内向的人数的比例,从图中可以看出考前心情紧张的样本中性格内向的人数占的比例比考前心情不紧张样本中性格内向的人数占的比例高,可以认为考前心情紧张与性格类型有关.
总结提升
利用等高堆积条形图判断两个分类变量是否相关的步骤
2. 在调查的480名男人中有38人患色盲,520名女人中有6名患色盲,试利用图形来判断色盲与性别是否有关?
根据题目给出的数据作出如下的列联表:
色盲 不色盲 合计
男 38 442 480
女 6 514 520
合计 44 956 1000
跟踪训练
根据列联表作出相应的等高堆积条形图:
从等高堆积条形图来看,在男人中患色盲的比例要比在女人中患色盲的比例大得多,因此,我们认为患色盲与性别是有关系的.
随堂检测
1.与表格相比,能更直观地反映出相关数据总体状况的是( )
A.列联表 B.散点图
C.残差图 D.等高堆积条形图
D
2.在一项有关医疗保健的社会调查中,发现调查的男性为530人,女性为670人,其中男性中喜欢吃甜食的为117人,女性中喜欢吃甜食的为492人,请列出性别与喜欢吃甜食的2×2列联表.
喜欢吃甜食 不喜欢吃甜食 合计
男 117 413 530
女 492 178 670
合计 609 591 1200
3.根据如图所示的等高堆积条形图可知吸烟与患肺病________关系(填“有”或“没有”).
从等高条形图上可以明显地看出吸烟患肺病的频率远远大于不吸烟患肺病的频率.
有
4.(多空题)下面是一个2×2列联表:
则表中a=________,b=__________.
a+21=73
52
y1 y2 合计
x1 a 21 73
x2 2 25 27
合计 b 46 100
a+2=b
54
5.为考察某种药物预防疾病的效果进行动物试验,得到如下列联表:
患病 未患病 合计
服用药 10 45 55
未服用药 20 30 50
合计 30 75 105
试用等高条形图分析服用药和患病之间是否有关系.
根据列联表所给的数据可得出
服用药患病的频率为≈0.18,
未服用药患病的频率为=0.4,
两者的差距是|0.18-0.4|=0.22,两者相差很大,
作出等高条形图如图所示,因此服用药与患病有关系.
本课小结
1.通过本节课的学习,进一步提升数学抽象、直观想象及数据分析素养.
2.列联表与等高堆积条形图
列联表由两个分类变量之间频率大小的差异说明这两个变量之间是否有相关关系;
等高堆积条形图能形象直观地反映它们之间的差异,进而推断它们之间是否具有相关关系.
通过本节课,你学会了什么?
8.3.1 分类变量与列联表
高二
选择性必修三
本节目标
1.通过实例,理解2×2列联表的统计意义.
2.理解判断两个分类变量是否有关系的常用方法.
预习课本124~127,思考并完成以下问题
(1) 什么是分类变量?什么是列联表?
(2) 等高堆积条形图分析变量的关系有什么优点?
课前预习
1.分类变量中的变量与函数中的变量是同一概念. ( )
课前小测
×
分类变量中的变量是指一定范围内的两种现象或性质,与函数中的变量不是同一概念.
2.列联表中的数据是两个分类变量的频数.( )
√
3.列联表、频率分析法、等高条形图都可初步分析两分类变量是否有关系.( )
√
A.近视 B.成绩
C.血压 D.饮酒
有近视与不近视两种类别
1.下列不是分类变量的是( )
有异常、正常两种类别
有饮酒与不饮酒两种类别
B
2.某校为了检验高中数学新课程改革的成果,在两个班进行教学方式的对比试验,两个月后进行了一次检测,试验班与对照班成绩统计如2×2列联表所示(单位:人),则其中m=________,n=________.
80分及80分以上 80分以下 合计
试验班 32 18 50
对照班 24 m 50
合计 56 44 n
24+m=50
m=26
56+44=n
n=100
26
100
新知探究
1.分类变量
我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量,分类变量的取值可以用______表示.
实数
例如,学生所在的班级可以用1,2,3等表示,
男性、女性可以用1,0表示,等等.
在很多时候,这些数值只作为编号使用,并没有通常的大小和运算意义.本节我们主要讨论取值于{0,1}的分类变量的关联性问题.
注意
这里所说的变量取值不一定是具体的数值,例如:性别变量,其取值为男和女两种.
2.2×2列联表
在实践中,由于保存原始数据的成本较高,人们经常按研究问题的需要,将数据分类统计,并做成表格加以保存,我们将这类数据统计表称为2×2列联表,2×2列联表给出了成对分类变量数据的交叉分类频数.
一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其2×2列联表为
y1 y2 合计
x1 a b a+b
x2 c d c+d
合计 a+c b+d a+b+c+d
3. 等高堆积条形图
等高条形图和表格相比,更能直观地反映出两个分类变量间是否相互影响,常用等高条形图展示列联表数据的频率特征,依据频率稳定于概率的原理,我们可以推断结果.
等高条形图
题型突破
典例深度剖析 重点多维探究
题型一 用2×2列联表分析两分类变量间的关系
[例1] 在对人们饮食习惯的一次调查中,共调查了124人,其中六十岁以上的70人,六十岁以下的54人.六十岁以上的人中有43人的饮食以蔬菜为主,另外27人则以肉类为主;六十岁以下的人中有21人饮食以蔬菜为主,另外33人则以肉类为主.请根据以上数据作出饮食习惯与年龄的列联表,并利用与判断二者是否有关系.
2×2列联表如下:
年龄在六十岁以上 年龄在六十岁以下 合计
饮食以蔬菜为主 43 21 64
饮食以肉类为主 27 33 60
合计 70 54 124
将表中数据代入公式得
= =0.671875
显然,二者数据具有较为明显的差异,据此可以在某种程度上认为饮食习惯与年龄有关.
= =0.45.
[例1] 在对人们饮食习惯的一次调查中,共调查了124人,其中六十岁以上的70人,六十岁以下的54人.六十岁以上的人中有43人的饮食以蔬菜为主,另外27人则以肉类为主;六十岁以下的人中有21人饮食以蔬菜为主,另外33人则以肉类为主.请根据以上数据作出饮食习惯与年龄的列联表,并利用与判断二者是否有关系.
总结提升
(2)利用2×2列联表分析两个分类变量间的关系时,首先要根据题中数据获得2×2列联表,然后根据频率特征,即将与(与)的值相比,直观地反映出两个分类变量间是否相互影响,但方法较粗劣.
(1)作2×2列联表时,关键是对涉及的变量分清类别.计算时要准确无误.
1. 假设有两个分类变量X与Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表为:
y1 y2
x1 10 18
x2 m 26
则当m取下面何值时,X与Y的关系最弱( )
A.8 B.9 C.14 D.19
跟踪训练
由10×26≈18m,解得m≈14.4,
所以当m=14时,X与Y的关系最弱.
C
[例2] 某学校对高三学生作了一项调查发现:在平时的模拟考试中,性格内向的学生426人中有332人在考前心情紧张,性格外向的学生594人中有213人在考前心情紧张,作出等高条形图,利用图形判断考前心情紧张与性格类型是否有关系.
性格内向 性格外向 合计
考前心情紧张 332 213 545
考前心情不紧张 94 381 475
合计 426 594 1 020
题型二 用等高堆积条形图分析两分类变量间的关系
作列联表如下:
相应的等高堆积条形图如图所示:
图中阴影部分表示考前心情紧张与考前心情不紧张中性格内向的人数的比例,从图中可以看出考前心情紧张的样本中性格内向的人数占的比例比考前心情不紧张样本中性格内向的人数占的比例高,可以认为考前心情紧张与性格类型有关.
总结提升
利用等高堆积条形图判断两个分类变量是否相关的步骤
2. 在调查的480名男人中有38人患色盲,520名女人中有6名患色盲,试利用图形来判断色盲与性别是否有关?
根据题目给出的数据作出如下的列联表:
色盲 不色盲 合计
男 38 442 480
女 6 514 520
合计 44 956 1000
跟踪训练
根据列联表作出相应的等高堆积条形图:
从等高堆积条形图来看,在男人中患色盲的比例要比在女人中患色盲的比例大得多,因此,我们认为患色盲与性别是有关系的.
随堂检测
1.与表格相比,能更直观地反映出相关数据总体状况的是( )
A.列联表 B.散点图
C.残差图 D.等高堆积条形图
D
2.在一项有关医疗保健的社会调查中,发现调查的男性为530人,女性为670人,其中男性中喜欢吃甜食的为117人,女性中喜欢吃甜食的为492人,请列出性别与喜欢吃甜食的2×2列联表.
喜欢吃甜食 不喜欢吃甜食 合计
男 117 413 530
女 492 178 670
合计 609 591 1200
3.根据如图所示的等高堆积条形图可知吸烟与患肺病________关系(填“有”或“没有”).
从等高条形图上可以明显地看出吸烟患肺病的频率远远大于不吸烟患肺病的频率.
有
4.(多空题)下面是一个2×2列联表:
则表中a=________,b=__________.
a+21=73
52
y1 y2 合计
x1 a 21 73
x2 2 25 27
合计 b 46 100
a+2=b
54
5.为考察某种药物预防疾病的效果进行动物试验,得到如下列联表:
患病 未患病 合计
服用药 10 45 55
未服用药 20 30 50
合计 30 75 105
试用等高条形图分析服用药和患病之间是否有关系.
根据列联表所给的数据可得出
服用药患病的频率为≈0.18,
未服用药患病的频率为=0.4,
两者的差距是|0.18-0.4|=0.22,两者相差很大,
作出等高条形图如图所示,因此服用药与患病有关系.
本课小结
1.通过本节课的学习,进一步提升数学抽象、直观想象及数据分析素养.
2.列联表与等高堆积条形图
列联表由两个分类变量之间频率大小的差异说明这两个变量之间是否有相关关系;
等高堆积条形图能形象直观地反映它们之间的差异,进而推断它们之间是否具有相关关系.
通过本节课,你学会了什么?
