苏教版(2019)必修第一册7.1 角与弧度7.1.1 任意角 课件(共26张PPT)
文档属性
| 名称 | 苏教版(2019)必修第一册7.1 角与弧度7.1.1 任意角 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第7章
7.1
角与弧度
7.1.1 任意角
学习目标
1.理解任意角的概念,学会在平面内建立适当的坐标系来讨论任意角.
2.能在0°到360°范围内,找出一个与已知角终边相同的角,并判定其为第几象限角.
3.能写出与任一已知角终边相同的角的集合.
核心素养:数学抽象、数学运算、直观想象
新知学习
一 任意角的概念
1定义
一个角可以看作平面内一条射线绕着它的端点从
一个位置旋转到另一个位置所形成的图形.
射线的端点称为角的顶点,射线旋转的开始位置和终止位置称为角的始边和终边.
2角的表示
在不引起混淆的前提下,将“角α”或“∠α”简记作α.如图提示
在画图时,常用带箭头的弧来表示旋转的方向.
3角的分类
正角:按逆时针方向旋转所形成的角;
负角:按顺时针方向旋转所形成的角;
零角:一条射线没有作任何旋转.
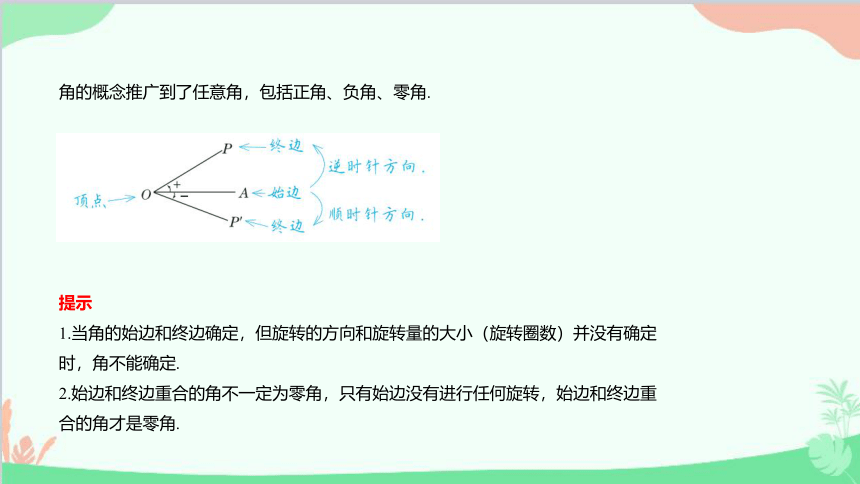
角的概念推广到了任意角,包括正角、负角、零角.
提示
1.当角的始边和终边确定,但旋转的方向和旋转量的大小(旋转圈数)并没有确定时,角不能确定.
2.始边和终边重合的角不一定为零角,只有始边没有进行任何旋转,始边和终边重合的角才是零角.
示例[多选题]在下列说法中,说法错误的是( )
A.小于180°的角是钝角、直角或锐角
B.始边和终边重合的角是零角
C.钟表的时针旋转而成的角是负角
D.零角的始边和终边重合
解析 A.小于180°的角可能是钝角,直角或锐角,也可能是零角或负角,不正确;
B.始边和终边重合的角相差360°的整数倍,可能是零角,也可能不是零角,不正确;
C.钟表的时针是顺时针旋转而成的角,因而是负角,正确;
D.零角的始边未做任何旋转,因而和终边重合,正确.
AB
二 象限角、终边相同角
1定义
为了便于研究,以角的顶点为坐标原点,角的始边为x轴非负半轴,建立平面直角坐标系,这样,角的终边(除端点外)在第几象限,就说这个角是第几象限角.
如果角的终边在坐标轴上,这个角不属于任何象限,就说这个角为轴线角.
2与角α终边相同的角的集合
一般地,与α终边相同的角的集合为{β|β=k·360°+α,k∈Z}.
解读(1)α是任意角.
(2)“k∈Z”有三层含义:
①特殊性:每取一个整数值就对应一个具体的角.
②一般性:表示所有与角α终边相同的角(包括α自身).
③从几何意义上看,k表示角的终边按一定的方向旋转的圈数,k取正整数时,逆时针方向旋转;
k取负整数时,顺时针方向旋转;k=0时,没有旋转.
(3)集合中的“k·360°”与“α”之间用“+”号连接,如k·360°-45°(k∈Z),应看作k·360°+(-45°) (k∈Z),表示与-45°角终边相同的角.
提示 相等的角终边一定相同,终边相同的角不一定相等.
知识拓展 象限角的集合表示
象限角 集合表示
第一象限角 {α|k·360°<α第二象限角 {α|k·360°+90°<α第三象限角 {α|k·360°+180°<α第四象限角 {α|k·360°+270°<α示例 在下列说法中:
①第一象限角一定不是负角;
②钝角都是第二象限角;
③与-30°角终边相同的角都是第四象限角;
④第二象限的角一定比第一象限的角大.
其中错误说法的序号为 .
解析 ①-350°角是第一象限角,但它是负角,错误.
②钝角的范围是大于90°且小于180°,显然是第二象限角,正确.
③因为-30°是第四象限角,所以与-30°角终边相同的角都是第四象限角,正确.
④象限角只能反映角的终边所在位置,不能反映角的大小.如376°是第一象限角,-190°是第二象限角,但376°>-190°,错误.
①④
示例 你能说出下列角是第几象限角吗?
131°;-76°.
解 在直角坐标系中,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,
画出这两角的终边如图所示,由图可知131°角为第二象限角,-76°角为第四象限角.
示例 写出终边落在直线y=x上的角的集合S,并把S中适合不等式-360°≤β<720°的元素β写出来.
解 直线y=x与x轴的夹角是45°,在0°~360°范围内,终边在直线y=x上的角有两个,即45°,225°.
因此,终边在直线y=x上的角的集合:
S={β|β=45°+k·360°,k∈Z}∪{β|β=225°+k·360°,k∈Z}
={β|β=45°+2k·180°,k∈Z}∪{β|β=45°+(2k+1)·180°,k∈Z}={β|β=45°+n·180°,n∈Z}.
∴ S中适合-360°≤β<720°的元素是
45°-2×180°=-315°;45°-1×180°=-135°;45°+0×180°=45°;45°+1×180°=225°;45°+2×180°=405°;45°+3×180°=585°.
归纳 终边落在各象限的角的集合可以借助如图所示的直角坐标系来记忆.
三 两个角终边对称或垂直的问题
角的终边是一条射线,在平面直角坐标系中,当两个角的终边具有对称性或互相垂直时,对应的角就有一定的关系.一般地,我们有如下结论.
角α,β终边的位置关系 α,β的关系
关于x轴对称 β=-α+k·360°(k∈Z)
关于y轴对称 β=-α+(2k+1)·180°(k∈Z)
关于原点对称 β=α+(2k+1)·180°(k∈Z)
关于直线y=x轴对称
关于直线y=-x轴对称
在一条直线上 β=α+k·180°(k∈Z)
垂直
知识拓展 轴线角的集合表示
角的终边位置 角的集合表示
终边落在x轴非负半轴上 {α|α=k·360°,k∈Z}
终边落在x轴非正半轴上 {α|α=k·360°+180°,k∈Z}
终边落在y轴非负半轴上 {α|α=k·360°+90°,k∈Z}或{α|α=k· 360°-270°,k∈Z}
终边落在y轴非正半轴上 {α|α=k·360°+270°,k∈Z}或{α|α=k·360°-90°,k∈Z}
终边落在x轴上 {α|α=k·180°,k∈Z}
终边落在y轴上 {α|α=k·180°+90°,k∈Z}
终边落在坐标轴上 {α|α=k·90°,k∈Z}
四 区间角、区域角
1区间角、区域角的定义
介于两个角之间的角的集合叫作区间角,如{x|60°2区域角的写法
(1)若角的终边落在一个区域内,写区域角时,先依逆时针方向由小到大写出一个区间角,再在它的两端分别加上“k·360°”,右端末注明“k∈Z”即可.
(2)若角的终边落在两个关于原点对称的区域内,写区域角时,可以先写出终边落在
其中一个区域内的一个区间角,再在此区间角的两端分别加上“k·180°”,右端末注明
“k∈Z”即可.例如,求终边落在图7-1-5阴影内(包括边界)的角的集合,可先求落在
第一象限内的一个区间角{α|45°≤α≤60°},则终边落在图中阴影内(包括边界)的角的
集合为{α|k·180°+45°≤α≤k·180°+60°,k∈Z}.
典例剖析
一、判断任意角所在象限
例 1 [多选题]在①160°,②480°,③-960°,④1 530°这四个角中,是第二象限角的是( )
A.① B.② C.③ D.④
【解析】第二象限角α需满足k·360°+90°<αABC
【方法总结】象限角的判断方法
(方法1)根据图象判定,在直角坐标系中作出角,角的终边落在第几象限,此角就是第几象限角.
(方法2)将角写成α=k·360°+β(0°≤β<360°,k∈Z)的形式,判断角β的终边所在的象限即可.
二、终边相同的角的表示及应用
1终边在某条射线上
例 2 终边在函数y=-x(x<0)的图象上的角β的集合S= .
【解析】函数y=-x(x<0)的图象是一条射线,且是第二象限的角平分线,则{β|β=135°+k·360°,k∈Z},所以终边在函数y=-x(x<0)的图象上的角β的集合S={β|β=135°+k·360°,k∈Z}.
{β|β=135°+k·360°,k∈Z}
【方法技巧】
先在0°~360°范围内,确定终边落在射线或直线上的特殊角,再推广到一般情况,最后写出终边相同的角的集合.
拓展:终边落在直线y=x上的角的集合为S={α|α=45°+k·180°,k∈Z},终边落在直线y=-x上的角的集合为S={α|α=-45°+k·180°,k∈Z}.
{α|α=60°+k·180°,k∈Z}
三、两个角的终边成对称问题
例 4 角α与角β的终边关于y轴对称,则α与β的关系为( )
A. α+β=k·360°,k∈Z B. α+β=k·360°+180°,k∈Z
C. α-β=k·360°+180°,k∈Z D. α-β=k·360°,k∈Z
【解析】(方法1:特殊值法)令α=30°,β=150°,则α+β=180°,
故α与β的关系为α+β=k·360°+180°,k∈Z.
(方法2:直接法)因为角α与角β的终边关于y轴对称,所以β=180°-α+k·360°,k∈Z,
即α+β=k·360°+180°,k∈Z.
B
【方法总结】
(1)若角α与β的终边关于x轴对称,则β=-α+k·360°,k∈Z.
(2)若角α与β的终边关于y轴对称,则β=180°-α+k·360°,k∈Z.
(3)若角α与β的终边关于原点对称,则β=180°+α+k·360°,k∈Z.
(4)若角α与β的终边关于直线y=x对称,则β=-α+90°+ k·360°,k∈Z.
四、任意角终边位置的确定和表示
例 5 在-360°到360°范围内,找出与下列各角终边相同的角,并判断它们是第几象限的角:
(1)-480°;(2)640°.
【解】(1)与-480°终边相同的角的集合为M={α|α=-480°+ k·360°,k∈Z}.
当k=1时,α=-480°+1×360°=-120°;当k=2时,α=-480°+2×360°=240°,
∴ 在-360°到360°范围内,与-480°终边相同的角是-120°和240°,都是第三象限的角.
(2)与640°终边相同的角的集合为N={β|β=640°+k· 360°,k∈Z}.
当k=-2时,β=640°-2×360°=-80°;当k=-1时,β=640°-1×360°=280°,
∴ 在-360°到360°范围内,与640°终边相同的角是-80°和280°,都是第四象限的角.
【方法总结】
在给定范围内找与给定角α终边相同的角的方法
(1)一般地,先写出与角α终边相同的角k·360°+α,k∈Z.
(2)根据所给范围,对k进行赋值,求出具体的角.
D
(1)
(2)
例 7 已知α是第三象限角,则-α是第( )象限角.
A.一 B.二 C.三 D.四
【解析】 ∵ α是第三象限角,∴ k·360°+180°<α∴ -k·360°-270°<-α<-k·360°-180°,k∈Z.∴ -α是第二象限角.
B
【方法技巧】
α与180°-α的终边关于y轴对称,类似地,α与-α的终边关于x轴对称,α与180°+α的终边关于原点对称,利用这些关系,可以由α的终边所在的象限直接看出相应角的终边所在的象限.
六、区间角的表示
1.阴影为一部分的区间的表示
例 8写出角的终边在图中阴影区域的角的集合(包括边界).
【解】先写出边界角,再按逆时针顺序写出区域角,
得{α|-150°+ k·360°≤α≤150°+k·360°,k∈Z}.
【解题步骤】表示区间角的三个步骤
(1)确定边界:按逆时针的方向找到区域的起始和终止边界;
(2)写出终边相同的角:先按由小到大分别标出起始和终止边界对应的0°~360°范围内的角,再写出终边落在起始和终止边界的所有角;
(3)写出区间角:按照逆时针方向,写出在起始边和终止边区间内的角的集合(或区间).
2.阴影为两部分的区间角的表示
例 9 如图所示,分别写出适合下列条件的角的集合:
(1)终边落在第一象限的阴影区域内;
(2)终边落在阴影区域内.
【解】 (1)终边落在射线OM上的角的集合为A={α|α=45°+k·360°,k∈Z},
终边落在射线ON上的角的集合为C={α|α=60°+k·360°,k∈Z},
故终边落在第一象限的阴影区域内的角的集合为D={α|45°+k· 360° ≤α<60°+k·360°,k∈Z}.
(2)终边落在射线OM反向延长线上的角的集合为B={α|α=225°+k· 360°,k∈Z},
则终边落在直线OM上的角的集合为
A∪B={α|α=45°+k·360°,k∈Z}∪{α|α=225°+ k·360°,k∈Z}
={α|α=45°+2k·180°,k∈Z}∪{α|α=45°+(2k+1)·180°,k∈Z}
={α|α=45°+n·180°,n∈Z}.
同理,终边落在直线ON上的角的集合为E={α|α=60°+n·180°,n∈Z},
则终边落在阴影区域内的角的集合为F={α|45°+n·180°≤α<60°+n·180°,n∈Z}.
1. 已知A={第一象限角},B={锐角},C={小于90°的角},则A,B,C关系正确的是( )
A. B=A∩C B. B∪C=C C. A?C D. A=B=C
2. 集合{α|k·180°≤α≤k·180°+45°,k∈Z}中角表示的范围(用阴影表示)是图中的( )
A B C D
3. 若α与β终边相同,则α-β的终边落在( )
A. x轴的非负半轴上 B. x轴的非正半轴上 C. y轴的非负半轴上 D. y轴的非正半轴上
4. 已知角2α的终边在x轴的上方,那么角α是( )
A.第一象限角 B.第一或第二象限角 C.第一或第三象限角 D.第一或第四象限角
5.给出下列四个结论:①-15°角是第四象限角;②185°角是第三象限角;③475°角是第二象限角;
④-350°角是第一象限角.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
B
随堂小测
B
A
C
D
ABD
谢 谢!
第7章
7.1
角与弧度
7.1.1 任意角
学习目标
1.理解任意角的概念,学会在平面内建立适当的坐标系来讨论任意角.
2.能在0°到360°范围内,找出一个与已知角终边相同的角,并判定其为第几象限角.
3.能写出与任一已知角终边相同的角的集合.
核心素养:数学抽象、数学运算、直观想象
新知学习
一 任意角的概念
1定义
一个角可以看作平面内一条射线绕着它的端点从
一个位置旋转到另一个位置所形成的图形.
射线的端点称为角的顶点,射线旋转的开始位置和终止位置称为角的始边和终边.
2角的表示
在不引起混淆的前提下,将“角α”或“∠α”简记作α.如图提示
在画图时,常用带箭头的弧来表示旋转的方向.
3角的分类
正角:按逆时针方向旋转所形成的角;
负角:按顺时针方向旋转所形成的角;
零角:一条射线没有作任何旋转.
角的概念推广到了任意角,包括正角、负角、零角.
提示
1.当角的始边和终边确定,但旋转的方向和旋转量的大小(旋转圈数)并没有确定时,角不能确定.
2.始边和终边重合的角不一定为零角,只有始边没有进行任何旋转,始边和终边重合的角才是零角.
示例[多选题]在下列说法中,说法错误的是( )
A.小于180°的角是钝角、直角或锐角
B.始边和终边重合的角是零角
C.钟表的时针旋转而成的角是负角
D.零角的始边和终边重合
解析 A.小于180°的角可能是钝角,直角或锐角,也可能是零角或负角,不正确;
B.始边和终边重合的角相差360°的整数倍,可能是零角,也可能不是零角,不正确;
C.钟表的时针是顺时针旋转而成的角,因而是负角,正确;
D.零角的始边未做任何旋转,因而和终边重合,正确.
AB
二 象限角、终边相同角
1定义
为了便于研究,以角的顶点为坐标原点,角的始边为x轴非负半轴,建立平面直角坐标系,这样,角的终边(除端点外)在第几象限,就说这个角是第几象限角.
如果角的终边在坐标轴上,这个角不属于任何象限,就说这个角为轴线角.
2与角α终边相同的角的集合
一般地,与α终边相同的角的集合为{β|β=k·360°+α,k∈Z}.
解读(1)α是任意角.
(2)“k∈Z”有三层含义:
①特殊性:每取一个整数值就对应一个具体的角.
②一般性:表示所有与角α终边相同的角(包括α自身).
③从几何意义上看,k表示角的终边按一定的方向旋转的圈数,k取正整数时,逆时针方向旋转;
k取负整数时,顺时针方向旋转;k=0时,没有旋转.
(3)集合中的“k·360°”与“α”之间用“+”号连接,如k·360°-45°(k∈Z),应看作k·360°+(-45°) (k∈Z),表示与-45°角终边相同的角.
提示 相等的角终边一定相同,终边相同的角不一定相等.
知识拓展 象限角的集合表示
象限角 集合表示
第一象限角 {α|k·360°<α
①第一象限角一定不是负角;
②钝角都是第二象限角;
③与-30°角终边相同的角都是第四象限角;
④第二象限的角一定比第一象限的角大.
其中错误说法的序号为 .
解析 ①-350°角是第一象限角,但它是负角,错误.
②钝角的范围是大于90°且小于180°,显然是第二象限角,正确.
③因为-30°是第四象限角,所以与-30°角终边相同的角都是第四象限角,正确.
④象限角只能反映角的终边所在位置,不能反映角的大小.如376°是第一象限角,-190°是第二象限角,但376°>-190°,错误.
①④
示例 你能说出下列角是第几象限角吗?
131°;-76°.
解 在直角坐标系中,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,
画出这两角的终边如图所示,由图可知131°角为第二象限角,-76°角为第四象限角.
示例 写出终边落在直线y=x上的角的集合S,并把S中适合不等式-360°≤β<720°的元素β写出来.
解 直线y=x与x轴的夹角是45°,在0°~360°范围内,终边在直线y=x上的角有两个,即45°,225°.
因此,终边在直线y=x上的角的集合:
S={β|β=45°+k·360°,k∈Z}∪{β|β=225°+k·360°,k∈Z}
={β|β=45°+2k·180°,k∈Z}∪{β|β=45°+(2k+1)·180°,k∈Z}={β|β=45°+n·180°,n∈Z}.
∴ S中适合-360°≤β<720°的元素是
45°-2×180°=-315°;45°-1×180°=-135°;45°+0×180°=45°;45°+1×180°=225°;45°+2×180°=405°;45°+3×180°=585°.
归纳 终边落在各象限的角的集合可以借助如图所示的直角坐标系来记忆.
三 两个角终边对称或垂直的问题
角的终边是一条射线,在平面直角坐标系中,当两个角的终边具有对称性或互相垂直时,对应的角就有一定的关系.一般地,我们有如下结论.
角α,β终边的位置关系 α,β的关系
关于x轴对称 β=-α+k·360°(k∈Z)
关于y轴对称 β=-α+(2k+1)·180°(k∈Z)
关于原点对称 β=α+(2k+1)·180°(k∈Z)
关于直线y=x轴对称
关于直线y=-x轴对称
在一条直线上 β=α+k·180°(k∈Z)
垂直
知识拓展 轴线角的集合表示
角的终边位置 角的集合表示
终边落在x轴非负半轴上 {α|α=k·360°,k∈Z}
终边落在x轴非正半轴上 {α|α=k·360°+180°,k∈Z}
终边落在y轴非负半轴上 {α|α=k·360°+90°,k∈Z}或{α|α=k· 360°-270°,k∈Z}
终边落在y轴非正半轴上 {α|α=k·360°+270°,k∈Z}或{α|α=k·360°-90°,k∈Z}
终边落在x轴上 {α|α=k·180°,k∈Z}
终边落在y轴上 {α|α=k·180°+90°,k∈Z}
终边落在坐标轴上 {α|α=k·90°,k∈Z}
四 区间角、区域角
1区间角、区域角的定义
介于两个角之间的角的集合叫作区间角,如{x|60°
(1)若角的终边落在一个区域内,写区域角时,先依逆时针方向由小到大写出一个区间角,再在它的两端分别加上“k·360°”,右端末注明“k∈Z”即可.
(2)若角的终边落在两个关于原点对称的区域内,写区域角时,可以先写出终边落在
其中一个区域内的一个区间角,再在此区间角的两端分别加上“k·180°”,右端末注明
“k∈Z”即可.例如,求终边落在图7-1-5阴影内(包括边界)的角的集合,可先求落在
第一象限内的一个区间角{α|45°≤α≤60°},则终边落在图中阴影内(包括边界)的角的
集合为{α|k·180°+45°≤α≤k·180°+60°,k∈Z}.
典例剖析
一、判断任意角所在象限
例 1 [多选题]在①160°,②480°,③-960°,④1 530°这四个角中,是第二象限角的是( )
A.① B.② C.③ D.④
【解析】第二象限角α需满足k·360°+90°<α
【方法总结】象限角的判断方法
(方法1)根据图象判定,在直角坐标系中作出角,角的终边落在第几象限,此角就是第几象限角.
(方法2)将角写成α=k·360°+β(0°≤β<360°,k∈Z)的形式,判断角β的终边所在的象限即可.
二、终边相同的角的表示及应用
1终边在某条射线上
例 2 终边在函数y=-x(x<0)的图象上的角β的集合S= .
【解析】函数y=-x(x<0)的图象是一条射线,且是第二象限的角平分线,则{β|β=135°+k·360°,k∈Z},所以终边在函数y=-x(x<0)的图象上的角β的集合S={β|β=135°+k·360°,k∈Z}.
{β|β=135°+k·360°,k∈Z}
【方法技巧】
先在0°~360°范围内,确定终边落在射线或直线上的特殊角,再推广到一般情况,最后写出终边相同的角的集合.
拓展:终边落在直线y=x上的角的集合为S={α|α=45°+k·180°,k∈Z},终边落在直线y=-x上的角的集合为S={α|α=-45°+k·180°,k∈Z}.
{α|α=60°+k·180°,k∈Z}
三、两个角的终边成对称问题
例 4 角α与角β的终边关于y轴对称,则α与β的关系为( )
A. α+β=k·360°,k∈Z B. α+β=k·360°+180°,k∈Z
C. α-β=k·360°+180°,k∈Z D. α-β=k·360°,k∈Z
【解析】(方法1:特殊值法)令α=30°,β=150°,则α+β=180°,
故α与β的关系为α+β=k·360°+180°,k∈Z.
(方法2:直接法)因为角α与角β的终边关于y轴对称,所以β=180°-α+k·360°,k∈Z,
即α+β=k·360°+180°,k∈Z.
B
【方法总结】
(1)若角α与β的终边关于x轴对称,则β=-α+k·360°,k∈Z.
(2)若角α与β的终边关于y轴对称,则β=180°-α+k·360°,k∈Z.
(3)若角α与β的终边关于原点对称,则β=180°+α+k·360°,k∈Z.
(4)若角α与β的终边关于直线y=x对称,则β=-α+90°+ k·360°,k∈Z.
四、任意角终边位置的确定和表示
例 5 在-360°到360°范围内,找出与下列各角终边相同的角,并判断它们是第几象限的角:
(1)-480°;(2)640°.
【解】(1)与-480°终边相同的角的集合为M={α|α=-480°+ k·360°,k∈Z}.
当k=1时,α=-480°+1×360°=-120°;当k=2时,α=-480°+2×360°=240°,
∴ 在-360°到360°范围内,与-480°终边相同的角是-120°和240°,都是第三象限的角.
(2)与640°终边相同的角的集合为N={β|β=640°+k· 360°,k∈Z}.
当k=-2时,β=640°-2×360°=-80°;当k=-1时,β=640°-1×360°=280°,
∴ 在-360°到360°范围内,与640°终边相同的角是-80°和280°,都是第四象限的角.
【方法总结】
在给定范围内找与给定角α终边相同的角的方法
(1)一般地,先写出与角α终边相同的角k·360°+α,k∈Z.
(2)根据所给范围,对k进行赋值,求出具体的角.
D
(1)
(2)
例 7 已知α是第三象限角,则-α是第( )象限角.
A.一 B.二 C.三 D.四
【解析】 ∵ α是第三象限角,∴ k·360°+180°<α
B
【方法技巧】
α与180°-α的终边关于y轴对称,类似地,α与-α的终边关于x轴对称,α与180°+α的终边关于原点对称,利用这些关系,可以由α的终边所在的象限直接看出相应角的终边所在的象限.
六、区间角的表示
1.阴影为一部分的区间的表示
例 8写出角的终边在图中阴影区域的角的集合(包括边界).
【解】先写出边界角,再按逆时针顺序写出区域角,
得{α|-150°+ k·360°≤α≤150°+k·360°,k∈Z}.
【解题步骤】表示区间角的三个步骤
(1)确定边界:按逆时针的方向找到区域的起始和终止边界;
(2)写出终边相同的角:先按由小到大分别标出起始和终止边界对应的0°~360°范围内的角,再写出终边落在起始和终止边界的所有角;
(3)写出区间角:按照逆时针方向,写出在起始边和终止边区间内的角的集合(或区间).
2.阴影为两部分的区间角的表示
例 9 如图所示,分别写出适合下列条件的角的集合:
(1)终边落在第一象限的阴影区域内;
(2)终边落在阴影区域内.
【解】 (1)终边落在射线OM上的角的集合为A={α|α=45°+k·360°,k∈Z},
终边落在射线ON上的角的集合为C={α|α=60°+k·360°,k∈Z},
故终边落在第一象限的阴影区域内的角的集合为D={α|45°+k· 360° ≤α<60°+k·360°,k∈Z}.
(2)终边落在射线OM反向延长线上的角的集合为B={α|α=225°+k· 360°,k∈Z},
则终边落在直线OM上的角的集合为
A∪B={α|α=45°+k·360°,k∈Z}∪{α|α=225°+ k·360°,k∈Z}
={α|α=45°+2k·180°,k∈Z}∪{α|α=45°+(2k+1)·180°,k∈Z}
={α|α=45°+n·180°,n∈Z}.
同理,终边落在直线ON上的角的集合为E={α|α=60°+n·180°,n∈Z},
则终边落在阴影区域内的角的集合为F={α|45°+n·180°≤α<60°+n·180°,n∈Z}.
1. 已知A={第一象限角},B={锐角},C={小于90°的角},则A,B,C关系正确的是( )
A. B=A∩C B. B∪C=C C. A?C D. A=B=C
2. 集合{α|k·180°≤α≤k·180°+45°,k∈Z}中角表示的范围(用阴影表示)是图中的( )
A B C D
3. 若α与β终边相同,则α-β的终边落在( )
A. x轴的非负半轴上 B. x轴的非正半轴上 C. y轴的非负半轴上 D. y轴的非正半轴上
4. 已知角2α的终边在x轴的上方,那么角α是( )
A.第一象限角 B.第一或第二象限角 C.第一或第三象限角 D.第一或第四象限角
5.给出下列四个结论:①-15°角是第四象限角;②185°角是第三象限角;③475°角是第二象限角;
④-350°角是第一象限角.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
B
随堂小测
B
A
C
D
ABD
谢 谢!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
