苏教版(2019)必修第一册6.3 对数函数课件(共41张PPT)
文档属性
| 名称 | 苏教版(2019)必修第一册6.3 对数函数课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览










文档简介
(共41张PPT)
第6章
6.3
对数函数
学习目标
1.通过实例直观了解对数函数模型所刻画的数量关系,理解对数函数的概念,体会对数函数是一类重要的数学模型.
2.能画出具体的对数函数的图象,探索并了解对数函数的性质.
3.能利用对数函数的性质比较两个对数式值的大小,能研究一些对数函数有关的复合函数的定义域、值域、单调性等.
4.知道指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数.
核心素养:数学抽象、直观想象、逻辑推理、数学运算
新知学习
一、对数函数的概念
一般地,函数y=logax(a>0,a≠1)叫作对数函数,其中x是自变量,定义域是(0,+∞).
【说明】(1)由指数式与对数式的关系,知对数函数的自变量x恰好是指数函数的函数值y,所以对数函数的定义域是(0,+∞).
(2)对数函数中底数的限制条件与指数函数中相同,为a>0,且a≠1.
(3)以10为底数的对数函数y=lg x叫作常用对数函数,以e为底数的对数函数y=ln x叫作自然对数函数.
二、对数函数的图象与性质
1.对数函数的图象与性质
一般地,对数函数y=logax(a>0,a≠1)的图象和性质如下表:
底数 a>1 0图象
性 质 定义域 (0,+∞)
值域 R
定点 函数图象恒过点(1,0),即当x=1时,y=0
函数值 的正负 当x>1时,y>0; 当01时,y<0;
当00
单调性 在(0,+∞)上为增函数 在(0,+∞)上为减函数
【说明】(1)对于对数函数的图象和性质,若底数a不确定,则需要分01两种情况讨论,这点与指数函数相同.
(2)对数函数的图象都在y轴右侧的第一、四象限,过定点(1,0),且当x→0时,图象无限接近y轴.
(3)对数函数的图象可以向上、向下无限延伸,值域为R.
【巧记】 对数函数单调性的记忆口诀
对数函数有两种,底数大小要分清.底数若是大于1,图象从左往右增.
底数0到1之间,图象从左往右减.无论函数增和减,图象都过(1,0)点.
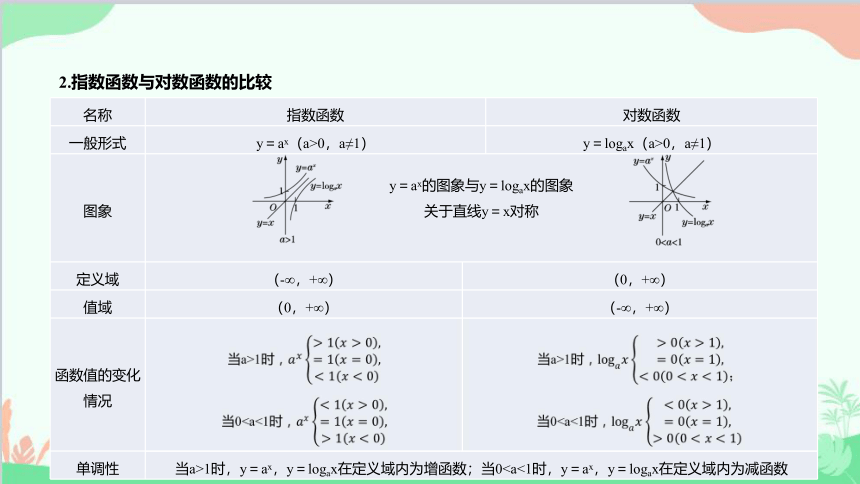
2.指数函数与对数函数的比较
名称 指数函数 对数函数
一般形式 y=ax(a>0,a≠1) y=logax(a>0,a≠1)
图象 y=ax的图象与y=logax的图象 关于直线y=x对称
定义域 (-∞,+∞) (0,+∞)
值域 (0,+∞) (-∞,+∞)
函数值的变化情况
单调性 当a>1时,y=ax,y=logax在定义域内为增函数;当0示例 函数y=log2x的定义域是[1,64),则值域是( )
A. R B.[0,+∞) C.[0,6) D.[0,64)
【规律总结】对数值正负的规律
(1)当a>1时,由对数函数y=logax是增函数知:若01,则logax>loga1=0.
(2)当0loga1=0;若x>1,则logax即对于区间(0,1)和(1,+∞),当a,x都在同一区间时,有logax>0;
当a,x分别在两个区间时,有logax<0.
可简记为:同区间为正,异区间为负.
C
【解析】 因为函数y=log2x在(0,+∞)上是增函数,所以当x∈[1,64)时,y∈[0,6).
3.底数的大小决定了对数函数图象的相对位置.
(1)上下比较:在直线x=1的右侧,当a>1时,a越大,对数函数图象越靠近x轴;当0(2)左右比较:比较对数函数图象与直线y=1交点横坐标的大小,交点的横坐标越大,对应的对数函数底数就越大.根据如图所示的图象,我们很容易验证此结论.
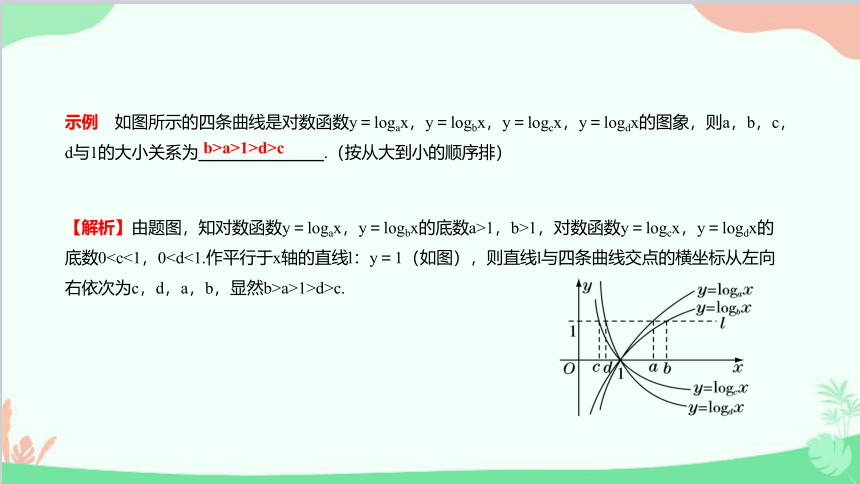
示例 如图所示的四条曲线是对数函数y=logax,y=logbx,y=logcx,y=logdx的图象,则a,b,c,d与1的大小关系为 .(按从大到小的顺序排)
b>a>1>d>c
【解析】由题图,知对数函数y=logax,y=logbx的底数a>1,b>1,对数函数y=logcx,y=logdx的底数0a>1>d>c.
四、反函数
1.反函数的定义
一般地,设A,B分别为函数y=f(x)的定义域和值域,如果由函数y=f(x)可解得唯一x=φ(y)也是一个函数(即对任意一个y∈B,都有唯一的x∈A与之对应),那么就称函数x=φ(y)是函数y=f(x)的反函数(inverse function),记作x=f -1(y).
根据指数式与对数式的互化,我们可以得到对数函数y=logax(a>0,且a≠1,x∈(0,+∞))与指数函数y=ax(a>0,且a≠1,x∈R)互为反函数.
2.反函数的性质
(1)互为反函数的两个函数的图象关于直线y=x对称.
若互为反函数的两个函数是同一个函数,则该函数的图象关于直线y=x对称.
(2)若函数y=f(x)图象上有一点(a,b),则(b,a)必在其反函数的图象上;反之,若点(b,a)在反函数的图象上,则(a,b)必在其原函数的图象上.
(3)反函数的定义域、值域分别是原函数的值域、定义域.
(4)互为反函数的两个函数的单调性相同.
示例 函数y=ln x+1(x>0)的反函数为( )
A. y=ex+1(x∈R) B. y=ex-1(x∈R) C. y=ex+1(x>1) D. y=ex-1(x>1)
【解题必备】求反函数的步骤
(1)求出函数y=f(x)的值域;(2)由y=f(x)解出x=f -1(y);
(3)把x=f -1(y)改写成y=f -1(x),并写出函数的定义域(原函数的值域).
B
【解析】 ∵ ln x=y-1,∴ x=ey-1.在原函数中,由x>0知y=ln x+ 1∈R.
故y=ln x+1(x>0)的反函数为y=ex-1(x∈R).
五、对数型复合函数的单调性
对数型复合函数一般分为两类:y=f(logax)型和y=logaf(x)型.
(1)对于对数型复合函数y=f(logax)(a>0,a≠1)的单调性,一般用复合法判定,即令t=logax,则只需研究t=logax及y=f(t)的单调性即可.
(2)对于对数型复合函数y=logaf(x)(a>0,a≠1)的单调性,首先由f(x)>0确定函数的定义域,然后判断t=f(x)在定义域上的单调性,最后结合底数a>1或0函数y=logat(a>0,a≠1)的单调性 函数y=logaf(x)(a>0,a≠1)的单调性
当a>1时, 函数y=logat在(0,+∞)上是增函数 当a>1时,若t=f(x)在(m,n)上是增函数,则y=logaf(x)在(m,n)上是增函数;
若t=f(x)在(p,q)上是减函数,则y=logaf(x)在(p,q)上是减函数
当0若t=f(x)在(p,q)上是减函数,则y=logaf(x)在(p,q)上是增函数
示例 求函数f(x)=log2(x2-2x)的单调区间.
【方法技巧】用换元法求复合函数的单调区间
求复合函数的单调区间的关键是分清内外两层函数,常采用换元法求解,忽略新元的取值范围是解题中的易错点.
【解】 函数f(x)的定义域为(-∞,0)∪(2,+∞).
设t=x2-2x.
当x∈(-∞,0)时,t=x2-2x为减函数,则f(x)在(-∞,0)上为减函数;
当x∈(2,+∞)时,t=x2-2x为增函数,则f(x)在(2,+∞)上为增函数.
典例剖析
D
A
【类题通法】对数(型)函数定义域的求法
1.求对数(型)函数的定义域时,除遵循前面求函数定义域的方法外,还要注意:
(1)真数大于0;(2)底数大于0且不等于1.
2.y=loga f(x)(a>0,且a≠1)型函数的定义域就是f(x)>0的解集.
3.y=f(logax)型函数的定义域保证f(x)的解析式有意义,保证真数大于0.
二、对数型函数的图象及应用
1.对数型函数图象过定点问题
例 2 函数y=loga(x+1)+1(a>0且a≠1)的图象恒过点( )
A.(0,1) B.(0,2) C.(-1,1) D.(-1,2)
A
【方法技巧】解答函数y=m+loga f(x)(a>0且a≠1)的图象恒过定点的问题时,只需令f(x)=1求出x,即得定点(x,m).
【解析】 要求函数y=loga(x+1)+1(a>0且a≠1)的图象恒过的点,只需令x+1=1,则x=0,y=1,所以该点的坐标为(0,1).
2.对数型函数图象的判定与识别
例 3 已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )
A B C D
【解析】(方法1)若0若a>1,则函数y=ax是增函数且过点(0,1),而函数y=loga(-x)是减函数且过点(-1,0),只有B中图象符合.
(方法2)首先指数函数y=ax的图象只可能在x轴上方区域,函数y=loga(-x)的图象只可能在y轴左侧区域,从而排除A,C;再看单调性,y=ax与y=loga(-x)的单调性正好相反,排除D.只有B中图象符合.
B
【方法技巧】给出函数解析式,判断函数的图象,首先应考虑所给函数对应的基本初等函数是哪一个,其次找出函数图象经过的特殊点,考虑函数的性质(定义域、单调性、奇偶性等),最后综合得出函数的图象.此类题目经常以选择题的形式出现,常用排除法.
3.对数型函数图象的变换
例 4 作出函数y=|log2(x+1)|+2的图象.
(1) (2) (3) (4)
【分析】充分利用图象变换,即利用平移变换、翻折变换等作图.
【解】第一步:作出y=log2x的图象(如图(1));
第二步:将y=log2x的图象沿x轴向左平移1个单位长度,得到y=log2(x+1)的图象(如图(2));
第三步:将y=log2(x+1)在x轴下方的图象以x轴为对称轴翻折到x轴的上方,得到y=|log2(x+1)|的图象(如图(3));
第四步:将y=|log2(x+1)|的图象沿y轴向上平移2个单位长度,得到y=|log2(x+1)|+2的图象(如图(4)).
【类题通法】函数图象的变换规律
(1)一般地,函数y=f(x+a)+b(a,b为实数)的图象是由函数y=f(x)的图象沿x轴向左或向右平移|a|个单位长度,再沿y轴向上或向下平移|b|个单位长度得到的.
(2)含有绝对值的函数的图象一般是经过对称变换得到的.一般地,y=f(|x-a|)的图象是关于直线x=a对称的轴对称图形;函数y=|f(x)|的图象与y=f(x)的图象在f(x)≥0的部分相同,在f(x)<0的部分关于x轴对称.
A
【规律方法】(1)指数函数y=ax与对数函数y=logax互为反函数.
(2)互为反函数的两个函数的定义域、值域相反.
(3)互为反函数的两个函数的图象关于直线y=x对称.
A
【解析】 由y=f(x)是y=ax的反函数,可知f(x)=logax(a>0,a≠1).
再由f(2)=1,可知loga2=1,所以a=2,即f(x)=log2x.
【类题通法】对数式比较大小的三种类型和求解方法
(1)底数相同时,利用对数函数单调性比较大小.
(2)底数与真数均不相同时,借助中间值0或1比较大小.
(3)真数相同时,可利用换底公式换成同底对数式,再比较大小,但要注意对数值的正负.
2.解对数不等式
例 8 (1)解不等式:loga(2x-5)>loga(x-1).
(2)已知log0.7(2x)
【类题通法】常见的对数不等式的三种类型及解法
(1)形如logax>logab的不等式,借助y=logax的单调性求解,如果a的取值不确定,那么需分a>1与0(2)形如logax>b的不等式,应将b化为以a为底数的对数式的形式,再借助y=logax的单调性求解;
(3)形如logax>logbx的不等式,可利用图象求解.
五、对数型复合函数问题
1.对数型复合函数的单调性问题
例 9 (1)函数f(x)=log2(x2+2x-3)的单调递增区间为( )
A.(-1,+∞) B.(1,+∞) C.(-∞,-1) D.(-∞,-3)
(2)已知函数f(x)=log2(3-ax)在[0,1]上是减函数,则a的取值范围是( )
A.(0,1) B.(1,3) C.(0,1)∪(1,3) D.(0,3)
D
B
【方法技巧】对数型复合函数的单调性的求解方法
对数型复合函数一般可分为两类:
一类是外层函数为对数函数,即y=loga f(x);另一类是内层函数为对数函数,即y=f(logax).
(1)对于y=loga f(x)型的函数的单调性,有以下结论:函数y=loga f(x)的单调性与函数u=f(x)(f(x)>0)的单调性在a>1时相同,在0(2)研究y=f(logax)型复合函数的单调性,一般用换元法,即令t=logax,则只需研究t=logax及y=
f(t)的单调性即可.
2.对数型复合函数的值域与最值
例10 已知函数f(x)=ln x+ln(a-x)的图象关于直线x=1对称,则函数f(x)的值域为( )
A.(0,2) B.[0,+∞) C.(-∞,2] D.(-∞,0]
【方法技巧】(1)求对数函数或与对数函数相关的复合函数的值域(最值)时,一般是根据单调性求解,若需要换元,则需考虑新元的取值范围.
(2)对于形如y=loga f(x)(a>0,a≠1)的复合函数,其值域的求解步骤如下:①求复合函数的定义域;②分解成y=logau,u=f(x)两个函数;③求u的取值范围;④利用y=logau的单调性求解即可.
D
【分析】 根据函数f(x)的图象关于直线x=1对称可得f(1+x)=f(1-x),由此可得a=2,即f(x)=ln x+ln(2-x),再结合函数的单调性和定义域求得值域.
【解析】∵ 函数f(x)=ln x+ln(a-x)的图象关于直线x=1对称,∴ f(1-x)=f(1+x),
即ln(1-x)+ln(a-1+x)=ln(1+x)+ln(a-1-x),∴ (1-x)(a-1+x)=(1+x)(a-1-x),
整理得(a-2)x=0,∴ a=2,∴ f(x)=ln x+ln(2-x),定义域为(0,2).
又f(x)=ln x+ln(2-x)=ln(2x-x2),当0∴ 函数f(x)的值域为(-∞,0].
3.对数型复合函数的奇偶性
例11 已知f(x)=loga(1+x),g(x)=loga(1- x)(a>0且a≠1).
(1)求函数y=f(x)-g(x)的定义域;
(2)判断函数y=f(x)-g(x)的奇偶性.
随堂小测
B
A
B
ACD
BC
ABC
log2x
lg x
10. 已知函数f(x),g(x)分别是定义在R上的奇函数和偶函数,且f(x)+g(x)=2x+1.
(1)求f(x),g(x)的解析式,并判断f(x)的单调性;
(2)已知m>0,且m≠1,不等式f(logm2)+f(-1)+2解:(1)由题可得f(-x)+g(-x)=2-x+1,则-f(x)+g(x)=2-x+1.又f(x)+g(x)=2x+1,
所以f(x)=2x-2-x,g(x)=2x+2-x.
因为y=2x在R上单调递增,y=2-x在R上单调递减,所以函数f(x)在R上单调递增.
(2)f(logm2)+f(-1)+2因为函数f(x)单调递增,所以logm2<1=logmm.
当0m,即0当m>1时,上式等价于22.
综上可知,m∈(0,1)∪(2,+∞).
11. 设函数f(x)=lg(ax-bx),其中a>0,b>0且a≠b.
(1)求f(x)的定义域;
(2)当a>1>b>0时,函数f(x)图象上是否存在不同两点,使过这两点的直线平行于x轴,并证明.
谢 谢!
第6章
6.3
对数函数
学习目标
1.通过实例直观了解对数函数模型所刻画的数量关系,理解对数函数的概念,体会对数函数是一类重要的数学模型.
2.能画出具体的对数函数的图象,探索并了解对数函数的性质.
3.能利用对数函数的性质比较两个对数式值的大小,能研究一些对数函数有关的复合函数的定义域、值域、单调性等.
4.知道指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数.
核心素养:数学抽象、直观想象、逻辑推理、数学运算
新知学习
一、对数函数的概念
一般地,函数y=logax(a>0,a≠1)叫作对数函数,其中x是自变量,定义域是(0,+∞).
【说明】(1)由指数式与对数式的关系,知对数函数的自变量x恰好是指数函数的函数值y,所以对数函数的定义域是(0,+∞).
(2)对数函数中底数的限制条件与指数函数中相同,为a>0,且a≠1.
(3)以10为底数的对数函数y=lg x叫作常用对数函数,以e为底数的对数函数y=ln x叫作自然对数函数.
二、对数函数的图象与性质
1.对数函数的图象与性质
一般地,对数函数y=logax(a>0,a≠1)的图象和性质如下表:
底数 a>1 0
性 质 定义域 (0,+∞)
值域 R
定点 函数图象恒过点(1,0),即当x=1时,y=0
函数值 的正负 当x>1时,y>0; 当0
当0
单调性 在(0,+∞)上为增函数 在(0,+∞)上为减函数
【说明】(1)对于对数函数的图象和性质,若底数a不确定,则需要分0
(2)对数函数的图象都在y轴右侧的第一、四象限,过定点(1,0),且当x→0时,图象无限接近y轴.
(3)对数函数的图象可以向上、向下无限延伸,值域为R.
【巧记】 对数函数单调性的记忆口诀
对数函数有两种,底数大小要分清.底数若是大于1,图象从左往右增.
底数0到1之间,图象从左往右减.无论函数增和减,图象都过(1,0)点.
2.指数函数与对数函数的比较
名称 指数函数 对数函数
一般形式 y=ax(a>0,a≠1) y=logax(a>0,a≠1)
图象 y=ax的图象与y=logax的图象 关于直线y=x对称
定义域 (-∞,+∞) (0,+∞)
值域 (0,+∞) (-∞,+∞)
函数值的变化情况
单调性 当a>1时,y=ax,y=logax在定义域内为增函数;当0
A. R B.[0,+∞) C.[0,6) D.[0,64)
【规律总结】对数值正负的规律
(1)当a>1时,由对数函数y=logax是增函数知:若0
(2)当0
当a,x分别在两个区间时,有logax<0.
可简记为:同区间为正,异区间为负.
C
【解析】 因为函数y=log2x在(0,+∞)上是增函数,所以当x∈[1,64)时,y∈[0,6).
3.底数的大小决定了对数函数图象的相对位置.
(1)上下比较:在直线x=1的右侧,当a>1时,a越大,对数函数图象越靠近x轴;当0
示例 如图所示的四条曲线是对数函数y=logax,y=logbx,y=logcx,y=logdx的图象,则a,b,c,d与1的大小关系为 .(按从大到小的顺序排)
b>a>1>d>c
【解析】由题图,知对数函数y=logax,y=logbx的底数a>1,b>1,对数函数y=logcx,y=logdx的底数0
四、反函数
1.反函数的定义
一般地,设A,B分别为函数y=f(x)的定义域和值域,如果由函数y=f(x)可解得唯一x=φ(y)也是一个函数(即对任意一个y∈B,都有唯一的x∈A与之对应),那么就称函数x=φ(y)是函数y=f(x)的反函数(inverse function),记作x=f -1(y).
根据指数式与对数式的互化,我们可以得到对数函数y=logax(a>0,且a≠1,x∈(0,+∞))与指数函数y=ax(a>0,且a≠1,x∈R)互为反函数.
2.反函数的性质
(1)互为反函数的两个函数的图象关于直线y=x对称.
若互为反函数的两个函数是同一个函数,则该函数的图象关于直线y=x对称.
(2)若函数y=f(x)图象上有一点(a,b),则(b,a)必在其反函数的图象上;反之,若点(b,a)在反函数的图象上,则(a,b)必在其原函数的图象上.
(3)反函数的定义域、值域分别是原函数的值域、定义域.
(4)互为反函数的两个函数的单调性相同.
示例 函数y=ln x+1(x>0)的反函数为( )
A. y=ex+1(x∈R) B. y=ex-1(x∈R) C. y=ex+1(x>1) D. y=ex-1(x>1)
【解题必备】求反函数的步骤
(1)求出函数y=f(x)的值域;(2)由y=f(x)解出x=f -1(y);
(3)把x=f -1(y)改写成y=f -1(x),并写出函数的定义域(原函数的值域).
B
【解析】 ∵ ln x=y-1,∴ x=ey-1.在原函数中,由x>0知y=ln x+ 1∈R.
故y=ln x+1(x>0)的反函数为y=ex-1(x∈R).
五、对数型复合函数的单调性
对数型复合函数一般分为两类:y=f(logax)型和y=logaf(x)型.
(1)对于对数型复合函数y=f(logax)(a>0,a≠1)的单调性,一般用复合法判定,即令t=logax,则只需研究t=logax及y=f(t)的单调性即可.
(2)对于对数型复合函数y=logaf(x)(a>0,a≠1)的单调性,首先由f(x)>0确定函数的定义域,然后判断t=f(x)在定义域上的单调性,最后结合底数a>1或0
当a>1时, 函数y=logat在(0,+∞)上是增函数 当a>1时,若t=f(x)在(m,n)上是增函数,则y=logaf(x)在(m,n)上是增函数;
若t=f(x)在(p,q)上是减函数,则y=logaf(x)在(p,q)上是减函数
当0
示例 求函数f(x)=log2(x2-2x)的单调区间.
【方法技巧】用换元法求复合函数的单调区间
求复合函数的单调区间的关键是分清内外两层函数,常采用换元法求解,忽略新元的取值范围是解题中的易错点.
【解】 函数f(x)的定义域为(-∞,0)∪(2,+∞).
设t=x2-2x.
当x∈(-∞,0)时,t=x2-2x为减函数,则f(x)在(-∞,0)上为减函数;
当x∈(2,+∞)时,t=x2-2x为增函数,则f(x)在(2,+∞)上为增函数.
典例剖析
D
A
【类题通法】对数(型)函数定义域的求法
1.求对数(型)函数的定义域时,除遵循前面求函数定义域的方法外,还要注意:
(1)真数大于0;(2)底数大于0且不等于1.
2.y=loga f(x)(a>0,且a≠1)型函数的定义域就是f(x)>0的解集.
3.y=f(logax)型函数的定义域保证f(x)的解析式有意义,保证真数大于0.
二、对数型函数的图象及应用
1.对数型函数图象过定点问题
例 2 函数y=loga(x+1)+1(a>0且a≠1)的图象恒过点( )
A.(0,1) B.(0,2) C.(-1,1) D.(-1,2)
A
【方法技巧】解答函数y=m+loga f(x)(a>0且a≠1)的图象恒过定点的问题时,只需令f(x)=1求出x,即得定点(x,m).
【解析】 要求函数y=loga(x+1)+1(a>0且a≠1)的图象恒过的点,只需令x+1=1,则x=0,y=1,所以该点的坐标为(0,1).
2.对数型函数图象的判定与识别
例 3 已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )
A B C D
【解析】(方法1)若0
(方法2)首先指数函数y=ax的图象只可能在x轴上方区域,函数y=loga(-x)的图象只可能在y轴左侧区域,从而排除A,C;再看单调性,y=ax与y=loga(-x)的单调性正好相反,排除D.只有B中图象符合.
B
【方法技巧】给出函数解析式,判断函数的图象,首先应考虑所给函数对应的基本初等函数是哪一个,其次找出函数图象经过的特殊点,考虑函数的性质(定义域、单调性、奇偶性等),最后综合得出函数的图象.此类题目经常以选择题的形式出现,常用排除法.
3.对数型函数图象的变换
例 4 作出函数y=|log2(x+1)|+2的图象.
(1) (2) (3) (4)
【分析】充分利用图象变换,即利用平移变换、翻折变换等作图.
【解】第一步:作出y=log2x的图象(如图(1));
第二步:将y=log2x的图象沿x轴向左平移1个单位长度,得到y=log2(x+1)的图象(如图(2));
第三步:将y=log2(x+1)在x轴下方的图象以x轴为对称轴翻折到x轴的上方,得到y=|log2(x+1)|的图象(如图(3));
第四步:将y=|log2(x+1)|的图象沿y轴向上平移2个单位长度,得到y=|log2(x+1)|+2的图象(如图(4)).
【类题通法】函数图象的变换规律
(1)一般地,函数y=f(x+a)+b(a,b为实数)的图象是由函数y=f(x)的图象沿x轴向左或向右平移|a|个单位长度,再沿y轴向上或向下平移|b|个单位长度得到的.
(2)含有绝对值的函数的图象一般是经过对称变换得到的.一般地,y=f(|x-a|)的图象是关于直线x=a对称的轴对称图形;函数y=|f(x)|的图象与y=f(x)的图象在f(x)≥0的部分相同,在f(x)<0的部分关于x轴对称.
A
【规律方法】(1)指数函数y=ax与对数函数y=logax互为反函数.
(2)互为反函数的两个函数的定义域、值域相反.
(3)互为反函数的两个函数的图象关于直线y=x对称.
A
【解析】 由y=f(x)是y=ax的反函数,可知f(x)=logax(a>0,a≠1).
再由f(2)=1,可知loga2=1,所以a=2,即f(x)=log2x.
【类题通法】对数式比较大小的三种类型和求解方法
(1)底数相同时,利用对数函数单调性比较大小.
(2)底数与真数均不相同时,借助中间值0或1比较大小.
(3)真数相同时,可利用换底公式换成同底对数式,再比较大小,但要注意对数值的正负.
2.解对数不等式
例 8 (1)解不等式:loga(2x-5)>loga(x-1).
(2)已知log0.7(2x)
【类题通法】常见的对数不等式的三种类型及解法
(1)形如logax>logab的不等式,借助y=logax的单调性求解,如果a的取值不确定,那么需分a>1与0
(3)形如logax>logbx的不等式,可利用图象求解.
五、对数型复合函数问题
1.对数型复合函数的单调性问题
例 9 (1)函数f(x)=log2(x2+2x-3)的单调递增区间为( )
A.(-1,+∞) B.(1,+∞) C.(-∞,-1) D.(-∞,-3)
(2)已知函数f(x)=log2(3-ax)在[0,1]上是减函数,则a的取值范围是( )
A.(0,1) B.(1,3) C.(0,1)∪(1,3) D.(0,3)
D
B
【方法技巧】对数型复合函数的单调性的求解方法
对数型复合函数一般可分为两类:
一类是外层函数为对数函数,即y=loga f(x);另一类是内层函数为对数函数,即y=f(logax).
(1)对于y=loga f(x)型的函数的单调性,有以下结论:函数y=loga f(x)的单调性与函数u=f(x)(f(x)>0)的单调性在a>1时相同,在0
f(t)的单调性即可.
2.对数型复合函数的值域与最值
例10 已知函数f(x)=ln x+ln(a-x)的图象关于直线x=1对称,则函数f(x)的值域为( )
A.(0,2) B.[0,+∞) C.(-∞,2] D.(-∞,0]
【方法技巧】(1)求对数函数或与对数函数相关的复合函数的值域(最值)时,一般是根据单调性求解,若需要换元,则需考虑新元的取值范围.
(2)对于形如y=loga f(x)(a>0,a≠1)的复合函数,其值域的求解步骤如下:①求复合函数的定义域;②分解成y=logau,u=f(x)两个函数;③求u的取值范围;④利用y=logau的单调性求解即可.
D
【分析】 根据函数f(x)的图象关于直线x=1对称可得f(1+x)=f(1-x),由此可得a=2,即f(x)=ln x+ln(2-x),再结合函数的单调性和定义域求得值域.
【解析】∵ 函数f(x)=ln x+ln(a-x)的图象关于直线x=1对称,∴ f(1-x)=f(1+x),
即ln(1-x)+ln(a-1+x)=ln(1+x)+ln(a-1-x),∴ (1-x)(a-1+x)=(1+x)(a-1-x),
整理得(a-2)x=0,∴ a=2,∴ f(x)=ln x+ln(2-x),定义域为(0,2).
又f(x)=ln x+ln(2-x)=ln(2x-x2),当0
3.对数型复合函数的奇偶性
例11 已知f(x)=loga(1+x),g(x)=loga(1- x)(a>0且a≠1).
(1)求函数y=f(x)-g(x)的定义域;
(2)判断函数y=f(x)-g(x)的奇偶性.
随堂小测
B
A
B
ACD
BC
ABC
log2x
lg x
10. 已知函数f(x),g(x)分别是定义在R上的奇函数和偶函数,且f(x)+g(x)=2x+1.
(1)求f(x),g(x)的解析式,并判断f(x)的单调性;
(2)已知m>0,且m≠1,不等式f(logm2)+f(-1)+2
所以f(x)=2x-2-x,g(x)=2x+2-x.
因为y=2x在R上单调递增,y=2-x在R上单调递减,所以函数f(x)在R上单调递增.
(2)f(logm2)+f(-1)+2
当0
综上可知,m∈(0,1)∪(2,+∞).
11. 设函数f(x)=lg(ax-bx),其中a>0,b>0且a≠b.
(1)求f(x)的定义域;
(2)当a>1>b>0时,函数f(x)图象上是否存在不同两点,使过这两点的直线平行于x轴,并证明.
谢 谢!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
