高中数学必修四上篇第3章章末复习课课件
文档属性
| 名称 | 高中数学必修四上篇第3章章末复习课课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 524.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-04 00:00:00 | ||
图片预览

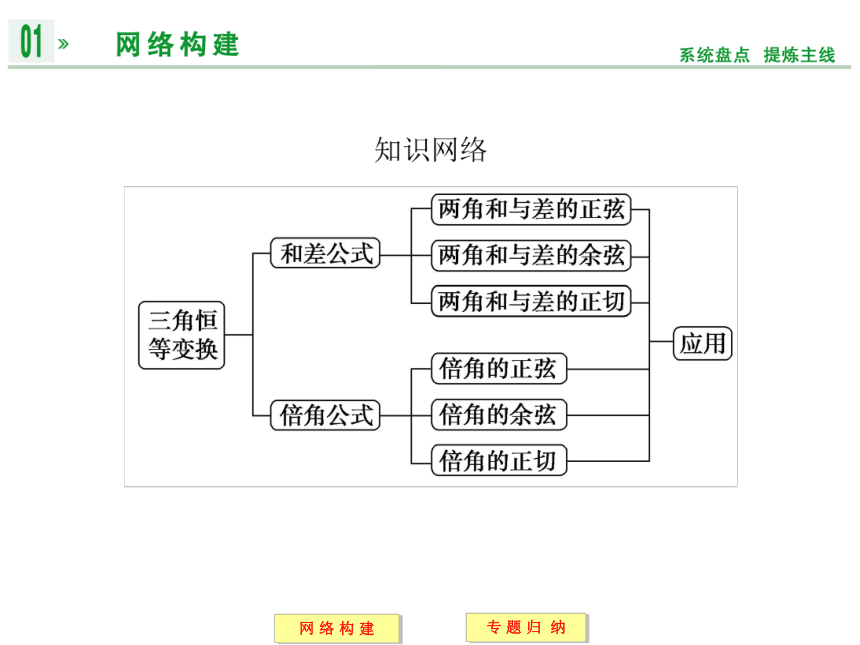







文档简介
课件26张PPT。章末复习课专题一 三角函数式的化简
三角函数式的化简,主要有以下几类:①对和式,基本思路是降幂、消项和逆用公式;②对分式,基本思路是分子与分母的约分和逆用公式,最终变成整式或数值;③对二次根式,则需要运用倍角公式的变形形式.在具体过程中体现的则是化归的思想,是一个“化异为同”的过程,涉及切弦互化,即“函数名”的“化同”;角的变换,即“单角化倍角”“单角化复角”“复角化复角”等具体手段.专题二 三角函数求值
三角函数求值主要有三种类型,即
(1)“给角求值”,一般给出的角都是非特殊角,观察发现题中的角与特殊角都有着一定的关系,如和或差为特殊角,必要时运用诱导公式.
(2)“给值求值”,即给出某些角的三角函数式的值,求另外一些三角函数的值,这类求值问题关键在于结合条件和结论中的角,合理拆、配角.要注意角的范围.
(3)“给值求角”,本质上还是“给值求值”,只不过往往求出的是特殊角的值,在求出角之前还需结合函数的单调性确定角,必要时还要讨论角的范围.专题四 三角函数与向量的综合应用
三角函数与向量的综合问题是近几年高考题的热点,目的在于考查学生对三角函数基本关系式的变形、运算和推理能力,一般来说题目难度不大,解决这类问题,应利用平面向量的坐标、数量积、平行与垂直的条件、夹角公式等知识将向量转化为三角函数问题.(1)证明 法一 ∵a=(cos α,sin α),b=(cos β,sin β),
∴a+b=(cos α+cos β,sin α+sin β),
a-b=(cos α-cos β,sin α-sin β),
∴(a+b)·(a-b)
=(cos α+cos β)(cos α-cos β)+(sin α+sin β)(sin α-sin β)
=cos2α-cos2β+sin2α-sin2β=0.
∴(a+b)⊥(a-b).
法二 ∵a=(cos α,sin α),b=(cos β,sin β),
∴|a|2=cos2α+sin2α=1,|b|2=cos2β+sin2β=1.
∴|a|2=|b|2.
∴(a+b)(a-b)=a2-b2=|a|2-|b|2=0,
∴(a+b)⊥(a-b).
(2)解 ∵ka+b=(kcos α,ksin α)+(cos β,sin β)
=(kcos α+cos β,ksin α+sin β),
a-kb=(cos α-kcos β,sin α-ksin β),
∴|ka+b|2=(kcos α+cos β)2+(ksin α+sin β)2
专题五 三角恒等变换与三角函数的综合问题
利用三角公式和基本的三角恒等变换的思想方法,可以化简三角函数的解析式,进而才能顺利地探求三角函数的有关性质.反过来,利用三角函数性质,可确定解析式,进而可求出有关三角函数值.因而三角恒等变换与三角函数的综合问题是高考命题的热点.
解决三角恒等变换与三角函数的综合问题关键在于熟练地运用基本的三角恒等变换思想方法,对其解析式变形、化简,尽量使其化为只有一个角为自变量的三角函数.解决与图象和性质有关的问题,在进行恒等变换时,既要注意三角恒等思想(切割化弦、常值代换、降幂与升幂、收缩代换、和差与积的互化,角的代换)的运用;还要注意一般的数学思想方法(如换元法等)的运用.
三角函数式的化简,主要有以下几类:①对和式,基本思路是降幂、消项和逆用公式;②对分式,基本思路是分子与分母的约分和逆用公式,最终变成整式或数值;③对二次根式,则需要运用倍角公式的变形形式.在具体过程中体现的则是化归的思想,是一个“化异为同”的过程,涉及切弦互化,即“函数名”的“化同”;角的变换,即“单角化倍角”“单角化复角”“复角化复角”等具体手段.专题二 三角函数求值
三角函数求值主要有三种类型,即
(1)“给角求值”,一般给出的角都是非特殊角,观察发现题中的角与特殊角都有着一定的关系,如和或差为特殊角,必要时运用诱导公式.
(2)“给值求值”,即给出某些角的三角函数式的值,求另外一些三角函数的值,这类求值问题关键在于结合条件和结论中的角,合理拆、配角.要注意角的范围.
(3)“给值求角”,本质上还是“给值求值”,只不过往往求出的是特殊角的值,在求出角之前还需结合函数的单调性确定角,必要时还要讨论角的范围.专题四 三角函数与向量的综合应用
三角函数与向量的综合问题是近几年高考题的热点,目的在于考查学生对三角函数基本关系式的变形、运算和推理能力,一般来说题目难度不大,解决这类问题,应利用平面向量的坐标、数量积、平行与垂直的条件、夹角公式等知识将向量转化为三角函数问题.(1)证明 法一 ∵a=(cos α,sin α),b=(cos β,sin β),
∴a+b=(cos α+cos β,sin α+sin β),
a-b=(cos α-cos β,sin α-sin β),
∴(a+b)·(a-b)
=(cos α+cos β)(cos α-cos β)+(sin α+sin β)(sin α-sin β)
=cos2α-cos2β+sin2α-sin2β=0.
∴(a+b)⊥(a-b).
法二 ∵a=(cos α,sin α),b=(cos β,sin β),
∴|a|2=cos2α+sin2α=1,|b|2=cos2β+sin2β=1.
∴|a|2=|b|2.
∴(a+b)(a-b)=a2-b2=|a|2-|b|2=0,
∴(a+b)⊥(a-b).
(2)解 ∵ka+b=(kcos α,ksin α)+(cos β,sin β)
=(kcos α+cos β,ksin α+sin β),
a-kb=(cos α-kcos β,sin α-ksin β),
∴|ka+b|2=(kcos α+cos β)2+(ksin α+sin β)2
专题五 三角恒等变换与三角函数的综合问题
利用三角公式和基本的三角恒等变换的思想方法,可以化简三角函数的解析式,进而才能顺利地探求三角函数的有关性质.反过来,利用三角函数性质,可确定解析式,进而可求出有关三角函数值.因而三角恒等变换与三角函数的综合问题是高考命题的热点.
解决三角恒等变换与三角函数的综合问题关键在于熟练地运用基本的三角恒等变换思想方法,对其解析式变形、化简,尽量使其化为只有一个角为自变量的三角函数.解决与图象和性质有关的问题,在进行恒等变换时,既要注意三角恒等思想(切割化弦、常值代换、降幂与升幂、收缩代换、和差与积的互化,角的代换)的运用;还要注意一般的数学思想方法(如换元法等)的运用.
