北师大版数学七年级上册 第三章 整式及其加减第8课时探索与表达规律 课件(共30张PPT)
文档属性
| 名称 | 北师大版数学七年级上册 第三章 整式及其加减第8课时探索与表达规律 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 604.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 13:00:15 | ||
图片预览










文档简介
(共30张PPT)
第三章 整式及其加减
第8课时 探索与表达规律
目录
01
温故知新
03
课堂导练
02
探究新知
温故知新
1. 下列运算正确的是( )
A. 3x-2x=1 B. 2a+3b=5ab
C. 2ab+ab=3ab D. 2(x+1)=2x+1
C
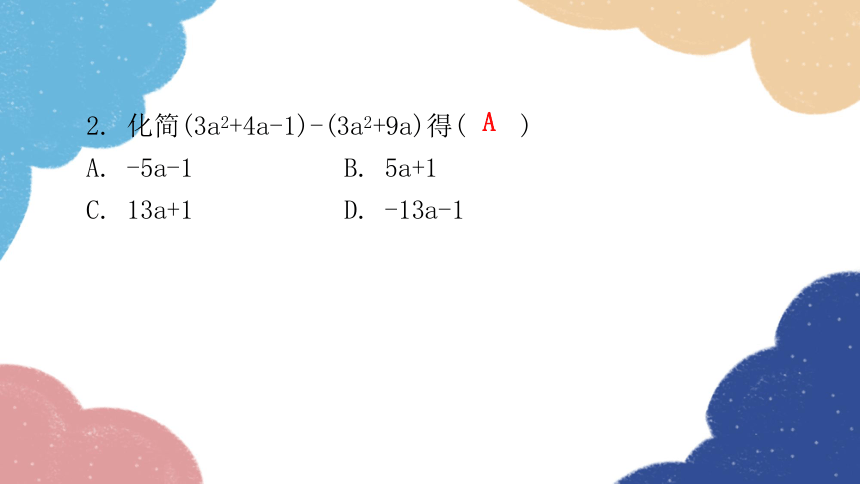
2. 化简(3a2+4a-1)-(3a2+9a)得( )
A. -5a-1 B. 5a+1
C. 13a+1 D. -13a-1
A
探究新知
(1)若各项为整数,考虑相邻两数的和、差、积、商、符号等方面是否存在规律,也可以是存在奇、偶、平方等方面的规律;
(2)若各项为分数,可分别观察分子、分母的变化规律及它们之间的联系;
(3)若为表格的形式,可以比较每一行每一列数字之间的关系,从而找出规律.
知识点一
用代数式表示数式变化中的规律
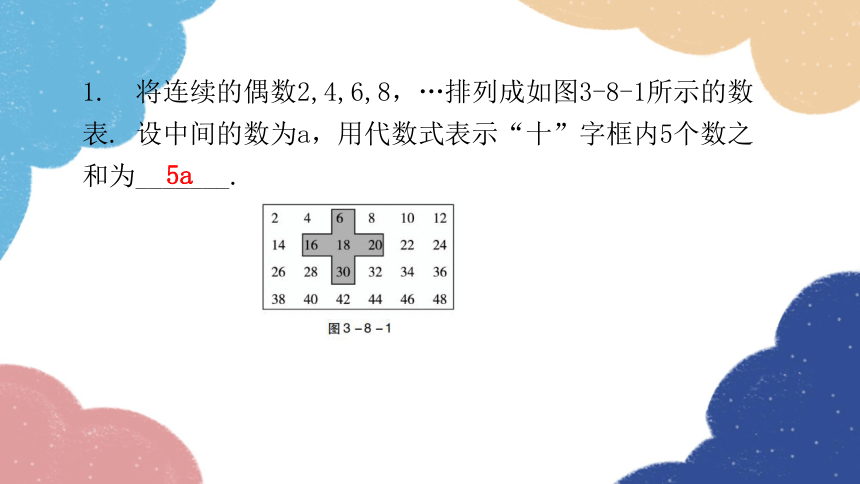
1. 将连续的偶数2,4,6,8,…排列成如图3-8-1所示的数表. 设中间的数为a,用代数式表示“十”字框内5个数之和为_______.
5a
(1)观察图形的结构特点,归纳相对于某个基本图形的递推规律,从而将图形转化为一列数或式子,继而探究规律;(2)将图形所研究的量转化为一列数,由这一列数去寻找规律.
知识点二
用代数式表示图形变化中的规律
2. 用同样大小的黑色棋子按如图3-8-2的方式摆图形,按照这样的规律摆下去,则第n个图形需___________枚棋子.(用含n的代数式表示)
(3n+1)
课堂导练
【例1】观察一串数:0,2,4,6,…,则第n个数
是( )
A. 2(n-1) B. 2n-1
C. 2(n+1) D. 2n+1
思路点拨:观察分析数据,寻找它们之间的相互联系.
A
【例2】将连续的奇数1,3,5,7,9,…,排成如图3-8-3的数阵.
(1)十字框中的五个数的和与中间数15有什么关系;(2)设中间数为a,用式子表示十字框中五个数之和;
(3)十字框中五个数之和能等于2 015吗?
若能,请写出这五个数;若不能,
说明理由;
(4)十字框中五个数之和能等于2 020吗?
若能,请写出这五个数;若不能,
说明理由.
解:(1)因为5+13+15+17+25=75=5×15,所以十字框中的五个数的和是中间数15的5倍.
(2)由(1)知,若中间数为a,则其它4个数分别为a-10,a-2,a+2,a+10,
则十字框中五个数之和为a-10+(a-2)+a+(a+2)+(a+10)=5a.
(3)十字框中五个数的和能等于2 015. 理由如下:
设十字框中间的数为x.
由(2)知,5个数之和为5x=2 015.
解得x=403.
因为403为奇数,且在数阵的第40行第二列,所以存在五个数之和等于2 015,这五个数分别为393,401,403,405,413.
(4)十字框中五个数的和不能等于2 020.理由如下:设十字框中间的数为y.由(2)知,5个数之和为5y=2 020.解得y=404.因为404为偶数,不在此数阵中,故不能.
思路点拨:(1)将十字框中的五个数相加即可得出结论;(2)结合(1)将15替换成a,则可得出结论;(3) (4)结合(2)中的式子,分别求出当和为2 015和2 020时中间数的值,再根据数阵的特点判断即可得出结论.
2. 如图3-8-4,表②,表③分别是从表①中选取的一部分,表①中的第一行的第四个数是3,第二行的第三个数是5,根据表①中的规律,回答下列问题:
表①
0 1 2 3 ...
1 3 5 7 ...
2 5 8 11 ...
3 7 11 15 ...
... ... ... ... ...
表② 表③
11
14
a
11 13
17 b
(1)表①中的第四行第五个数是_______;
(2)表②表③中的a与b 的和是_______;
(3)表①中的第n行第7个数是_______;(用含n的代数式表示)
(4)表①中的第10行第m个数是_______. (用含有m的代数式表示)
19
37
7n-1
10m-1
【例3】(1)按图3-8-5①方式摆放餐桌和椅子,照这样的方式继续排列餐桌,摆4张桌子可坐多少人?摆5张桌子呢?摆n张桌子呢?
(2)按图3-8-5②方式摆放餐桌和椅子,照这样的方式继续排列餐桌,摆4张桌子可坐多少人?摆5张桌子呢?摆n张桌子呢?
解:(1)由图可知摆1张餐桌上可以坐6人,
摆2张餐桌上可以坐8人,
摆3张餐桌上可以坐10人,
…
所以摆n张餐桌共可以坐6+2(n-1)=(2n+4)人.
所以摆4张桌子可坐2×4+4=12(人),
摆5张桌子2×5+4=14(人).
(2)由图可知摆1张餐桌上可以坐6人,
摆2张餐桌上可以坐10人,
摆3张餐桌上可以坐14人,
…
所以摆n张餐桌共可以坐6+4(n-1)=(4n+2)人.
所以摆4张桌子可坐4×4+2=18(人),
摆5张桌子4×5+2=22(人).
思路点拨:根据图中桌椅的摆放形式找到变化的规律,再根据变化的规律得出答案即可.
3. 用同样规格的黑白两种颜色的正方形. 按如图3-8-6的方式拼图,请根据图中的信息完成下列的问题:
(1)在图②中用了____块白色正方形,在图③中用了____块白色正方形;
8
11
(2)按图中的规律继续铺下去,求第n个图形要用多少块白色正方形;
(3)如果有足够多的黑色正方形,能不能恰好用完2 021块白色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
解:(2)在图①中,需要白色正方形的块数为3×1+2=5(块);
在图②中,需要白色正方形的块数为3×2+2=8(块);
在图③中,需要白色正方形的块数为3×3+2=11(块);
由此可以发现,第几个图形,需要白色正方形的块数就等于3乘以几,然后加2.
所以按图中的规律继续铺下去,那么第n个图形要用(3n+2)块白色正方形.
(3)能恰好用完2 021块白色正方形.
理由如下:
设第n个图形恰好能用完2 021块白色正方形,则3n+2=2 021.
解得n=673.
所以第673个图形中恰好能用完2 021块白色正方形.
【例4】用火柴棒按如图3-8-7的方式搭图形.
(1)按图示规律完成下表:
图形标号 ① ② ③ ④ ⑤ …
火柴棒根数 5 9 ______ ______ ______ ...
13
17
21
(2)按照这种方式搭下去,搭第n个图形需要多少根火柴棒?(3)搭第2 022个图形需要多少根火柴棒?
解:(2)由(1)得,搭第n个图形需要火柴棒5+4(n-1)=(4n+1)根. 所以第n个图形需要火柴棒(4n+1)根.
(3)由(2)得,当n=2 022时,4n+1=4×2 022+1=8 089,所以搭第2 022个图形需要8 089根火柴棒.
思路点拨:(1)根据所给的图形进行分析即可得出结果;(2)由(1)进行总结即可;(3)根据(2)所得的式子进行解答即可.
4. 如图3-8-8是由一些火柴棒摆成的图案:
(1)摆第1个图案用6根火柴棒,摆第2个图案用11根火柴棒,摆第3个图案用____根火柴棒;
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒 (n为正整数)
(3)用1 001根火柴棒能摆成第几个图案?
16
解:(2)第1个图案的火柴数为6根,
第2个图案的火柴数为6+5×1=11(根),
第3个图案的火柴数为6+5×2=16(根),
…
所以第n个图案的火柴数为6+5(n-1)=(5n+1)根.
(3)由(2)得,5n+1=1 001.
解得n=200.
所以用1 001根火柴棒能摆成第200个图案.
【例5】(教材创新题)杨辉是我国南宋时期杰出的数学家和教育家,如图3-8-9是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,它是古代重要的数学成就,比西方的“帕斯卡三角形”早了300多年,请仔细观察,计算图中第n行中所有数字之和为_________.
思路点拨:此题考查数字
的变化规律,注意结合数的
排列形状,找出规律解决问题.
2n-1
5. (创新变式)观察下列等式:
第1层1+2=3,
第2层4+5+6=7+8,
第3层9+10+11+12=13+14+15,
第4层16+17+18+19+20=21+22+23+24,
…
在上述数字宝塔中,从上往下数,2 022所在的层数是( )
A. 第33层 B. 第34层
C. 第44层 D. 第45层
C
谢 谢
第三章 整式及其加减
第8课时 探索与表达规律
目录
01
温故知新
03
课堂导练
02
探究新知
温故知新
1. 下列运算正确的是( )
A. 3x-2x=1 B. 2a+3b=5ab
C. 2ab+ab=3ab D. 2(x+1)=2x+1
C
2. 化简(3a2+4a-1)-(3a2+9a)得( )
A. -5a-1 B. 5a+1
C. 13a+1 D. -13a-1
A
探究新知
(1)若各项为整数,考虑相邻两数的和、差、积、商、符号等方面是否存在规律,也可以是存在奇、偶、平方等方面的规律;
(2)若各项为分数,可分别观察分子、分母的变化规律及它们之间的联系;
(3)若为表格的形式,可以比较每一行每一列数字之间的关系,从而找出规律.
知识点一
用代数式表示数式变化中的规律
1. 将连续的偶数2,4,6,8,…排列成如图3-8-1所示的数表. 设中间的数为a,用代数式表示“十”字框内5个数之和为_______.
5a
(1)观察图形的结构特点,归纳相对于某个基本图形的递推规律,从而将图形转化为一列数或式子,继而探究规律;(2)将图形所研究的量转化为一列数,由这一列数去寻找规律.
知识点二
用代数式表示图形变化中的规律
2. 用同样大小的黑色棋子按如图3-8-2的方式摆图形,按照这样的规律摆下去,则第n个图形需___________枚棋子.(用含n的代数式表示)
(3n+1)
课堂导练
【例1】观察一串数:0,2,4,6,…,则第n个数
是( )
A. 2(n-1) B. 2n-1
C. 2(n+1) D. 2n+1
思路点拨:观察分析数据,寻找它们之间的相互联系.
A
【例2】将连续的奇数1,3,5,7,9,…,排成如图3-8-3的数阵.
(1)十字框中的五个数的和与中间数15有什么关系;(2)设中间数为a,用式子表示十字框中五个数之和;
(3)十字框中五个数之和能等于2 015吗?
若能,请写出这五个数;若不能,
说明理由;
(4)十字框中五个数之和能等于2 020吗?
若能,请写出这五个数;若不能,
说明理由.
解:(1)因为5+13+15+17+25=75=5×15,所以十字框中的五个数的和是中间数15的5倍.
(2)由(1)知,若中间数为a,则其它4个数分别为a-10,a-2,a+2,a+10,
则十字框中五个数之和为a-10+(a-2)+a+(a+2)+(a+10)=5a.
(3)十字框中五个数的和能等于2 015. 理由如下:
设十字框中间的数为x.
由(2)知,5个数之和为5x=2 015.
解得x=403.
因为403为奇数,且在数阵的第40行第二列,所以存在五个数之和等于2 015,这五个数分别为393,401,403,405,413.
(4)十字框中五个数的和不能等于2 020.理由如下:设十字框中间的数为y.由(2)知,5个数之和为5y=2 020.解得y=404.因为404为偶数,不在此数阵中,故不能.
思路点拨:(1)将十字框中的五个数相加即可得出结论;(2)结合(1)将15替换成a,则可得出结论;(3) (4)结合(2)中的式子,分别求出当和为2 015和2 020时中间数的值,再根据数阵的特点判断即可得出结论.
2. 如图3-8-4,表②,表③分别是从表①中选取的一部分,表①中的第一行的第四个数是3,第二行的第三个数是5,根据表①中的规律,回答下列问题:
表①
0 1 2 3 ...
1 3 5 7 ...
2 5 8 11 ...
3 7 11 15 ...
... ... ... ... ...
表② 表③
11
14
a
11 13
17 b
(1)表①中的第四行第五个数是_______;
(2)表②表③中的a与b 的和是_______;
(3)表①中的第n行第7个数是_______;(用含n的代数式表示)
(4)表①中的第10行第m个数是_______. (用含有m的代数式表示)
19
37
7n-1
10m-1
【例3】(1)按图3-8-5①方式摆放餐桌和椅子,照这样的方式继续排列餐桌,摆4张桌子可坐多少人?摆5张桌子呢?摆n张桌子呢?
(2)按图3-8-5②方式摆放餐桌和椅子,照这样的方式继续排列餐桌,摆4张桌子可坐多少人?摆5张桌子呢?摆n张桌子呢?
解:(1)由图可知摆1张餐桌上可以坐6人,
摆2张餐桌上可以坐8人,
摆3张餐桌上可以坐10人,
…
所以摆n张餐桌共可以坐6+2(n-1)=(2n+4)人.
所以摆4张桌子可坐2×4+4=12(人),
摆5张桌子2×5+4=14(人).
(2)由图可知摆1张餐桌上可以坐6人,
摆2张餐桌上可以坐10人,
摆3张餐桌上可以坐14人,
…
所以摆n张餐桌共可以坐6+4(n-1)=(4n+2)人.
所以摆4张桌子可坐4×4+2=18(人),
摆5张桌子4×5+2=22(人).
思路点拨:根据图中桌椅的摆放形式找到变化的规律,再根据变化的规律得出答案即可.
3. 用同样规格的黑白两种颜色的正方形. 按如图3-8-6的方式拼图,请根据图中的信息完成下列的问题:
(1)在图②中用了____块白色正方形,在图③中用了____块白色正方形;
8
11
(2)按图中的规律继续铺下去,求第n个图形要用多少块白色正方形;
(3)如果有足够多的黑色正方形,能不能恰好用完2 021块白色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
解:(2)在图①中,需要白色正方形的块数为3×1+2=5(块);
在图②中,需要白色正方形的块数为3×2+2=8(块);
在图③中,需要白色正方形的块数为3×3+2=11(块);
由此可以发现,第几个图形,需要白色正方形的块数就等于3乘以几,然后加2.
所以按图中的规律继续铺下去,那么第n个图形要用(3n+2)块白色正方形.
(3)能恰好用完2 021块白色正方形.
理由如下:
设第n个图形恰好能用完2 021块白色正方形,则3n+2=2 021.
解得n=673.
所以第673个图形中恰好能用完2 021块白色正方形.
【例4】用火柴棒按如图3-8-7的方式搭图形.
(1)按图示规律完成下表:
图形标号 ① ② ③ ④ ⑤ …
火柴棒根数 5 9 ______ ______ ______ ...
13
17
21
(2)按照这种方式搭下去,搭第n个图形需要多少根火柴棒?(3)搭第2 022个图形需要多少根火柴棒?
解:(2)由(1)得,搭第n个图形需要火柴棒5+4(n-1)=(4n+1)根. 所以第n个图形需要火柴棒(4n+1)根.
(3)由(2)得,当n=2 022时,4n+1=4×2 022+1=8 089,所以搭第2 022个图形需要8 089根火柴棒.
思路点拨:(1)根据所给的图形进行分析即可得出结果;(2)由(1)进行总结即可;(3)根据(2)所得的式子进行解答即可.
4. 如图3-8-8是由一些火柴棒摆成的图案:
(1)摆第1个图案用6根火柴棒,摆第2个图案用11根火柴棒,摆第3个图案用____根火柴棒;
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒 (n为正整数)
(3)用1 001根火柴棒能摆成第几个图案?
16
解:(2)第1个图案的火柴数为6根,
第2个图案的火柴数为6+5×1=11(根),
第3个图案的火柴数为6+5×2=16(根),
…
所以第n个图案的火柴数为6+5(n-1)=(5n+1)根.
(3)由(2)得,5n+1=1 001.
解得n=200.
所以用1 001根火柴棒能摆成第200个图案.
【例5】(教材创新题)杨辉是我国南宋时期杰出的数学家和教育家,如图3-8-9是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,它是古代重要的数学成就,比西方的“帕斯卡三角形”早了300多年,请仔细观察,计算图中第n行中所有数字之和为_________.
思路点拨:此题考查数字
的变化规律,注意结合数的
排列形状,找出规律解决问题.
2n-1
5. (创新变式)观察下列等式:
第1层1+2=3,
第2层4+5+6=7+8,
第3层9+10+11+12=13+14+15,
第4层16+17+18+19+20=21+22+23+24,
…
在上述数字宝塔中,从上往下数,2 022所在的层数是( )
A. 第33层 B. 第34层
C. 第44层 D. 第45层
C
谢 谢
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
