2.2.1基本不等式 课件(共22张PPT)

(共22张PPT)
2.2.1 基本不等式
人教A版（2019）必修一
教学目标
1.学会推导并掌握基本不等式，能够对其进行证明，并探索其几何意义；
2.能够运用基本不等式来求代数式的最值，提高数学抽象和逻辑推理核心素养；
3.通过探索基本不等式的推导过程，帮助学生领会数形结合的数学思想，并提高逻辑推理和直观想象的核心素养水平。
如图，这是2002年在北京召开的第24届国际数学家大会会标．颜色的明暗使它看上去象一个风车，代表中国人民热情好客。
古代数学家 赵爽
勾股弦图
a
b
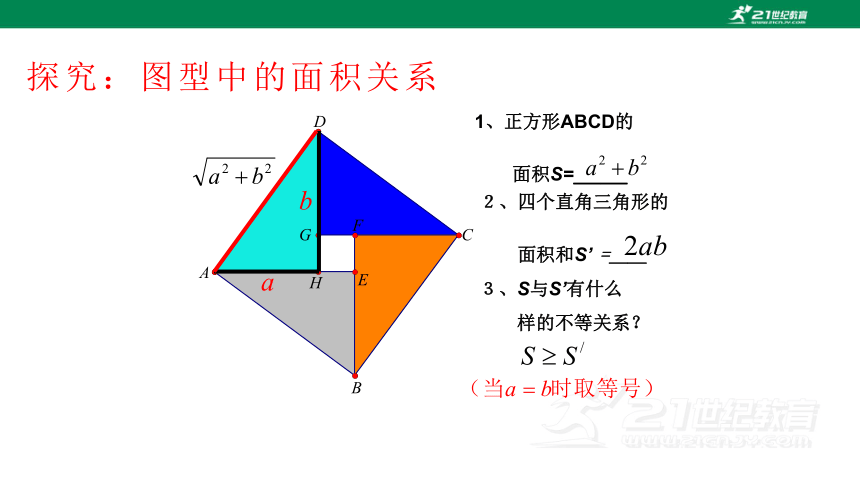
1、正方形ABCD的
　　面积S=＿＿
２、四个直角三角形的
　　面积和S’ =＿＿
３、S与S’有什么　　　
　　样的不等关系？
当且仅当a=b时，等号成立。
基本不等式（均值不等式）：
均值定理:两个正数的算术平均数不小于它们的几何平均数
几何平均数
算术平均数
法一：
探索基本不等式的证明
（比较法）
若a∈R,b∈R
（当且仅当a=b时，
取“=”号）
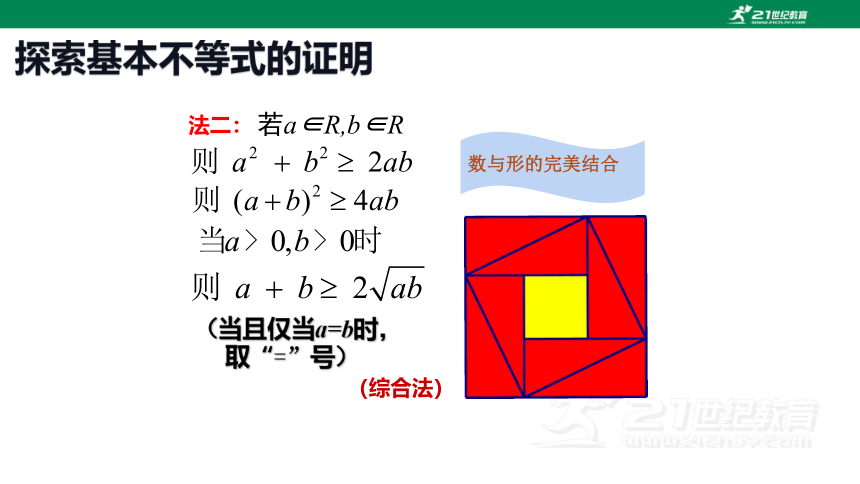
探索基本不等式的证明
数与形的完美结合
法二：
（综合法）
法三：证明：要证
只要证
①
要证①，只要证
②
要证②，只要证
③
显然, ③是成立的.当且仅当a=b时, ③中的等号成立.
分析法
证明不等式：
探索基本不等式的证明
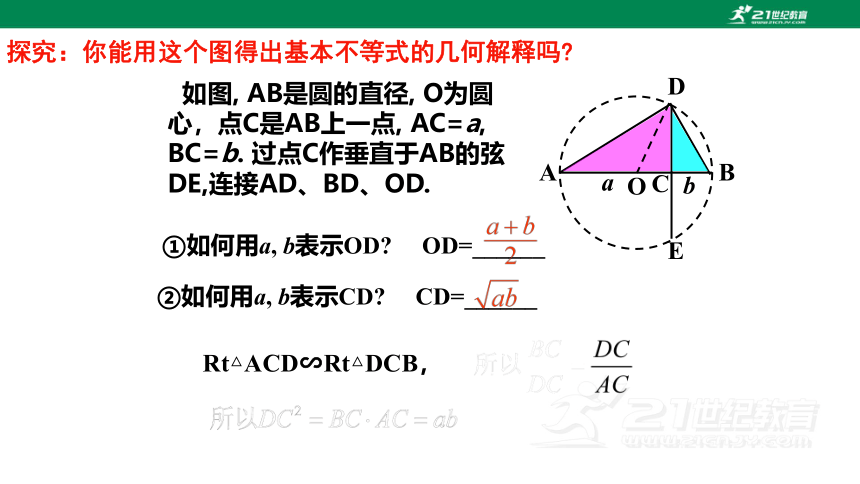
探究：你能用这个图得出基本不等式的几何解释吗
Rt△ACD∽Rt△DCB，
A
B
C
D
E
a
b
O
如图, AB是圆的直径, O为圆 心，点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
②如何用a, b表示CD CD=______
①如何用a, b表示OD OD=______
②如何用a, b表示CD CD=______
①如何用a, b表示OD OD=______
③OD与CD的大小关系怎样 OD_____CD
≥
如图, AB是圆的直径, O为圆心，点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
几何意义：半径不小于半弦长
A
D
B
E
O
C
a
b
探究：你能用这个图得出基本不等式的几何解释吗
1.积为定值求和的最值
例1. 已知x>0，求x+ 的最小值.
探究：不等式x+ ≥1成立吗？能说1是x+ 的最小值吗？
说明：最值必须是存在变量能取到！
变式：
1.判断命题“ 的最小值为2”的真假.
2.已知x>1，求x+ 的最小值.
典例探究：利用基本不等式求最值
例2：(1)如图,用篱笆围成一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时，所用篱笆最短，最短的篱笆是多少？
解：如图设BC=x ，CD=y ，
则xy=100，篱笆的长为2(x+y)m.
当且仅当 时，等号成立
因此，这个矩形的长、宽都为10m时，所用的篱笆最短，最短的篱笆是40m.
此时x=y=10.
x=y
A
B
D
C
若x、y皆为正数，
则当xy为定值P时，当且仅当x=y时，
x+y有最小值_______.
例2：(2)如图，用一段长为36m的篱笆围成一个矩形菜园，问这个矩形菜园的长和宽各为多少时，菜园的面积最大，最大面积是多少？
解：如图，设BC=x ，CD=y ，
则 2(x + y)= 36 , x + y =18
矩形菜园的面积为xy m2
得 xy ≤ 81
当且仅当x=y时，等号成立
因此，这个矩形的长、宽都为9m时，
菜园面积最大，最大面积是81m2
即x=y=9
A
B
D
C
若x、y皆为正数，
则当x+y为定值S时，
当且仅当x=y时，
xy有最大值_______；
C
1.两个 正 数的和为 定 值时，它们的积有最大值，即若x，y∈R＋，且x＋y＝M，M为定值，则
xy ≤
2.两个 正 数的积为 定 值时，它们的和有最小值，即若x， y∈R＋，且xy＝P，P为定值，则
x＋y≥ ，
当且仅当x＝y 时等号成立.
以上是应用基本不等式的原理
触类旁通：从能解一道题到会做一类题
当且仅当x＝y时等号成立.
3、应用基本不等式求最值的条件：
x与y为正实数
若等号成立，x与y必须能够相等
一正
二定
三相等
积定和最小
和定积最大
归纳总结
课堂练习
√
×
×
C
√
1.判断下列结论是否正确.（正确的打“√”，错误的打“×”）
（1） 对于任意 ， ， .( )
（2） 当 时， .( )
（3） 当 时， .( )
（4） 若 ，则 的最小值为 .( )
2.已知 ，则下列不等式正确的是( @7@ ).
A. B.
C. D.
课堂练习
x>2y
[解析] ， ， 都是正数，
， ， ，
，
，
即 ，当且仅当 时，等号成立．
3.不等式 成立的前提条件为_________.
4.已知 ， ， 都是正数，求证： .
课堂练习
5. 某工厂要建造一个长方体形无盖贮水池，其容积 为4 800 m',深为3 m.如果池底每平方米的造价为150元，池壁每平方米的造价为120元，那么怎样设计水池能使总造价最低 最低总造价是多少
答案：
水池底面为边长为20m的正方形能使总造价最低，最低造价是297600元.
课堂总结
2、牢记“一定”、“二正”、“三相等”
1、
作业布置
基础练习
课本第46页练习1-4题
综合运用
课本第48页习题2.2（1，3，4，5题）
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin