【中学教材全解】2013-2014学年高中数学(苏教版必修4)章末练测:第一章 三角函数(含参考答案)
文档属性
| 名称 | 【中学教材全解】2013-2014学年高中数学(苏教版必修4)章末练测:第一章 三角函数(含参考答案) | 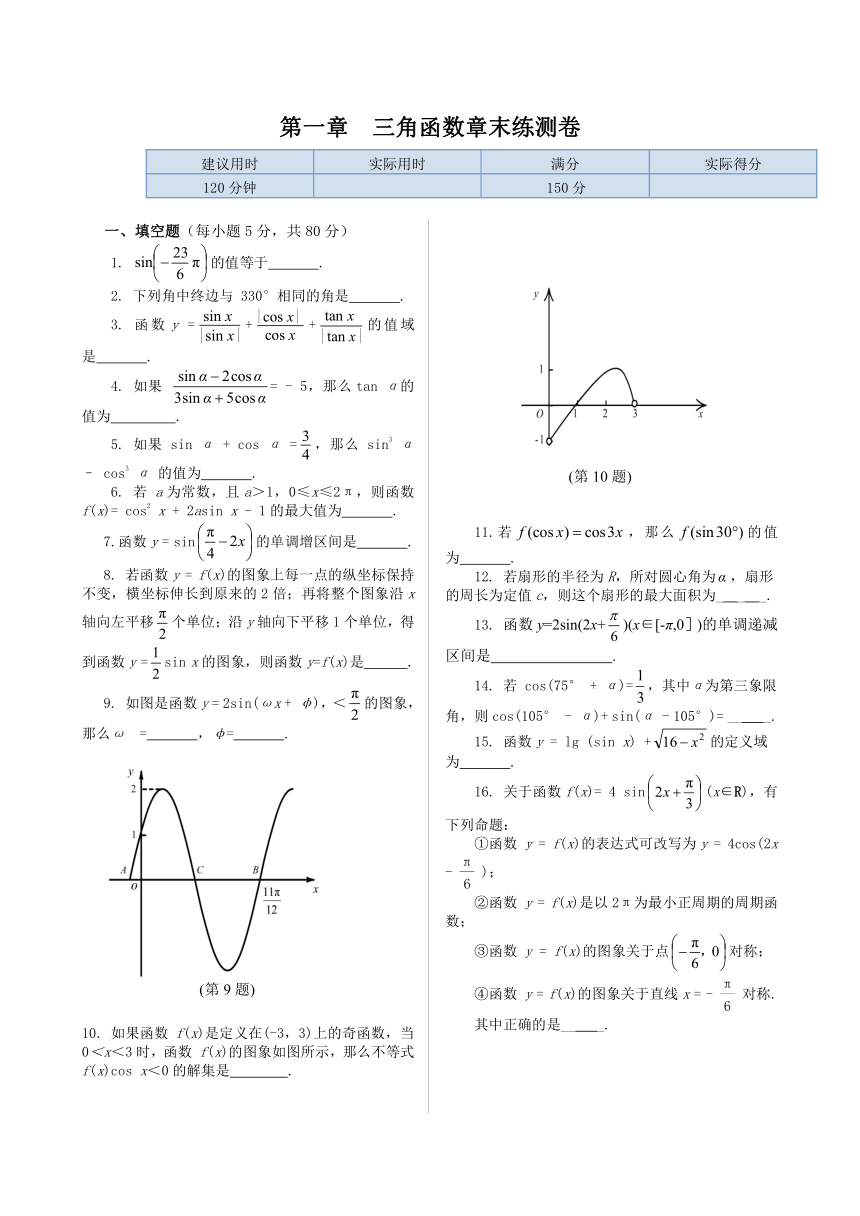 | |
| 格式 | zip | ||
| 文件大小 | 92.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-04 10:00:48 | ||
图片预览



文档简介
第一章 三角函数章末练测卷
建议用时
实际用时
满分
实际得分
120分钟
150分
一、填空题(每小题5分,共80分)
1. 的值等于 .
2. 下列角中终边与 330°相同的角是 .
3. 函数y =++的值域是 .
4. 如果 = - 5,那么tan α的值为 .
5. 如果 sin α + cos α =,那么 sin3 α – cos3 α 的值为 .
6. 若 a为常数,且a>1,0≤x≤2π,则函数f(x)= cos2 x + 2asin x - 1的最大值为 .
7.函数y = sin的单调增区间是 .
8. 若函数y = f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍;再将整个图象沿x轴向左平移个单位;沿y轴向下平移1个单位,得到函数y =sin x的图象,则函数y=f(x)是 .
9. 如图是函数y = 2sin(ωx + φ),<的图象,那么ω?= ,φ= .
10. 如果函数 f(x)是定义在(-3,3)上的奇函数,当0<x<3时,函数 f(x)的图象如图所示,那么不等式f(x)cos x<0的解集是 .
11.若,那么的值为 .
12. 若扇形的半径为R,所对圆心角为,扇形的周长为定值c,则这个扇形的最大面积为_ _ _.
13. 函数y=2sin(2x+)(x∈[-π,0])的单调递减区间是 .
14. 若 cos(75° + α)=,其中α为第三象限角,则cos(105° - α)+ sin(α - 105°)= __ _.
15. 函数y = lg (sin x) +的定义域为 .
16. 关于函数f(x)= 4 sin(x∈R),有下列命题:
①函数 y = f(x)的表达式可改写为y = 4cos(2x - );
②函数 y = f(x)是以2π为最小正周期的周期函数;
③函数 y = f(x)的图象关于点对称;
④函数 y = f(x)的图象关于直线x = - 对称.
其中正确的是__ _.
二、解答题(共70分)
17. (12分)已知角α是第三象限角,
求:(1)角是第几象限的角;(2)角2α终边的位置.
18.(16分)(1)已知角α的终边经过点P(4,- 3),求2sin α + cos α的值;
(2)已知角α的终边经过点P(4a,- 3a)(a≠0),求 2sin α + cos α的值;
(3)已知角α终边上一点P到x轴的距离与到y轴的距离之比为3 : 4,求2sin α + cos α的值.
19.(12分)已知tan α,是关于x的方程x2-kx +k2-3=0的两实根,且3π<α<π,求cos(3π + α)- sin(π + α)的值.
20.(14分)已知0≤x≤,求函数y = cos2 x –
2a cos x的最大值M(a)与最小值m(a).
21. (16分)已知N(2,)是函数y=Asin(ωx+φ)(A>0,ω>0)的图象的最高点,N到相邻最低点的图象曲线与x轴交于A、B,其中B点的坐标(6,0),求此函数的解析表达式.
第一章 三角函数章末练测卷
答题纸
得分:
一、填空题
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11. 12. 13. 14. 15. 16.
三、解答题
17.
18.
19.
20.
21.
第一章 三角函数章末练测卷答案
一、选择题
1. 解析:=.
2. -30° 解析:与 330° 终边相同的角为{α|α = 330° + k ? 360°,k∈Z}.
当 k = - 1时,α = - 30°.
3. {- 1,3} 解析:将x分为第Ⅰ、Ⅱ、Ⅲ、Ⅳ象限四种情况分别讨论,可知值域为{- 1,3}.
4.- 解析:∵ sinα - 2cos α = - 5(3sin α + 5cos α),
∴ 16sin α = - 23cos α,∴ tan α = -.
5. 或- 解析:由已知易得 sin α cos α = -.
∴ |sin3 α - cos3 α| = |(sin α- cos α)(sin2 α + cos2 α sin α cos α)|
= ? |1 + sin α cos α| = .
∴ sin3 α - cos3 α = ±.
6. 解析:f(x)= 1 - sin2 x + 2asin x - 1= - sin2 x + 2asin x.
令sin x = t,∴ t∈[-1,1].
∴ f(t)= - t2 + 2at = -(t - a)2 + a2,t∈[-1,1].
∵a>1,∴ 当t = 1时,函数 f(t)取最大值为2a - 1.
7. ,k∈Z 解析:∵ y = sin(- 2x)= - sin(2x -),∴ + 2kπ ≤ 2x -≤+ 2kπ,∴ + kπ ≤ x ≤+ kπ.
8. y =
9. 2, 解析:因为函数图象过(0,1),所以1=2sinφ,所以sinφ=.
因为|φ|<,所以φ=.故函数y=2sin(ωx+).
又函数图象过点(,0),所以0=2sin(ω?+).
由五点法作图的过程知,ω?+=2π,所以ω=2.综上,φ=,ω=2.
10. ∪(0,1)∪ 解析:由图象可知:0<x<1时,f(x)<0;当1<x<3时,f(x)>0.
再由f(x)是奇函数,知:当﹣1<x<0时,f(x)>0;当﹣3<x<﹣1时,f(x)<0.
又∵当﹣3<x<,或<x<3时,cosx<0;当<x<时,cos x>0.
∴ 当x∈(,1)∪(0,1)∪(,3)时,f(x)?cos x<0.
11. -1
12. 解析:设扇形面积为S,弧长为 .
∴ S = R = (c-2R)· R = -R2 +cR.
∴ 0<R<.当 R = 时,Smax =.
13. [,]
14. 解析:cos(105°-α)+ sin(α -105°) = - cos(75°+α)- sin(α+75°).
∵180°<α<270°,∴ 255°<α+75°<345°.
又cos(α75°) =,∴ sin(α75°)= -.
∴ 原式 =.
15.[-4,-π)∪(0,π)
解析:由已知得
∴ x∈[- 4,- π)∪(0,π).
16. ①③
解析:① f(x)=4sin= 4cos = 4cos = 4cos.
② T == π,最小正周期为π.
③ 令2x += kπ,当 k = 0时,x =,
∴ 函数 f(x)关于点对称.
④ 令2x += kπ+,当 x = -时,k =,与 k∈Z 矛盾.
∴ ①③正确.
二、解答题
17.解:(1)由2kπ + π<α<2kπ +π,k∈Z,
得kπ +<<kπ +π,k∈Z.
将整数 k 分奇数和偶数进行讨论,易得角为第二象限或第四象限的角.
(2)由2kπ + π<α<2kπ +π,k∈Z,
得4kπ + 2π<2α<4kπ + 3π, k∈Z.
∴ 2α终边位置可能在第一象限、第二象限或y轴的非负半轴.
18.解:(1)∵ = 5,
∴ sin α =,cos α =,
∴ 2sin α + cos α =.
(2)∵ ,
∴ 当>0时,∴ r = 5a,sin α =,cos α =.
∴ 2sin α + cos α =;
当 a<0时,∴ r = -5a,sin α =,cos α = -,
∴ 2sin α + cos α =.
(3)当点P在第一象限时, sin α =,cos α =,2sin α + cos α = 2;
当点P在第二象限时, sin α =,cos α =,2sin α + cos α =;
当点P在第三象限时,sin α =,cos α =,2sin α + cos α = - 2;
当点P在第四象限时,sin α =,cos α =,2sin α + cos α =.
19.解:由已知得 tan α· = k2 - 3=1,∴ k =±2.
又 ∵ 3π<α<π,∴ tan α>0,>0.
∴ tan α += k = 2>0 (k = -2舍去),∴tan α= 1,
∴ sin α = cos α = -,
∴ cos(3π +α) - sin(π +α) = sin α - cos α = 0.
20.解:y = cos2 x - 2a cos x = (cos x -a)2 - a2,
令 cosx = t,
∵ 0≤x≤,∴ t∈[0,1].
∴ 原函数可化为f(t) = (t - a)2 - a2,t∈[0,1].
①当 a<0 时,M(a) = f(1) = 1 – 2a,m(a) = f(0) = 0.
②当 0≤a< 时,M(a) = f(1) = 1 – 2a,m(a) = f(a) = –a2.
③当 ≤a≤1 时,M(a) = f(0) = 0,m(a) = f(a) = –a2.
④当 a>1 时,M(a) = f(0) = 0,m(a) = f(1) = 1–2a.
21. 解:∵N(2,)是函数y=Asin(ωx+φ)的图象的一个最高点 , ∴A=.
∵N到相邻最低点的图象曲线与x轴相交于A、B,B点坐标为(6,0),
∴=|xB-xN|=4,∴T=16.又∵T=,∴ω==.∵xN=,
∴xA=2xN-xB=-2,∴A(-2,0),∴y=sin
又∵ 图象过点N(2,∴ ∴ ∴
建议用时
实际用时
满分
实际得分
120分钟
150分
一、填空题(每小题5分,共80分)
1. 的值等于 .
2. 下列角中终边与 330°相同的角是 .
3. 函数y =++的值域是 .
4. 如果 = - 5,那么tan α的值为 .
5. 如果 sin α + cos α =,那么 sin3 α – cos3 α 的值为 .
6. 若 a为常数,且a>1,0≤x≤2π,则函数f(x)= cos2 x + 2asin x - 1的最大值为 .
7.函数y = sin的单调增区间是 .
8. 若函数y = f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍;再将整个图象沿x轴向左平移个单位;沿y轴向下平移1个单位,得到函数y =sin x的图象,则函数y=f(x)是 .
9. 如图是函数y = 2sin(ωx + φ),<的图象,那么ω?= ,φ= .
10. 如果函数 f(x)是定义在(-3,3)上的奇函数,当0<x<3时,函数 f(x)的图象如图所示,那么不等式f(x)cos x<0的解集是 .
11.若,那么的值为 .
12. 若扇形的半径为R,所对圆心角为,扇形的周长为定值c,则这个扇形的最大面积为_ _ _.
13. 函数y=2sin(2x+)(x∈[-π,0])的单调递减区间是 .
14. 若 cos(75° + α)=,其中α为第三象限角,则cos(105° - α)+ sin(α - 105°)= __ _.
15. 函数y = lg (sin x) +的定义域为 .
16. 关于函数f(x)= 4 sin(x∈R),有下列命题:
①函数 y = f(x)的表达式可改写为y = 4cos(2x - );
②函数 y = f(x)是以2π为最小正周期的周期函数;
③函数 y = f(x)的图象关于点对称;
④函数 y = f(x)的图象关于直线x = - 对称.
其中正确的是__ _.
二、解答题(共70分)
17. (12分)已知角α是第三象限角,
求:(1)角是第几象限的角;(2)角2α终边的位置.
18.(16分)(1)已知角α的终边经过点P(4,- 3),求2sin α + cos α的值;
(2)已知角α的终边经过点P(4a,- 3a)(a≠0),求 2sin α + cos α的值;
(3)已知角α终边上一点P到x轴的距离与到y轴的距离之比为3 : 4,求2sin α + cos α的值.
19.(12分)已知tan α,是关于x的方程x2-kx +k2-3=0的两实根,且3π<α<π,求cos(3π + α)- sin(π + α)的值.
20.(14分)已知0≤x≤,求函数y = cos2 x –
2a cos x的最大值M(a)与最小值m(a).
21. (16分)已知N(2,)是函数y=Asin(ωx+φ)(A>0,ω>0)的图象的最高点,N到相邻最低点的图象曲线与x轴交于A、B,其中B点的坐标(6,0),求此函数的解析表达式.
第一章 三角函数章末练测卷
答题纸
得分:
一、填空题
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11. 12. 13. 14. 15. 16.
三、解答题
17.
18.
19.
20.
21.
第一章 三角函数章末练测卷答案
一、选择题
1. 解析:=.
2. -30° 解析:与 330° 终边相同的角为{α|α = 330° + k ? 360°,k∈Z}.
当 k = - 1时,α = - 30°.
3. {- 1,3} 解析:将x分为第Ⅰ、Ⅱ、Ⅲ、Ⅳ象限四种情况分别讨论,可知值域为{- 1,3}.
4.- 解析:∵ sinα - 2cos α = - 5(3sin α + 5cos α),
∴ 16sin α = - 23cos α,∴ tan α = -.
5. 或- 解析:由已知易得 sin α cos α = -.
∴ |sin3 α - cos3 α| = |(sin α- cos α)(sin2 α + cos2 α sin α cos α)|
= ? |1 + sin α cos α| = .
∴ sin3 α - cos3 α = ±.
6. 解析:f(x)= 1 - sin2 x + 2asin x - 1= - sin2 x + 2asin x.
令sin x = t,∴ t∈[-1,1].
∴ f(t)= - t2 + 2at = -(t - a)2 + a2,t∈[-1,1].
∵a>1,∴ 当t = 1时,函数 f(t)取最大值为2a - 1.
7. ,k∈Z 解析:∵ y = sin(- 2x)= - sin(2x -),∴ + 2kπ ≤ 2x -≤+ 2kπ,∴ + kπ ≤ x ≤+ kπ.
8. y =
9. 2, 解析:因为函数图象过(0,1),所以1=2sinφ,所以sinφ=.
因为|φ|<,所以φ=.故函数y=2sin(ωx+).
又函数图象过点(,0),所以0=2sin(ω?+).
由五点法作图的过程知,ω?+=2π,所以ω=2.综上,φ=,ω=2.
10. ∪(0,1)∪ 解析:由图象可知:0<x<1时,f(x)<0;当1<x<3时,f(x)>0.
再由f(x)是奇函数,知:当﹣1<x<0时,f(x)>0;当﹣3<x<﹣1时,f(x)<0.
又∵当﹣3<x<,或<x<3时,cosx<0;当<x<时,cos x>0.
∴ 当x∈(,1)∪(0,1)∪(,3)时,f(x)?cos x<0.
11. -1
12. 解析:设扇形面积为S,弧长为 .
∴ S = R = (c-2R)· R = -R2 +cR.
∴ 0<R<.当 R = 时,Smax =.
13. [,]
14. 解析:cos(105°-α)+ sin(α -105°) = - cos(75°+α)- sin(α+75°).
∵180°<α<270°,∴ 255°<α+75°<345°.
又cos(α75°) =,∴ sin(α75°)= -.
∴ 原式 =.
15.[-4,-π)∪(0,π)
解析:由已知得
∴ x∈[- 4,- π)∪(0,π).
16. ①③
解析:① f(x)=4sin= 4cos = 4cos = 4cos.
② T == π,最小正周期为π.
③ 令2x += kπ,当 k = 0时,x =,
∴ 函数 f(x)关于点对称.
④ 令2x += kπ+,当 x = -时,k =,与 k∈Z 矛盾.
∴ ①③正确.
二、解答题
17.解:(1)由2kπ + π<α<2kπ +π,k∈Z,
得kπ +<<kπ +π,k∈Z.
将整数 k 分奇数和偶数进行讨论,易得角为第二象限或第四象限的角.
(2)由2kπ + π<α<2kπ +π,k∈Z,
得4kπ + 2π<2α<4kπ + 3π, k∈Z.
∴ 2α终边位置可能在第一象限、第二象限或y轴的非负半轴.
18.解:(1)∵ = 5,
∴ sin α =,cos α =,
∴ 2sin α + cos α =.
(2)∵ ,
∴ 当>0时,∴ r = 5a,sin α =,cos α =.
∴ 2sin α + cos α =;
当 a<0时,∴ r = -5a,sin α =,cos α = -,
∴ 2sin α + cos α =.
(3)当点P在第一象限时, sin α =,cos α =,2sin α + cos α = 2;
当点P在第二象限时, sin α =,cos α =,2sin α + cos α =;
当点P在第三象限时,sin α =,cos α =,2sin α + cos α = - 2;
当点P在第四象限时,sin α =,cos α =,2sin α + cos α =.
19.解:由已知得 tan α· = k2 - 3=1,∴ k =±2.
又 ∵ 3π<α<π,∴ tan α>0,>0.
∴ tan α += k = 2>0 (k = -2舍去),∴tan α= 1,
∴ sin α = cos α = -,
∴ cos(3π +α) - sin(π +α) = sin α - cos α = 0.
20.解:y = cos2 x - 2a cos x = (cos x -a)2 - a2,
令 cosx = t,
∵ 0≤x≤,∴ t∈[0,1].
∴ 原函数可化为f(t) = (t - a)2 - a2,t∈[0,1].
①当 a<0 时,M(a) = f(1) = 1 – 2a,m(a) = f(0) = 0.
②当 0≤a< 时,M(a) = f(1) = 1 – 2a,m(a) = f(a) = –a2.
③当 ≤a≤1 时,M(a) = f(0) = 0,m(a) = f(a) = –a2.
④当 a>1 时,M(a) = f(0) = 0,m(a) = f(1) = 1–2a.
21. 解:∵N(2,)是函数y=Asin(ωx+φ)的图象的一个最高点 , ∴A=.
∵N到相邻最低点的图象曲线与x轴相交于A、B,B点坐标为(6,0),
∴=|xB-xN|=4,∴T=16.又∵T=,∴ω==.∵xN=,
∴xA=2xN-xB=-2,∴A(-2,0),∴y=sin
又∵ 图象过点N(2,∴ ∴ ∴
