人教版(2019)数学必修第一册 3.1.2函数的表示法(2) 课件(共34张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第一册 3.1.2函数的表示法(2) 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 890.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
函数的表示法(2)
1.了解分段函数的概念,会求分段函数的函数值,能画出分段函数的图象.
2.能在实际问题中列出分段函数,并能解决有关问题.
本节目标
课前预习
(1)什么是分段函数?分段函数是一个还是几个函数?
(2)怎样求分段函数的值?如何画分段函数的图象?
预习课本P68~71,思考并完成以下问题
课前小测
1.已知函数f(x)= 则f(1)等于( )
A.0 B.1 C. D.2
B
f(1)= =1
2.函数f(x)= 的定义域为________.
[1,+∞)
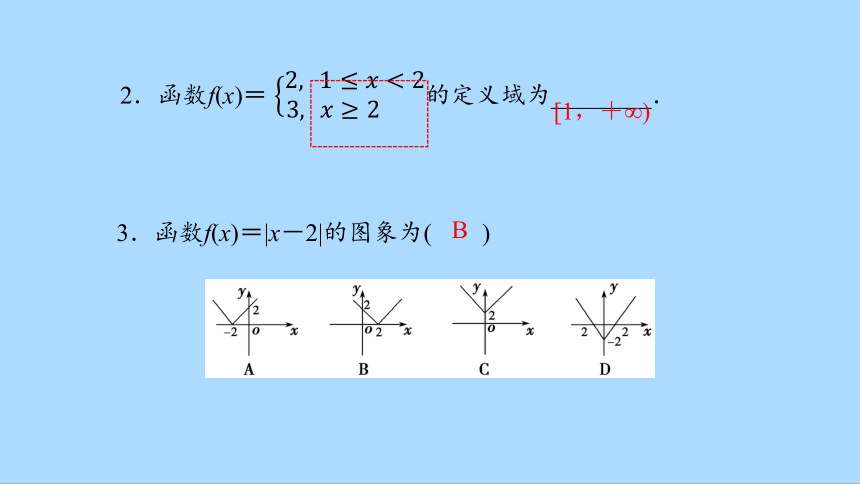
3.函数f(x)=|x-2|的图象为( )
B
4.设函数f(x)= ,则f(f(3))=( )
A. B.3 C. D.
D
f(3)=
f(f(3))= f() = =
新知探究
(1)分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的__________的函数.
(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的________;各段函数的定义域的交集是_______.
分段函数
对应关系
并集
空集
(1)分段函数虽然由几部分构成,但它仍是一个函数而不是几个函数.
(2)分段函数的“段”可以是等长的,也可以是不等长的.
知识点睛
如y= 其“段”是不等长的.
题型突破
典例深度剖析 重点多维探究
题型一 分段函数的求值问题
[例1] 已知函数f(x)= .
(1)求f(-5),f(-),的值;
(2)若f(a)=3,求实数a的值.
[例1] 已知函数f(x)= .
(1)求f(-5),f(-),的值;
由-5∈(-∞,-2],- ∈(-2,2),- ∈(-∞,-2],
知f(-5)=-5+1=-4,f(- )=(- )2+2×(- )=3-2.
∵f =- +1=- ,而-2<-<2,
∴f =f = 2+2×= -3=-.
[例1] 已知函数f(x)= .
(2)若f(a)=3,求实数a的值.
当a≤-2时,a+1=3,即a=2>-2,不合题意,舍去.
当-2∴(a-1)(a+3)=0,解得a=1或a=-3.
∵1∈(-2,2),-3 (-2,2),∴a=1符合题意.
当a≥2时,2a-1=3,即a=2符合题意.
综上可得,当f(a)=3时,a=1或a=2.
(1)确定要求值的自变量属于哪一段区间.
(2)代入该段的解析式求值,直到求出值为止.
当出现f(f(x0))的形式时,应从内到外依次求值.
方法总结
分段函数求函数值的方法
已知分段函数的函数值求自变量取值的步骤
(1)先对字母的取值范围分类讨论.
(2)然后代入不同的解析式中.
(3)通过解方程求出字母的值.
(4)检验所求的值是否在所讨论的区间内.
解题策略
技巧点拨
求某条件下自变量的值时,先假设所求的值在分段函数定义区间的各段上,然后相应求出自变量的值,切记代入检验.
跟踪训练
1.函数f(x)= ,则f(7)=________.
f(7)=f(f(12))=f(9)=f(f(14))=f(11)=8
8
题型二 分段函数的解析式
[例2] 如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2 cm,当垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y关于x的函数解析式,并画出大致图象.
按点E所在的位置分E在线段AB,E在线段AD及E在线段CD三类分别求解.
思路点拨
过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.
因为四边形ABCD是等腰梯形,底角为45°,AB=2 cm,
所以BG=AG=DH=HC=2 cm,
又BC=7 cm,所以AD=GH=3 cm.
(1)当点F在BG上,即x∈[0,2]时,y=x2;
(2)当点F在GH上,即x∈(2,5]时,y= ×2=2x-2;
(3)当点F在HC上,即x∈(5,7]时,y=S五边形ABFED=S梯形ABCD-SRt△CEF= (7+3)×2- (7-x)2=- (x-7)2+10.
综合函数的解析式为y=
[例2] 如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2 cm,当垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y关于x的函数解析式,并画出大致图象.
1.当目标在不同区间有不同的计算表达方式时,往往需要用分段函数模型来表示两变量间的对应关系,而分段函数图象也需要分段画.
2.通过本例让学生初步尝试用分段函数解决实际问题的意识,培养学生的建模素养.
反思感悟
跟踪训练
2.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按照5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
设票价为y元,里程为x公里,定义域为(0,20].
由题意得函数的解析式如下:
y=
函数图象如图所示:
2.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按照5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
题型三 分段函数的图象及应用
[探究问题]
1.函数f(x)=|x-2|能用分段函数的形式表示吗?能否作出其图象?
提示:能.f(x)=
函数f(x)的图象如图所示.
2.结合探究点1,你能说一下画含有绝对值的函数图象的方法吗?
[探究问题]
提示:含有绝对值的函数,要作出其图象,首先应根据绝对值的意义去掉绝对值符号,将函数转化为分段函数,然后分段作出函数图象.
[例3] 已知函数f(x)=1+ (-2(1)用分段函数的形式表示f(x);
(2)画出f(x)的图象;
(3)写出函数f(x)的值域.
(1)分-2(2)利用(1)的结论可画图象;
(3) 找到图象最高点和最低点的纵坐标,可得值域.
思路点拨
[例3] 已知函数f(x)=1+ (-2(1)用分段函数的形式表示f(x);
(1)当0≤x≤2时,f(x)=1+ =1,
当-2∴f(x)=
(2)函数f(x)的图象如图所示.
(3)由(2)知,f(x)在(-2,2]上的值域为[1,3).
(2)画出f(x)的图象;
(3)写出函数f(x)的值域.
多维训练
变式 已知函数f(x)=|x|-2.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)写出函数f(x)的值域.
f(x)=|x|-2=
由图可知,f(x)的值域为[-2,+∞).
作分段函数的图象时,分别作出各段的图象,在作每一段图象时,先不管定义域的限制,作出其图象,再保留定义域内的一段图象即可,作图时要特别注意接点处点的虚实,保证不重不漏.
分段函数图象的画法
方法总结
随堂检测
1.思考辨析
(1)分段函数由几个函数构成.( )
(2)函数f(x)= 是分段函数.( )
×
√
2.设函数f(x)= ,则f(f(6))=( )
A. B.1 C. D.
∵f(6)= = ≤1,
∴f(f(6))=()2 1=
C
3.函数y=f(x)的图象如图所示,则其解析式为________________.
当0≤x≤1时,设f(x)=kx,又过点(1,2),故k=2,
∴f(x)=2x;
当1当x≥2时,f(x)=3.
综上f(x)=
f(x)=
4.已知f(x)=
(1)画出f(x)的图象; (2)求f(x)的定义域和值域.
由条件知,函数f(x)的定义域为R.
由图象知,
当-1≤x≤1时,f(x)=x2的值域为[0,1],
当x>1或x<-1时,f(x)=1,
所以f(x)的值域为[0,1].
1.分段函数是一个函数,而不是几个函数.
2.分段函数求值要先找准自变量所在的区间;分段函数的定义域、值域分别是各段函数的定义域、值域的并集.
3.分段函数的图象
分段函数有几段,它的图象就由几条曲线组成.在同一直角坐标系中,根据每段的定义区间和表达式依次画出图象,要注意确定每段图象的端点是空心点还是实心点,各段函数图象组合到一起就可得到整个分段函数的图象.
本课小结
函数的表示法(2)
1.了解分段函数的概念,会求分段函数的函数值,能画出分段函数的图象.
2.能在实际问题中列出分段函数,并能解决有关问题.
本节目标
课前预习
(1)什么是分段函数?分段函数是一个还是几个函数?
(2)怎样求分段函数的值?如何画分段函数的图象?
预习课本P68~71,思考并完成以下问题
课前小测
1.已知函数f(x)= 则f(1)等于( )
A.0 B.1 C. D.2
B
f(1)= =1
2.函数f(x)= 的定义域为________.
[1,+∞)
3.函数f(x)=|x-2|的图象为( )
B
4.设函数f(x)= ,则f(f(3))=( )
A. B.3 C. D.
D
f(3)=
f(f(3))= f() = =
新知探究
(1)分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的__________的函数.
(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的________;各段函数的定义域的交集是_______.
分段函数
对应关系
并集
空集
(1)分段函数虽然由几部分构成,但它仍是一个函数而不是几个函数.
(2)分段函数的“段”可以是等长的,也可以是不等长的.
知识点睛
如y= 其“段”是不等长的.
题型突破
典例深度剖析 重点多维探究
题型一 分段函数的求值问题
[例1] 已知函数f(x)= .
(1)求f(-5),f(-),的值;
(2)若f(a)=3,求实数a的值.
[例1] 已知函数f(x)= .
(1)求f(-5),f(-),的值;
由-5∈(-∞,-2],- ∈(-2,2),- ∈(-∞,-2],
知f(-5)=-5+1=-4,f(- )=(- )2+2×(- )=3-2.
∵f =- +1=- ,而-2<-<2,
∴f =f = 2+2×= -3=-.
[例1] 已知函数f(x)= .
(2)若f(a)=3,求实数a的值.
当a≤-2时,a+1=3,即a=2>-2,不合题意,舍去.
当-2
∵1∈(-2,2),-3 (-2,2),∴a=1符合题意.
当a≥2时,2a-1=3,即a=2符合题意.
综上可得,当f(a)=3时,a=1或a=2.
(1)确定要求值的自变量属于哪一段区间.
(2)代入该段的解析式求值,直到求出值为止.
当出现f(f(x0))的形式时,应从内到外依次求值.
方法总结
分段函数求函数值的方法
已知分段函数的函数值求自变量取值的步骤
(1)先对字母的取值范围分类讨论.
(2)然后代入不同的解析式中.
(3)通过解方程求出字母的值.
(4)检验所求的值是否在所讨论的区间内.
解题策略
技巧点拨
求某条件下自变量的值时,先假设所求的值在分段函数定义区间的各段上,然后相应求出自变量的值,切记代入检验.
跟踪训练
1.函数f(x)= ,则f(7)=________.
f(7)=f(f(12))=f(9)=f(f(14))=f(11)=8
8
题型二 分段函数的解析式
[例2] 如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2 cm,当垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y关于x的函数解析式,并画出大致图象.
按点E所在的位置分E在线段AB,E在线段AD及E在线段CD三类分别求解.
思路点拨
过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.
因为四边形ABCD是等腰梯形,底角为45°,AB=2 cm,
所以BG=AG=DH=HC=2 cm,
又BC=7 cm,所以AD=GH=3 cm.
(1)当点F在BG上,即x∈[0,2]时,y=x2;
(2)当点F在GH上,即x∈(2,5]时,y= ×2=2x-2;
(3)当点F在HC上,即x∈(5,7]时,y=S五边形ABFED=S梯形ABCD-SRt△CEF= (7+3)×2- (7-x)2=- (x-7)2+10.
综合函数的解析式为y=
[例2] 如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2 cm,当垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y关于x的函数解析式,并画出大致图象.
1.当目标在不同区间有不同的计算表达方式时,往往需要用分段函数模型来表示两变量间的对应关系,而分段函数图象也需要分段画.
2.通过本例让学生初步尝试用分段函数解决实际问题的意识,培养学生的建模素养.
反思感悟
跟踪训练
2.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按照5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
设票价为y元,里程为x公里,定义域为(0,20].
由题意得函数的解析式如下:
y=
函数图象如图所示:
2.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按照5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
题型三 分段函数的图象及应用
[探究问题]
1.函数f(x)=|x-2|能用分段函数的形式表示吗?能否作出其图象?
提示:能.f(x)=
函数f(x)的图象如图所示.
2.结合探究点1,你能说一下画含有绝对值的函数图象的方法吗?
[探究问题]
提示:含有绝对值的函数,要作出其图象,首先应根据绝对值的意义去掉绝对值符号,将函数转化为分段函数,然后分段作出函数图象.
[例3] 已知函数f(x)=1+ (-2
(2)画出f(x)的图象;
(3)写出函数f(x)的值域.
(1)分-2
(3) 找到图象最高点和最低点的纵坐标,可得值域.
思路点拨
[例3] 已知函数f(x)=1+ (-2
(1)当0≤x≤2时,f(x)=1+ =1,
当-2
(2)函数f(x)的图象如图所示.
(3)由(2)知,f(x)在(-2,2]上的值域为[1,3).
(2)画出f(x)的图象;
(3)写出函数f(x)的值域.
多维训练
变式 已知函数f(x)=|x|-2.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)写出函数f(x)的值域.
f(x)=|x|-2=
由图可知,f(x)的值域为[-2,+∞).
作分段函数的图象时,分别作出各段的图象,在作每一段图象时,先不管定义域的限制,作出其图象,再保留定义域内的一段图象即可,作图时要特别注意接点处点的虚实,保证不重不漏.
分段函数图象的画法
方法总结
随堂检测
1.思考辨析
(1)分段函数由几个函数构成.( )
(2)函数f(x)= 是分段函数.( )
×
√
2.设函数f(x)= ,则f(f(6))=( )
A. B.1 C. D.
∵f(6)= = ≤1,
∴f(f(6))=()2 1=
C
3.函数y=f(x)的图象如图所示,则其解析式为________________.
当0≤x≤1时,设f(x)=kx,又过点(1,2),故k=2,
∴f(x)=2x;
当1
综上f(x)=
f(x)=
4.已知f(x)=
(1)画出f(x)的图象; (2)求f(x)的定义域和值域.
由条件知,函数f(x)的定义域为R.
由图象知,
当-1≤x≤1时,f(x)=x2的值域为[0,1],
当x>1或x<-1时,f(x)=1,
所以f(x)的值域为[0,1].
1.分段函数是一个函数,而不是几个函数.
2.分段函数求值要先找准自变量所在的区间;分段函数的定义域、值域分别是各段函数的定义域、值域的并集.
3.分段函数的图象
分段函数有几段,它的图象就由几条曲线组成.在同一直角坐标系中,根据每段的定义区间和表达式依次画出图象,要注意确定每段图象的端点是空心点还是实心点,各段函数图象组合到一起就可得到整个分段函数的图象.
本课小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
