人教版(2019)数学必修第一册期末复习:函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用 课件(共50张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第一册期末复习:函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用 课件(共50张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-11 00:00:00 | ||
图片预览










文档简介
(共50张PPT)
函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
考纲分析
课程标准解读 关联考点 核心素养
1.了解函数y=Asin(ωx+φ)的物理意义;能画出y=Asin(ωx+φ)的图象,了解参数A,ω,φ对函数图象变化的影响. 2.了解三角函数是描述周期变化现象的重要函数模型,会利用三角函数模型解决一些简单的实际问题. 1.“五点法”作图及图象变换. 2.求函数y=Asin(ωx+φ)的解析式. 3.三角函数图象与性质的综合问题. 1.直观想象.
2.数学建模.
3.数学运算.
课前自测
(5)若函数y=Asin(ωx+φ)为偶函数,则φ=2kπ+(k∈Z).( )
1.判断正误(正确的打“√”,错误的打“×”)
(1)把y=sin x的图象上各点的横坐标缩短为原来的,纵坐标不变,所得图象对应的函数解析式为y=sin x.( )
×
(2)将y=sin 2x的图象向右平移个单位长度,得到y=sin 的图象.( )
×
(3)函数f(x)=Asin(ωx+φ)(A≠0)的最大值为A,最小值为-A.( )
×
(4)如果y=Acos(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心之间的距离为.( )
√
×
2.为了得到y=3cos 的图象,只需把y=3cos 图象上的所有点的( )
A.纵坐标伸长到原来的3倍,横坐标不变
B.横坐标伸长到原来的3倍,纵坐标不变
C.纵坐标缩短到原来的,横坐标不变
D.横坐标缩短到原来的,纵坐标不变
D
√
3.(易错题)要得到函数y=sin 的图象,只需将函数y=sin 4x的图象( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
y=sin
向左平移个单位长度
y=sin 4x的图象
y=sin 的图象
A
4.若将函数y=2sin 2x的图象向左平移个单位长度,则得到的图象对应的函数表达式为f(x)=_____________.
y=2sin 2x
向左平移个单位长度
f(x)=2sin
=2sin
2sin
5.已知函数f(x)=2sin(ωx+φ) 的部分图象如图所示,则f(x)=_____________.
所以f(x)=2sin (2x-).
设f(x)的最小正周期为T,
根据题图可知, = ,
所以T=π,故ω=2,
根据2sin=0(增区间上的零点)
可知, +φ=2kπ,k∈Z,
即φ=2kπ-,k∈Z,
又|φ|< ,故φ=-.
2sin (2x-)
考点梳理
1.y=Asin(ωx+φ)的有关概念
y=Asin(ωx+φ)(A>0,ω>0),x∈[0,+∞)表示一个振动量时 振幅 周期 频率 相位 初相
A T= f== ωx+φ φ
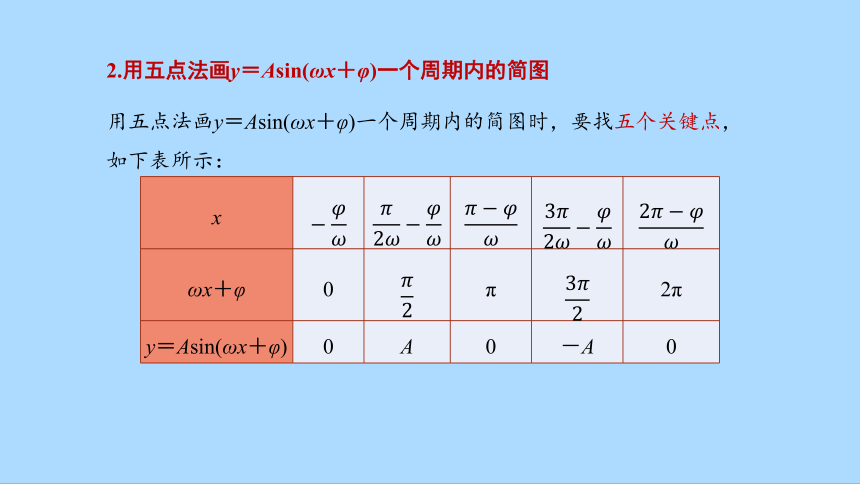
2.用五点法画y=Asin(ωx+φ)一个周期内的简图
用五点法画y=Asin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示:
x
ωx+φ 0 π 2π
y=Asin(ωx+φ) 0 A 0 -A 0
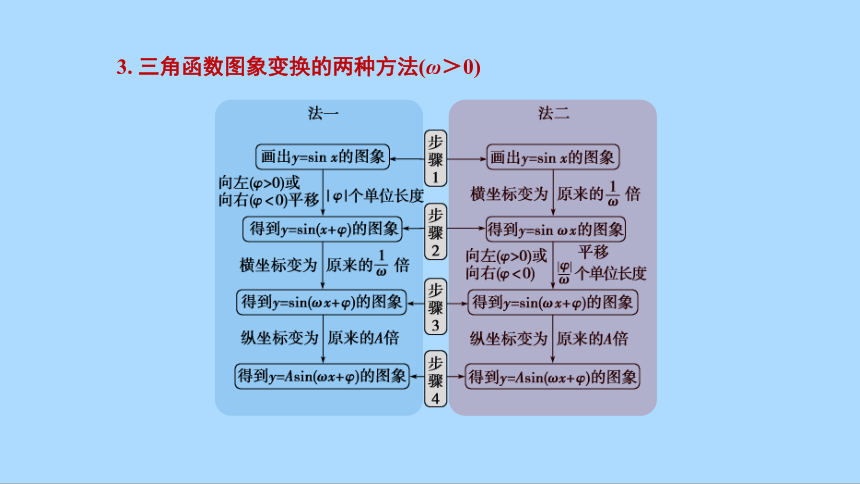
3. 三角函数图象变换的两种方法(ω>0)
常用结论
(1)对称中心与零点相联系,对称轴与最值点相联系.y=Asin(ωx+φ)的图象有无数条对称轴,可由方程ωx+φ=kπ+(k∈Z)解出;它还有无数个对称中心,即图象与x轴的交点,可由ωx+φ=kπ(k∈Z)解出.
(2)相邻两条对称轴间的距离为,相邻两对称中心间的距离也为,函数的对称轴一定经过图象的最高点或最低点.
常用结论
1
对称中心与零点相联系,对称轴与最值点相联系.y=Asin(ωx+φ)的图象有无数条对称轴,可由方程ωx+φ=kπ+(k∈Z)解出;它还有无数个对称中心,即图象与x轴的交点,可由ωx+φ=kπ(k∈Z)解出.
2
相邻两条对称轴间的距离为,相邻两对称中心间的距离也为,函数的对称轴一定经过图象的最高点或最低点.
常见误区
(2)由y=sin ωx到y=sin(ωx+φ)(ω>0,φ>0)的变换:向左平移个单位长度而非φ个单位长度.
!
(1)函数y=Asin(ωx+φ)+k图象平移的规律:“左加右减,上加下减”.
典例剖析
考点
1
五点法作图及图象变换
[例1] 已知函数f(x)= sin 2x+2cos2x+a,其最大值为2.
(1)求a的值及f(x)的最小正周期;
(2)画出f(x)在[0,π]上的图象.
最小正周期T= =π.
[例1] 已知函数f(x)= sin 2x+2cos2x+a,其最大值为2.
(1)求a的值及f(x)的最小正周期;
f(x)= sin 2x+2cos2x+a
= sin 2x+cos 2x+1+a
=2sin (2x)+1+a
f(x)的最大值为2,
所以a=-1,
[例1] 已知函数f(x)= sin 2x+2cos2x+a,其最大值为2.
(2)画出f(x)在[0,π]上的图象.
x 0 π
2x+ π 2π
f(x)=2sin(2x) 1 2 0 -2 0 1
由(1)知f(x)=2sin (2x) ,列表:
[例1] 已知函数f(x)= sin 2x+2cos2x+a,其最大值为2.
(2)画出f(x)在[0,π]上的图象.
画图如下.
变式探究
1.(变问法)若将本例中函数f(x)的图象向左平移个单位长度,把所有点的横坐标伸长到原来的二倍(纵坐标不变),得到函数g(x)的图象,则g(x)=________________.
由[例1]知f(x)=2sin (2x) ,
向左平移个单位长度
f(x)=2sin [2(x) ]
=2sin (2x)
把所有点的横坐标伸长到原来的二倍(纵坐标不变)
g(x) =2sin (x)
f(x)=2sin (2x)
2sin (x)
2.(变问法)在本例条件下,函数y=2cos 2x的图象向右平移________个单位得到y=f(x)的图象.
由[例1]知f(x)=2sin (2x) ,
向右平移个单位长度
向左平移个单位长度
y=2cos 2x
y=2sin(2x+)
y=2sin 2x
方法总结
函数y=Asin(ωx+φ)(A>0,ω>0的图象的两种作法
五点法 设z=ωx+φ,由z取0,,π,π,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象
图象变 换法 由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)的图象,有两种主要途径“先平移后伸缩”与“先伸缩后平移”
平移变换和伸缩变换都是针对x而言,即x本身加减多少值,而不是ωx加减多少值.
注意
跟踪训练
1.函数y= sin 的图象向左平移φ个单位长度,得到的函数是偶函数,则φ的最小正值是( )
A. B. C. D.
由k=0可得φ的最小正值是.
函数y=sin 向左平移φ个单位长度可得y=sin ,
因为y= sin 是偶函数,
所以2φ+ = +kπ,k∈Z,φ= + ,k∈Z,
A
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
A.f(x)与g(x)的图象重合
B. 为f(x)图象的一个对称中心
C.直线x=-为函数g(x)图象的一条对称轴
D.f(x)的图象向左平移个单位长度可得g(x)的图象
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
①
y=sin x
向左平移个单位长度
y=sin
各点的横坐标缩短到原来的倍
f(x)=sin
②
y=sin x
各点的横坐标缩短到原来的倍
y=sin 2x
向左平移个单位长度
g(x)=sin
=sin
A.f(x)与g(x)的图象重合
×
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
A.f(x)与g(x)的图象重合
×
B. 为f(x)图象的一个对称中心
令2x+ =kπ(k∈Z),得
令k=1,则可知选项B正确;
x=π-(k∈Z),
√
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
A.f(x)与g(x)的图象重合
×
B. 为f(x)图象的一个对称中心
√
C.直线x=-为函数g(x)图象的一条对称轴
令k=-1,则可知选项C正确.
令2x+=kπ +(k∈Z),得x= +(k∈Z),
√
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
A.f(x)与g(x)的图象重合
×
B. 为f(x)图象的一个对称中心
√
C.直线x=-为函数g(x)图象的一条对称轴
√
D.f(x)的图象向左平移个单位长度可得g(x)的图象
g(x)=sin=sin[2 ]=f ,
所以f(x)的图象向左平移个单位长度可得g(x)的图象.
√
BCD
考点
2
求y=Asin(ωx+φ)的解析式
[例2] (多选)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)=( )
A.sin B.sin
C.cos D.cos
[例2] (多选)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)=( )
A.sin B.sin
C.cos D.cos
由题图可知,函数的最小正周期T=2=π,
所以=π,ω=±2.
当ω=2时,y=sin(2x+φ),
将点代入得,sin =0,
所以2× +φ=2kπ+π,k∈Z,即φ=2kπ+,k∈Z,
故y=sin.
由于y=sin=sin[π-(2x+)]=sin,故选项B正确;
y=sin(-2x)=cos =cos,选项C正确;
√
√
对于选项A,当x=时, sin=1≠0,错误;
×
[例2] (多选)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)=( )
A.sin B.sin
C.cos D.cos
√
√
×
对于选项D,当x= = 时,cos=1≠-1,错误.
×
当ω=-2时,y=sin(-2x+φ),将代入,得sin(-2×+φ)=0,结合函数图象,知-2×+φ=π+2kπ,k∈Z,得φ=+2kπ,k∈Z,所以y=sin (-2x+) ,但当x=0时,y=sin(-2x+)=-<0,与图象不符合,舍去.
BC
方法总结
②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:
“最大值点”(即图象的“峰点”)时ωx+φ = +2kπ(k∈Z);“最小值点”(即图象的“谷点”)时ωx+φ= +2kπ(k∈Z).
(1)求A,b,确定函数的最大值M和最小值m,
则A= ,b= .
(2)求ω,确定函数的最小正周期T,则可得ω= .
(3)求φ,常用的方法有:
①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上);
确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法
跟踪训练
1.已知函数f(x)=Asin(ωx+φ) 的最小正周期是π,且当x= 时,f(x)取得最大值2,则f(x)=______________.
所以φ= ,所以函数y=f(x)的解析式为f(x)=2sin.
因为函数f(x)的最小正周期是π,所以ω=2.
又因为x=时,f(x)取得最大值2.
所以A=2,
同时2×+φ=2kπ+,k∈Z,
φ=2kπ+,k∈Z,因为-<φ< ,
2sin
2.已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG(点G是图象的最高点)是边长为2的等边三角形,则f(1)=________.
所以f(x)= cos (x+ ),
由题意得,A=,T=4=,ω=.
又因为f(x)=Acos(ωx+φ)为奇函数,
所以φ=+kπ,k∈Z,
由0<φ<π,取k=0,则φ=,
所以f(1)=-.
-
考点
3
函数y=Asin(ωx+φ)图象与性质的综合应用
角度一 三角函数模型的应用
[例3] 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到地面的距离是________米.
当t=40时,f(t)=3-2cos =4(米).
[例3] 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到地面的距离是________米.
以圆心O1为原点,以水平方向为x轴方向,以竖直方向为y轴方向建立平面直角坐标系,
因为大风车的半径为2米,圆上最低点O离地面1米,
12秒旋转一周,
设∠OO1P=θ,运动t秒后与地面的距离为f(t),又周期T=12,
所以θ= ·2π= t,
f(t)=3+2sin =3-2cos t (t≥0),
4
方法总结
需要建立精确的或者数据拟合的模型去解决问题,尤其是利用已知数据建立拟合函数解决实际问题,此类问题体现了数学建模核心素养,考查应用意识.
利用三角函数的有关性质解决问题,其关键是准确理解自变量的意义及自变量与因变量之间的对应法则;
(1)已知函数模型
(2)需要建立函数模型
三角函数模型在实际应用中体现的两个方面
角度二 方程根(函数零点)问题
[例4] 函数y=sin 2x+cos 2x-m在上有两个不同的零点,则m的取值范围是________.
所以y=和y=sin t,t∈的图象有两个不同交点,如图:
函数y=sin 2x+cos 2x-m在上有两个不同的零点,
转化为m=cos 2x+ sin 2x=2sin ,在x∈上有两个不同的实数根.
设2x+=t,则t∈,
所以题目条件可转化为=sin t,在t∈上有两个不同的实数根.
由图象观察知, 的取值范围是,
故m的取值范围是(-2,-1).
角度二 方程根(函数零点)问题
[例4] 函数y=sin 2x+cos 2x-m在上有两个不同的零点,则m的取值范围是_____________.
(-2,-1)
方法总结
两个函数图象的交点问题
三角函数的零点(方程根)个数问题
角度三 三角函数图象与性质的综合问题
[例5] (多选)将函数f(x)=2sin -1的图象向左平移个单位长度得到函数g(x)的图象,则下列说法正确的是( )
AC
A.函数g(x)的最小正周期是π
B.函数g(x)的图象关于直线x=-对称
C.函数g(x)在上单调递减
D.函数g(x)在上的最大值是1
g(x)=2sin -1
=2sin-1
函数g(x)的最小正周期T==π
√
当x=-时,函数y=sin没有取得最值,因此g(x)的图象不关于直线x=-对称
×
当x∈时,2x+∈ ,此时函数g(x)单调递减
√
当x∈时,2x+∈,sin∈ ,此时函数g(x)没有最大值
×
方法总结
先将y=f(x)化为y=Asin(ωx+φ)+B的形式,再借助y=Asin(ωx+φ)的图象和性质(如定义域、值域、最值、周期性、对称性、单调性等)解决相关问题.
跟踪训练
(多选)已知函数f(x)=sin ,则下列四个命题中正确的是( )
D.函数y=|f(x)|的图象向左平移个单位长度后所得图象的对称轴方程为x= (k∈Z)
C.函数f(x)在区间上单调递增
B.f(x)= 是x=的充分不必要条件
A.f(x)的最小正周期是π
T= =π
√
由f(x)=得2x-=2kπ+或2x-=2kπ+ (k∈Z),即x=kπ+或x=kπ+(k∈Z),
必要不充分条件
×
由单调递减
×
由y=|sin x|的图象的对称轴为直线x= (k∈Z)得y=|sin 2x|的图象的对称轴为直线x= (k∈Z)
y= =|sin 2x|
√
AD
随堂训练
1.(多选)如图是函数f(x)=Asin(ωx+φ)(ω>0,0<φ<)的部分图象,将函数f(x)的图象向右平移个单位长度得到函数y=g(x)的图象,则下列命题正确的是( )
A.y=g(x)是奇函数
B.函数g(x)的图象的对称轴是直线x=kπ+(k∈Z)
C.函数g(x)的图象的对称中心是(k∈Z)
D.函数g(x)的单调递减区间为(k∈Z)
随堂训练
1.(多选)如图是函数f(x)=Asin(ωx+φ)(ω>0,0<φ<)的部分图象,将函数f(x)的图象向右平移个单位长度得到函数y=g(x)的图象,则下列命题正确的是( )
依题意可得A=2, =+=,故T=π,T= =π,解得ω=2.
f =2sin[2×+φ]=2sin =0,
因为0<φ<,所以φ=,
故f(x)=2sin .
将函数f(x)=2sin的图象向右平移个单位长度得到函数y=g(x)=2sin 2x的图象,
随堂训练
1.(多选)如图是函数f(x)=Asin(ωx+φ)(ω>0,0<φ<)的部分图象,将函数f(x)的图象向右平移个单位长度得到函数y=g(x)的图象,则下列命题正确的是( )
A.y=g(x)是奇函数
B.函数g(x)的图象的对称轴是直线x=kπ+(k∈Z)
C.函数g(x)的图象的对称中心是(k∈Z)
D.函数g(x)的单调递减区间为(k∈Z)
y=g(x)=2sin 2x
√
x= +(k∈Z)
×
(k∈Z)
×
√
AD
2.将函数y=sin x的图象上所有的点向右平移个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是_______________.
向右平移个单位长度
横坐标伸长到原来的2倍(纵坐标不变)
y=sin x
y=sin (x)
y=sin (x)
y=sin (x)
3.函数y=cos(2x+φ)(0<φ<π)的图象向右平移个单位长度后,与函数y=sin的图象重合,则φ=________.
向右平移个单位长度
y=cos(2x+φ)
y=cos (2x-π+φ)
与y=sin的图象重合
cos (2x-π+φ)=sin
sin =sin
-+φ=-
φ=
4.若f(x)=2sin(2x+φ)(φ>0)的图象关于直线x= 对称,且当φ取最小值时, x0∈,使得f(x0)=a,则a的取值范围是_____________.
所以-因为函数f(x)=2sin(2x+φ)(φ>0)的图象关于直线x=对称,
所以+φ=kπ+(k∈Z),
所以φ=kπ+(k∈Z),
又φ>0,所以当φ取最小值时,φ=,f(x)=2sin(2x+) .
因为x0∈,所以2x0+∈ ,
(-,2]
所以函数h(x)的单调递增区间为,k∈Z.
5.将函数f(x)=sin 2x的图象向左平移个单位长度后得到函数g(x)的图象,设函数h(x)=f(x)-g(x).
(1)求函数h(x)的单调递增区间;
(2)若g = ,求h(α)的值.
(1)由已知可得g(x)=sin(2x+) ,
则h(x)=sin 2x-sin(2x+) =sin (2x).
令-+2kπ≤2x-≤+2kπ,k∈Z,得-+kπ≤x≤ +kπ,k∈Z.
5.将函数f(x)=sin 2x的图象向左平移个单位长度后得到函数g(x)的图象,设函数h(x)=f(x)-g(x).
(1)求函数h(x)的单调递增区间;
(2)若g = ,求h(α)的值.
(2)
g=
sin =sin =
sin =-
h(α)=-
本课小结
y=Asin(ωx+φ)的图象、图象变换以及由图象求解析式,尤其是y=Asin(ωx+φ)的图象与性质的综合应用是考查的热点,题型多以选择题为主,难度中等.
函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
考纲分析
课程标准解读 关联考点 核心素养
1.了解函数y=Asin(ωx+φ)的物理意义;能画出y=Asin(ωx+φ)的图象,了解参数A,ω,φ对函数图象变化的影响. 2.了解三角函数是描述周期变化现象的重要函数模型,会利用三角函数模型解决一些简单的实际问题. 1.“五点法”作图及图象变换. 2.求函数y=Asin(ωx+φ)的解析式. 3.三角函数图象与性质的综合问题. 1.直观想象.
2.数学建模.
3.数学运算.
课前自测
(5)若函数y=Asin(ωx+φ)为偶函数,则φ=2kπ+(k∈Z).( )
1.判断正误(正确的打“√”,错误的打“×”)
(1)把y=sin x的图象上各点的横坐标缩短为原来的,纵坐标不变,所得图象对应的函数解析式为y=sin x.( )
×
(2)将y=sin 2x的图象向右平移个单位长度,得到y=sin 的图象.( )
×
(3)函数f(x)=Asin(ωx+φ)(A≠0)的最大值为A,最小值为-A.( )
×
(4)如果y=Acos(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心之间的距离为.( )
√
×
2.为了得到y=3cos 的图象,只需把y=3cos 图象上的所有点的( )
A.纵坐标伸长到原来的3倍,横坐标不变
B.横坐标伸长到原来的3倍,纵坐标不变
C.纵坐标缩短到原来的,横坐标不变
D.横坐标缩短到原来的,纵坐标不变
D
√
3.(易错题)要得到函数y=sin 的图象,只需将函数y=sin 4x的图象( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
y=sin
向左平移个单位长度
y=sin 4x的图象
y=sin 的图象
A
4.若将函数y=2sin 2x的图象向左平移个单位长度,则得到的图象对应的函数表达式为f(x)=_____________.
y=2sin 2x
向左平移个单位长度
f(x)=2sin
=2sin
2sin
5.已知函数f(x)=2sin(ωx+φ) 的部分图象如图所示,则f(x)=_____________.
所以f(x)=2sin (2x-).
设f(x)的最小正周期为T,
根据题图可知, = ,
所以T=π,故ω=2,
根据2sin=0(增区间上的零点)
可知, +φ=2kπ,k∈Z,
即φ=2kπ-,k∈Z,
又|φ|< ,故φ=-.
2sin (2x-)
考点梳理
1.y=Asin(ωx+φ)的有关概念
y=Asin(ωx+φ)(A>0,ω>0),x∈[0,+∞)表示一个振动量时 振幅 周期 频率 相位 初相
A T= f== ωx+φ φ
2.用五点法画y=Asin(ωx+φ)一个周期内的简图
用五点法画y=Asin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示:
x
ωx+φ 0 π 2π
y=Asin(ωx+φ) 0 A 0 -A 0
3. 三角函数图象变换的两种方法(ω>0)
常用结论
(1)对称中心与零点相联系,对称轴与最值点相联系.y=Asin(ωx+φ)的图象有无数条对称轴,可由方程ωx+φ=kπ+(k∈Z)解出;它还有无数个对称中心,即图象与x轴的交点,可由ωx+φ=kπ(k∈Z)解出.
(2)相邻两条对称轴间的距离为,相邻两对称中心间的距离也为,函数的对称轴一定经过图象的最高点或最低点.
常用结论
1
对称中心与零点相联系,对称轴与最值点相联系.y=Asin(ωx+φ)的图象有无数条对称轴,可由方程ωx+φ=kπ+(k∈Z)解出;它还有无数个对称中心,即图象与x轴的交点,可由ωx+φ=kπ(k∈Z)解出.
2
相邻两条对称轴间的距离为,相邻两对称中心间的距离也为,函数的对称轴一定经过图象的最高点或最低点.
常见误区
(2)由y=sin ωx到y=sin(ωx+φ)(ω>0,φ>0)的变换:向左平移个单位长度而非φ个单位长度.
!
(1)函数y=Asin(ωx+φ)+k图象平移的规律:“左加右减,上加下减”.
典例剖析
考点
1
五点法作图及图象变换
[例1] 已知函数f(x)= sin 2x+2cos2x+a,其最大值为2.
(1)求a的值及f(x)的最小正周期;
(2)画出f(x)在[0,π]上的图象.
最小正周期T= =π.
[例1] 已知函数f(x)= sin 2x+2cos2x+a,其最大值为2.
(1)求a的值及f(x)的最小正周期;
f(x)= sin 2x+2cos2x+a
= sin 2x+cos 2x+1+a
=2sin (2x)+1+a
f(x)的最大值为2,
所以a=-1,
[例1] 已知函数f(x)= sin 2x+2cos2x+a,其最大值为2.
(2)画出f(x)在[0,π]上的图象.
x 0 π
2x+ π 2π
f(x)=2sin(2x) 1 2 0 -2 0 1
由(1)知f(x)=2sin (2x) ,列表:
[例1] 已知函数f(x)= sin 2x+2cos2x+a,其最大值为2.
(2)画出f(x)在[0,π]上的图象.
画图如下.
变式探究
1.(变问法)若将本例中函数f(x)的图象向左平移个单位长度,把所有点的横坐标伸长到原来的二倍(纵坐标不变),得到函数g(x)的图象,则g(x)=________________.
由[例1]知f(x)=2sin (2x) ,
向左平移个单位长度
f(x)=2sin [2(x) ]
=2sin (2x)
把所有点的横坐标伸长到原来的二倍(纵坐标不变)
g(x) =2sin (x)
f(x)=2sin (2x)
2sin (x)
2.(变问法)在本例条件下,函数y=2cos 2x的图象向右平移________个单位得到y=f(x)的图象.
由[例1]知f(x)=2sin (2x) ,
向右平移个单位长度
向左平移个单位长度
y=2cos 2x
y=2sin(2x+)
y=2sin 2x
方法总结
函数y=Asin(ωx+φ)(A>0,ω>0的图象的两种作法
五点法 设z=ωx+φ,由z取0,,π,π,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象
图象变 换法 由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)的图象,有两种主要途径“先平移后伸缩”与“先伸缩后平移”
平移变换和伸缩变换都是针对x而言,即x本身加减多少值,而不是ωx加减多少值.
注意
跟踪训练
1.函数y= sin 的图象向左平移φ个单位长度,得到的函数是偶函数,则φ的最小正值是( )
A. B. C. D.
由k=0可得φ的最小正值是.
函数y=sin 向左平移φ个单位长度可得y=sin ,
因为y= sin 是偶函数,
所以2φ+ = +kπ,k∈Z,φ= + ,k∈Z,
A
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
A.f(x)与g(x)的图象重合
B. 为f(x)图象的一个对称中心
C.直线x=-为函数g(x)图象的一条对称轴
D.f(x)的图象向左平移个单位长度可得g(x)的图象
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
①
y=sin x
向左平移个单位长度
y=sin
各点的横坐标缩短到原来的倍
f(x)=sin
②
y=sin x
各点的横坐标缩短到原来的倍
y=sin 2x
向左平移个单位长度
g(x)=sin
=sin
A.f(x)与g(x)的图象重合
×
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
A.f(x)与g(x)的图象重合
×
B. 为f(x)图象的一个对称中心
令2x+ =kπ(k∈Z),得
令k=1,则可知选项B正确;
x=π-(k∈Z),
√
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
A.f(x)与g(x)的图象重合
×
B. 为f(x)图象的一个对称中心
√
C.直线x=-为函数g(x)图象的一条对称轴
令k=-1,则可知选项C正确.
令2x+=kπ +(k∈Z),得x= +(k∈Z),
√
2.(多选)分别对函数y=sin x的图象进行如下变换:①先向左平移个单位长度,然后将其上各点的横坐标缩短到原来的倍,得到y=f(x)的图象;②先将其上各点的横坐标缩短到原来的倍,然后向左平移个单位长度,得到y=g(x)的图象.则以下结论正确的是( )
A.f(x)与g(x)的图象重合
×
B. 为f(x)图象的一个对称中心
√
C.直线x=-为函数g(x)图象的一条对称轴
√
D.f(x)的图象向左平移个单位长度可得g(x)的图象
g(x)=sin=sin[2 ]=f ,
所以f(x)的图象向左平移个单位长度可得g(x)的图象.
√
BCD
考点
2
求y=Asin(ωx+φ)的解析式
[例2] (多选)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)=( )
A.sin B.sin
C.cos D.cos
[例2] (多选)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)=( )
A.sin B.sin
C.cos D.cos
由题图可知,函数的最小正周期T=2=π,
所以=π,ω=±2.
当ω=2时,y=sin(2x+φ),
将点代入得,sin =0,
所以2× +φ=2kπ+π,k∈Z,即φ=2kπ+,k∈Z,
故y=sin.
由于y=sin=sin[π-(2x+)]=sin,故选项B正确;
y=sin(-2x)=cos =cos,选项C正确;
√
√
对于选项A,当x=时, sin=1≠0,错误;
×
[例2] (多选)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)=( )
A.sin B.sin
C.cos D.cos
√
√
×
对于选项D,当x= = 时,cos=1≠-1,错误.
×
当ω=-2时,y=sin(-2x+φ),将代入,得sin(-2×+φ)=0,结合函数图象,知-2×+φ=π+2kπ,k∈Z,得φ=+2kπ,k∈Z,所以y=sin (-2x+) ,但当x=0时,y=sin(-2x+)=-<0,与图象不符合,舍去.
BC
方法总结
②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:
“最大值点”(即图象的“峰点”)时ωx+φ = +2kπ(k∈Z);“最小值点”(即图象的“谷点”)时ωx+φ= +2kπ(k∈Z).
(1)求A,b,确定函数的最大值M和最小值m,
则A= ,b= .
(2)求ω,确定函数的最小正周期T,则可得ω= .
(3)求φ,常用的方法有:
①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上);
确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法
跟踪训练
1.已知函数f(x)=Asin(ωx+φ) 的最小正周期是π,且当x= 时,f(x)取得最大值2,则f(x)=______________.
所以φ= ,所以函数y=f(x)的解析式为f(x)=2sin.
因为函数f(x)的最小正周期是π,所以ω=2.
又因为x=时,f(x)取得最大值2.
所以A=2,
同时2×+φ=2kπ+,k∈Z,
φ=2kπ+,k∈Z,因为-<φ< ,
2sin
2.已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG(点G是图象的最高点)是边长为2的等边三角形,则f(1)=________.
所以f(x)= cos (x+ ),
由题意得,A=,T=4=,ω=.
又因为f(x)=Acos(ωx+φ)为奇函数,
所以φ=+kπ,k∈Z,
由0<φ<π,取k=0,则φ=,
所以f(1)=-.
-
考点
3
函数y=Asin(ωx+φ)图象与性质的综合应用
角度一 三角函数模型的应用
[例3] 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到地面的距离是________米.
当t=40时,f(t)=3-2cos =4(米).
[例3] 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到地面的距离是________米.
以圆心O1为原点,以水平方向为x轴方向,以竖直方向为y轴方向建立平面直角坐标系,
因为大风车的半径为2米,圆上最低点O离地面1米,
12秒旋转一周,
设∠OO1P=θ,运动t秒后与地面的距离为f(t),又周期T=12,
所以θ= ·2π= t,
f(t)=3+2sin =3-2cos t (t≥0),
4
方法总结
需要建立精确的或者数据拟合的模型去解决问题,尤其是利用已知数据建立拟合函数解决实际问题,此类问题体现了数学建模核心素养,考查应用意识.
利用三角函数的有关性质解决问题,其关键是准确理解自变量的意义及自变量与因变量之间的对应法则;
(1)已知函数模型
(2)需要建立函数模型
三角函数模型在实际应用中体现的两个方面
角度二 方程根(函数零点)问题
[例4] 函数y=sin 2x+cos 2x-m在上有两个不同的零点,则m的取值范围是________.
所以y=和y=sin t,t∈的图象有两个不同交点,如图:
函数y=sin 2x+cos 2x-m在上有两个不同的零点,
转化为m=cos 2x+ sin 2x=2sin ,在x∈上有两个不同的实数根.
设2x+=t,则t∈,
所以题目条件可转化为=sin t,在t∈上有两个不同的实数根.
由图象观察知, 的取值范围是,
故m的取值范围是(-2,-1).
角度二 方程根(函数零点)问题
[例4] 函数y=sin 2x+cos 2x-m在上有两个不同的零点,则m的取值范围是_____________.
(-2,-1)
方法总结
两个函数图象的交点问题
三角函数的零点(方程根)个数问题
角度三 三角函数图象与性质的综合问题
[例5] (多选)将函数f(x)=2sin -1的图象向左平移个单位长度得到函数g(x)的图象,则下列说法正确的是( )
AC
A.函数g(x)的最小正周期是π
B.函数g(x)的图象关于直线x=-对称
C.函数g(x)在上单调递减
D.函数g(x)在上的最大值是1
g(x)=2sin -1
=2sin-1
函数g(x)的最小正周期T==π
√
当x=-时,函数y=sin没有取得最值,因此g(x)的图象不关于直线x=-对称
×
当x∈时,2x+∈ ,此时函数g(x)单调递减
√
当x∈时,2x+∈,sin∈ ,此时函数g(x)没有最大值
×
方法总结
先将y=f(x)化为y=Asin(ωx+φ)+B的形式,再借助y=Asin(ωx+φ)的图象和性质(如定义域、值域、最值、周期性、对称性、单调性等)解决相关问题.
跟踪训练
(多选)已知函数f(x)=sin ,则下列四个命题中正确的是( )
D.函数y=|f(x)|的图象向左平移个单位长度后所得图象的对称轴方程为x= (k∈Z)
C.函数f(x)在区间上单调递增
B.f(x)= 是x=的充分不必要条件
A.f(x)的最小正周期是π
T= =π
√
由f(x)=得2x-=2kπ+或2x-=2kπ+ (k∈Z),即x=kπ+或x=kπ+(k∈Z),
必要不充分条件
×
由
×
由y=|sin x|的图象的对称轴为直线x= (k∈Z)得y=|sin 2x|的图象的对称轴为直线x= (k∈Z)
y= =|sin 2x|
√
AD
随堂训练
1.(多选)如图是函数f(x)=Asin(ωx+φ)(ω>0,0<φ<)的部分图象,将函数f(x)的图象向右平移个单位长度得到函数y=g(x)的图象,则下列命题正确的是( )
A.y=g(x)是奇函数
B.函数g(x)的图象的对称轴是直线x=kπ+(k∈Z)
C.函数g(x)的图象的对称中心是(k∈Z)
D.函数g(x)的单调递减区间为(k∈Z)
随堂训练
1.(多选)如图是函数f(x)=Asin(ωx+φ)(ω>0,0<φ<)的部分图象,将函数f(x)的图象向右平移个单位长度得到函数y=g(x)的图象,则下列命题正确的是( )
依题意可得A=2, =+=,故T=π,T= =π,解得ω=2.
f =2sin[2×+φ]=2sin =0,
因为0<φ<,所以φ=,
故f(x)=2sin .
将函数f(x)=2sin的图象向右平移个单位长度得到函数y=g(x)=2sin 2x的图象,
随堂训练
1.(多选)如图是函数f(x)=Asin(ωx+φ)(ω>0,0<φ<)的部分图象,将函数f(x)的图象向右平移个单位长度得到函数y=g(x)的图象,则下列命题正确的是( )
A.y=g(x)是奇函数
B.函数g(x)的图象的对称轴是直线x=kπ+(k∈Z)
C.函数g(x)的图象的对称中心是(k∈Z)
D.函数g(x)的单调递减区间为(k∈Z)
y=g(x)=2sin 2x
√
x= +(k∈Z)
×
(k∈Z)
×
√
AD
2.将函数y=sin x的图象上所有的点向右平移个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是_______________.
向右平移个单位长度
横坐标伸长到原来的2倍(纵坐标不变)
y=sin x
y=sin (x)
y=sin (x)
y=sin (x)
3.函数y=cos(2x+φ)(0<φ<π)的图象向右平移个单位长度后,与函数y=sin的图象重合,则φ=________.
向右平移个单位长度
y=cos(2x+φ)
y=cos (2x-π+φ)
与y=sin的图象重合
cos (2x-π+φ)=sin
sin =sin
-+φ=-
φ=
4.若f(x)=2sin(2x+φ)(φ>0)的图象关于直线x= 对称,且当φ取最小值时, x0∈,使得f(x0)=a,则a的取值范围是_____________.
所以-
所以+φ=kπ+(k∈Z),
所以φ=kπ+(k∈Z),
又φ>0,所以当φ取最小值时,φ=,f(x)=2sin(2x+) .
因为x0∈,所以2x0+∈ ,
(-,2]
所以函数h(x)的单调递增区间为,k∈Z.
5.将函数f(x)=sin 2x的图象向左平移个单位长度后得到函数g(x)的图象,设函数h(x)=f(x)-g(x).
(1)求函数h(x)的单调递增区间;
(2)若g = ,求h(α)的值.
(1)由已知可得g(x)=sin(2x+) ,
则h(x)=sin 2x-sin(2x+) =sin (2x).
令-+2kπ≤2x-≤+2kπ,k∈Z,得-+kπ≤x≤ +kπ,k∈Z.
5.将函数f(x)=sin 2x的图象向左平移个单位长度后得到函数g(x)的图象,设函数h(x)=f(x)-g(x).
(1)求函数h(x)的单调递增区间;
(2)若g = ,求h(α)的值.
(2)
g=
sin =sin =
sin =-
h(α)=-
本课小结
y=Asin(ωx+φ)的图象、图象变换以及由图象求解析式,尤其是y=Asin(ωx+φ)的图象与性质的综合应用是考查的热点,题型多以选择题为主,难度中等.
同课章节目录
