人教版(2019)新教材高中物理必修2 8.4 机械能守恒定律(3)课件(共22张PPT)
文档属性
| 名称 | 人教版(2019)新教材高中物理必修2 8.4 机械能守恒定律(3)课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-11 19:40:27 | ||
图片预览






文档简介
(共22张PPT)
机械能守恒定律
电影《挑战者号》中有一个片段,诺贝尔物理学奖得主,理查德·费曼将一个大铁球挂在铁链上做成单摆,演示了机械能的守恒。
伽利略斜面实验
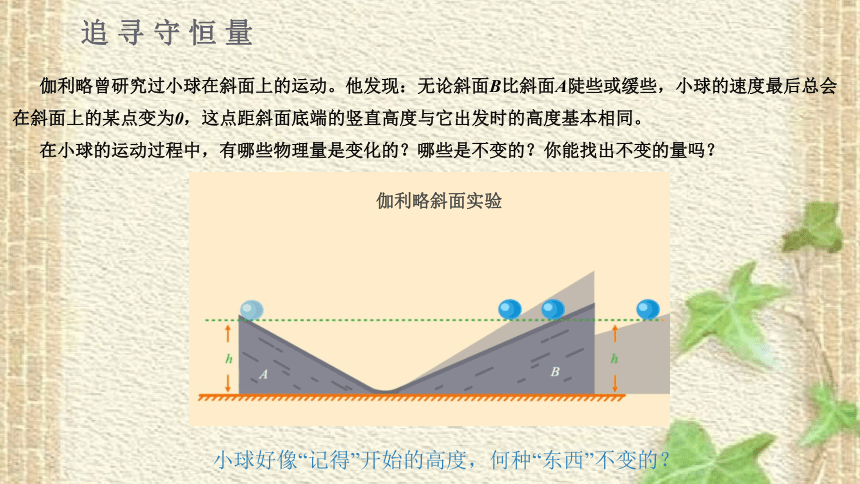
追 寻 守 恒 量
小球好像“记得”开始的高度,何种“东西”不变的?
伽利略曾研究过小球在斜面上的运动。他发现:无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0,这点距斜面底端的竖直高度与它出发时的高度基本相同。
在小球的运动过程中,有哪些物理量是变化的?哪些是不变的?你能找出不变的量吗?
能量角度:
下滑时重力势能减少,动能增加;
上滑时重力势能增加,动能减少。
追 寻 守 恒 量
科学方法:
采用理想实验法,其核心是“可靠的
事实”+“严密的逻辑推理”。
理想斜面实验
动能与重力势能的相互转化
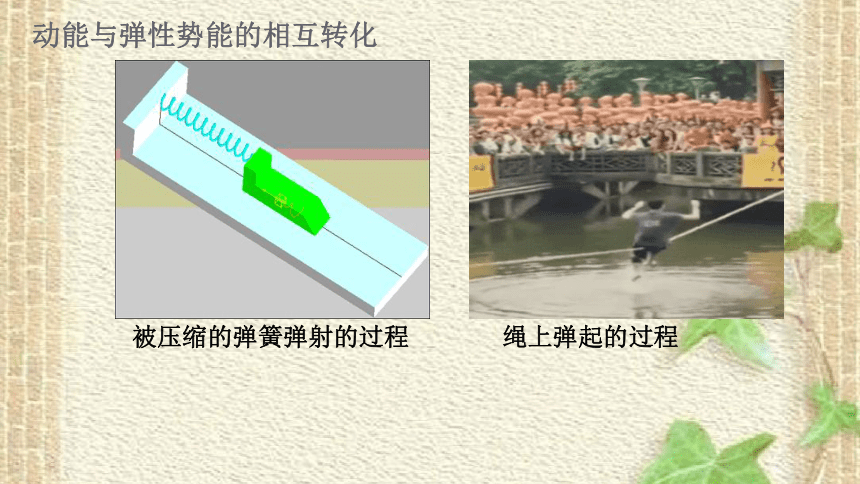
被压缩的弹簧弹射的过程
绳上弹起的过程
动能与弹性势能的相互转化
1.重力势能、弹性势能与动能都是机械运动中的能量形式——机械能。
2.通过重力或弹力做功,机械能可以从一种形式转化为另一种形式。
动能与势能的相互转化
动 能 与 势 能 的 相 互 转 化
是 否 存 在 某 种 定 量 的 关 系 ?
公 式 推 导
情景1
1.举例推导
动能定理:
功能关系:
光滑曲面
联立变形:
【结论】只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
x
原长 2 1
光滑平面
2.举例推导
动能定理:
功能关系:
联立变形:
【结论】只有弹力做功的系统内,动能与弹性势能互相转化时总的机械能保持不变。
情景2
公 式 推 导
定律理解
在只有重力或弹力做功的物体系统内,动能和势能可以互相转化,而总的机械能保持不变。
4.内容
只有弹力做功的系统内
忽略阻力,只有重力做功
3.总结归纳
需要设定零势能面
定律理解
定律理解
判断下图中系统及单个物体的机械能是否守恒?
定律理解
【例1】 如图所示,下列关于机械能是否守恒的判断正确的是( )
A.甲图中,物体A将弹簧压缩的过程中,物体A的机械能守恒
B.乙图中,物体B在大小等于摩擦力的拉力作用下沿斜面下滑时,机械能守恒
C.丙图中,不计任何阻力时A加速下落、B加速上升的过程中,A、B组成的系统机械能守恒
D.丁图中,不计空气阻力,小球由水平位置A处静止释放,运动到B处的过程中,机械能守恒
BCD
A与弹簧组成的系统机械能才守恒
只有重力做功,其他力做功代数和为0
AB组成的额系统内,只有动能与势能转化
小球所受的拉力不做功,只有重力做功
定 律 理 解
机械能守恒定律的应用
1.机械能守恒定律常用的三种表达式
(1)从不同状态看:Ek1+Ep1=Ek2+Ep2(或E1=E2)
此式表示系统两个状态的机械能总量相等.
(2)从能的转化角度看:ΔEk=-ΔEp
此式表示系统动能的增加(减少)量等于势能的减少(增加)量.
(3)从能的转移角度看:ΔEA增=ΔEB减
此式表示系统A部分机械能的增加量等于系统剩余部分,即B部分机械能的减少量.
定 律 理 解
2.应用机械能守恒定律解题的一般步骤
(1)根据题意选取研究对象;
(2)明确研究对象的运动过程,分析研究对象在此过程中的受力情况,弄清各力做功的情况,判断机械能是否守恒.
(3)恰当地选取参考平面,确定研究对象在此过程中的初态和末态的机械能.
(4)根据机械能守恒定律的不同表达式列方程并求解.
【例2】 如图所示,把一个小球用细线悬挂起来,就成为一个摆,摆长为l,最大偏角为θ。如果阻力可以忽略,小球运动到最低点时的速度大小是多少?
【解】以小球为研究对象。设最低点O的重力势能为0,以小球最高点的状态作为初状态,以小球最低点的状态作为末状态。
初状态的机械能:
末状态的机械能:
由机械能守恒定律得:
需要设定零势能面
得所求的速度大小:
【例3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
【动力学方法】
【动能定理】
【机械能守恒定律】
① 隔离法:
对A: T-mg=ma
对B: 3mg-T=3ma
联立得: T=1.5mg
② 根据牛顿第二定律求出A球的加速度a=g/2
③ 根据运动学公式求解A球速度v
① 由连接体问题的思路求出绳上的拉力:T=1.5mg
② 根据动能定理分析A球:
(T-mg)h=mv2/2
根据系统机械能守恒:
3mgh=mgh+mv2/2+3mv2/2
随堂演练
1.关于机械能守恒的叙述,下列说法正确的是
A.做匀速圆周运动的物体,机械能一定守恒
B.物体所受的合力不等于零,机械能可能守恒
C.物体做匀速直线运动,机械能一定守恒
D.物体所受合力做功为零,机械能一定守恒
2.如图9是一个设计“过山车”的试验装置的原理示意图,斜面AB与竖直面内的圆形轨道在B点平滑连接,斜面AB和圆形轨道都是光滑的,圆形轨道半径为R,一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,小车恰能通过圆形轨道的最高点C.已知重力加速度为g.求:
(1)A点距水平面的高度h;
(2)运动到B点时小车对圆形轨道压力的大小.
由A运动到C,设地面的重力势能为0, 根据机械能守恒定律得:
解得:h=2.5R
解得:FN=6mg
由牛顿第三定律可知,运动到B点时小车对圆形轨道的压力大小为6mg.
机械能守恒定律
电影《挑战者号》中有一个片段,诺贝尔物理学奖得主,理查德·费曼将一个大铁球挂在铁链上做成单摆,演示了机械能的守恒。
伽利略斜面实验
追 寻 守 恒 量
小球好像“记得”开始的高度,何种“东西”不变的?
伽利略曾研究过小球在斜面上的运动。他发现:无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0,这点距斜面底端的竖直高度与它出发时的高度基本相同。
在小球的运动过程中,有哪些物理量是变化的?哪些是不变的?你能找出不变的量吗?
能量角度:
下滑时重力势能减少,动能增加;
上滑时重力势能增加,动能减少。
追 寻 守 恒 量
科学方法:
采用理想实验法,其核心是“可靠的
事实”+“严密的逻辑推理”。
理想斜面实验
动能与重力势能的相互转化
被压缩的弹簧弹射的过程
绳上弹起的过程
动能与弹性势能的相互转化
1.重力势能、弹性势能与动能都是机械运动中的能量形式——机械能。
2.通过重力或弹力做功,机械能可以从一种形式转化为另一种形式。
动能与势能的相互转化
动 能 与 势 能 的 相 互 转 化
是 否 存 在 某 种 定 量 的 关 系 ?
公 式 推 导
情景1
1.举例推导
动能定理:
功能关系:
光滑曲面
联立变形:
【结论】只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
x
原长 2 1
光滑平面
2.举例推导
动能定理:
功能关系:
联立变形:
【结论】只有弹力做功的系统内,动能与弹性势能互相转化时总的机械能保持不变。
情景2
公 式 推 导
定律理解
在只有重力或弹力做功的物体系统内,动能和势能可以互相转化,而总的机械能保持不变。
4.内容
只有弹力做功的系统内
忽略阻力,只有重力做功
3.总结归纳
需要设定零势能面
定律理解
定律理解
判断下图中系统及单个物体的机械能是否守恒?
定律理解
【例1】 如图所示,下列关于机械能是否守恒的判断正确的是( )
A.甲图中,物体A将弹簧压缩的过程中,物体A的机械能守恒
B.乙图中,物体B在大小等于摩擦力的拉力作用下沿斜面下滑时,机械能守恒
C.丙图中,不计任何阻力时A加速下落、B加速上升的过程中,A、B组成的系统机械能守恒
D.丁图中,不计空气阻力,小球由水平位置A处静止释放,运动到B处的过程中,机械能守恒
BCD
A与弹簧组成的系统机械能才守恒
只有重力做功,其他力做功代数和为0
AB组成的额系统内,只有动能与势能转化
小球所受的拉力不做功,只有重力做功
定 律 理 解
机械能守恒定律的应用
1.机械能守恒定律常用的三种表达式
(1)从不同状态看:Ek1+Ep1=Ek2+Ep2(或E1=E2)
此式表示系统两个状态的机械能总量相等.
(2)从能的转化角度看:ΔEk=-ΔEp
此式表示系统动能的增加(减少)量等于势能的减少(增加)量.
(3)从能的转移角度看:ΔEA增=ΔEB减
此式表示系统A部分机械能的增加量等于系统剩余部分,即B部分机械能的减少量.
定 律 理 解
2.应用机械能守恒定律解题的一般步骤
(1)根据题意选取研究对象;
(2)明确研究对象的运动过程,分析研究对象在此过程中的受力情况,弄清各力做功的情况,判断机械能是否守恒.
(3)恰当地选取参考平面,确定研究对象在此过程中的初态和末态的机械能.
(4)根据机械能守恒定律的不同表达式列方程并求解.
【例2】 如图所示,把一个小球用细线悬挂起来,就成为一个摆,摆长为l,最大偏角为θ。如果阻力可以忽略,小球运动到最低点时的速度大小是多少?
【解】以小球为研究对象。设最低点O的重力势能为0,以小球最高点的状态作为初状态,以小球最低点的状态作为末状态。
初状态的机械能:
末状态的机械能:
由机械能守恒定律得:
需要设定零势能面
得所求的速度大小:
【例3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
【动力学方法】
【动能定理】
【机械能守恒定律】
① 隔离法:
对A: T-mg=ma
对B: 3mg-T=3ma
联立得: T=1.5mg
② 根据牛顿第二定律求出A球的加速度a=g/2
③ 根据运动学公式求解A球速度v
① 由连接体问题的思路求出绳上的拉力:T=1.5mg
② 根据动能定理分析A球:
(T-mg)h=mv2/2
根据系统机械能守恒:
3mgh=mgh+mv2/2+3mv2/2
随堂演练
1.关于机械能守恒的叙述,下列说法正确的是
A.做匀速圆周运动的物体,机械能一定守恒
B.物体所受的合力不等于零,机械能可能守恒
C.物体做匀速直线运动,机械能一定守恒
D.物体所受合力做功为零,机械能一定守恒
2.如图9是一个设计“过山车”的试验装置的原理示意图,斜面AB与竖直面内的圆形轨道在B点平滑连接,斜面AB和圆形轨道都是光滑的,圆形轨道半径为R,一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,小车恰能通过圆形轨道的最高点C.已知重力加速度为g.求:
(1)A点距水平面的高度h;
(2)运动到B点时小车对圆形轨道压力的大小.
由A运动到C,设地面的重力势能为0, 根据机械能守恒定律得:
解得:h=2.5R
解得:FN=6mg
由牛顿第三定律可知,运动到B点时小车对圆形轨道的压力大小为6mg.
