第5单元完美的图形-圆易错题检测卷-小学数学六年级上册青岛版
文档属性
| 名称 | 第5单元完美的图形-圆易错题检测卷-小学数学六年级上册青岛版 |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 10:27:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
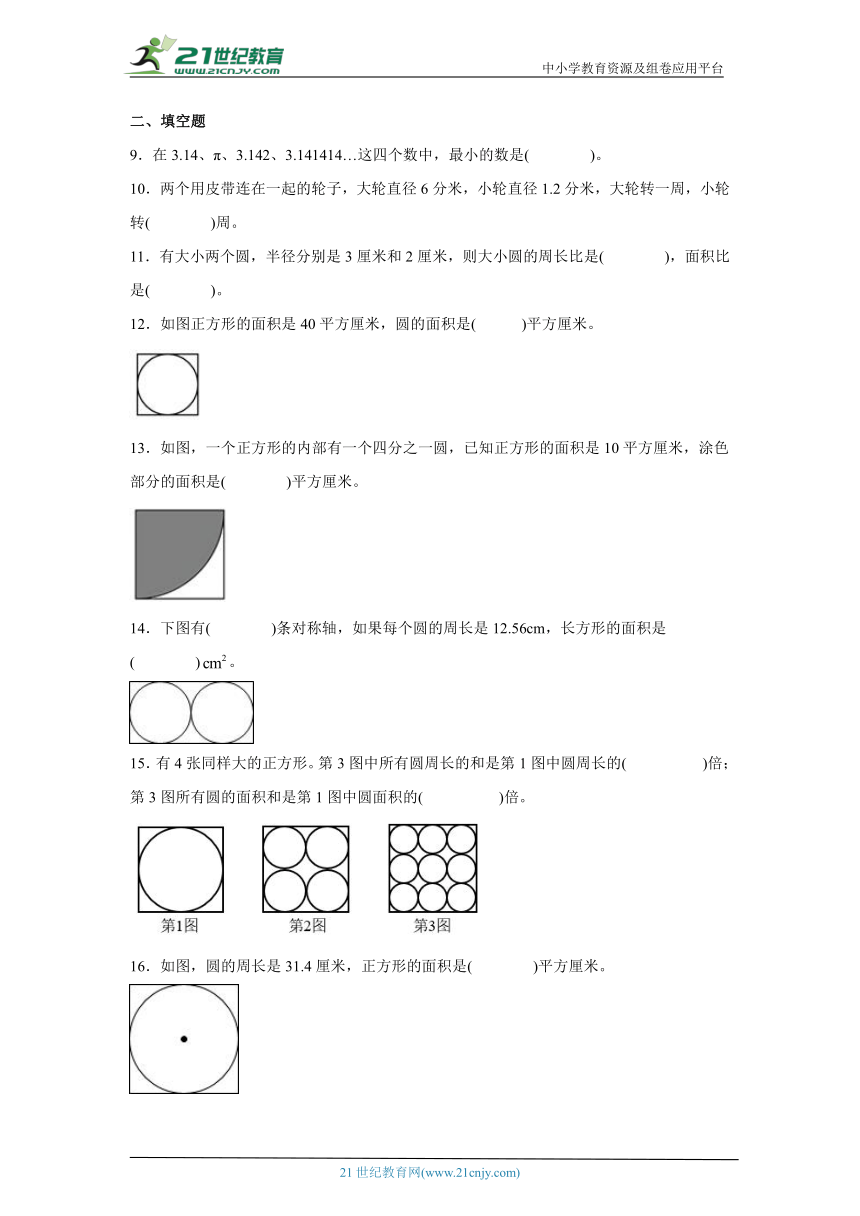
第5单元完美的图形-圆检测卷-小学数学六年级上册青岛版
一、选择题
1.一个半圆,它的半径是r,这个半圆的周长是( )。
A.πr B.πr+2r C.2πr+2r D.2πr
2.1张圆形纸片至少对折( )次,才能找到圆心。
A.1 B.2 C.3 D.0
3.车轮滚动一周,所行的路程就是车轮的( )。
A.直径 B.周长 C.面积 D.体积
4.从一个半径为0.5厘米的圆上取一点,在直线上从“0”开始滚动一周后,这个点的位置大约是( )。21教育名师原创作品
A. B.
C. D.
5.下面的阴影部分是扇形的是( )。
A. B. C.
6.有大小两个圆,大圆半径是5厘米,小圆半径是4厘米,小圆面积是大圆面积的( )。
A. B. C.
7.下图是3个相同的圆,半径都是2cm,连接3个圆心,阴影面积是( )。
A. B. C.答案A、B都不对
8.用一根铁丝围成一个半径8cm的圆,用它来围成一个正方形,它的边长是( )。
A.12.56cm B.20.12cm C.10.06cm
二、填空题
9.在3.14、π、3.142、3.141414…这四个数中,最小的数是( )。
10.两个用皮带连在一起的轮子,大轮直径6分米,小轮直径1.2分米,大轮转一周,小轮转( )周。21教育网
11.有大小两个圆,半径分别是3厘米和2厘米,则大小圆的周长比是( ),面积比是( )。21*cnjy*com
12.如图正方形的面积是40平方厘米,圆的面积是( )平方厘米。
13.如图,一个正方形的内部有一个四分之一圆,已知正方形的面积是10平方厘米,涂色部分的面积是( )平方厘米。
14.下图有( )条对称轴,如果每个圆的周长是12.56cm,长方形的面积是( )。
15.有4张同样大的正方形。第3图中所有圆周长的和是第1图中圆周长的( )倍;第3图所有圆的面积和是第1图中圆面积的( )倍。
16.如图,圆的周长是31.4厘米,正方形的面积是( )平方厘米。
三、判断题
17.用4个半径相等且圆心角都是90°的扇形一定可以拼成一个圆。( )
18.一个圆的直径增加1倍后,它的面积是原来的4倍。( )
19.半圆的周长等于圆周长的一半。( )
20.直径为4厘米的圆的面积等于两个直径为2厘米的圆的面积之和。( )
21.圆中的任一条直径都是它的对称轴。( )
四、图形计算
22.求图中阴影部分的周长和面积。
23.求阴影部分面积。
五、解答题
24.青岛电视塔的塔蝶直径为32米,塔蝶之上的环形露天观光平台的宽度是4.5米。环形露天观光平台的面积是多少?【出处:21教育名师】
25.一个圆形花坛原来直径是24米,扩建后的直径与原来的比是4∶3,扩建后花坛的面积增加了多少平方米?
26.明明用一根30米长的绳子测一棵树干的直径,在树干上绕了10圈绳子还剩余1.74米。
27.有一张圆桌,直径是12分米。现在要给这张圆桌配上一块桌布,圆桌铺上桌布后,四周要均匀垂下3分米,这块桌布的面积是多少平方分米?
28.在花卉博览会上,把一个直径为10米的圆形展区的半径向外延伸2米变成一个新的圆形展区(如图)。
(1)新展区的面积比原来增加了多少平方米?
(2)新展区圆周外围每隔3.14米安装1盏装饰灯,需要多少盏装饰灯?
29.一辆小汽车轮胎的外直径是100厘米。在行驶中平均每分钟转300圈,照这样计算,这辆小汽车半小时行驶多少千米?(结果保留整数)
参考答案:
1.B
【分析】周长是指封闭图形一周的长度。半圆的周长等于该圆周长的一半加上一条直径的长度,根据圆的周长公式C=2πr,圆的直径d=2r,据此解答。
【详解】2πr÷2+d=πr+2r
一个半圆,它的半径是r,这个半圆的周长是πr+2r。
故答案为:B
【点睛】理解掌握周长的意义及半圆周长公式,明确半圆的周长是由哪几部分组成是解题的关键。
2.B
【分析】圆形纸片对折1次,折痕是圆内最长的线段,就是圆的直径。再对折一次,展开后两条折痕的交点就是圆心。2·1·c·n·j·y
【详解】1张圆形纸片至少对折2次,才能找到圆心。
故答案为:B。
【点睛】本题主要考查圆的特征,也可以通过动手实践来解题。
3.B
【分析】车轮滚动一周,所行的路程就是这个车轮的周长,可采用化曲为直的方法进行计算。
【详解】由分析可知:
车轮滚动一周,所行的路程就是车轮的周长。
故答案为:B
【点睛】此题主要考查的是利用圆的周长求车轮的所行路程。
4.C
【分析】由题干可知,求的是半径为0.5厘米的圆的周长,根据圆的周长公式C=2πr即可解答。
【详解】2×3.14×0.5
=6.28×0.5
=3.14(厘米)
3<3.14<4
故选:C
【点睛】此题考查的是圆的周长的应用,灵活运用公式是解题关键。
5.A
【分析】圆上一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,据此判断即可。
【详解】由分析可知,阴影部分是扇形的是。
故答案为:A
【点睛】解答本题关键是深刻理解扇形的意义。
6.B
【分析】根据圆的面积公式:π×半径2,求出大圆面积和小圆面积,再用小圆面积除以大圆面积,即可解答。
【详解】大圆面积:π×52=25π(平方厘米)
小圆面积:π×42=16π(平方厘米)
16π÷25π=
故答案为:B
【点睛】本题考查圆的面积公式的应用,以及求一个数是另一个数的几分之几。
7.B
【分析】观察图形可知,3个圆的圆心连接是一个等边三角形,根据等边三角形的特征,三个内角相等,都等于60°;阴影部分面积是3个圆心角为60°的扇形面积和;60°×3=180°,阴影部分面积就是半径为2cm圆的面积的一半,根据圆的面积公式:π×半径2,代入数据,求出一个圆的面积,再除以2,就是这个阴影部分的面积。21cnjy.com
【详解】3.14×22÷2
=3.14×4÷2
=12.56÷2
=6.28(cm2)
故答案选:B
【点睛】本题考查等边三角形的特征,圆的面积公式的应用,解答本题的关键是明确阴影部分面积等于半径为2cm圆的面积的一半。2-1-c-n-j-y
8.A
【分析】由于铁丝围成一个圆,再围成一个正方形, 则圆和正方形的周长相等,根据圆的周长公式:C=2πr,求出铁丝的长度,再根据正方形的周长公式:边长×4,把数代入即可求解。
【详解】3.14×2×8
=6.28×8
=50.24(厘米)
50.24÷4=12.56(厘米)
故答案为:A
【点睛】本题主要考查正方形和圆的周长公式,熟练掌握它们的公式并灵活运用。
9.3.14
【分析】先明确π=3.1415926…,然后按照小数比较大小的方法,先比较小数的整数部分,如果整数部分相同,再比较小数的十分位,如果十分位也相同,再比较小数的百分位……以此比较即可。
【详解】π=3.1415926…
3.14<3.141414…<π<3.142
所以在3.14,π,3.142,3.141414…这四个数中,最小的数是3.14。
【点睛】本题考查了小数比较大小的方法,按照小数比较大小的方法,先比较小数的整数部分,如果整数部分相同,再比较小数的十分位,如果十分位也相同,再比较小数的百分位……以此比较即可。
10.5
【分析】根据圆的周长公式分别求出大轮和小轮的周长,再用大轮的周长除以小轮的周长,求出大轮转1周,小轮要转多少周即可。
【详解】3.14×6÷(3.14×1.2)
=18.84÷3.768
=5(周)
【点睛】本题考查了圆周长的应用,灵活运用圆的周长公式是解题的关键。
11. 3∶2 9∶4
【分析】根据圆的周长公式:C=2πr,圆的面积公式:S=πr2,因为圆周率是一定,所以圆的周长与半径成正比例,也就是大小圆的周长的比等于大小圆半径的比,大小圆面积的比等于大小圆半径平方的比;据此解答即可。【来源:21cnj*y.co*m】
【详解】因为大小圆半径的比是3∶2,所以大小圆周长的比是3∶2
大小圆面积的比是32∶22=9∶4。
【点睛】此题主要考查圆的周长公式、面积公式的灵活运用,比的意义及应用,关键是熟记公式。
12.31.4
【分析】根据正方形面积公式:正方形面积=边长×边长;观察图形可知,正方形的边长等于圆的直径,正方形面积=4×半径×半径,半径×半径=40÷4=10;根据圆的面积=π×半径×半径,即圆的面积=π×(正方形面积÷4),代入数据,即可解答。【版权所有:21教育】
【详解】3.14×(40÷4)
=3.14×10
=31.4(平方厘米)
【点睛】解答此题的关键是理解正方形的边长等于圆的直径,半径的平方=正方形面积÷4。
13.7.85
【分析】正方形的面积是边长的平方,又知正方形面积是10平方厘米,即正方形边长2=10平方厘米,正方形的边长又是这个圆的半径,即r2=10平方厘米,根据圆的面积S=πr2,即可求出这个圆的面积,进而求出这个圆的面积。
【详解】3.14×10×
=31.4×
=7.85(平方厘米)
【点睛】本题是考查阴影部分的面积,解答此题的关键是明确正方形的面积就是这个圆的半径的平方。
14. 2 32
【分析】通过观察图形可知,这个图形有2条对称轴,根据圆的周长公式:C=πd,那么d=C÷π,据此求出圆的直径,长方形的长等于直径的2倍,长方形的宽等于直径,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】由图可知,这个图形有2条对称轴,
12.56÷3.14=4(cm)
4×2×4
=8×4
=32(cm2)
【点睛】此题考查的目的是理解掌握轴对称图形的特征及应用,圆的周长公式、长方形的面积公式及应用,关键是熟记公式。
15. 3 1
【分析】假设出正方形的边长,第1图中圆的半径是边长的,第3图中每个圆的半径是正方形边长的,根据“”“”求出圆的周长和面积,最后用除法计算出它们的倍数关系,据此解答。
【详解】假设正方形边长为1厘米,第1图中圆的半径为厘米,直径为×2=1厘米,第3图中圆的半径为厘米,直径为×2=厘米。
第1图圆的周长:×1=(厘米)
第3图圆的周长:××9=3(厘米)
3÷=3
所以,第3图中所有圆周长的和是第1图中圆周长的3倍。
第1图圆的面积:×()2=(平方厘米)
第3图圆的面积:×()2×9
=××9
=(平方厘米)
÷=1
所以,第3图所有圆的面积和是第1图中圆面积的1倍。
【点睛】掌握圆的周长和面积的计算公式是解答题目的关键。
16.100
【分析】观察图形可知,圆的直径相当于正方形边长,根据圆的周长公式:C=πd,据此求出正方形的边长,再根据正方形的面积=边长×边长,据此解答即可。
【详解】31.4÷3.14=10(厘米)
10×10=100(平方厘米)
【点睛】本题考查圆的周长,明确圆的直径相当于正方形的边长是解题的关键。
17.√
【分析】半径决定圆的大小,一个整圆的圆心角是360°,所以用4个半径相等且圆心角是90°的扇形可以拼成一个圆。据此判断即可。【来源:21·世纪·教育·网】
【详解】由分析可知:
因为4个扇形的半径相等,且圆心角都是90°,所以可以拼成一个圆。原题干说法正确。
故答案为:√
【点睛】本题考查扇形和圆心角,明确半径决定圆的大小是解题的关键。
18.√
【分析】根据题意,设圆的直径为d,增加1倍后的直径为2d,根据圆的面积公式可分别计算出直径增加前和增加后圆的面积,然后再用增加后的面积除以原来的面积即可。
【详解】设圆的直径为d,圆的半径为,增加1倍后的直径为2d,圆的半径为d
原来的面积为:π()2
增加后的面积为:πd2
所以πd2÷π()2=4
【点睛】本题考查了圆的面积知识,完成本题要在了解圆的面积公式的基础上进行。
19.×
【分析】半圆的周长应是圆周长的一半再加一条直径,据此判断即可。
【详解】半圆的周长不等于圆周长的一半,还需要再加上一条直径,原题说法错误;
故答案为:×。
【点睛】明确半圆周长的含义是解答本题的关键。
20.×
【分析】根据圆的面积公式S=,代入数据判断即可。
【详解】
=3.14×4
=12.56(平方厘米)
=3.14×1×2
=6.28(平方厘米)
12.56>6.28
故答案为:×
【点睛】本题考查了圆的面积的计算方法,应理解掌握,灵活运用。
21.×
【分析】依据轴对称图形的定义:一个圆形沿一条直径所在的直线对折,对折后的两部分都能完全重合,所以,任一条直径所在的直线都是它的对称轴。即可作答。
【详解】沿圆的每一条直径所在的直线对折,对折后的两部分都能完全重合,所以,任一条直径所在的直线都是它的对称轴,因此圆的直径不是其对称轴,圆的直径所在的直线是其对称轴。21*cnjy*com
故答案为:×
【点睛】解答此题的关键是明白对称轴是直线,而圆的直径是线段。
22.周长:35.7厘米;
面积:21.5平方厘米
【分析】观察图形可知,阴影部分的周长=半径为10厘米圆周长的+2个半径的长度;阴影部分的面积=边长为10厘米的正方形的面积-半径为10厘米圆面积的;据此即可解答问题。
【详解】周长:
3.14×10×2×+10×2
=15.7+20
=35.7(厘米)
面积:
10×10-10×10×3.14×
=100-78.5
=21.5(平方厘米)
23.251.2平方厘米
【分析】阴影部分是一个圆环,圆环的面积=π(R2-r2),据此解答。
【详解】3.14×(122-82)
=3.14×(144-64)
=3.14×80
=251.2(平方厘米)
24.388.575平方米
【分析】先利用塔蝶直径求出外圆的半径,减去环宽4.5米,就是内圆的半径,再利用圆环的面积公式:即可求出环形露天观光平台的面积。
【详解】32÷2=16(米)
16-4.5=11.5(米)
=
=
=(平方米)
答:环形露天观光平台的面积是388.575平方米。
【点睛】此题的解题关键是掌握圆环的面积的计算方法。
25.351.68平方米
【分析】一个圆形花坛,原来直径是24米,扩建后的直径与原来直径的比是4:3,则原来的直径是扩建后的,用除法即可求出扩建后的直径;根据圆的面积公式分别求出扩建前和扩建后花坛的面积,进而求出增加了多少。www.21-cn-jy.com
【详解】24÷=32(米)
3.14×(32÷2) -3.14×(24÷2)
=3.14×16 -3.14×12
=3.14×256-3.14×144
=803.84-452.16
=351.68(平方米)
答:扩建后花坛的面积增加了351.68平方米。
【点睛】解答此题的关键本是根据比与分数的关系,知道原来的直径是扩建后的直径几分之几,求出扩建后的直径,进而求出扩建后花坛的面积与原来相差多少。
26.0.9米
【分析】求绳子的长度减去剩余的的绳子长,除以10圈,得到一圈的长度,利用圆的周长,求出树干的直径。21·cn·jy·com
【详解】
(米)
答:这棵树干的直径大约是0.9米。
【点睛】此题的解题关键是利用圆的周长公式,求出正确的答案。
27.254.34平方分米
【分析】由题意可知:桌布的直径比圆桌的直径长3+3=6分米,由此得出桌布的直径,带入圆的面积公式即可求出桌布的面积。21·世纪*教育网
【详解】12+3+3=18(分米)
3.14×(18÷2)2
=3.14×81
=254.34(平方分米)
答:这块桌布的面积是254.34平方分米。
【点睛】本题主要考查圆的面积公式的实际应用,求出桌布的直径是解题的关键。
28.(1)75.36平方米;
(2)14盏
【分析】(1)依据圆的面积公式,先求出扩宽后大圆的面积;接下来用大圆面积减去小圆面积,即可求出圆环面积;21世纪教育网版权所有
(2)根据在封闭图形上的植树问题,栽树的棵数=间隔数,用新展区圆周外围周长除以3.14求得一共需要安装多少盏装饰灯。
【详解】(1)10÷2=5(米)
3.14×(5+2)2-3.14×52
=3.14×49-3.14×25
=3.14×(49-25)
=3.14×24
=75.36(平方米)
答:新展区的面积比原来增加了75.36平方米。
(2)3.14×(10+2+2)÷3.14
=3.14×14÷3.14
=14(盏)
答:需要14盏装饰灯。
【点睛】本题考查了圆环面积的计算以及在封闭图形上的植树问题,知识点是:“环形的面积=大圆的面积-小圆的面积”,“栽树的棵数=间隔数”。www-2-1-cnjy-com
29.28千米
【分析】由题意知:先求得轮胎的周长,再乘300圈,得一分钟卡车行驶的距离,再乘30,得半小时行驶的距离。据此解答。
【详解】3.14×100×300×30
=314×300×30
=94200×30
=2826000(厘米)
≈28千米
答:这辆小汽车半小时行驶约28千米。
【点睛】本题考查了圆周长公式的运用。求得轮能胎的周长是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第5单元完美的图形-圆检测卷-小学数学六年级上册青岛版
一、选择题
1.一个半圆,它的半径是r,这个半圆的周长是( )。
A.πr B.πr+2r C.2πr+2r D.2πr
2.1张圆形纸片至少对折( )次,才能找到圆心。
A.1 B.2 C.3 D.0
3.车轮滚动一周,所行的路程就是车轮的( )。
A.直径 B.周长 C.面积 D.体积
4.从一个半径为0.5厘米的圆上取一点,在直线上从“0”开始滚动一周后,这个点的位置大约是( )。21教育名师原创作品
A. B.
C. D.
5.下面的阴影部分是扇形的是( )。
A. B. C.
6.有大小两个圆,大圆半径是5厘米,小圆半径是4厘米,小圆面积是大圆面积的( )。
A. B. C.
7.下图是3个相同的圆,半径都是2cm,连接3个圆心,阴影面积是( )。
A. B. C.答案A、B都不对
8.用一根铁丝围成一个半径8cm的圆,用它来围成一个正方形,它的边长是( )。
A.12.56cm B.20.12cm C.10.06cm
二、填空题
9.在3.14、π、3.142、3.141414…这四个数中,最小的数是( )。
10.两个用皮带连在一起的轮子,大轮直径6分米,小轮直径1.2分米,大轮转一周,小轮转( )周。21教育网
11.有大小两个圆,半径分别是3厘米和2厘米,则大小圆的周长比是( ),面积比是( )。21*cnjy*com
12.如图正方形的面积是40平方厘米,圆的面积是( )平方厘米。
13.如图,一个正方形的内部有一个四分之一圆,已知正方形的面积是10平方厘米,涂色部分的面积是( )平方厘米。
14.下图有( )条对称轴,如果每个圆的周长是12.56cm,长方形的面积是( )。
15.有4张同样大的正方形。第3图中所有圆周长的和是第1图中圆周长的( )倍;第3图所有圆的面积和是第1图中圆面积的( )倍。
16.如图,圆的周长是31.4厘米,正方形的面积是( )平方厘米。
三、判断题
17.用4个半径相等且圆心角都是90°的扇形一定可以拼成一个圆。( )
18.一个圆的直径增加1倍后,它的面积是原来的4倍。( )
19.半圆的周长等于圆周长的一半。( )
20.直径为4厘米的圆的面积等于两个直径为2厘米的圆的面积之和。( )
21.圆中的任一条直径都是它的对称轴。( )
四、图形计算
22.求图中阴影部分的周长和面积。
23.求阴影部分面积。
五、解答题
24.青岛电视塔的塔蝶直径为32米,塔蝶之上的环形露天观光平台的宽度是4.5米。环形露天观光平台的面积是多少?【出处:21教育名师】
25.一个圆形花坛原来直径是24米,扩建后的直径与原来的比是4∶3,扩建后花坛的面积增加了多少平方米?
26.明明用一根30米长的绳子测一棵树干的直径,在树干上绕了10圈绳子还剩余1.74米。
27.有一张圆桌,直径是12分米。现在要给这张圆桌配上一块桌布,圆桌铺上桌布后,四周要均匀垂下3分米,这块桌布的面积是多少平方分米?
28.在花卉博览会上,把一个直径为10米的圆形展区的半径向外延伸2米变成一个新的圆形展区(如图)。
(1)新展区的面积比原来增加了多少平方米?
(2)新展区圆周外围每隔3.14米安装1盏装饰灯,需要多少盏装饰灯?
29.一辆小汽车轮胎的外直径是100厘米。在行驶中平均每分钟转300圈,照这样计算,这辆小汽车半小时行驶多少千米?(结果保留整数)
参考答案:
1.B
【分析】周长是指封闭图形一周的长度。半圆的周长等于该圆周长的一半加上一条直径的长度,根据圆的周长公式C=2πr,圆的直径d=2r,据此解答。
【详解】2πr÷2+d=πr+2r
一个半圆,它的半径是r,这个半圆的周长是πr+2r。
故答案为:B
【点睛】理解掌握周长的意义及半圆周长公式,明确半圆的周长是由哪几部分组成是解题的关键。
2.B
【分析】圆形纸片对折1次,折痕是圆内最长的线段,就是圆的直径。再对折一次,展开后两条折痕的交点就是圆心。2·1·c·n·j·y
【详解】1张圆形纸片至少对折2次,才能找到圆心。
故答案为:B。
【点睛】本题主要考查圆的特征,也可以通过动手实践来解题。
3.B
【分析】车轮滚动一周,所行的路程就是这个车轮的周长,可采用化曲为直的方法进行计算。
【详解】由分析可知:
车轮滚动一周,所行的路程就是车轮的周长。
故答案为:B
【点睛】此题主要考查的是利用圆的周长求车轮的所行路程。
4.C
【分析】由题干可知,求的是半径为0.5厘米的圆的周长,根据圆的周长公式C=2πr即可解答。
【详解】2×3.14×0.5
=6.28×0.5
=3.14(厘米)
3<3.14<4
故选:C
【点睛】此题考查的是圆的周长的应用,灵活运用公式是解题关键。
5.A
【分析】圆上一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,据此判断即可。
【详解】由分析可知,阴影部分是扇形的是。
故答案为:A
【点睛】解答本题关键是深刻理解扇形的意义。
6.B
【分析】根据圆的面积公式:π×半径2,求出大圆面积和小圆面积,再用小圆面积除以大圆面积,即可解答。
【详解】大圆面积:π×52=25π(平方厘米)
小圆面积:π×42=16π(平方厘米)
16π÷25π=
故答案为:B
【点睛】本题考查圆的面积公式的应用,以及求一个数是另一个数的几分之几。
7.B
【分析】观察图形可知,3个圆的圆心连接是一个等边三角形,根据等边三角形的特征,三个内角相等,都等于60°;阴影部分面积是3个圆心角为60°的扇形面积和;60°×3=180°,阴影部分面积就是半径为2cm圆的面积的一半,根据圆的面积公式:π×半径2,代入数据,求出一个圆的面积,再除以2,就是这个阴影部分的面积。21cnjy.com
【详解】3.14×22÷2
=3.14×4÷2
=12.56÷2
=6.28(cm2)
故答案选:B
【点睛】本题考查等边三角形的特征,圆的面积公式的应用,解答本题的关键是明确阴影部分面积等于半径为2cm圆的面积的一半。2-1-c-n-j-y
8.A
【分析】由于铁丝围成一个圆,再围成一个正方形, 则圆和正方形的周长相等,根据圆的周长公式:C=2πr,求出铁丝的长度,再根据正方形的周长公式:边长×4,把数代入即可求解。
【详解】3.14×2×8
=6.28×8
=50.24(厘米)
50.24÷4=12.56(厘米)
故答案为:A
【点睛】本题主要考查正方形和圆的周长公式,熟练掌握它们的公式并灵活运用。
9.3.14
【分析】先明确π=3.1415926…,然后按照小数比较大小的方法,先比较小数的整数部分,如果整数部分相同,再比较小数的十分位,如果十分位也相同,再比较小数的百分位……以此比较即可。
【详解】π=3.1415926…
3.14<3.141414…<π<3.142
所以在3.14,π,3.142,3.141414…这四个数中,最小的数是3.14。
【点睛】本题考查了小数比较大小的方法,按照小数比较大小的方法,先比较小数的整数部分,如果整数部分相同,再比较小数的十分位,如果十分位也相同,再比较小数的百分位……以此比较即可。
10.5
【分析】根据圆的周长公式分别求出大轮和小轮的周长,再用大轮的周长除以小轮的周长,求出大轮转1周,小轮要转多少周即可。
【详解】3.14×6÷(3.14×1.2)
=18.84÷3.768
=5(周)
【点睛】本题考查了圆周长的应用,灵活运用圆的周长公式是解题的关键。
11. 3∶2 9∶4
【分析】根据圆的周长公式:C=2πr,圆的面积公式:S=πr2,因为圆周率是一定,所以圆的周长与半径成正比例,也就是大小圆的周长的比等于大小圆半径的比,大小圆面积的比等于大小圆半径平方的比;据此解答即可。【来源:21cnj*y.co*m】
【详解】因为大小圆半径的比是3∶2,所以大小圆周长的比是3∶2
大小圆面积的比是32∶22=9∶4。
【点睛】此题主要考查圆的周长公式、面积公式的灵活运用,比的意义及应用,关键是熟记公式。
12.31.4
【分析】根据正方形面积公式:正方形面积=边长×边长;观察图形可知,正方形的边长等于圆的直径,正方形面积=4×半径×半径,半径×半径=40÷4=10;根据圆的面积=π×半径×半径,即圆的面积=π×(正方形面积÷4),代入数据,即可解答。【版权所有:21教育】
【详解】3.14×(40÷4)
=3.14×10
=31.4(平方厘米)
【点睛】解答此题的关键是理解正方形的边长等于圆的直径,半径的平方=正方形面积÷4。
13.7.85
【分析】正方形的面积是边长的平方,又知正方形面积是10平方厘米,即正方形边长2=10平方厘米,正方形的边长又是这个圆的半径,即r2=10平方厘米,根据圆的面积S=πr2,即可求出这个圆的面积,进而求出这个圆的面积。
【详解】3.14×10×
=31.4×
=7.85(平方厘米)
【点睛】本题是考查阴影部分的面积,解答此题的关键是明确正方形的面积就是这个圆的半径的平方。
14. 2 32
【分析】通过观察图形可知,这个图形有2条对称轴,根据圆的周长公式:C=πd,那么d=C÷π,据此求出圆的直径,长方形的长等于直径的2倍,长方形的宽等于直径,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】由图可知,这个图形有2条对称轴,
12.56÷3.14=4(cm)
4×2×4
=8×4
=32(cm2)
【点睛】此题考查的目的是理解掌握轴对称图形的特征及应用,圆的周长公式、长方形的面积公式及应用,关键是熟记公式。
15. 3 1
【分析】假设出正方形的边长,第1图中圆的半径是边长的,第3图中每个圆的半径是正方形边长的,根据“”“”求出圆的周长和面积,最后用除法计算出它们的倍数关系,据此解答。
【详解】假设正方形边长为1厘米,第1图中圆的半径为厘米,直径为×2=1厘米,第3图中圆的半径为厘米,直径为×2=厘米。
第1图圆的周长:×1=(厘米)
第3图圆的周长:××9=3(厘米)
3÷=3
所以,第3图中所有圆周长的和是第1图中圆周长的3倍。
第1图圆的面积:×()2=(平方厘米)
第3图圆的面积:×()2×9
=××9
=(平方厘米)
÷=1
所以,第3图所有圆的面积和是第1图中圆面积的1倍。
【点睛】掌握圆的周长和面积的计算公式是解答题目的关键。
16.100
【分析】观察图形可知,圆的直径相当于正方形边长,根据圆的周长公式:C=πd,据此求出正方形的边长,再根据正方形的面积=边长×边长,据此解答即可。
【详解】31.4÷3.14=10(厘米)
10×10=100(平方厘米)
【点睛】本题考查圆的周长,明确圆的直径相当于正方形的边长是解题的关键。
17.√
【分析】半径决定圆的大小,一个整圆的圆心角是360°,所以用4个半径相等且圆心角是90°的扇形可以拼成一个圆。据此判断即可。【来源:21·世纪·教育·网】
【详解】由分析可知:
因为4个扇形的半径相等,且圆心角都是90°,所以可以拼成一个圆。原题干说法正确。
故答案为:√
【点睛】本题考查扇形和圆心角,明确半径决定圆的大小是解题的关键。
18.√
【分析】根据题意,设圆的直径为d,增加1倍后的直径为2d,根据圆的面积公式可分别计算出直径增加前和增加后圆的面积,然后再用增加后的面积除以原来的面积即可。
【详解】设圆的直径为d,圆的半径为,增加1倍后的直径为2d,圆的半径为d
原来的面积为:π()2
增加后的面积为:πd2
所以πd2÷π()2=4
【点睛】本题考查了圆的面积知识,完成本题要在了解圆的面积公式的基础上进行。
19.×
【分析】半圆的周长应是圆周长的一半再加一条直径,据此判断即可。
【详解】半圆的周长不等于圆周长的一半,还需要再加上一条直径,原题说法错误;
故答案为:×。
【点睛】明确半圆周长的含义是解答本题的关键。
20.×
【分析】根据圆的面积公式S=,代入数据判断即可。
【详解】
=3.14×4
=12.56(平方厘米)
=3.14×1×2
=6.28(平方厘米)
12.56>6.28
故答案为:×
【点睛】本题考查了圆的面积的计算方法,应理解掌握,灵活运用。
21.×
【分析】依据轴对称图形的定义:一个圆形沿一条直径所在的直线对折,对折后的两部分都能完全重合,所以,任一条直径所在的直线都是它的对称轴。即可作答。
【详解】沿圆的每一条直径所在的直线对折,对折后的两部分都能完全重合,所以,任一条直径所在的直线都是它的对称轴,因此圆的直径不是其对称轴,圆的直径所在的直线是其对称轴。21*cnjy*com
故答案为:×
【点睛】解答此题的关键是明白对称轴是直线,而圆的直径是线段。
22.周长:35.7厘米;
面积:21.5平方厘米
【分析】观察图形可知,阴影部分的周长=半径为10厘米圆周长的+2个半径的长度;阴影部分的面积=边长为10厘米的正方形的面积-半径为10厘米圆面积的;据此即可解答问题。
【详解】周长:
3.14×10×2×+10×2
=15.7+20
=35.7(厘米)
面积:
10×10-10×10×3.14×
=100-78.5
=21.5(平方厘米)
23.251.2平方厘米
【分析】阴影部分是一个圆环,圆环的面积=π(R2-r2),据此解答。
【详解】3.14×(122-82)
=3.14×(144-64)
=3.14×80
=251.2(平方厘米)
24.388.575平方米
【分析】先利用塔蝶直径求出外圆的半径,减去环宽4.5米,就是内圆的半径,再利用圆环的面积公式:即可求出环形露天观光平台的面积。
【详解】32÷2=16(米)
16-4.5=11.5(米)
=
=
=(平方米)
答:环形露天观光平台的面积是388.575平方米。
【点睛】此题的解题关键是掌握圆环的面积的计算方法。
25.351.68平方米
【分析】一个圆形花坛,原来直径是24米,扩建后的直径与原来直径的比是4:3,则原来的直径是扩建后的,用除法即可求出扩建后的直径;根据圆的面积公式分别求出扩建前和扩建后花坛的面积,进而求出增加了多少。www.21-cn-jy.com
【详解】24÷=32(米)
3.14×(32÷2) -3.14×(24÷2)
=3.14×16 -3.14×12
=3.14×256-3.14×144
=803.84-452.16
=351.68(平方米)
答:扩建后花坛的面积增加了351.68平方米。
【点睛】解答此题的关键本是根据比与分数的关系,知道原来的直径是扩建后的直径几分之几,求出扩建后的直径,进而求出扩建后花坛的面积与原来相差多少。
26.0.9米
【分析】求绳子的长度减去剩余的的绳子长,除以10圈,得到一圈的长度,利用圆的周长,求出树干的直径。21·cn·jy·com
【详解】
(米)
答:这棵树干的直径大约是0.9米。
【点睛】此题的解题关键是利用圆的周长公式,求出正确的答案。
27.254.34平方分米
【分析】由题意可知:桌布的直径比圆桌的直径长3+3=6分米,由此得出桌布的直径,带入圆的面积公式即可求出桌布的面积。21·世纪*教育网
【详解】12+3+3=18(分米)
3.14×(18÷2)2
=3.14×81
=254.34(平方分米)
答:这块桌布的面积是254.34平方分米。
【点睛】本题主要考查圆的面积公式的实际应用,求出桌布的直径是解题的关键。
28.(1)75.36平方米;
(2)14盏
【分析】(1)依据圆的面积公式,先求出扩宽后大圆的面积;接下来用大圆面积减去小圆面积,即可求出圆环面积;21世纪教育网版权所有
(2)根据在封闭图形上的植树问题,栽树的棵数=间隔数,用新展区圆周外围周长除以3.14求得一共需要安装多少盏装饰灯。
【详解】(1)10÷2=5(米)
3.14×(5+2)2-3.14×52
=3.14×49-3.14×25
=3.14×(49-25)
=3.14×24
=75.36(平方米)
答:新展区的面积比原来增加了75.36平方米。
(2)3.14×(10+2+2)÷3.14
=3.14×14÷3.14
=14(盏)
答:需要14盏装饰灯。
【点睛】本题考查了圆环面积的计算以及在封闭图形上的植树问题,知识点是:“环形的面积=大圆的面积-小圆的面积”,“栽树的棵数=间隔数”。www-2-1-cnjy-com
29.28千米
【分析】由题意知:先求得轮胎的周长,再乘300圈,得一分钟卡车行驶的距离,再乘30,得半小时行驶的距离。据此解答。
【详解】3.14×100×300×30
=314×300×30
=94200×30
=2826000(厘米)
≈28千米
答:这辆小汽车半小时行驶约28千米。
【点睛】本题考查了圆周长公式的运用。求得轮能胎的周长是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
