人教版(2019)数学必修第二册6.2.2向量的减法运算 课件(共42张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册6.2.2向量的减法运算 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 10:36:12 | ||
图片预览





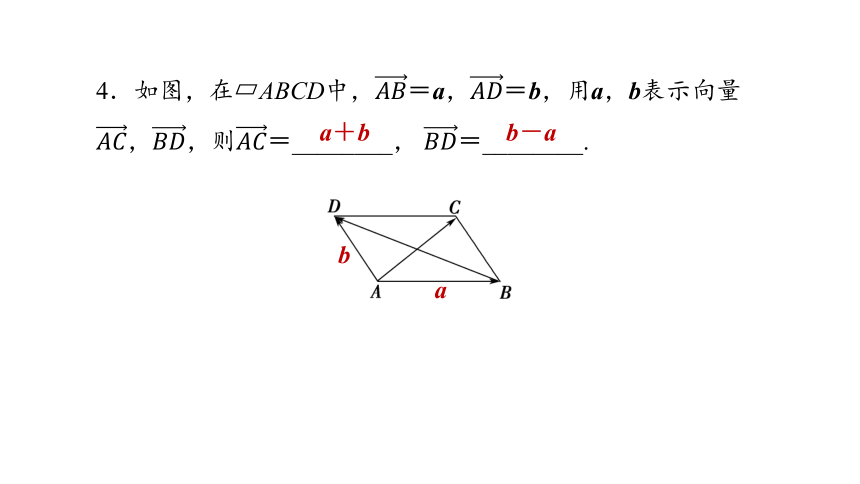





文档简介
(共42张PPT)
6.2.2 向量的减法运算
高一
必修二
本节目标
1.理解相反向量的含义,能用相反向量说出向量减法的意义.
2.掌握向量减法的运算及其几何意义,能熟练地进行向量的加减运算.
3.能将向量的减法运算转化为向量的加法运算.
课前预习
预习课本P11~12,思考并完成以下问题
(1) a的相反向量是什么?
(2)向量的减法运算及其几何意义是什么?
课前小测
1.非零向量m与n是相反向量,下列不正确的是( )
A.m=n B.m=-n
C.|m|=|n| D.方向相反
A
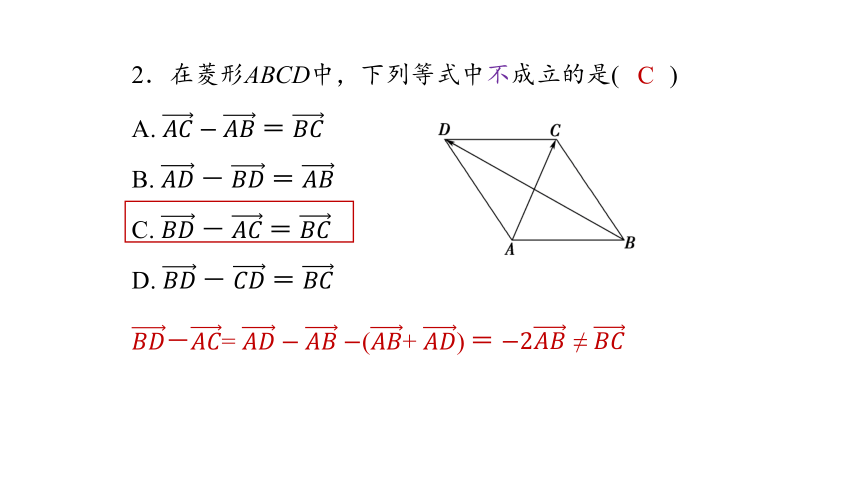
2.在菱形ABCD中,下列等式中不成立的是( )
A. =
B. - =
C. - =
D. - =
-= (+ )
=
≠
C
3.化简- + + 的结果等于( )
A. B.
C. D.
-++=()+(+)
=+0
=
B
4.如图,在 ABCD中,=a,=b,用a,b表示向量,,则=________, =________.
a
b
a+b
b-a
新知探究
1.相反向量
(1)定义:与向量a长度______,方向______的向量,
叫做a的相反向量.
(2)性质:①-(-a)=_____.
②对于相反向量有:a+(-a)=_____.
③若a,b互为相反向量,则a=______,a+b=____.
相等
相反
a
0
-b
0
2.向量的减法
(1)定义:a-b=a+(-b),即减去一个向量相当于
加上这个向量的__________.
(2)作法:在平面内任取一点O,作=a, =b,
则向量_____=a-b,如图所示.
相反向量
O
A
B
a
b
a-b
在什么条件下,|a-b|=|a|+|b|?
思考:
提示:当a,b至少有一者为0或a,b非零且反向时成立.
题型突破
典例深度剖析 重点多维探究
题型一 向量减法的几何意义
[例1] (1)如图所示,四边形ABCD中,若=a, =b, =c,则=( )
A.a-b+c B.b-(a+c)
C.a+b+c D.b-a+c
=
=
= a+c-b
A
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
则=a+b-c.
法一:几何意义法
在平面内任取一点O,作=a, =b,
O
A
a
B
b
则=a+b,
再作=c,
a+b
C
c
a+b-c
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
再作=-c,连接OC,则=a+b-c.
法二:定义法
在平面内任取一点O,
作=a, =b,则=a+b,
O
A
a
B
b
a+b
-c
C
a+b-c
方法总结
可以直接用向量减法的三角形法则,即把两向量的起点重合,则差向量为连接两个向量的终点,指向被减向量的终点的向量.
求作两个向量的差向量的两种思路
可以转化为向量的加法来进行,如a-b,可以先作-b,然后作a+(-b)即可.
跟踪训练
1.如图,已知向量a,b,c,求作向量a-b-c.
连接DB,得向量.则向量即为所求作的向量a-b-c.
法一:先作a-b,再作a-b-c即可.
以A为起点分别作向量和,使=a, =b.
连接CB,得向量=a-b,再以C为起点作向量,使=c,
A
B
a
C
b
a-b
D
c
a-b-c
跟踪训练
1.如图,已知向量a,b,c,求作向量a-b-c.
(2)作=a,则=a-b-c.
法二:先作-b,-c,再作a+(-b)+(-c).
A
B
-b
-c
C
a
O
a-b-c
(1)作=-b和=-c;
题型二 向量减法的运算及简单应用
②用b,c表示.
[例2] (1)如图所示,
①用a,b表示;
= - =--=-a-b.
=-=-(+ )=-b-c.
② (-)-(-);
(2)化简下列各向量的表达式:
① +-;
③ (++)-(--).
+-= -
=
(-)-(-) = (+)-(+)
=-
=
(+ +)-(--)
=-
=
= (+) -(-)
② (-)-(-);
一题多法
原式=--+
=(+)-(+)
= -
=0
法一:加法法则
法二:减法法则(利用相反向量)
原式=--+
=( -)+(-)
=+
=0
② (-)-(-);
一题多法
原式=--+
=(-)-(-)-(-) +(-)
=--+-++-
=0
法三:减法法则(创造同一起点)
方法总结
向量减法运算的常用方法
常用方法
可以通过相反向量,把向量减法的运算转化为加法运算
运用向量减法的三角形法则,此时要注意两个向量要有共同的起点
引入点O,逆用向量减法的三角形法则,将各向量起点统一
向量加减法化简的两种形式
(1)首尾相连且为和.
(2)起点相同且为差.
解题时要注意观察是否有这两种形式,同时注意逆向应用.
首先要利用向量加减的运算法则、运算律,
其次要分析图形的性质,通过图形中向量的相等、平行等关系辅助化简运算.
与图形相关的向量运算化简
跟踪训练
(1) - + - ;
2.化简下列向量表达式:
(2) (-)+(- ).
- + - = + -
= -
=
(-)+(- ) = + + +
= +( + +)
= +0
=
题型三 向量减法几何意义的应用
1.以向量加法的平行四边形法则为基础,能否构造一个图形将a+b和a-b放在这个图形中?
探究问题
提示:如图所示,平行四边形ABCD中,=a,=b,则a+b=,a-b= .
2.已知向量a,b,那么||a|-|b||与|a±b|及|a|+|b|三者具有什么样的大小关系?
探究问题
提示:它们之间的关系为||a|-|b|| ≤ |a±b| ≤ |a|+|b|.
O
A
a
B
b
a+b
(2)当a,b不共线时,作=a,=b,则a+b=,如图所示,根据三角形的性质,有||a|-|b|| <|a+b|<|a|+|b|.同理可证||a|-|b|| <|a-b|<|a|+|b|.
(1)当a,b有一个为零向量时,不等式显然成立.
2.已知向量a,b,那么||a|-|b||与|a±b|及|a|+|b|三者具有什么样的大小关系?
探究问题
(3)当a,b非零且共线时,
②当向量a,b反向时,不妨设|a|>|b|,作法同上,如图所示,此时|a+b|=|a|-|b|.
①当向量a与b同向时,作法同上,如图所示,此时|a+b|=|a|+|b|.
O
A
a
B
b
a+b
O
A
a
b
a+b
综上所述,得不等式||a|-|b||≤|a±b|≤|a|+|b|.
[例3] (1)在四边形ABCD中,=,若|-|=|-|,则四边形ABCD是( )
A.菱形 B.矩形
C.正方形 D.不确定
∵ = ,
∴四边形ABCD为平行四边形,
又∵| - |=|-|,
∴||=||.
∴四边形ABCD为矩形.
B
[例3] (2)已知||=6,||=9,求|-|的取值范围.
∵|||-|||≤|-|≤||+||,且||=9,||=6,
∴3≤|-|≤15.
当与同向时,| - |=3;
当与反向时,| - |=15.
∴| - |的取值范围为[3,15].
多维探究
变式1 将本例(2)的条件改为“||=8,||=5”,求||的取值范围.
因为= - ,||=8,||=5,
|||-|||≤|- |≤||+||,
所以3≤||≤13,
当与同向时,||=3;
当与反向时,||=13.
所以||的取值范围是[3,13].
变式2 在本例(2)条件不变的条件下,求:|+|的取值范围.
由|||-|||≤|+|≤||+||,
∵||=6,||=9,
∴3≤|+|≤15.
当与同向时,| + |=15;
当与反向时,| + |=3.
变式3 本例(2)中条件“||=9”改为“||=9”,求||的取值范围.
= - ,又||=||,
由|||-|||≤|-|≤||+||,
∴3≤||≤15.
反思感悟
(2)化归为向量问题,进行向量运算.
1.用向量法解决平面几何问题的步骤
(1)将平面几何问题中的量抽象成向量.
(3)将向量问题还原为平面几何问题.
反思感悟
(1)利用向量证明线段平行且相等,从而证明四边形为平行四边形,只需证明对应有向线段所表示的向量相等即可.
2.用向量法证明四边形为平行四边形的方法和解题关键
(2)根据图形灵活应用向量的运算法则,找到向量之间的关系是解决此类问题的关键.
随堂检测
1.判断正误
(1) 0-a=-a;( )
(2) -(-a)=a;( )
(3) a+(-a)=0;( )
(4) a+0=a;( )
(5) a-b=a+(-b);( )
(6) a+(-a)=0.( )
√
√
√
√
√
×
2.化简-+-=________.
-+-
= ( +)+(-)
= +
=
3.若a,b为相反向量,且|a|=1,|b|=1,则|a+b|=________,|a-b|=________.
因为a,b为相反向量,
∴a+b=0,即|a+b|=0,
又a=-b,
∴|a-b|=|2a|=2.
0
2
4.若a≠0,b≠0且|a|=|b|=|a-b|,求a与a+b所在直线的夹角.
所以△OAB是等边三角形,
所以∠BOA=60°.
a
b
如图,设=a, =b,
则a-b= = ,
因为|a|=|b|=|a-b|,
所以| |=| |=||,
因为=a+b,且在菱形OACB中,对角线OC平分∠BOA.
所以a与a+b所在直线的夹角为30°.
本课小结
3.以平行四边形ABCD的两邻边AB,AD分别表示向量=a,=b,则两条对角线表示的向量为=a+b,=b-a,=a-b,这一结论在以后应用非常广泛,应该加强理解并掌握.
1.向量减法的实质是向量加法的逆运算.利用相反向量的定义,-= 就可以把减法转化为加法.即减去一个向量等于加上这个向量的相反向量.如a-b=a+(-b).
2.在用三角形法则作向量减法时,要注意“差向量连接两向量的终点,箭头指向被减向量”.解题时要结合图形,准确判断,防止混淆.
通过本节课,你学会了什么?
6.2.2 向量的减法运算
高一
必修二
本节目标
1.理解相反向量的含义,能用相反向量说出向量减法的意义.
2.掌握向量减法的运算及其几何意义,能熟练地进行向量的加减运算.
3.能将向量的减法运算转化为向量的加法运算.
课前预习
预习课本P11~12,思考并完成以下问题
(1) a的相反向量是什么?
(2)向量的减法运算及其几何意义是什么?
课前小测
1.非零向量m与n是相反向量,下列不正确的是( )
A.m=n B.m=-n
C.|m|=|n| D.方向相反
A
2.在菱形ABCD中,下列等式中不成立的是( )
A. =
B. - =
C. - =
D. - =
-= (+ )
=
≠
C
3.化简- + + 的结果等于( )
A. B.
C. D.
-++=()+(+)
=+0
=
B
4.如图,在 ABCD中,=a,=b,用a,b表示向量,,则=________, =________.
a
b
a+b
b-a
新知探究
1.相反向量
(1)定义:与向量a长度______,方向______的向量,
叫做a的相反向量.
(2)性质:①-(-a)=_____.
②对于相反向量有:a+(-a)=_____.
③若a,b互为相反向量,则a=______,a+b=____.
相等
相反
a
0
-b
0
2.向量的减法
(1)定义:a-b=a+(-b),即减去一个向量相当于
加上这个向量的__________.
(2)作法:在平面内任取一点O,作=a, =b,
则向量_____=a-b,如图所示.
相反向量
O
A
B
a
b
a-b
在什么条件下,|a-b|=|a|+|b|?
思考:
提示:当a,b至少有一者为0或a,b非零且反向时成立.
题型突破
典例深度剖析 重点多维探究
题型一 向量减法的几何意义
[例1] (1)如图所示,四边形ABCD中,若=a, =b, =c,则=( )
A.a-b+c B.b-(a+c)
C.a+b+c D.b-a+c
=
=
= a+c-b
A
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
则=a+b-c.
法一:几何意义法
在平面内任取一点O,作=a, =b,
O
A
a
B
b
则=a+b,
再作=c,
a+b
C
c
a+b-c
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
再作=-c,连接OC,则=a+b-c.
法二:定义法
在平面内任取一点O,
作=a, =b,则=a+b,
O
A
a
B
b
a+b
-c
C
a+b-c
方法总结
可以直接用向量减法的三角形法则,即把两向量的起点重合,则差向量为连接两个向量的终点,指向被减向量的终点的向量.
求作两个向量的差向量的两种思路
可以转化为向量的加法来进行,如a-b,可以先作-b,然后作a+(-b)即可.
跟踪训练
1.如图,已知向量a,b,c,求作向量a-b-c.
连接DB,得向量.则向量即为所求作的向量a-b-c.
法一:先作a-b,再作a-b-c即可.
以A为起点分别作向量和,使=a, =b.
连接CB,得向量=a-b,再以C为起点作向量,使=c,
A
B
a
C
b
a-b
D
c
a-b-c
跟踪训练
1.如图,已知向量a,b,c,求作向量a-b-c.
(2)作=a,则=a-b-c.
法二:先作-b,-c,再作a+(-b)+(-c).
A
B
-b
-c
C
a
O
a-b-c
(1)作=-b和=-c;
题型二 向量减法的运算及简单应用
②用b,c表示.
[例2] (1)如图所示,
①用a,b表示;
= - =--=-a-b.
=-=-(+ )=-b-c.
② (-)-(-);
(2)化简下列各向量的表达式:
① +-;
③ (++)-(--).
+-= -
=
(-)-(-) = (+)-(+)
=-
=
(+ +)-(--)
=-
=
= (+) -(-)
② (-)-(-);
一题多法
原式=--+
=(+)-(+)
= -
=0
法一:加法法则
法二:减法法则(利用相反向量)
原式=--+
=( -)+(-)
=+
=0
② (-)-(-);
一题多法
原式=--+
=(-)-(-)-(-) +(-)
=--+-++-
=0
法三:减法法则(创造同一起点)
方法总结
向量减法运算的常用方法
常用方法
可以通过相反向量,把向量减法的运算转化为加法运算
运用向量减法的三角形法则,此时要注意两个向量要有共同的起点
引入点O,逆用向量减法的三角形法则,将各向量起点统一
向量加减法化简的两种形式
(1)首尾相连且为和.
(2)起点相同且为差.
解题时要注意观察是否有这两种形式,同时注意逆向应用.
首先要利用向量加减的运算法则、运算律,
其次要分析图形的性质,通过图形中向量的相等、平行等关系辅助化简运算.
与图形相关的向量运算化简
跟踪训练
(1) - + - ;
2.化简下列向量表达式:
(2) (-)+(- ).
- + - = + -
= -
=
(-)+(- ) = + + +
= +( + +)
= +0
=
题型三 向量减法几何意义的应用
1.以向量加法的平行四边形法则为基础,能否构造一个图形将a+b和a-b放在这个图形中?
探究问题
提示:如图所示,平行四边形ABCD中,=a,=b,则a+b=,a-b= .
2.已知向量a,b,那么||a|-|b||与|a±b|及|a|+|b|三者具有什么样的大小关系?
探究问题
提示:它们之间的关系为||a|-|b|| ≤ |a±b| ≤ |a|+|b|.
O
A
a
B
b
a+b
(2)当a,b不共线时,作=a,=b,则a+b=,如图所示,根据三角形的性质,有||a|-|b|| <|a+b|<|a|+|b|.同理可证||a|-|b|| <|a-b|<|a|+|b|.
(1)当a,b有一个为零向量时,不等式显然成立.
2.已知向量a,b,那么||a|-|b||与|a±b|及|a|+|b|三者具有什么样的大小关系?
探究问题
(3)当a,b非零且共线时,
②当向量a,b反向时,不妨设|a|>|b|,作法同上,如图所示,此时|a+b|=|a|-|b|.
①当向量a与b同向时,作法同上,如图所示,此时|a+b|=|a|+|b|.
O
A
a
B
b
a+b
O
A
a
b
a+b
综上所述,得不等式||a|-|b||≤|a±b|≤|a|+|b|.
[例3] (1)在四边形ABCD中,=,若|-|=|-|,则四边形ABCD是( )
A.菱形 B.矩形
C.正方形 D.不确定
∵ = ,
∴四边形ABCD为平行四边形,
又∵| - |=|-|,
∴||=||.
∴四边形ABCD为矩形.
B
[例3] (2)已知||=6,||=9,求|-|的取值范围.
∵|||-|||≤|-|≤||+||,且||=9,||=6,
∴3≤|-|≤15.
当与同向时,| - |=3;
当与反向时,| - |=15.
∴| - |的取值范围为[3,15].
多维探究
变式1 将本例(2)的条件改为“||=8,||=5”,求||的取值范围.
因为= - ,||=8,||=5,
|||-|||≤|- |≤||+||,
所以3≤||≤13,
当与同向时,||=3;
当与反向时,||=13.
所以||的取值范围是[3,13].
变式2 在本例(2)条件不变的条件下,求:|+|的取值范围.
由|||-|||≤|+|≤||+||,
∵||=6,||=9,
∴3≤|+|≤15.
当与同向时,| + |=15;
当与反向时,| + |=3.
变式3 本例(2)中条件“||=9”改为“||=9”,求||的取值范围.
= - ,又||=||,
由|||-|||≤|-|≤||+||,
∴3≤||≤15.
反思感悟
(2)化归为向量问题,进行向量运算.
1.用向量法解决平面几何问题的步骤
(1)将平面几何问题中的量抽象成向量.
(3)将向量问题还原为平面几何问题.
反思感悟
(1)利用向量证明线段平行且相等,从而证明四边形为平行四边形,只需证明对应有向线段所表示的向量相等即可.
2.用向量法证明四边形为平行四边形的方法和解题关键
(2)根据图形灵活应用向量的运算法则,找到向量之间的关系是解决此类问题的关键.
随堂检测
1.判断正误
(1) 0-a=-a;( )
(2) -(-a)=a;( )
(3) a+(-a)=0;( )
(4) a+0=a;( )
(5) a-b=a+(-b);( )
(6) a+(-a)=0.( )
√
√
√
√
√
×
2.化简-+-=________.
-+-
= ( +)+(-)
= +
=
3.若a,b为相反向量,且|a|=1,|b|=1,则|a+b|=________,|a-b|=________.
因为a,b为相反向量,
∴a+b=0,即|a+b|=0,
又a=-b,
∴|a-b|=|2a|=2.
0
2
4.若a≠0,b≠0且|a|=|b|=|a-b|,求a与a+b所在直线的夹角.
所以△OAB是等边三角形,
所以∠BOA=60°.
a
b
如图,设=a, =b,
则a-b= = ,
因为|a|=|b|=|a-b|,
所以| |=| |=||,
因为=a+b,且在菱形OACB中,对角线OC平分∠BOA.
所以a与a+b所在直线的夹角为30°.
本课小结
3.以平行四边形ABCD的两邻边AB,AD分别表示向量=a,=b,则两条对角线表示的向量为=a+b,=b-a,=a-b,这一结论在以后应用非常广泛,应该加强理解并掌握.
1.向量减法的实质是向量加法的逆运算.利用相反向量的定义,-= 就可以把减法转化为加法.即减去一个向量等于加上这个向量的相反向量.如a-b=a+(-b).
2.在用三角形法则作向量减法时,要注意“差向量连接两向量的终点,箭头指向被减向量”.解题时要结合图形,准确判断,防止混淆.
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
