人教版(2019)数学必修第二册6.3.2~6.3.3平面向量的正交分解及坐标表示和加、减运算的坐标表示课件(共36张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册6.3.2~6.3.3平面向量的正交分解及坐标表示和加、减运算的坐标表示课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 10:47:29 | ||
图片预览










文档简介
(共36张PPT)
6.3.2~6.3.3 平面向量的正交分解及坐标表示和加、减运算的坐标表示
高一
必修二
情境引入
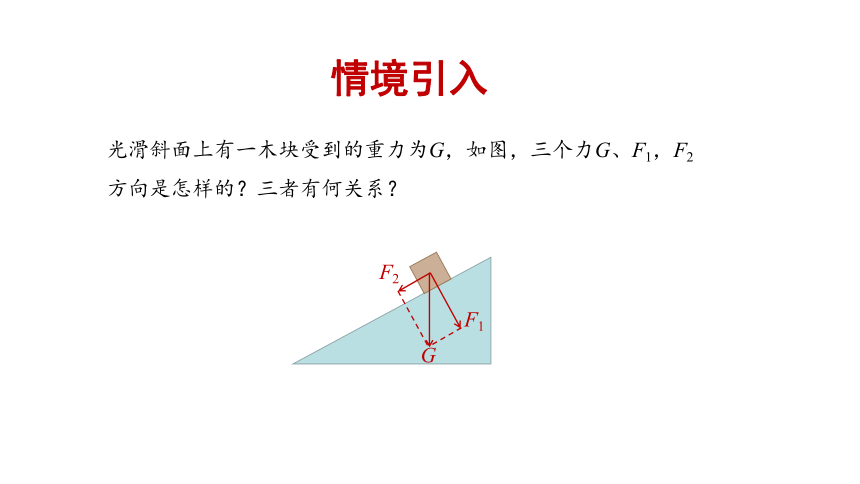
光滑斜面上有一木块受到的重力为G,如图,三个力G、F1,F2方向是怎样的?三者有何关系?
F1
F2
G
本节目标
1.了解平面向量的正交分解,掌握向量的坐标表示.
2.理解向量坐标的概念,掌握两个向量和、差的坐标运算法则.
3.向量的坐标与平面内点的坐标的区别与联系.
课前预习
预习课本P27~30,思考并完成以下问题
(1)怎样分解一个向量才为正交分解?
(2)如何由a,b的坐标求a+b,a-b的坐标?
课前小测
1.已知a=(3, 5),b=(-3, 2),则a+b=( )
A.(8, -1) B.(0, 7)
C.(7, 0) D.(-1, 8)
a+b=(3, 5)+(-3, 2)=(3-3, 5+2)=(0, 7)
B
2.已知向量a=(1, 2),b=(3, 1),则a-b等于( )
A.(-2, 1) B.(2, -1)
C.(2, 0) D.(4, 3)
a-b=(1, 2)-(3, 1)
=(1-3, 2-1)
=(-2, 1)
A
3.已知点A(1,-2),点B(4, 0),则向量=________.
= (4, 0)-(1,-2)
= (4-1, 0+2)
= (3, 2)
(3, 2)
4.如图,在平面直角坐标系中,分别取与x轴,y轴方向相同的两个单位向量i,j,以{i,j}作为基底,对于平面内的一个向量a,若|a|=2,θ=45°,则向量a的坐标为________.
a=2cos 45°i+2sin 45°j
= i+ j
=(, ).
(, )
新知探究
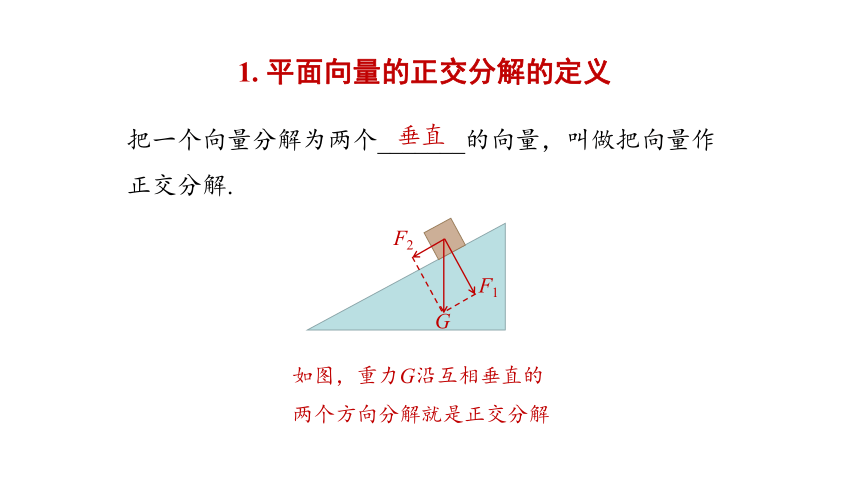
1. 平面向量的正交分解的定义
把一个向量分解为两个_______的向量,叫做把向量作正交分解.
垂直
F1
F2
G
如图,重力G沿互相垂直的两个方向分解就是正交分解
2.平面向量的坐标表示
在平面直角坐标系中,设与x轴、y轴方向相同的两个__________分别为i,j,取{i,j}作为基底. 对于平面内的任意一个向量a,由平面向量基本定理可知,有且只有一对实数x,y,使得a=_______.我们把有序数对(x,y)叫做向量a的坐标,记作_________. 此式叫做向量a的坐标表示.
定义
单位向量
xi+yj
a=(x,y)
x
y
O
i
j
a
特殊向量的坐标
i=(1,0),
j=(0,1),
0=(0,0).
x
y
O
i
j
a
a
A(x,y)
x
y
向量的坐标与点的坐标
知识点睛
以原点O为起点,作=a,
则点A的位置由向量a唯一确定.
设=xi+yi,则向量的坐标(x,y)就是终点A的坐标;
反过来,终点A的坐标(x,y)就是向量的坐标.
设向量a=(x1,y1),b=(x2,y2),λ∈R,则有下表:
3.平面向量的坐标运算
文字描述 符号表示
加法 两个向量和的坐标分别等于这两个向量相应坐标的_____ a+b=___________________
减法 两个向量差的坐标分别等于这两个向量相应坐标的_____ a-b=___________________
数乘 实数与向量的积的坐标等于用这个实数乘原来向量的___________ λa=____________
向量 坐标 公式 一个向量的坐标等于表示此向量的有向线段的_____的坐标减去_____的坐标 已知A(x1,y1),B(x2,y2),则=________________
和
差
(x1+x2,y1+y2)
(x1-x2,y1-y2)
相应坐标
(λx1,λy1)
终点
起点
(x2-x1,y2-y1)
题型突破
典例深度剖析 重点多维探究
题型一 平面向量的坐标表示
[例1] 如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,=a,=b.四边形OABC为平行四边形.
(1)求向量a,b的坐标;
(2)求向量的坐标;
(3)求点B的坐标.
[例1] 如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,=a,=b.四边形OABC为平行四边形.
(1)求向量a,b的坐标;
∴A(2,2),故a=(2,2).
∵∠AOC=180°-105°=75°,∠AOy=45°,
∴∠COy=30°.又OC=AB=3,
作AM⊥x轴于点M,
则OM=OA·cos 45°=4×=2,
AM=OA·sin 45°=4×=2,
∴C(, ),∴ = =(, ) ,
即b= (, ).
[例1] 如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,=a,=b.四边形OABC为平行四边形.
(2)求向量的坐标;
=(,)
[例1] 如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,=a,=b.四边形OABC为平行四边形.
(3)求点B的坐标.
=
=(2,2)
=(2,2)
所以点B的坐标(2,2).
方法总结
求向量坐标的三个步骤
平移
求角
求坐标
将向量的始点移至坐标原点
找出以x轴正向为始边,向量所在射线为终边的角
根据x=rcos, y=rcos(r为向量的模)求终点坐标,即为向量坐标
跟踪训练
1.已知向量a在射线y=x(x≥0)上,且起点为坐标原点O,又|a|= ,分别取与x轴、y轴方向相同的两个单位向量i,j作为基底,则向量a的坐标为( )
A.(1, 1) B.(-1, -1)
C.(, ) D.(-, -)
a=(cos 45°)i+(sin 45°)j=i+j=(1, 1).
A
题型二 平面向量的坐标运算
[例2] (1)已知点A(0,1),B(3,2),向量=(-4, -3),则向量=( )
A.(-7,-4) B.(7, 4)
C.(-1, 4) D.(1, 4)
从而=(-4, -2)-(3, 2)=(-7, -4).
法一
设C(x,y),
则=(x, y-1)=(-4, -3),
所以 ,
A
题型二 平面向量的坐标运算
[例2] (1)已知点A(0,1),B(3,2),向量=(-4, -3),则向量=( )
A.(-7,-4) B.(7, 4)
C.(-1, 4) D.(1, 4)
法二
A
= -=(-4, -3)-(3, 1)=(-7, -4).
=(3, 2)-(0, 1)=(3, 1),
题型二 平面向量的坐标运算
[例2] (2)已知向量a,b的坐标分别是(-1, 2),(3, -5),求a+b,a-b的坐标.
a - b=(-1, 2)-(3, -5)
a + b =(-1, 2)+(3, -5)
=(-1+3, 2-5)
=(2, -3)
=(-1-3, 2+5)
=(-4, 7)
方法总结
(1)若已知向量的坐标,则直接应用两个向量和、差的运算法则进行.
(2)若已知有向线段两端点的坐标,则必须先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可类比数的运算进行.
平面向量坐标(线性)运算的方法
跟踪训练
2.若A,B,C三点的坐标分别为(2,-4),(0, 6),(-8, 10),求+, -的坐标.
∴ + =(-2,10)+(-8,4)=(-10,14),
-=(-8, 4)-(-10, 14)=(2, -10).
∵ =(-2, 10), =(-8, 4), =(-10, 14),
题型三 平面向量坐标运算的应用
[例3] 已知四边形ABCD的三个顶点A(0, 2),B(-1,-2),C(3, 1),且= ,则顶点D的坐标为( )
A. B.
C.(4, 5) D.(1, 3)
设点D(m,n),
=
(4, 3)=(m,n-2)
D(4,5)
C
方法总结
在平面几何问题中解决向量问题,可以借助平行四边形对边平行且相等,也可利用平行四边形法则求解.
跟踪训练
3.如果将=绕原点O逆时针方向旋转120°得到,则的坐标是( )
A. B.
C.(-1, ) D.
D
因为=所在直线的倾斜角为30°,绕原点O逆时针方向旋转120°得到所在直线的倾斜角为150°,所以A,B两点关于y轴对称,由此可知B点坐标为,故的坐标是.
随堂检测
1.判断正误
(1)相等向量的坐标相同.( )
(2)平面上一个向量对应于平面上唯一的坐标.( )
(3)一个坐标对应于唯一的一个向量.( )
(4)平面上一个点与以原点为始点,该点为终点的向量一一对应.( )
√
√
×
√
2.设i,j是平面直角坐标系内分别与x轴,y轴正方向相同的两个单位向量,O为坐标原点,若=4i+2j, =3i+4j,则+的坐标是( )
A.(1,-2) B.(7,6)
C.(5,0) D.(11,8)
+ =(4, 2)+(3, 4)=(7, 6)
B
=4i+2j
=(4, 2)
=3i+4j
=(3,4)
3.已知点A(-1,-2),B(4, 3),则的坐标为( )
A.(3, 1) B.(-5, -5)
C.(5, 5) D.(-5, 5)
=(4, 3)-(-1,-2)=(5, 5)
C
4.已知A(2,-3), =(3,-2),则点B的坐标为( )
A.(-5, 5) B.(5, -5)
C.(-1, 1) D.(1, 1)
=+=(2,-3)+(3,-2)=(5,-5).
B
A(2,-3)
= (2,-3)
=(3,-2)
B(5,-5)
5.已知点O是△ABC内一点,∠AOB=150°,∠BOC=90°,设=a, =b, =c且|a|=2,|b|=1,|c|=3,求向量,的坐标.(以O为坐标原点, 所在直线为x轴建立平面直角坐标系)
建立如图所示的平面直角坐标系.
因为||=1,∠AOB=150°,
所以B(-cos30°,sin30°),所以B(-,).
因为||=3,∠BOC=90°,
所以C(-3sin30°,-3cos30°),即C(-,-).
所以=(-,-)-(-,)=(,- ),
易知A(2,0),所以=(-, )-(2,0)=(- -2, ).
本课小结
1.在平面直角坐标系中,平面内的点、以原点为起点的向量、有序实数对三者之间建立一一对应关系.如图所示.
2.向量的坐标和其终点的坐标不一定相同.当且仅当向量的起点在原点时,向量的坐标才和其终点的坐标相同.
3.在进行向量坐标形式的运算时,要牢记公式,细心计算,防止符号错误.
通过本节课,你学会了什么?
6.3.2~6.3.3 平面向量的正交分解及坐标表示和加、减运算的坐标表示
高一
必修二
情境引入
光滑斜面上有一木块受到的重力为G,如图,三个力G、F1,F2方向是怎样的?三者有何关系?
F1
F2
G
本节目标
1.了解平面向量的正交分解,掌握向量的坐标表示.
2.理解向量坐标的概念,掌握两个向量和、差的坐标运算法则.
3.向量的坐标与平面内点的坐标的区别与联系.
课前预习
预习课本P27~30,思考并完成以下问题
(1)怎样分解一个向量才为正交分解?
(2)如何由a,b的坐标求a+b,a-b的坐标?
课前小测
1.已知a=(3, 5),b=(-3, 2),则a+b=( )
A.(8, -1) B.(0, 7)
C.(7, 0) D.(-1, 8)
a+b=(3, 5)+(-3, 2)=(3-3, 5+2)=(0, 7)
B
2.已知向量a=(1, 2),b=(3, 1),则a-b等于( )
A.(-2, 1) B.(2, -1)
C.(2, 0) D.(4, 3)
a-b=(1, 2)-(3, 1)
=(1-3, 2-1)
=(-2, 1)
A
3.已知点A(1,-2),点B(4, 0),则向量=________.
= (4, 0)-(1,-2)
= (4-1, 0+2)
= (3, 2)
(3, 2)
4.如图,在平面直角坐标系中,分别取与x轴,y轴方向相同的两个单位向量i,j,以{i,j}作为基底,对于平面内的一个向量a,若|a|=2,θ=45°,则向量a的坐标为________.
a=2cos 45°i+2sin 45°j
= i+ j
=(, ).
(, )
新知探究
1. 平面向量的正交分解的定义
把一个向量分解为两个_______的向量,叫做把向量作正交分解.
垂直
F1
F2
G
如图,重力G沿互相垂直的两个方向分解就是正交分解
2.平面向量的坐标表示
在平面直角坐标系中,设与x轴、y轴方向相同的两个__________分别为i,j,取{i,j}作为基底. 对于平面内的任意一个向量a,由平面向量基本定理可知,有且只有一对实数x,y,使得a=_______.我们把有序数对(x,y)叫做向量a的坐标,记作_________. 此式叫做向量a的坐标表示.
定义
单位向量
xi+yj
a=(x,y)
x
y
O
i
j
a
特殊向量的坐标
i=(1,0),
j=(0,1),
0=(0,0).
x
y
O
i
j
a
a
A(x,y)
x
y
向量的坐标与点的坐标
知识点睛
以原点O为起点,作=a,
则点A的位置由向量a唯一确定.
设=xi+yi,则向量的坐标(x,y)就是终点A的坐标;
反过来,终点A的坐标(x,y)就是向量的坐标.
设向量a=(x1,y1),b=(x2,y2),λ∈R,则有下表:
3.平面向量的坐标运算
文字描述 符号表示
加法 两个向量和的坐标分别等于这两个向量相应坐标的_____ a+b=___________________
减法 两个向量差的坐标分别等于这两个向量相应坐标的_____ a-b=___________________
数乘 实数与向量的积的坐标等于用这个实数乘原来向量的___________ λa=____________
向量 坐标 公式 一个向量的坐标等于表示此向量的有向线段的_____的坐标减去_____的坐标 已知A(x1,y1),B(x2,y2),则=________________
和
差
(x1+x2,y1+y2)
(x1-x2,y1-y2)
相应坐标
(λx1,λy1)
终点
起点
(x2-x1,y2-y1)
题型突破
典例深度剖析 重点多维探究
题型一 平面向量的坐标表示
[例1] 如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,=a,=b.四边形OABC为平行四边形.
(1)求向量a,b的坐标;
(2)求向量的坐标;
(3)求点B的坐标.
[例1] 如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,=a,=b.四边形OABC为平行四边形.
(1)求向量a,b的坐标;
∴A(2,2),故a=(2,2).
∵∠AOC=180°-105°=75°,∠AOy=45°,
∴∠COy=30°.又OC=AB=3,
作AM⊥x轴于点M,
则OM=OA·cos 45°=4×=2,
AM=OA·sin 45°=4×=2,
∴C(, ),∴ = =(, ) ,
即b= (, ).
[例1] 如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,=a,=b.四边形OABC为平行四边形.
(2)求向量的坐标;
=(,)
[例1] 如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,=a,=b.四边形OABC为平行四边形.
(3)求点B的坐标.
=
=(2,2)
=(2,2)
所以点B的坐标(2,2).
方法总结
求向量坐标的三个步骤
平移
求角
求坐标
将向量的始点移至坐标原点
找出以x轴正向为始边,向量所在射线为终边的角
根据x=rcos, y=rcos(r为向量的模)求终点坐标,即为向量坐标
跟踪训练
1.已知向量a在射线y=x(x≥0)上,且起点为坐标原点O,又|a|= ,分别取与x轴、y轴方向相同的两个单位向量i,j作为基底,则向量a的坐标为( )
A.(1, 1) B.(-1, -1)
C.(, ) D.(-, -)
a=(cos 45°)i+(sin 45°)j=i+j=(1, 1).
A
题型二 平面向量的坐标运算
[例2] (1)已知点A(0,1),B(3,2),向量=(-4, -3),则向量=( )
A.(-7,-4) B.(7, 4)
C.(-1, 4) D.(1, 4)
从而=(-4, -2)-(3, 2)=(-7, -4).
法一
设C(x,y),
则=(x, y-1)=(-4, -3),
所以 ,
A
题型二 平面向量的坐标运算
[例2] (1)已知点A(0,1),B(3,2),向量=(-4, -3),则向量=( )
A.(-7,-4) B.(7, 4)
C.(-1, 4) D.(1, 4)
法二
A
= -=(-4, -3)-(3, 1)=(-7, -4).
=(3, 2)-(0, 1)=(3, 1),
题型二 平面向量的坐标运算
[例2] (2)已知向量a,b的坐标分别是(-1, 2),(3, -5),求a+b,a-b的坐标.
a - b=(-1, 2)-(3, -5)
a + b =(-1, 2)+(3, -5)
=(-1+3, 2-5)
=(2, -3)
=(-1-3, 2+5)
=(-4, 7)
方法总结
(1)若已知向量的坐标,则直接应用两个向量和、差的运算法则进行.
(2)若已知有向线段两端点的坐标,则必须先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可类比数的运算进行.
平面向量坐标(线性)运算的方法
跟踪训练
2.若A,B,C三点的坐标分别为(2,-4),(0, 6),(-8, 10),求+, -的坐标.
∴ + =(-2,10)+(-8,4)=(-10,14),
-=(-8, 4)-(-10, 14)=(2, -10).
∵ =(-2, 10), =(-8, 4), =(-10, 14),
题型三 平面向量坐标运算的应用
[例3] 已知四边形ABCD的三个顶点A(0, 2),B(-1,-2),C(3, 1),且= ,则顶点D的坐标为( )
A. B.
C.(4, 5) D.(1, 3)
设点D(m,n),
=
(4, 3)=(m,n-2)
D(4,5)
C
方法总结
在平面几何问题中解决向量问题,可以借助平行四边形对边平行且相等,也可利用平行四边形法则求解.
跟踪训练
3.如果将=绕原点O逆时针方向旋转120°得到,则的坐标是( )
A. B.
C.(-1, ) D.
D
因为=所在直线的倾斜角为30°,绕原点O逆时针方向旋转120°得到所在直线的倾斜角为150°,所以A,B两点关于y轴对称,由此可知B点坐标为,故的坐标是.
随堂检测
1.判断正误
(1)相等向量的坐标相同.( )
(2)平面上一个向量对应于平面上唯一的坐标.( )
(3)一个坐标对应于唯一的一个向量.( )
(4)平面上一个点与以原点为始点,该点为终点的向量一一对应.( )
√
√
×
√
2.设i,j是平面直角坐标系内分别与x轴,y轴正方向相同的两个单位向量,O为坐标原点,若=4i+2j, =3i+4j,则+的坐标是( )
A.(1,-2) B.(7,6)
C.(5,0) D.(11,8)
+ =(4, 2)+(3, 4)=(7, 6)
B
=4i+2j
=(4, 2)
=3i+4j
=(3,4)
3.已知点A(-1,-2),B(4, 3),则的坐标为( )
A.(3, 1) B.(-5, -5)
C.(5, 5) D.(-5, 5)
=(4, 3)-(-1,-2)=(5, 5)
C
4.已知A(2,-3), =(3,-2),则点B的坐标为( )
A.(-5, 5) B.(5, -5)
C.(-1, 1) D.(1, 1)
=+=(2,-3)+(3,-2)=(5,-5).
B
A(2,-3)
= (2,-3)
=(3,-2)
B(5,-5)
5.已知点O是△ABC内一点,∠AOB=150°,∠BOC=90°,设=a, =b, =c且|a|=2,|b|=1,|c|=3,求向量,的坐标.(以O为坐标原点, 所在直线为x轴建立平面直角坐标系)
建立如图所示的平面直角坐标系.
因为||=1,∠AOB=150°,
所以B(-cos30°,sin30°),所以B(-,).
因为||=3,∠BOC=90°,
所以C(-3sin30°,-3cos30°),即C(-,-).
所以=(-,-)-(-,)=(,- ),
易知A(2,0),所以=(-, )-(2,0)=(- -2, ).
本课小结
1.在平面直角坐标系中,平面内的点、以原点为起点的向量、有序实数对三者之间建立一一对应关系.如图所示.
2.向量的坐标和其终点的坐标不一定相同.当且仅当向量的起点在原点时,向量的坐标才和其终点的坐标相同.
3.在进行向量坐标形式的运算时,要牢记公式,细心计算,防止符号错误.
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
