人教版(2019)数学必修第二册6.3.4平面向量数乘运算的坐标表示课件(共44张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册6.3.4平面向量数乘运算的坐标表示课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 00:00:00 | ||
图片预览





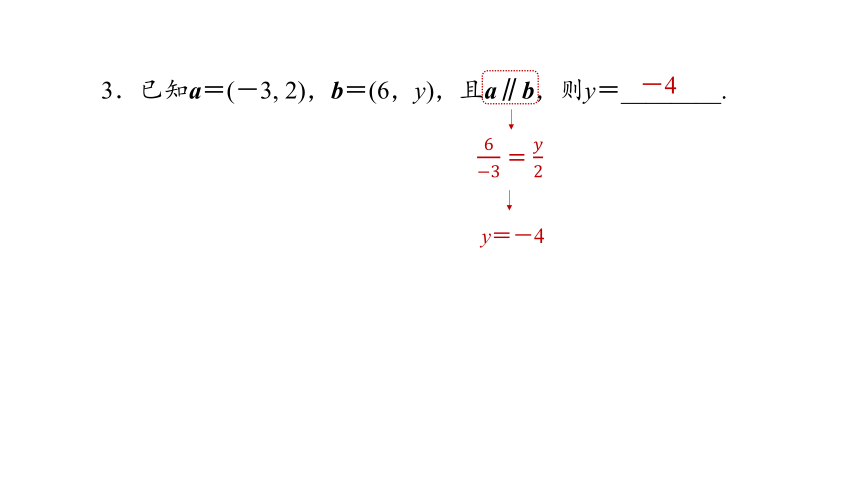






文档简介
(共44张PPT)
6.3.4 平面向量数乘运算的坐标表示
高一
必修二
本节目标
1.掌握向量数乘的坐标运算法则.
2.理解用坐标表示两向量共线的条件.
3.能根据平面向量的坐标,判断向量是否共线,并掌握三点共线的判断方法.
课前预习
预习课本P31~33,思考并完成以下问题
如何由a的坐标求λa的坐标?
(2) 如何利用向量的坐标运算表示两个向量共线?
课前小测
1.已知向量=(2, 4), =(0,2),则=( )
A.(-2, -2) B.(2, 2)
C.(1, 1) D.(-1, -1)
=
=
=
=
D
2.下列各对向量中,共线的是( )
A.a=(2, 3),b=(3, -2)
B.a=(2, 3),b=(4, -6)
C.a=(, -1),b=(1, )
D.a=(1, ),b=(, 2)
不共线
不共线
不共线
共线
b=a
D
3.已知a=(-3, 2),b=(6,y),且a∥b,则y=________.
y=-4
-4
4.若A(3, -6),B(-5, 2),C(6, y)三点共线,则y=_______.
∴-8(y+6)-8×3=0,解得y=-9.
=(-8, 8), =(3,y+6),
∵A,B,C三点共线,即∥ ,
-9
新知探究
已知a=(x,y),则λa=λ(x,y)=__________.
1.数乘运算的坐标表示
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
(1)符号表示
(λx,λy)
(2)文字描述
(2)如果用坐标表示,向量a,b(b≠0)共线的充要条件是______________.
2.平面向量共线的坐标表示
(1)设a=(x1,y1),b=(x2,y2),其中b≠0,a,b共线的充要条件是存在实数λ,使a=λb.
x1y2-x2y1=0
两向量a=(x1,y1),b=(x2,y2)共线的坐标条件能表示成吗?
思考
提示: 不一定,x2,y2有一者为零时,比例式没有意义,只有x2y2≠0时,才能使用.
题型突破
典例深度剖析 重点多维探究
题型一 向量共线的判定与证明
[例1] (1)下列各组向量中,共线的是( )
A.a=(-2, 3),b=(4, 6)
B.a=(2, 3),b=(3, 2)
C.a=(1, -2),b=(7, 14)
D.a=(-3, 2),b=(6, -4)
利用“纵横交错积相减”判断.
-2×6-3×4 ≠ 0
3×3-2×2 ≠ 0
1×14-(-2)×7≠0
(-3)×(-4)-2×6=0
D
(2)已知A(-1,-1),B(1,3),C(1,5),D(2,7),向量与平行吗?直线AB平行于直线CD吗?
∵ =(1-(-1),3-(-1))=(2,4),=(2-1,7-5)=(1,2).
又2×2-4×1=0,
∴ ∥ .
又=(2,6), =(2,4),
∴2×4-2×6≠0,
∴A,B,C不共线,
∴AB与CD不重合,
∴AB∥CD.
方法总结
向量共线的判定方法
提醒:向量共线的坐标表达式极易写错,如写成x1y1-x2y2=0或x1x2-y1y2=0都是不对的,因此要理解并记熟这一公式,可简记为:纵横交错积相减.
跟踪训练
1.已知A(1,-3),B (8, ) ,C(9,1),求证:A,B,C三点共线.
=(8-1, +3)= (7, ) , =(9-1,1+3)=(8,4),
∵7×4- ×8=0,
∴ ∥,且,有公共点A,
∴A,B,C三点共线.
题型二 已知平面向量共线求参数
[例2] 已知a=(1, 2),b=(-3, 2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?
法一:可利用b与非零向量a共线等价于b=λa(λ>0,b与a同向;λ<0,b与a反向)求解;
法二:可先利用坐标形式的等价条件求k,再利用b=λa判定同向还是反向.
!
思路探究
[例2] 已知a=(1, 2),b=(-3, 2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?
ka+b=k(1, 2)+(-3, 2)=(k-3, 2k+2),
a-3b=(1, 2)-3(-3, 2)=(10, -4),
当ka+b与a-3b平行时,存在唯一实数λ,使ka+b=λ(a-3b).
由(k-3, 2k+2)=λ(10, -4),
法一:(共线向量定理法)
所以
当k=-时,ka+b与a-3b平行,这时ka+b=-a+b=-(a-3b),
因为λ=-<0,所以ka+b与a-3b反向.
解得k=λ=-.
[例2] 已知a=(1, 2),b=(-3, 2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?
由题知ka+b=(k-3, 2k+2),a-3b=(10,-4),
因为ka+b与a-3b平行,
所以(k-3)×(-4)-10×(2k+2)=0,
解得k=-.
这时ka+b= (--3, -+2) =- (a-3b),
所以当k=-时,ka+b与a-3b平行,并且反向.
法二:(坐标法)
反思感悟
(1)利用共线向量定理a=λb(b≠0)列方程组求解.
(2)利用向量平行的坐标表达式x1y2-x2y1=0直接求解.
利用向量平行的条件处理求值问题的思路
跟踪训练
2.已知向量a=(1, 2),b=(2, -2),c=(1, λ),若c∥(2a+b),则λ=________.
λ=
2a+b=(4, 2)
c∥(2a+b),c=(1,λ)
4λ-2=0
题型三 向量共线的综合应用
[例3] (1)已知向量a=(cosα, -2),b=(sinα, 1),且a∥b,则2sinαcosα等于( )
A.3 B.-3
C.- D.
所以2sinαcosα= = ==-.
因为a∥b,所以cos α×1-(-2)×sin α=0,
即cosα=-2sin α,tanα=- ,
C
(2)如图所示,已知点A(4,0),B(4,4),C(2,6),求AC与OB的交点P的坐标.
由O,P,B三点共线,可设=λ=(4λ,4λ),
则=-=(4λ-4, 4λ),
= -=(-2, 6).
由与共线得(4λ-4)×6-4λ×(-2)=0,解得λ=,所以= =(3,3),所以P点的坐标为(3,3).
法一:(定理法)
(2)如图所示,已知点A(4,0),B(4,4),C(2,6),求AC与OB的交点P的坐标.
设P(x,y),则=(x,y),因为=(4,4),且与共线,所以,即x=y.
又=(x-4,y), =(-2,6),
且与共线,则(x-4)×6-y×(-2)=0,解得x=y=3,所以P点的坐标为(3,3).
法二:(坐标法)
方法总结
应用向量共线的坐标表示求解几何问题的步骤
跟踪训练
3.如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),=, =,AD与BC相交于点M,求点M的坐标.
因为= = (0,5)=(0, ),所以C (0, ).
因为= = (4,3)= (2, ) ,所以D (2, ).
设M(x,y),则=(x,y-5),
= (2-0, 5)= (2, ).
因为∥ ,所以-x-2(y-5)=0,
即7x+4y=20.① 又= (x, y ), = (4, ) ,
跟踪训练
3.如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),=, =,AD与BC相交于点M,求点M的坐标.
因为∥,所以x-4(y )=0,
即7x-16y=-20.②
联立①②解得x=,y=2,
故点M的坐标为(, 2).
题型四 共线向量与线段分点坐标的计算
1.设P1,P2的坐标分别是(x1,y1),(x2,y2),如何求线段P1P2的中点P的坐标?
探究问题
提示:如图所示,∵P为P1P2的中点,
∴ ,
∴ - = -,
∴ = (+ )= ,
∴线段P1P2的中点坐标是.
探究问题
2.设P1,P2的坐标分别是(x1,y1),(x2,y2),点P是线段P1P2的一个三等分点,则P点坐标是什么?
提示:点P是线段P1P2的一个三等分点,分两种情况:
①当= 时,
= + = + = + (- )= + = ;
探究问题
2.设P1,P2的坐标分别是(x1,y1),(x2,y2),点P是线段P1P2的一个三等分点,则P点坐标是什么?
②当= 时,
= + = +
= + (- ) = +
= .
3.当=λ时,点P的坐标是什么?
探究问题
提示:∵ = + = +λ = +λ(- )= +λ -λ ,
∴ = = (x1,y1)+ (x2,y2)
= (x1,y1)+ (x2, y2)
= (,)
∴ P (,)
[例4] 已知点A(3, -4)与点B(-1, 2),点P在直线AB上,且||=2||,求点P的坐标.
∴(x-3,y+4)=2(-1-x, 2-y),
∴ 解得
∴P点坐标为(,0).
设P点坐标为(x,y),||=2||.
当P在线段AB上时, =2 ,
[例4] 已知点A(3, -4)与点B(-1, 2),点P在直线AB上,且||=2||,求点P的坐标.
∴(x-3,y+4)=-2(-1-x,2-y),
∴ 解得
∴P点坐标为(-5,8).
当P在线段AB延长线上时, =-2 ,
综上所述,点P的坐标为(,0)或(-5,8).
多维探究
变式1 已知点A(3, -4)与点B(-1, 2),点P在直线AB上,且=3,求点P的坐标.
所以点P的坐标为(0, ).
因为=3,所以(x-3,y+4)=3(-1-x, 2-y),
所以 解得
变式2 若将本例条件改为“经过点P(-2,3)的直线分别交x轴、y轴于点A,B,且||=3||”,求点A,B的坐标.
由题设知,A,B,P三点共线,且||=3||,设A(x,0),B(0,y),
①点P在A,B之间,则有=3 ,
∴(-x,y)=3(-2-x,3),
解得x=-3,y=9,
点A,B的坐标分别为(-3,0),(0,9).
②点P不在A,B之间,则有=-3 ,同理,
可求得点A,B的坐标分别为(,0),(0,-9).
综上,点A,B的坐标分别为(-3,0),(0,9)或(,0) ,(0,-9).
反思感悟
(1)设P1(x1,y1),P2(x2,y2).若点P是P1P2的中点时,则P(x,y)为.
(2)求线段P1P2上或延长线上的点的坐标时,不必过分强调公式的记忆,可以转化为向量问题后列出方程组求解,同时要注意分类讨论.
求点的坐标时注意的问题
(3)若=λ (λ≠0),
①0<λ<1时,P在线段P1P2上;
②λ=1时,P与P2重合;
③λ>1时,点P在线段P1P2延长线上;
④λ<0时,点P在线段P1P2反向延长线上.
随堂检测
1.判断正误
(1)若a=(x1,y1),b=(x2,y2),且a与b共线,则.( )
(2)若a=(x1,y1),b=(x2,y2),且x1y2≠x2y1,则a与b不共线.( )
(3)若A,B,C三点共线,则向量, , 都是共线向量.( )
×
√
√
2.已知两点A(2, -1),B(3, 1),则与平行且方向相反的向量a可以是( )
A.(1,-2) B.(9,3)
C.(-2,4) D.(-4,-8)
由题意,得=(1, 2),所以a=λ =(λ,2λ)(其中λ<0).
符合条件的只有D项.
D
3.已知平面向量a=(1, 2),b=(-2,m),且a∥b,则2a+3b等于____________.
∵a∥b,
∴1×m-(-2)×2=0,
∴m=-4,
∴a=(1, 2),b=(-2,-4),
∴2a+3b=2(1, 2)+3(-2,-4)=(-4,-8).
(-4,-8)
4.设O是坐标原点, =(k,12), =(4,5), =(10,k),当k为何值时,A,B,C三点共线?
∵ = - =(4-k,-7),
= - =(10-k,k-12),
又A,B,C三点共线,
∴由两向量平行,得(4-k)(k-12)+7(10-k)=0,
解得k=-2或k=11.
即当k=-2或k=11时,A,B,C三点共线.
本课小结
已知a=(x1,y1),b=(x2,y2),
(1)当b≠0时,a=λb.
(2) x1y2-x2y1=0.
(3)当x2y2≠0时, ,即两向量的相应坐标成比例.
1.两个向量共线条件的表示方法
本课小结
两向量共线的坐标表示的应用,可分为两个方面.
(1)已知两个向量的坐标判定两向量共线.联系平面几何平行、共线知识,可以证明三点共线、直线平行等几何问题.要注意区分向量的共线、平行与几何中的共线、平行的不同.
(2)已知两个向量共线,求点或向量的坐标,求参数的值,求轨迹方程,要注意方程思想的应用,向量共线的条件,向量相等的条件等都可作为列方程的依据.
2.向量共线的坐标表示的应用
通过本节课,你学会了什么?
6.3.4 平面向量数乘运算的坐标表示
高一
必修二
本节目标
1.掌握向量数乘的坐标运算法则.
2.理解用坐标表示两向量共线的条件.
3.能根据平面向量的坐标,判断向量是否共线,并掌握三点共线的判断方法.
课前预习
预习课本P31~33,思考并完成以下问题
如何由a的坐标求λa的坐标?
(2) 如何利用向量的坐标运算表示两个向量共线?
课前小测
1.已知向量=(2, 4), =(0,2),则=( )
A.(-2, -2) B.(2, 2)
C.(1, 1) D.(-1, -1)
=
=
=
=
D
2.下列各对向量中,共线的是( )
A.a=(2, 3),b=(3, -2)
B.a=(2, 3),b=(4, -6)
C.a=(, -1),b=(1, )
D.a=(1, ),b=(, 2)
不共线
不共线
不共线
共线
b=a
D
3.已知a=(-3, 2),b=(6,y),且a∥b,则y=________.
y=-4
-4
4.若A(3, -6),B(-5, 2),C(6, y)三点共线,则y=_______.
∴-8(y+6)-8×3=0,解得y=-9.
=(-8, 8), =(3,y+6),
∵A,B,C三点共线,即∥ ,
-9
新知探究
已知a=(x,y),则λa=λ(x,y)=__________.
1.数乘运算的坐标表示
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
(1)符号表示
(λx,λy)
(2)文字描述
(2)如果用坐标表示,向量a,b(b≠0)共线的充要条件是______________.
2.平面向量共线的坐标表示
(1)设a=(x1,y1),b=(x2,y2),其中b≠0,a,b共线的充要条件是存在实数λ,使a=λb.
x1y2-x2y1=0
两向量a=(x1,y1),b=(x2,y2)共线的坐标条件能表示成吗?
思考
提示: 不一定,x2,y2有一者为零时,比例式没有意义,只有x2y2≠0时,才能使用.
题型突破
典例深度剖析 重点多维探究
题型一 向量共线的判定与证明
[例1] (1)下列各组向量中,共线的是( )
A.a=(-2, 3),b=(4, 6)
B.a=(2, 3),b=(3, 2)
C.a=(1, -2),b=(7, 14)
D.a=(-3, 2),b=(6, -4)
利用“纵横交错积相减”判断.
-2×6-3×4 ≠ 0
3×3-2×2 ≠ 0
1×14-(-2)×7≠0
(-3)×(-4)-2×6=0
D
(2)已知A(-1,-1),B(1,3),C(1,5),D(2,7),向量与平行吗?直线AB平行于直线CD吗?
∵ =(1-(-1),3-(-1))=(2,4),=(2-1,7-5)=(1,2).
又2×2-4×1=0,
∴ ∥ .
又=(2,6), =(2,4),
∴2×4-2×6≠0,
∴A,B,C不共线,
∴AB与CD不重合,
∴AB∥CD.
方法总结
向量共线的判定方法
提醒:向量共线的坐标表达式极易写错,如写成x1y1-x2y2=0或x1x2-y1y2=0都是不对的,因此要理解并记熟这一公式,可简记为:纵横交错积相减.
跟踪训练
1.已知A(1,-3),B (8, ) ,C(9,1),求证:A,B,C三点共线.
=(8-1, +3)= (7, ) , =(9-1,1+3)=(8,4),
∵7×4- ×8=0,
∴ ∥,且,有公共点A,
∴A,B,C三点共线.
题型二 已知平面向量共线求参数
[例2] 已知a=(1, 2),b=(-3, 2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?
法一:可利用b与非零向量a共线等价于b=λa(λ>0,b与a同向;λ<0,b与a反向)求解;
法二:可先利用坐标形式的等价条件求k,再利用b=λa判定同向还是反向.
!
思路探究
[例2] 已知a=(1, 2),b=(-3, 2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?
ka+b=k(1, 2)+(-3, 2)=(k-3, 2k+2),
a-3b=(1, 2)-3(-3, 2)=(10, -4),
当ka+b与a-3b平行时,存在唯一实数λ,使ka+b=λ(a-3b).
由(k-3, 2k+2)=λ(10, -4),
法一:(共线向量定理法)
所以
当k=-时,ka+b与a-3b平行,这时ka+b=-a+b=-(a-3b),
因为λ=-<0,所以ka+b与a-3b反向.
解得k=λ=-.
[例2] 已知a=(1, 2),b=(-3, 2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?
由题知ka+b=(k-3, 2k+2),a-3b=(10,-4),
因为ka+b与a-3b平行,
所以(k-3)×(-4)-10×(2k+2)=0,
解得k=-.
这时ka+b= (--3, -+2) =- (a-3b),
所以当k=-时,ka+b与a-3b平行,并且反向.
法二:(坐标法)
反思感悟
(1)利用共线向量定理a=λb(b≠0)列方程组求解.
(2)利用向量平行的坐标表达式x1y2-x2y1=0直接求解.
利用向量平行的条件处理求值问题的思路
跟踪训练
2.已知向量a=(1, 2),b=(2, -2),c=(1, λ),若c∥(2a+b),则λ=________.
λ=
2a+b=(4, 2)
c∥(2a+b),c=(1,λ)
4λ-2=0
题型三 向量共线的综合应用
[例3] (1)已知向量a=(cosα, -2),b=(sinα, 1),且a∥b,则2sinαcosα等于( )
A.3 B.-3
C.- D.
所以2sinαcosα= = ==-.
因为a∥b,所以cos α×1-(-2)×sin α=0,
即cosα=-2sin α,tanα=- ,
C
(2)如图所示,已知点A(4,0),B(4,4),C(2,6),求AC与OB的交点P的坐标.
由O,P,B三点共线,可设=λ=(4λ,4λ),
则=-=(4λ-4, 4λ),
= -=(-2, 6).
由与共线得(4λ-4)×6-4λ×(-2)=0,解得λ=,所以= =(3,3),所以P点的坐标为(3,3).
法一:(定理法)
(2)如图所示,已知点A(4,0),B(4,4),C(2,6),求AC与OB的交点P的坐标.
设P(x,y),则=(x,y),因为=(4,4),且与共线,所以,即x=y.
又=(x-4,y), =(-2,6),
且与共线,则(x-4)×6-y×(-2)=0,解得x=y=3,所以P点的坐标为(3,3).
法二:(坐标法)
方法总结
应用向量共线的坐标表示求解几何问题的步骤
跟踪训练
3.如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),=, =,AD与BC相交于点M,求点M的坐标.
因为= = (0,5)=(0, ),所以C (0, ).
因为= = (4,3)= (2, ) ,所以D (2, ).
设M(x,y),则=(x,y-5),
= (2-0, 5)= (2, ).
因为∥ ,所以-x-2(y-5)=0,
即7x+4y=20.① 又= (x, y ), = (4, ) ,
跟踪训练
3.如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),=, =,AD与BC相交于点M,求点M的坐标.
因为∥,所以x-4(y )=0,
即7x-16y=-20.②
联立①②解得x=,y=2,
故点M的坐标为(, 2).
题型四 共线向量与线段分点坐标的计算
1.设P1,P2的坐标分别是(x1,y1),(x2,y2),如何求线段P1P2的中点P的坐标?
探究问题
提示:如图所示,∵P为P1P2的中点,
∴ ,
∴ - = -,
∴ = (+ )= ,
∴线段P1P2的中点坐标是.
探究问题
2.设P1,P2的坐标分别是(x1,y1),(x2,y2),点P是线段P1P2的一个三等分点,则P点坐标是什么?
提示:点P是线段P1P2的一个三等分点,分两种情况:
①当= 时,
= + = + = + (- )= + = ;
探究问题
2.设P1,P2的坐标分别是(x1,y1),(x2,y2),点P是线段P1P2的一个三等分点,则P点坐标是什么?
②当= 时,
= + = +
= + (- ) = +
= .
3.当=λ时,点P的坐标是什么?
探究问题
提示:∵ = + = +λ = +λ(- )= +λ -λ ,
∴ = = (x1,y1)+ (x2,y2)
= (x1,y1)+ (x2, y2)
= (,)
∴ P (,)
[例4] 已知点A(3, -4)与点B(-1, 2),点P在直线AB上,且||=2||,求点P的坐标.
∴(x-3,y+4)=2(-1-x, 2-y),
∴ 解得
∴P点坐标为(,0).
设P点坐标为(x,y),||=2||.
当P在线段AB上时, =2 ,
[例4] 已知点A(3, -4)与点B(-1, 2),点P在直线AB上,且||=2||,求点P的坐标.
∴(x-3,y+4)=-2(-1-x,2-y),
∴ 解得
∴P点坐标为(-5,8).
当P在线段AB延长线上时, =-2 ,
综上所述,点P的坐标为(,0)或(-5,8).
多维探究
变式1 已知点A(3, -4)与点B(-1, 2),点P在直线AB上,且=3,求点P的坐标.
所以点P的坐标为(0, ).
因为=3,所以(x-3,y+4)=3(-1-x, 2-y),
所以 解得
变式2 若将本例条件改为“经过点P(-2,3)的直线分别交x轴、y轴于点A,B,且||=3||”,求点A,B的坐标.
由题设知,A,B,P三点共线,且||=3||,设A(x,0),B(0,y),
①点P在A,B之间,则有=3 ,
∴(-x,y)=3(-2-x,3),
解得x=-3,y=9,
点A,B的坐标分别为(-3,0),(0,9).
②点P不在A,B之间,则有=-3 ,同理,
可求得点A,B的坐标分别为(,0),(0,-9).
综上,点A,B的坐标分别为(-3,0),(0,9)或(,0) ,(0,-9).
反思感悟
(1)设P1(x1,y1),P2(x2,y2).若点P是P1P2的中点时,则P(x,y)为.
(2)求线段P1P2上或延长线上的点的坐标时,不必过分强调公式的记忆,可以转化为向量问题后列出方程组求解,同时要注意分类讨论.
求点的坐标时注意的问题
(3)若=λ (λ≠0),
①0<λ<1时,P在线段P1P2上;
②λ=1时,P与P2重合;
③λ>1时,点P在线段P1P2延长线上;
④λ<0时,点P在线段P1P2反向延长线上.
随堂检测
1.判断正误
(1)若a=(x1,y1),b=(x2,y2),且a与b共线,则.( )
(2)若a=(x1,y1),b=(x2,y2),且x1y2≠x2y1,则a与b不共线.( )
(3)若A,B,C三点共线,则向量, , 都是共线向量.( )
×
√
√
2.已知两点A(2, -1),B(3, 1),则与平行且方向相反的向量a可以是( )
A.(1,-2) B.(9,3)
C.(-2,4) D.(-4,-8)
由题意,得=(1, 2),所以a=λ =(λ,2λ)(其中λ<0).
符合条件的只有D项.
D
3.已知平面向量a=(1, 2),b=(-2,m),且a∥b,则2a+3b等于____________.
∵a∥b,
∴1×m-(-2)×2=0,
∴m=-4,
∴a=(1, 2),b=(-2,-4),
∴2a+3b=2(1, 2)+3(-2,-4)=(-4,-8).
(-4,-8)
4.设O是坐标原点, =(k,12), =(4,5), =(10,k),当k为何值时,A,B,C三点共线?
∵ = - =(4-k,-7),
= - =(10-k,k-12),
又A,B,C三点共线,
∴由两向量平行,得(4-k)(k-12)+7(10-k)=0,
解得k=-2或k=11.
即当k=-2或k=11时,A,B,C三点共线.
本课小结
已知a=(x1,y1),b=(x2,y2),
(1)当b≠0时,a=λb.
(2) x1y2-x2y1=0.
(3)当x2y2≠0时, ,即两向量的相应坐标成比例.
1.两个向量共线条件的表示方法
本课小结
两向量共线的坐标表示的应用,可分为两个方面.
(1)已知两个向量的坐标判定两向量共线.联系平面几何平行、共线知识,可以证明三点共线、直线平行等几何问题.要注意区分向量的共线、平行与几何中的共线、平行的不同.
(2)已知两个向量共线,求点或向量的坐标,求参数的值,求轨迹方程,要注意方程思想的应用,向量共线的条件,向量相等的条件等都可作为列方程的依据.
2.向量共线的坐标表示的应用
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
