人教版(2019)数学必修第二册6.4 解三角形应用举例 课件(共45张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册6.4 解三角形应用举例 课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 10:58:51 | ||
图片预览







文档简介
(共45张PPT)
6.4 解三角形应用举例
考纲分析
课程标准解读 关联考点 核心素养
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题. 1.解三角形的实际应用. 2.正、余弦定理在平面几何中的应用. 3.解三角形与三角函数的综合问题. 1.数学建模.
2.直观想象.
3.数学运算.
课前自测
(4)方位角大小的范围是[0,2π),方向角大小的范围一般是.( )
1.判断正误(正确的打“√”,错误的打“×”)
(1)从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为α+β=180°.( )
(2)俯角是铅垂线与视线所成的角,其范围为.( )
(3)方位角与方向角其实质是一样的,均是确定观察点与目标点之间的位置关系.( )
×
×
√
√
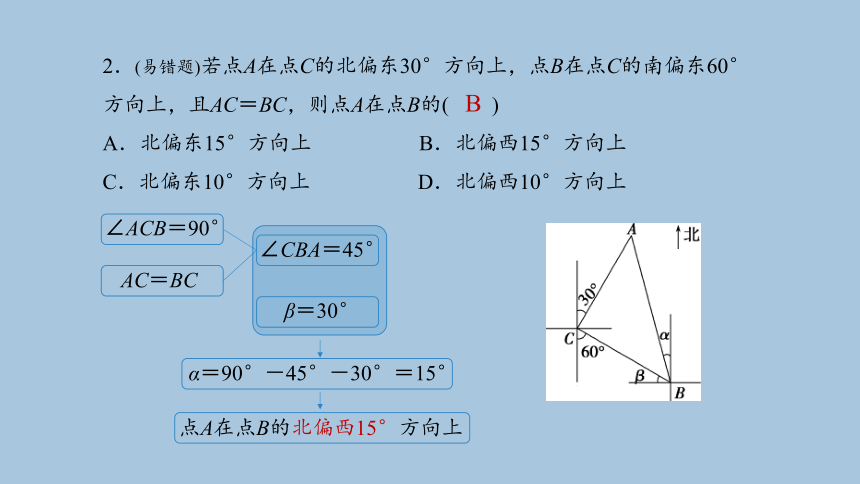
2.(易错题)若点A在点C的北偏东30°方向上,点B在点C的南偏东60°方向上,且AC=BC,则点A在点B的( )
A.北偏东15°方向上 B.北偏西15°方向上
C.北偏东10°方向上 D.北偏西10°方向上
∠ACB=90°
AC=BC
∠CBA=45°
β=30°
α=90°-45°-30°=15°
点A在点B的北偏西15°方向上
B
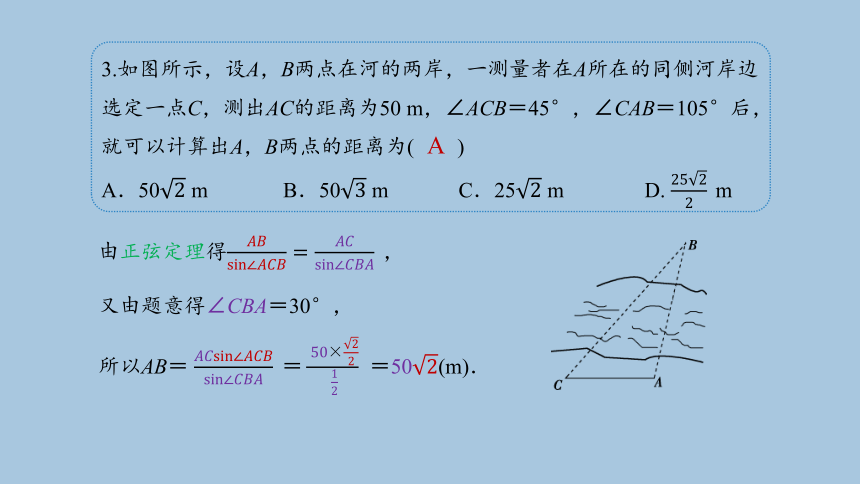
3.如图所示,设A,B两点在河的两岸,一测量者在A所在的同侧河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
A.50 m B.50 m C.25 m D. m
所以AB= = =50(m).
由正弦定理得,
又由题意得∠CBA=30°,
A
4.如图所示,D,C,B三点在地面的同一条直线上,DC=a,从C,D两点测得A点的仰角分别为60°,30°,则A点离地面的高度AB=________.
∠ACB=60°
∠ADC=30°
∠DAC=30°
△ADC为等腰三角形
AD=a
AB= AD= a
a
5.在一次抗洪抢险中,某救生艇发动机突然发生故障停止转动,失去动力的救生艇在洪水中漂行,此时,风向是北偏东30°,风速是20 km/h;水的流向是正东,流速是20 km/h,若不考虑其他因素,救生艇在洪水中漂行的速度的方向为北偏东________,大小为________km/h.
∠COY=30°+30°=60°.
如图,∠AOB=60°,
由余弦定理知OC2=202+202-800cos120°=1200,
故OC=20,
60°
20
考点梳理
1.仰角和俯角
在目标视线和水平视线所成的角中,目标视线在水平视线上方的角叫仰角,在水平视线下方的角叫俯角(如图).
铅垂线
水平线
视线
视线
仰角
俯角
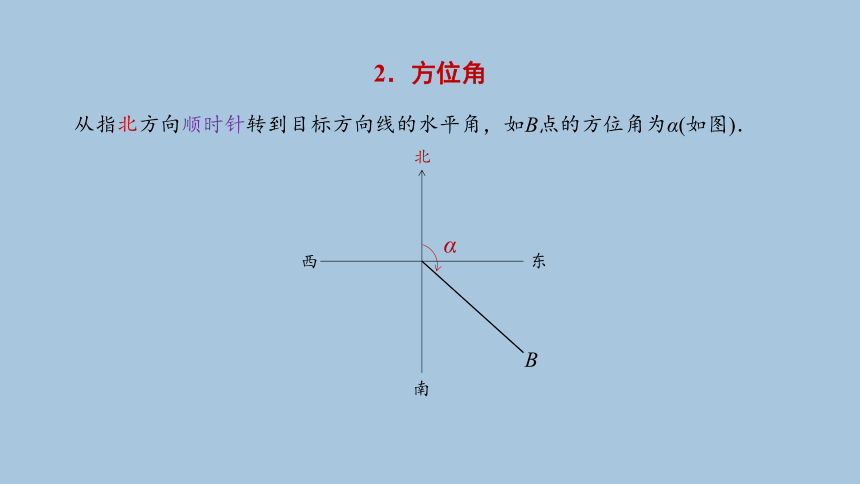
2.方位角
从指北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图).
北
南
东
西
B
α
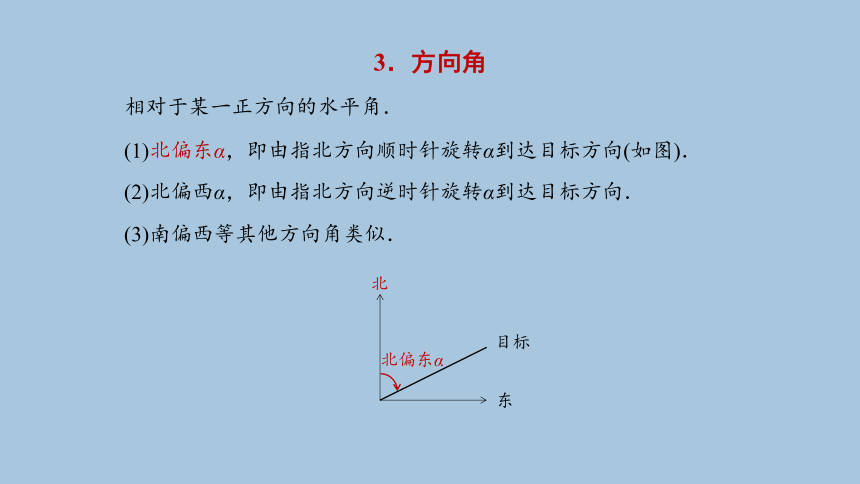
3.方向角
相对于某一正方向的水平角.
(3)南偏西等其他方向角类似.
(2)北偏西α,即由指北方向逆时针旋转α到达目标方向.
(1)北偏东α,即由指北方向顺时针旋转α到达目标方向(如图).
北
东
目标
北偏东α
常见误区
1.仰角与俯角是相对水平视线而言,而方位角是相对于正北方向而言的.
!
2.“方位角”与“方向角”的区别:方位角大小的范围是[0,2π),方向角大小的范围是.
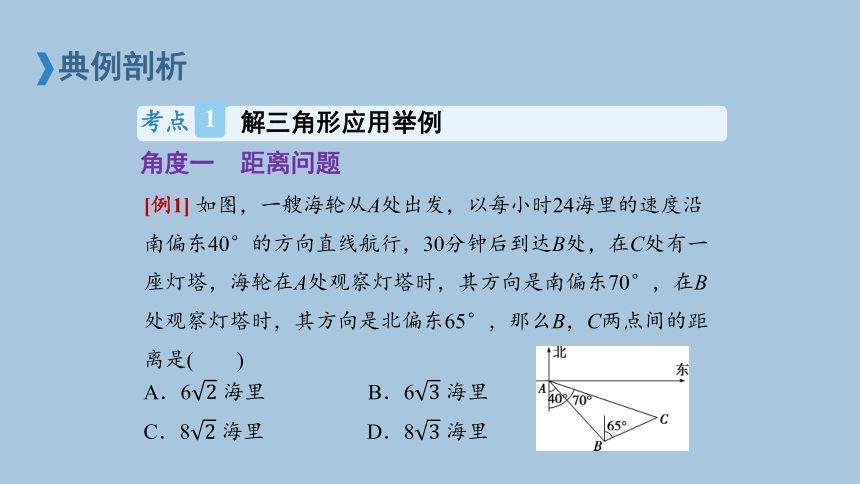
[例1] 如图,一艘海轮从A处出发,以每小时24海里的速度沿南偏东40°的方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔时,其方向是南偏东70°,在B处观察灯塔时,其方向是北偏东65°,那么B,C两点间的距离是( )
A.6 海里 B.6 海里
C.8 海里 D.8 海里
典例剖析
考点
1
解三角形应用举例
角度一 距离问题
过点C向正南方向作一条射线CD,如图所示.
由题意可知,∠BAC=70°-40°=30°,∠ACD=110°,
所以∠ACB=110°-65°=45°.
[例1] 如图,一艘海轮从A处出发,以每小时24海里的速度沿南偏东40°的方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔时,其方向是南偏东70°,在B处观察灯塔时,其方向是北偏东65°,那么B,C两点间的距离是( )
A.6 海里 B.6 海里 C.8 海里 D.8 海里
AB=24×0.5=12(海里).
在△ABC中,由正弦定理得,即,
所以BC=6海里.
A
方法总结
(1)选定或确定要创建的三角形,首先确定所求量所在的三角形,若其他量已知则直接求解;若有未知量,则把未知量放在另一个确定的三角形中求解.
(2)确定用正弦定理还是余弦定理,如都可以用,就选便于计算的定理,选定合适的三角形.
解决距离问题的两个注意事项
角度一 高度问题
[例2] 2019年10月1日,在庆祝中华人民共和国成立70周年阅兵中,由我国自主研制的军用飞机和军用无人机等参阅航空装置分秒不差飞越天安门,壮军威,振民心,令世人瞩目,飞行员高超的飞机技术离不开艰苦的训练和科学的数据分析.一次飞行训练中,地面观测站观测到一架参阅直升飞机以72 km/h的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西60°的方向上,1 min后第二次观测到该飞机在北偏东75°的方向上,仰角为30°,则直升飞机飞行的高度为________km.(结果保留根号).
所以AB= AE+BE=(2+2)x=,
即直升飞机飞行的高度为 km.
如图,过点O作AB的垂线,垂足为E.
由题意知∠EOA=60°,∠EOB=75°,∠COB=30°,AB= = .
设OE=x,则AE=xtan∠EOA= x,
BE=xtan∠EOB=xtan(45°+30°)=x· =(2+)x,
解得x=,
所以OB== = × =,
所以BC=OBtan∠COB=×= ,
方法总结
②在实际问题中可能会遇到空间与平面(底面)同时研究的问题,这时最好画两个图形,一个空间图形,一个平面图形;
解决高度问题的三个注意事项
①要理解仰角、俯角的定义;
③注意山或塔垂直底面或海平面,把空间问题转化为平面问题.
角度三 角度问题
在△ABD中,B=45°,
由正弦定理得,
AD= =24.
在△ACD中,由余弦定理得CD2=AC2+AD2-2AC×AD×cos 30°,
因为AC=12,AD=24,所以CD=12,
由正弦定理得,sin∠CDA=,
故∠CDA=60°或者∠CDA=120°.
因为AD>AC,故∠CDA为锐角,所以∠CDA=60°.
[例3] 一艘游轮航行到A处时看灯塔B在A的北偏东75°,距离为12海里,灯塔C在A的北偏西30°,距离为12 海里,该游轮由A沿正北方向继续航行到D处时再看灯塔B在其南偏东60°方向,则此时灯塔C位于游轮的( )
A.正西方向 B.南偏西75°方向
C.南偏西60°方向 D.南偏西45°方向
C
方法总结
(1)测量角度时,首先应明确方位角及方向角的含义;
(3)在解应用题时,要根据题意正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题,解题过程中也要注意体会正、余弦定理综合使用的优点.
(2)求角的大小时,先在三角形中求出其正弦或余弦值;
解决角度问题的三个注意事项
跟踪训练
一艘海轮从A出发,沿北偏东75°的方向航行(2-2)n mile到达海岛B,然后从B出发,沿北偏东15°的方向航行4 n mile到达海岛C.
(1)求AC的长;
(2)如果下次航行直接从A出发到达C,求∠CAB的大小.
所以AC=2.
由题意,在△ABC中,∠ABC=180°-75°+15°=120°,
AB=2-2,BC=4,
根据余弦定理得
AC2=AB2+BC2-2AB×BC×cos∠ABC
=(2-2)2+42+(2-2)×4
=24
一艘海轮从A出发,沿北偏东75°的方向航行(2-2)n mile到达海岛B,然后从B出发,沿北偏东15°的方向航行4 n mile到达海岛C.
(1)求AC的长;
一艘海轮从A出发,沿北偏东75°的方向航行(2-2)n mile到达海岛B,然后从B出发,沿北偏东15°的方向航行4 n mile到达海岛C.
(2)如果下次航行直接从A出发到达C,求∠CAB的大小.
所以∠CAB=45°.
根据正弦定理得,
sin∠BAC= = ,
考点
2
平面图形中的计算问题
[例4] 在△ABC中,角A,B,C的对边分别为a,b,c.已知a=3,c=,B=45°.
(1)求sin C的值;
(2)在边BC上取一点D,使得cos∠ADC=-,求tan∠DAC的值.
[例4] 在△ABC中,角A,B,C的对边分别为a,b,c.已知a=3,c=,B=45°.
(1)求sin C的值;
在△ABC中,因为a=3,c=,B=45°,
由余弦定理b2=a2+c2-2accos B,
得b2=9 +2-2×3× cos 45°=5,
所以b= .
在△ABC中,由正弦定理,得,
所以sin C= .
[例4] 在△ABC中,角A,B,C的对边分别为a,b,c.已知a=3,c=,B=45°.
(2)在边BC上取一点D,使得cos∠ADC=-,求tan∠DAC的值.
在△ADC中,因为cos∠ADC=-,所以∠ADC为钝角,
而∠ADC+C+∠CAD= 180°,所以C为锐角.
故cos C= = ,则tan C= = .
因为cos ∠ADC=-,所以sin ∠ADC= = ,
tan ∠ADC= =-,
从而tan ∠DAC=tan(180°-∠ADC-C)=-tan(∠ADC+C)
=- =- = .
方法总结
具体解题思路如下:
(1)把所提供的平面图形拆分成若干个三角形,然后在各个三角形内利用正弦、余弦定理求解;
(2)寻找各个三角形之间的联系,交叉使用公共条件,求出结果.
求解平面图形中的计算问题,关键是梳理条件和所求问题的类型,然后将数据化归到三角形中,利用正弦定理或余弦定理建立已知和所求的关系.
与平面图形有关的解三角形问题的关键及思路
跟踪训练
如图,在平面四边形ABCD中,∠ACB与∠D互补,cos∠ACB= ,AC=BC=2,AB=4AD.
(1)求AB的长;
(2)求sin∠ACD.
所以AB=4.
如图,在平面四边形ABCD中,∠ACB与∠D互补,cos∠ACB= ,AC=BC=2,AB=4AD.
(1)求AB的长;
由余弦定理AB2=BC2+AC2-2AC·BCcos∠ACB,
得AB2=(2)2+(2)2-2×2×2×=16,
如图,在平面四边形ABCD中,∠ACB与∠D互补,cos∠ACB= ,AC=BC=2,AB=4AD.
(2)求sin∠ACD.
因为AB=4且AB=4AD,所以AD=1,
因为∠ACB与∠D互补,所以cos D=-cos∠ACB=-,
所以sin D= = ,
由正弦定理,得sin∠ACD= .
考点
3
正、余弦定理与其他知识的交汇
[例5] 已知△ABC的内角A,B,C的对边分别为a,b,c,________,若b=,________.
请从下面的三个条件中任选一个,两个结论中任选一个,组成一个完整的问题,并给出解答.
条件:①asin=bsin A,
②bsin A=acos,
③a2+c2-b2=abcos A+a2cos B.
结论:①求△ABC周长的取值范围;
②求△ABC面积的最大值.
则由正弦定理得sin Asin =sin Bsin A,
因为sin A≠0,所以sin =sin B.
由A+B+C=π,可得sin =cos . 故cos =2sin cos .
在△ABC中,由正弦定理,可得bsin A=asin B,
又bsin A=acos,
所以asin B=acos,即sin B=cos .
所以sin B= cos B+ sin B,可得tan B= .
选择条件①
因为cos ≠0,故sin = .
又因为B∈(0,π),所以B= .
选择条件②
又B∈(0,π),所以B= .
因为a2+c2-b2=abcos A+a2cos B,
所以由余弦定理,得2accos B=abcos A+a2cos B,
又a≠0,所以2ccos B=bcos A+acos B.
由正弦定理得2sin Ccos B=sin Bcos A+sin Acos B=sin(A+B)=sin C.
选择条件③
又C∈(0,π),所以sin C>0,所以cos B= .
因为B∈(0,π),所以B=.
解得a+c≤2(当且仅当a=c=时,等号成立).
又a+c>b=,所以2选择结论①
因为b=.
所以由余弦定理得13=a2+c2-2accos B=a2+c2-ac=(a+c)2-3ac,
所以(a+c)2=13+3ac≤13+3 ,
故△ABC的周长的取值范围为(2,3 ].
因为b=,
所以由余弦定理结合基本不等式得13=a2+c2-2accos B=a2+c2-ac≥2ac-ac=ac(当且仅当a=c=时,等号成立).
所以△ABC的面积S= acsin B≤ × = ,
即△ABC的面积的最大值为.
选择结论②
方法总结
解答本题的关键是注意到三角形面积公式S△ABC= acsin B中的ac,与余弦定理中的a2+c2存在不等关系a2+c2≥2ac,利用余弦定理沟通二者,求出ac的最值即可.
关键点拨
跟踪训练
在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且.
(1)求角C的大小;
(2)若b=1,求c的取值范围.
在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且.
(1)求角C的大小;
因为,
所以b=ccos A+asin C,
由正弦定理得,sin B=sin Ccos A+sin Asin C,
又sin B=sin(A+C)=sin Acos C+cos Asin C.
所以sin Asin C=sin Acos C,
又0在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且.
(2)若b=1,求c的取值范围.
由(1)可知,A+B= ,又△ABC是锐角三角形,
所以 得所以由正弦定理,得c= ·sin C= ,所以c∈ .
随堂检测
1.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD. 已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
A.50 米 B.50 米 C.50米 D.50米
设该扇形的半径为r米,连接CO.
由题意,得CD=150(米),OD=100(米),∠CDO=60°,
在△CDO中,CD2+OD2-2CD·OD·cos 60°=OC2,
即1502+1002-2×150×100×=r2,
解得r=50 .
B
所以AB=1+tan 30°·CB=1+20(米).
2.某工厂实施煤改电工程防治雾霾,欲拆除高为AB的烟囱,测绘人员取与烟囱底部B在同一水平面内的两个观测点C,D,测得∠BCD=75°,∠BDC=60°,CD=40米,并在点C处的正上方E处观测顶部A的仰角为30°,且CE=1米,则烟囱高AB=________米.
∠CBD=180°-∠BCD-∠BDC=45°,
在△CBD中,由正弦定理得BC= =20(米),
1+20
所以此船的航行速度v= = (海里/时).
3.一船自西向东匀速航行,上午10时到达灯塔P的南偏西75°,距灯塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则此船航行的速度为________海里/时.
如图,由题意知∠MPN=75°+45°=120°,∠PNM=45°.
在△PMN中,由正弦定理得,
所以MN=68× =34(海里).
又由M到N所用的时间为14-10=4(小时),
4.在△ABC中,内角A,B,C所对的边分别为a,b,c,若sin Asin Bcos C=sin2C,则=________,sin C的最大值为________.
又cos2C+sin2C=1,所以sin2C=1-cos2C≤ ,sin C≤ .
由题意结合正弦定理知abcos C=c2,即cos C=,
又cos C=,所以a2+b2-c2=2c2,得a2+b2=3c2,即=3.
故cos C== =≥ =,
当且仅当a=b时取等号,
3
因为(2a-c)cos B-bcos C=0,
所以2acos B-ccos B-bcos C=0,
由正弦定理得2sin Acos B-sin Ccos B-cos Csin B=0,
即2sin Acos B-sin(C+B)=0,
又C+B=π-A,所以sin(C+B)=sin A.
所以sin A(2cos B-1)=0.
在△ABC中,sin A≠0,
所以cos B= ,又B∈(0,π),所以B= .
5.在△ABC中,a,b,c分别是角A,B,C的对边,(2a-c)·cos B-bcos C=0.
(1)求角B的大小;
5.在△ABC中,a,b,c分别是角A,B,C的对边,(2a-c)·cos B-bcos C=0.
(2)设函数f(x)=2sin xcos xcos B- cos 2x,求函数f(x)的最大值及当f(x)取得最大值时x的值.
即当x=kπ+ (k∈Z)时,f(x)取得最大值1.
因为B= ,所以f(x)= sin 2x- cos 2x=sin ,
令2x- =2kπ+ (k∈Z),得x=kπ+(k∈Z),
本课小结
测量距离问题,测量高度问题,测量角度问题,是高考考查的热点,题型各种类型都有,难度中等.
6.4 解三角形应用举例
考纲分析
课程标准解读 关联考点 核心素养
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题. 1.解三角形的实际应用. 2.正、余弦定理在平面几何中的应用. 3.解三角形与三角函数的综合问题. 1.数学建模.
2.直观想象.
3.数学运算.
课前自测
(4)方位角大小的范围是[0,2π),方向角大小的范围一般是.( )
1.判断正误(正确的打“√”,错误的打“×”)
(1)从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为α+β=180°.( )
(2)俯角是铅垂线与视线所成的角,其范围为.( )
(3)方位角与方向角其实质是一样的,均是确定观察点与目标点之间的位置关系.( )
×
×
√
√
2.(易错题)若点A在点C的北偏东30°方向上,点B在点C的南偏东60°方向上,且AC=BC,则点A在点B的( )
A.北偏东15°方向上 B.北偏西15°方向上
C.北偏东10°方向上 D.北偏西10°方向上
∠ACB=90°
AC=BC
∠CBA=45°
β=30°
α=90°-45°-30°=15°
点A在点B的北偏西15°方向上
B
3.如图所示,设A,B两点在河的两岸,一测量者在A所在的同侧河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
A.50 m B.50 m C.25 m D. m
所以AB= = =50(m).
由正弦定理得,
又由题意得∠CBA=30°,
A
4.如图所示,D,C,B三点在地面的同一条直线上,DC=a,从C,D两点测得A点的仰角分别为60°,30°,则A点离地面的高度AB=________.
∠ACB=60°
∠ADC=30°
∠DAC=30°
△ADC为等腰三角形
AD=a
AB= AD= a
a
5.在一次抗洪抢险中,某救生艇发动机突然发生故障停止转动,失去动力的救生艇在洪水中漂行,此时,风向是北偏东30°,风速是20 km/h;水的流向是正东,流速是20 km/h,若不考虑其他因素,救生艇在洪水中漂行的速度的方向为北偏东________,大小为________km/h.
∠COY=30°+30°=60°.
如图,∠AOB=60°,
由余弦定理知OC2=202+202-800cos120°=1200,
故OC=20,
60°
20
考点梳理
1.仰角和俯角
在目标视线和水平视线所成的角中,目标视线在水平视线上方的角叫仰角,在水平视线下方的角叫俯角(如图).
铅垂线
水平线
视线
视线
仰角
俯角
2.方位角
从指北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图).
北
南
东
西
B
α
3.方向角
相对于某一正方向的水平角.
(3)南偏西等其他方向角类似.
(2)北偏西α,即由指北方向逆时针旋转α到达目标方向.
(1)北偏东α,即由指北方向顺时针旋转α到达目标方向(如图).
北
东
目标
北偏东α
常见误区
1.仰角与俯角是相对水平视线而言,而方位角是相对于正北方向而言的.
!
2.“方位角”与“方向角”的区别:方位角大小的范围是[0,2π),方向角大小的范围是.
[例1] 如图,一艘海轮从A处出发,以每小时24海里的速度沿南偏东40°的方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔时,其方向是南偏东70°,在B处观察灯塔时,其方向是北偏东65°,那么B,C两点间的距离是( )
A.6 海里 B.6 海里
C.8 海里 D.8 海里
典例剖析
考点
1
解三角形应用举例
角度一 距离问题
过点C向正南方向作一条射线CD,如图所示.
由题意可知,∠BAC=70°-40°=30°,∠ACD=110°,
所以∠ACB=110°-65°=45°.
[例1] 如图,一艘海轮从A处出发,以每小时24海里的速度沿南偏东40°的方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔时,其方向是南偏东70°,在B处观察灯塔时,其方向是北偏东65°,那么B,C两点间的距离是( )
A.6 海里 B.6 海里 C.8 海里 D.8 海里
AB=24×0.5=12(海里).
在△ABC中,由正弦定理得,即,
所以BC=6海里.
A
方法总结
(1)选定或确定要创建的三角形,首先确定所求量所在的三角形,若其他量已知则直接求解;若有未知量,则把未知量放在另一个确定的三角形中求解.
(2)确定用正弦定理还是余弦定理,如都可以用,就选便于计算的定理,选定合适的三角形.
解决距离问题的两个注意事项
角度一 高度问题
[例2] 2019年10月1日,在庆祝中华人民共和国成立70周年阅兵中,由我国自主研制的军用飞机和军用无人机等参阅航空装置分秒不差飞越天安门,壮军威,振民心,令世人瞩目,飞行员高超的飞机技术离不开艰苦的训练和科学的数据分析.一次飞行训练中,地面观测站观测到一架参阅直升飞机以72 km/h的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西60°的方向上,1 min后第二次观测到该飞机在北偏东75°的方向上,仰角为30°,则直升飞机飞行的高度为________km.(结果保留根号).
所以AB= AE+BE=(2+2)x=,
即直升飞机飞行的高度为 km.
如图,过点O作AB的垂线,垂足为E.
由题意知∠EOA=60°,∠EOB=75°,∠COB=30°,AB= = .
设OE=x,则AE=xtan∠EOA= x,
BE=xtan∠EOB=xtan(45°+30°)=x· =(2+)x,
解得x=,
所以OB== = × =,
所以BC=OBtan∠COB=×= ,
方法总结
②在实际问题中可能会遇到空间与平面(底面)同时研究的问题,这时最好画两个图形,一个空间图形,一个平面图形;
解决高度问题的三个注意事项
①要理解仰角、俯角的定义;
③注意山或塔垂直底面或海平面,把空间问题转化为平面问题.
角度三 角度问题
在△ABD中,B=45°,
由正弦定理得,
AD= =24.
在△ACD中,由余弦定理得CD2=AC2+AD2-2AC×AD×cos 30°,
因为AC=12,AD=24,所以CD=12,
由正弦定理得,sin∠CDA=,
故∠CDA=60°或者∠CDA=120°.
因为AD>AC,故∠CDA为锐角,所以∠CDA=60°.
[例3] 一艘游轮航行到A处时看灯塔B在A的北偏东75°,距离为12海里,灯塔C在A的北偏西30°,距离为12 海里,该游轮由A沿正北方向继续航行到D处时再看灯塔B在其南偏东60°方向,则此时灯塔C位于游轮的( )
A.正西方向 B.南偏西75°方向
C.南偏西60°方向 D.南偏西45°方向
C
方法总结
(1)测量角度时,首先应明确方位角及方向角的含义;
(3)在解应用题时,要根据题意正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题,解题过程中也要注意体会正、余弦定理综合使用的优点.
(2)求角的大小时,先在三角形中求出其正弦或余弦值;
解决角度问题的三个注意事项
跟踪训练
一艘海轮从A出发,沿北偏东75°的方向航行(2-2)n mile到达海岛B,然后从B出发,沿北偏东15°的方向航行4 n mile到达海岛C.
(1)求AC的长;
(2)如果下次航行直接从A出发到达C,求∠CAB的大小.
所以AC=2.
由题意,在△ABC中,∠ABC=180°-75°+15°=120°,
AB=2-2,BC=4,
根据余弦定理得
AC2=AB2+BC2-2AB×BC×cos∠ABC
=(2-2)2+42+(2-2)×4
=24
一艘海轮从A出发,沿北偏东75°的方向航行(2-2)n mile到达海岛B,然后从B出发,沿北偏东15°的方向航行4 n mile到达海岛C.
(1)求AC的长;
一艘海轮从A出发,沿北偏东75°的方向航行(2-2)n mile到达海岛B,然后从B出发,沿北偏东15°的方向航行4 n mile到达海岛C.
(2)如果下次航行直接从A出发到达C,求∠CAB的大小.
所以∠CAB=45°.
根据正弦定理得,
sin∠BAC= = ,
考点
2
平面图形中的计算问题
[例4] 在△ABC中,角A,B,C的对边分别为a,b,c.已知a=3,c=,B=45°.
(1)求sin C的值;
(2)在边BC上取一点D,使得cos∠ADC=-,求tan∠DAC的值.
[例4] 在△ABC中,角A,B,C的对边分别为a,b,c.已知a=3,c=,B=45°.
(1)求sin C的值;
在△ABC中,因为a=3,c=,B=45°,
由余弦定理b2=a2+c2-2accos B,
得b2=9 +2-2×3× cos 45°=5,
所以b= .
在△ABC中,由正弦定理,得,
所以sin C= .
[例4] 在△ABC中,角A,B,C的对边分别为a,b,c.已知a=3,c=,B=45°.
(2)在边BC上取一点D,使得cos∠ADC=-,求tan∠DAC的值.
在△ADC中,因为cos∠ADC=-,所以∠ADC为钝角,
而∠ADC+C+∠CAD= 180°,所以C为锐角.
故cos C= = ,则tan C= = .
因为cos ∠ADC=-,所以sin ∠ADC= = ,
tan ∠ADC= =-,
从而tan ∠DAC=tan(180°-∠ADC-C)=-tan(∠ADC+C)
=- =- = .
方法总结
具体解题思路如下:
(1)把所提供的平面图形拆分成若干个三角形,然后在各个三角形内利用正弦、余弦定理求解;
(2)寻找各个三角形之间的联系,交叉使用公共条件,求出结果.
求解平面图形中的计算问题,关键是梳理条件和所求问题的类型,然后将数据化归到三角形中,利用正弦定理或余弦定理建立已知和所求的关系.
与平面图形有关的解三角形问题的关键及思路
跟踪训练
如图,在平面四边形ABCD中,∠ACB与∠D互补,cos∠ACB= ,AC=BC=2,AB=4AD.
(1)求AB的长;
(2)求sin∠ACD.
所以AB=4.
如图,在平面四边形ABCD中,∠ACB与∠D互补,cos∠ACB= ,AC=BC=2,AB=4AD.
(1)求AB的长;
由余弦定理AB2=BC2+AC2-2AC·BCcos∠ACB,
得AB2=(2)2+(2)2-2×2×2×=16,
如图,在平面四边形ABCD中,∠ACB与∠D互补,cos∠ACB= ,AC=BC=2,AB=4AD.
(2)求sin∠ACD.
因为AB=4且AB=4AD,所以AD=1,
因为∠ACB与∠D互补,所以cos D=-cos∠ACB=-,
所以sin D= = ,
由正弦定理,得sin∠ACD= .
考点
3
正、余弦定理与其他知识的交汇
[例5] 已知△ABC的内角A,B,C的对边分别为a,b,c,________,若b=,________.
请从下面的三个条件中任选一个,两个结论中任选一个,组成一个完整的问题,并给出解答.
条件:①asin=bsin A,
②bsin A=acos,
③a2+c2-b2=abcos A+a2cos B.
结论:①求△ABC周长的取值范围;
②求△ABC面积的最大值.
则由正弦定理得sin Asin =sin Bsin A,
因为sin A≠0,所以sin =sin B.
由A+B+C=π,可得sin =cos . 故cos =2sin cos .
在△ABC中,由正弦定理,可得bsin A=asin B,
又bsin A=acos,
所以asin B=acos,即sin B=cos .
所以sin B= cos B+ sin B,可得tan B= .
选择条件①
因为cos ≠0,故sin = .
又因为B∈(0,π),所以B= .
选择条件②
又B∈(0,π),所以B= .
因为a2+c2-b2=abcos A+a2cos B,
所以由余弦定理,得2accos B=abcos A+a2cos B,
又a≠0,所以2ccos B=bcos A+acos B.
由正弦定理得2sin Ccos B=sin Bcos A+sin Acos B=sin(A+B)=sin C.
选择条件③
又C∈(0,π),所以sin C>0,所以cos B= .
因为B∈(0,π),所以B=.
解得a+c≤2(当且仅当a=c=时,等号成立).
又a+c>b=,所以2
因为b=.
所以由余弦定理得13=a2+c2-2accos B=a2+c2-ac=(a+c)2-3ac,
所以(a+c)2=13+3ac≤13+3 ,
故△ABC的周长的取值范围为(2,3 ].
因为b=,
所以由余弦定理结合基本不等式得13=a2+c2-2accos B=a2+c2-ac≥2ac-ac=ac(当且仅当a=c=时,等号成立).
所以△ABC的面积S= acsin B≤ × = ,
即△ABC的面积的最大值为.
选择结论②
方法总结
解答本题的关键是注意到三角形面积公式S△ABC= acsin B中的ac,与余弦定理中的a2+c2存在不等关系a2+c2≥2ac,利用余弦定理沟通二者,求出ac的最值即可.
关键点拨
跟踪训练
在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且.
(1)求角C的大小;
(2)若b=1,求c的取值范围.
在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且.
(1)求角C的大小;
因为,
所以b=ccos A+asin C,
由正弦定理得,sin B=sin Ccos A+sin Asin C,
又sin B=sin(A+C)=sin Acos C+cos Asin C.
所以sin Asin C=sin Acos C,
又0
(2)若b=1,求c的取值范围.
由(1)可知,A+B= ,又△ABC是锐角三角形,
所以 得
随堂检测
1.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD. 已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
A.50 米 B.50 米 C.50米 D.50米
设该扇形的半径为r米,连接CO.
由题意,得CD=150(米),OD=100(米),∠CDO=60°,
在△CDO中,CD2+OD2-2CD·OD·cos 60°=OC2,
即1502+1002-2×150×100×=r2,
解得r=50 .
B
所以AB=1+tan 30°·CB=1+20(米).
2.某工厂实施煤改电工程防治雾霾,欲拆除高为AB的烟囱,测绘人员取与烟囱底部B在同一水平面内的两个观测点C,D,测得∠BCD=75°,∠BDC=60°,CD=40米,并在点C处的正上方E处观测顶部A的仰角为30°,且CE=1米,则烟囱高AB=________米.
∠CBD=180°-∠BCD-∠BDC=45°,
在△CBD中,由正弦定理得BC= =20(米),
1+20
所以此船的航行速度v= = (海里/时).
3.一船自西向东匀速航行,上午10时到达灯塔P的南偏西75°,距灯塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则此船航行的速度为________海里/时.
如图,由题意知∠MPN=75°+45°=120°,∠PNM=45°.
在△PMN中,由正弦定理得,
所以MN=68× =34(海里).
又由M到N所用的时间为14-10=4(小时),
4.在△ABC中,内角A,B,C所对的边分别为a,b,c,若sin Asin Bcos C=sin2C,则=________,sin C的最大值为________.
又cos2C+sin2C=1,所以sin2C=1-cos2C≤ ,sin C≤ .
由题意结合正弦定理知abcos C=c2,即cos C=,
又cos C=,所以a2+b2-c2=2c2,得a2+b2=3c2,即=3.
故cos C== =≥ =,
当且仅当a=b时取等号,
3
因为(2a-c)cos B-bcos C=0,
所以2acos B-ccos B-bcos C=0,
由正弦定理得2sin Acos B-sin Ccos B-cos Csin B=0,
即2sin Acos B-sin(C+B)=0,
又C+B=π-A,所以sin(C+B)=sin A.
所以sin A(2cos B-1)=0.
在△ABC中,sin A≠0,
所以cos B= ,又B∈(0,π),所以B= .
5.在△ABC中,a,b,c分别是角A,B,C的对边,(2a-c)·cos B-bcos C=0.
(1)求角B的大小;
5.在△ABC中,a,b,c分别是角A,B,C的对边,(2a-c)·cos B-bcos C=0.
(2)设函数f(x)=2sin xcos xcos B- cos 2x,求函数f(x)的最大值及当f(x)取得最大值时x的值.
即当x=kπ+ (k∈Z)时,f(x)取得最大值1.
因为B= ,所以f(x)= sin 2x- cos 2x=sin ,
令2x- =2kπ+ (k∈Z),得x=kπ+(k∈Z),
本课小结
测量距离问题,测量高度问题,测量角度问题,是高考考查的热点,题型各种类型都有,难度中等.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
