人教版(2019)数学必修第二册8_5_2 直线与平面平行(1) 课件(共25张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册8_5_2 直线与平面平行(1) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 11:03:13 | ||
图片预览






文档简介
(共25张PPT)
8.5.2 直线与平面平行(1)
高一
必修二
本节目标
1.借助长方体,通过直观感知、了解空间中直线与平面平行的关系及判定定理.
2.理解直线与平面平行的判定定理,能用图形语言和符号语言表述定理,并能加以证明.
预习课本P135~137,思考并完成以下问题
直线与平面平行的判定定理是什么?
(2) 你有哪些方法可以判定直线与平面平行
课前预习
α
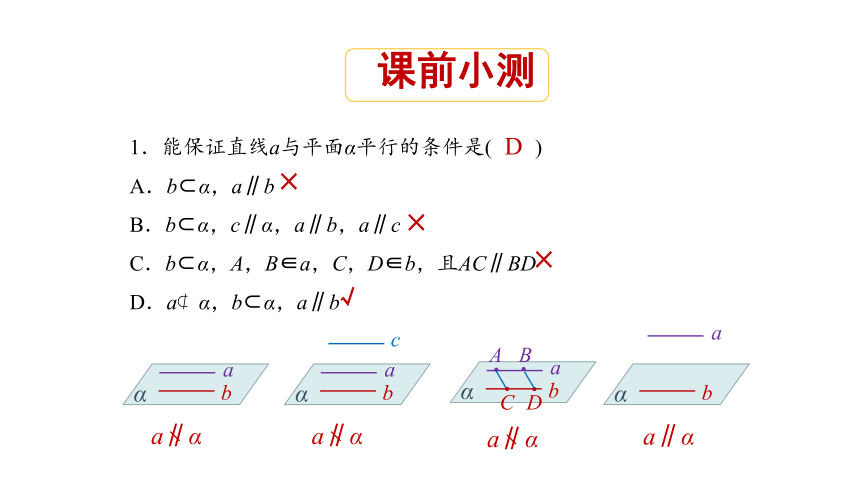
1.能保证直线a与平面α平行的条件是( )
A.b α,a∥b
B.b α,c∥α,a∥b,a∥c
C.b α,A,B∈a,C,D∈b,且AC∥BD
D.a α,b α,a∥b
课前小测
b
a
×
α
b
a
c
×
a∥α
a∥α
α
b
a
A
B
C
D
a∥α
×
α
b
a
a∥α
√
D
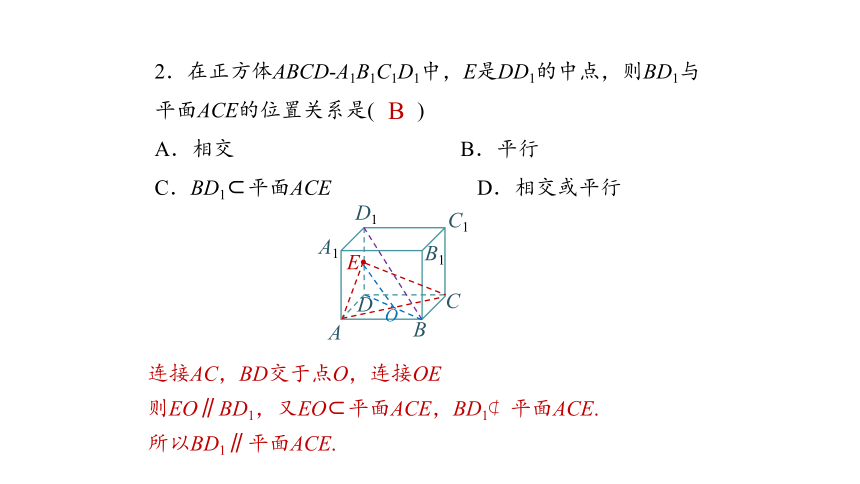
2.在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系是( )
A.相交 B.平行
C.BD1 平面ACE D.相交或平行
A
B
C
D
A1
B1
C1
D1
E
所以BD1∥平面ACE.
连接AC,BD交于点O,连接OE
O
则EO∥BD1,又EO 平面ACE,BD1 平面ACE.
B
新知探究
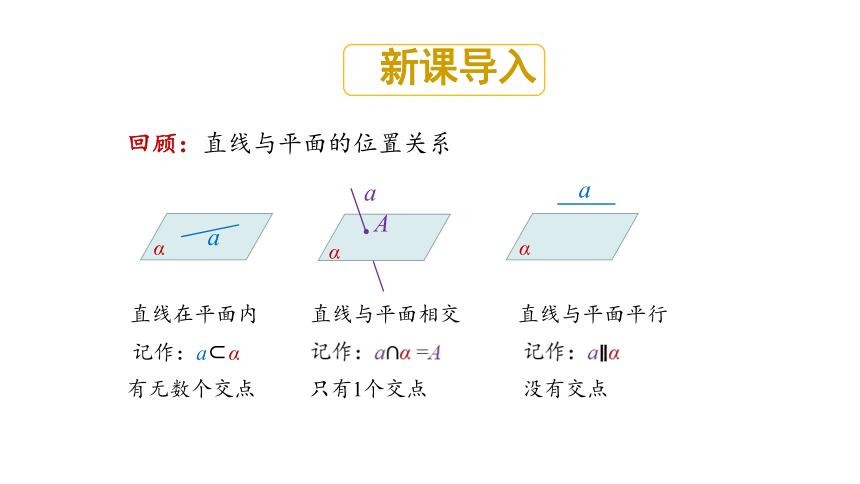
回顾:直线与平面的位置关系
α
a
直线在平面内
α
a
A
直线与平面相交
α
a
直线与平面平行
记作:a α
记作:aα =A
记作:aα
有无数个交点
只有1个交点
没有交点
新课导入
思考:怎样判定直线与平面平行呢?除了定义,还有没有其他方法?
新课导入
思考
?
如图,门扇的两边是平行的,当门扇绕着一边转动时,另一边与墙面有公共点吗?此时门扇转动的一边与墙面平行吗?
可以发现,无论门扇转动到什么位置,因为转动的一边与固定的一边总是平行的,所以它与墙面是平行的.
此定理将证明线面平行的问题转化为证明线线平行.
此定理可简记为:线线平行 线面平行.
直线与平面平行的判定(证明)
1.定义法
判定(证明)直线与平面无公共点.
2.判定定理
如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
用符号表示:a α,b α且a∥b a∥α.
3.体现了转化思想
题型突破
典例深度剖析 重点多维探究
题型一 线面平行判定定理的理解
[例1] 如果两直线a∥b,且a∥α,则b与α的位置关系是( )
A.相交 B.b∥α
C.b α D.b∥α或b α
D
α
b
a
α
b
a
b∥α
b α
总结提升
(1)直线a在平面α外,即a α;
(2)直线b在平面α内,即b α;
(3)两直线a,b平行,即a∥b;
线面平行的判定定理必须具备三个条件
这三个条件缺一不可.
跟踪训练
1. 下列说法正确的是( )
A.若直线l平行于平面α内的无数条直线,则l∥α
B.若直线a在平面α外,则a∥α
C.若直线a∩b= ,直线b α,则a∥α
D.若直线a∥b,b α,那么直线a就平行于平面α内的无数条直线
直线l还可以在平面α内
×
直线a在平面α外,包括平行和相交
×
a还可以与平面α相交或在平面α内
×
√
D
题型二 直线与平面平行的判定
[例2] 如图,在正方体ABCD- A1B1C1D1中,E,F,G分别是BC,CC1,BB1的中点,求证:EF∥平面AD1G.
则由E,F分别是BC,CC1的中点,知EF∥BC1.
又AB∥A1B1∥D1C1,且AB=A1B1=D1C1,
所以四边形ABC1D1是平行四边形,
所以BC1∥AD1,所以EF∥AD1.
又EF 平面AD1G,AD1 平面AD1G,
所以EF∥平面AD1G.
[证明] 连接BC1
总结提升
应用判定定理证明线面平行的步骤
找
证
结论
在平面内找到或作出一条与已知直线平行的直线
证明已知直线平行于找到(作出)的直线
由判定定理得出结论
上面的第一步“找”是证题的关键,其常用方法有:
①空间直线平行关系的传递性法;
②三角形中位线法;
③平行四边形法;
④线段成比例法.
易错提醒
线面平行判定定理应用的误区
(1)条件罗列不全,最易忘记的条件是“直线在平面外”.
(2)不能利用题目条件顺利地找到两平行直线.
跟踪训练
2. 在四面体ABCD中,M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是____________________.
平面ABD、平面ABC
如图所示,取CD的中点E.
则EM∶MA=1∶2,EN∶BN=1∶2,
所以MN∥AB.
又MN 平面ABD,MN 平面ABC,
AB 平面ABD,AB 平面ABC,
所以MN∥平面ABD,MN∥平面ABC.
3. 如图,四边形ABCD是平行四边形,P是平面ABCD外一点,M,N分别是AB,PC的中点.
求证:MN∥平面PAD.
证明:如图,取PD的中点G,连接GA,GN.
∵G,N分别是△PDC的边PD,PC的中点,
∴GN∥DC,GN= DC.
∵M为平行四边形ABCD的边AB的中点,
∴AM= DC,AM∥DC,∴AM∥GN,AM=GN,
∴四边形AMNG为平行四边形,∴MN∥AG.
又∵MN 平面PAD,AG 平面PAD,
∴MN∥平面PAD.
G
随堂检测
1.在正方体ABCD-A1B1C1D1中,M是棱CD上的动点,则直线MC1与平面AA1B1B的位置关系是( )
A.相交 B.平行
C.异面 D.相交或平行
A
B
C
D
A1
B1
C1
D1
M
B
2.如图,下列正三棱柱ABC-A1B1C1中,若M,N,P分别为其所在棱的中点,则不能得出AB∥平面MNP的是( )
在图A,B中,易知AB∥A1B1∥MN,所以AB∥平面MNP;
在图D中,易知AB∥PN,所以AB∥平面MNP;
在图C中,AB与平面MNP相交.
C
3. 如图,在下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是 .
①④
①中,取NP的中点O,连接MO,则MO∥AB,∴AB∥平面MNP;
②中,在平面MNP内找不到与AB平行的直线,故②不能得出;
③中,AB与平面MNP相交;
④中,∵AB∥NP,∴AB∥平面MNP.
O
本课小结
(1)利用判定定理判断或证明直线与平面平行的关键是在已知平面α内找一条直线b和已知直线a平行.即要证直线a与平面α平行,先证直线a与直线b平行.即由立体向平面转化.
证明线面平行的方法、步骤
(2)证明线面平行的一般步骤:
①在平面内找一条直线;
②证明线线平行;
③由判定定理得出结论.
(3)在与中点有关的平行问题中,常考虑中位线定理.
通过本节课,你学会了什么?
8.5.2 直线与平面平行(1)
高一
必修二
本节目标
1.借助长方体,通过直观感知、了解空间中直线与平面平行的关系及判定定理.
2.理解直线与平面平行的判定定理,能用图形语言和符号语言表述定理,并能加以证明.
预习课本P135~137,思考并完成以下问题
直线与平面平行的判定定理是什么?
(2) 你有哪些方法可以判定直线与平面平行
课前预习
α
1.能保证直线a与平面α平行的条件是( )
A.b α,a∥b
B.b α,c∥α,a∥b,a∥c
C.b α,A,B∈a,C,D∈b,且AC∥BD
D.a α,b α,a∥b
课前小测
b
a
×
α
b
a
c
×
a∥α
a∥α
α
b
a
A
B
C
D
a∥α
×
α
b
a
a∥α
√
D
2.在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系是( )
A.相交 B.平行
C.BD1 平面ACE D.相交或平行
A
B
C
D
A1
B1
C1
D1
E
所以BD1∥平面ACE.
连接AC,BD交于点O,连接OE
O
则EO∥BD1,又EO 平面ACE,BD1 平面ACE.
B
新知探究
回顾:直线与平面的位置关系
α
a
直线在平面内
α
a
A
直线与平面相交
α
a
直线与平面平行
记作:a α
记作:aα =A
记作:aα
有无数个交点
只有1个交点
没有交点
新课导入
思考:怎样判定直线与平面平行呢?除了定义,还有没有其他方法?
新课导入
思考
?
如图,门扇的两边是平行的,当门扇绕着一边转动时,另一边与墙面有公共点吗?此时门扇转动的一边与墙面平行吗?
可以发现,无论门扇转动到什么位置,因为转动的一边与固定的一边总是平行的,所以它与墙面是平行的.
此定理将证明线面平行的问题转化为证明线线平行.
此定理可简记为:线线平行 线面平行.
直线与平面平行的判定(证明)
1.定义法
判定(证明)直线与平面无公共点.
2.判定定理
如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
用符号表示:a α,b α且a∥b a∥α.
3.体现了转化思想
题型突破
典例深度剖析 重点多维探究
题型一 线面平行判定定理的理解
[例1] 如果两直线a∥b,且a∥α,则b与α的位置关系是( )
A.相交 B.b∥α
C.b α D.b∥α或b α
D
α
b
a
α
b
a
b∥α
b α
总结提升
(1)直线a在平面α外,即a α;
(2)直线b在平面α内,即b α;
(3)两直线a,b平行,即a∥b;
线面平行的判定定理必须具备三个条件
这三个条件缺一不可.
跟踪训练
1. 下列说法正确的是( )
A.若直线l平行于平面α内的无数条直线,则l∥α
B.若直线a在平面α外,则a∥α
C.若直线a∩b= ,直线b α,则a∥α
D.若直线a∥b,b α,那么直线a就平行于平面α内的无数条直线
直线l还可以在平面α内
×
直线a在平面α外,包括平行和相交
×
a还可以与平面α相交或在平面α内
×
√
D
题型二 直线与平面平行的判定
[例2] 如图,在正方体ABCD- A1B1C1D1中,E,F,G分别是BC,CC1,BB1的中点,求证:EF∥平面AD1G.
则由E,F分别是BC,CC1的中点,知EF∥BC1.
又AB∥A1B1∥D1C1,且AB=A1B1=D1C1,
所以四边形ABC1D1是平行四边形,
所以BC1∥AD1,所以EF∥AD1.
又EF 平面AD1G,AD1 平面AD1G,
所以EF∥平面AD1G.
[证明] 连接BC1
总结提升
应用判定定理证明线面平行的步骤
找
证
结论
在平面内找到或作出一条与已知直线平行的直线
证明已知直线平行于找到(作出)的直线
由判定定理得出结论
上面的第一步“找”是证题的关键,其常用方法有:
①空间直线平行关系的传递性法;
②三角形中位线法;
③平行四边形法;
④线段成比例法.
易错提醒
线面平行判定定理应用的误区
(1)条件罗列不全,最易忘记的条件是“直线在平面外”.
(2)不能利用题目条件顺利地找到两平行直线.
跟踪训练
2. 在四面体ABCD中,M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是____________________.
平面ABD、平面ABC
如图所示,取CD的中点E.
则EM∶MA=1∶2,EN∶BN=1∶2,
所以MN∥AB.
又MN 平面ABD,MN 平面ABC,
AB 平面ABD,AB 平面ABC,
所以MN∥平面ABD,MN∥平面ABC.
3. 如图,四边形ABCD是平行四边形,P是平面ABCD外一点,M,N分别是AB,PC的中点.
求证:MN∥平面PAD.
证明:如图,取PD的中点G,连接GA,GN.
∵G,N分别是△PDC的边PD,PC的中点,
∴GN∥DC,GN= DC.
∵M为平行四边形ABCD的边AB的中点,
∴AM= DC,AM∥DC,∴AM∥GN,AM=GN,
∴四边形AMNG为平行四边形,∴MN∥AG.
又∵MN 平面PAD,AG 平面PAD,
∴MN∥平面PAD.
G
随堂检测
1.在正方体ABCD-A1B1C1D1中,M是棱CD上的动点,则直线MC1与平面AA1B1B的位置关系是( )
A.相交 B.平行
C.异面 D.相交或平行
A
B
C
D
A1
B1
C1
D1
M
B
2.如图,下列正三棱柱ABC-A1B1C1中,若M,N,P分别为其所在棱的中点,则不能得出AB∥平面MNP的是( )
在图A,B中,易知AB∥A1B1∥MN,所以AB∥平面MNP;
在图D中,易知AB∥PN,所以AB∥平面MNP;
在图C中,AB与平面MNP相交.
C
3. 如图,在下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是 .
①④
①中,取NP的中点O,连接MO,则MO∥AB,∴AB∥平面MNP;
②中,在平面MNP内找不到与AB平行的直线,故②不能得出;
③中,AB与平面MNP相交;
④中,∵AB∥NP,∴AB∥平面MNP.
O
本课小结
(1)利用判定定理判断或证明直线与平面平行的关键是在已知平面α内找一条直线b和已知直线a平行.即要证直线a与平面α平行,先证直线a与直线b平行.即由立体向平面转化.
证明线面平行的方法、步骤
(2)证明线面平行的一般步骤:
①在平面内找一条直线;
②证明线线平行;
③由判定定理得出结论.
(3)在与中点有关的平行问题中,常考虑中位线定理.
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
