人教版(2019)数学必修第二册8_6_3平面与平面垂直(1) 课件(共43张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册8_6_3平面与平面垂直(1) 课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 11:04:05 | ||
图片预览








文档简介
(共43张PPT)
8.6.3 平面与平面垂直(1)
高一
必修二
本节目标
1.理解二面角的有关概念,会作二面角的平面角,能求简单二面角平面角的大小.
2.了解面面垂直的定义,掌握面面垂直的判定定理,初步学会用定理证明垂直关系.
课前预习
预习课本P155~158,思考并完成以下问题
1.什么叫做二面角?什么叫做二面角的平面角?
2.两个平面互相垂直是怎样定义的?两个平面互相垂直的判定定理是什么?
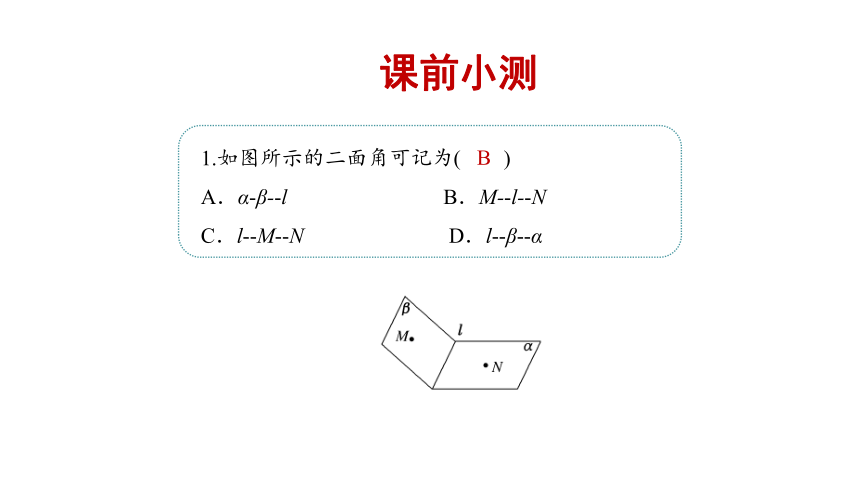
课前小测
1.如图所示的二面角可记为( )
A.α-β- l B.M- l- N
C.l -M -N D.l -β -α
B
2.直线l⊥平面α,l 平面β,则α与β的位置关系是( )
A.平行 B.可能重合
C.相交且垂直 D.相交不垂直
直线l⊥平面α
l 平面β
平面β ⊥平面α
C
3.已知直线l⊥平面α,则经过l且和α垂直的平面( )
A.有一个 B.有两个
C.有无数个 D.不存在
直线l⊥平面α
经过l的任一平面都和α垂直
C
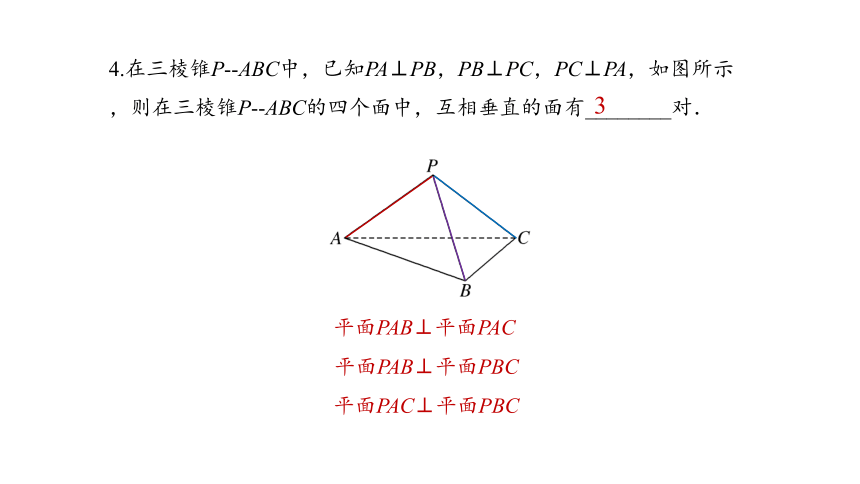
4.在三棱锥P -ABC中,已知PA⊥PB,PB⊥PC,PC⊥PA,如图所示,则在三棱锥P -ABC的四个面中,互相垂直的面有________对.
平面PAC⊥平面PBC
平面PAB⊥平面PAC
平面PAB⊥平面PBC
3
5.在正方体ABCD-A1B1C1D1中,二面角A-BC-A1的平面角等于______.
AB⊥BC
A1B⊥BC
∠ABA1 即为二面角A BC A1的平面角
AB=AA1,且AB⊥AA1
∠ABA1=45°
45°
新课导入
回顾:
空间几何中,异面直线所成角是怎样定义的?
已知两条异面直线a,b,经过空间任一点O分别作直线a′∥a,b′∥b,我们把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角).
范围:
α
a
b
O
a′
b′
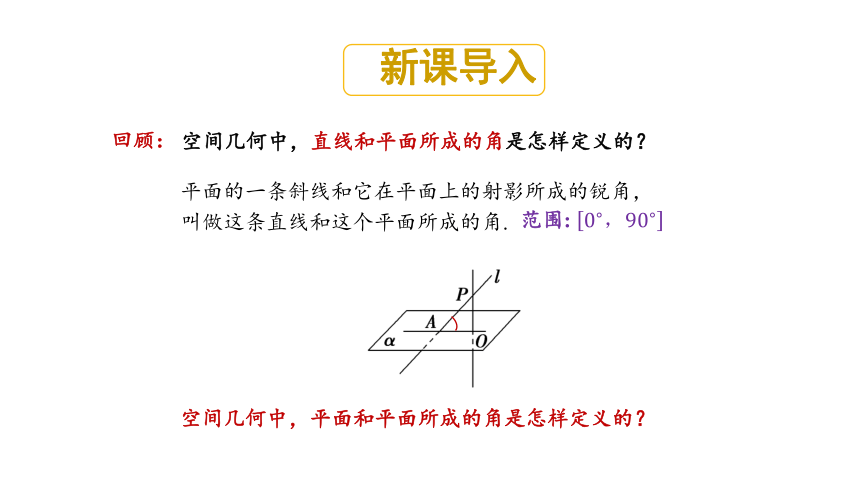
新课导入
回顾:
空间几何中,直线和平面所成的角是怎样定义的?
平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.
范围:
空间几何中,平面和平面所成的角是怎样定义的?
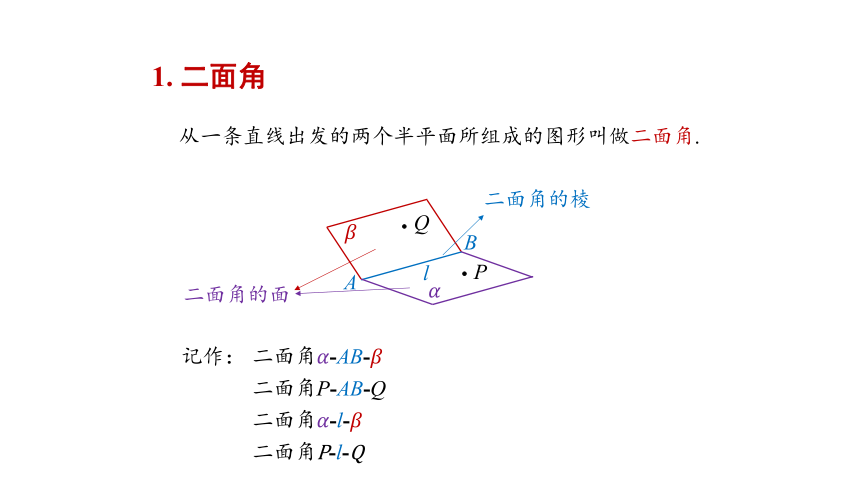
新知探究
1. 二面角
A
B
l
Q
P
从一条直线出发的两个半平面所组成的图形叫做二面角.
二面角的棱
二面角的面
记作:
二面角-AB-
二面角-l-
二面角P-AB-Q
二面角-l-
如图,在日常生活中,我们常说“把门开大一些”,是指哪个角大一些?受此启发,你认为应该怎样刻画二面角的大小呢?
思考
?
l
B
A
O
如图,在二面角-l-的棱l上任取一点O,以点O为垂足,在半平面和内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.
思考:
∠AOB的大小与点O在l上的位置有关吗?为什么?
2. 二面角的平面角
l
B
A
O
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.
平面角是直角的二面角叫做直二面角.
二面角的平面角的取值范围是.
3. 直二面角
观察
教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数.
教室的墙面所在的平面与地面所在平面相交,它们所成的二面角是直二面角.
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
平面与垂直,记作⊥
画法:
画两个垂直的平面时,通常把表示平面的两个平行四边形的一组边画成垂直. 如图所示.
4. 两个平面互相垂直
观察
建筑工人在砌墙时,常用铅垂线来检测所砌的墙面与地面是否垂直.如果系有铅锤的细线紧贴墙面,工人师傅就认为墙面垂直于地面,否则他就认为墙面不垂直于地面.这种方法说明了什么道理?
墙面经过地面的垂线,那么墙面与地面垂直.
5. 两个平面互相垂直的判定定理
定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直.
符号语言:
a
a
图形语言:
简记:线面垂直,则面面垂直
线线垂直
线面垂直
面面垂直
知识拓展
1.二面角与平面几何中的角的对比
平面几何中的角 二面角
图形
定义 从平面内一点出发的两条射线组成的图形 从一条直线出发的两个半平面组成的图形
表示法 由射线—点(顶点)—射线构成,即为∠AOB 由半平面—线(棱)—半平面构成,记为二面角α-l-β
意义 定量的反映两条直线的位置关系 定量的反映两个平面的位置关系
知识拓展
2.剖析平面与平面垂直
(1)两个平面垂直是两个平面相交的特殊情况.例如正方体中任意相邻两个面都是互相垂直的.
(2)两个平面垂直和两条直线互相垂直的共同点:都是通过所成的角是直角定义的.
3.详解平面与平面垂直的判定定理
(1)本质:通过直线与平面垂直来证明平面与平面垂直,即线面垂直 面面垂直.
(2)证题思路:处理面面垂直问题转化为处理线面垂直问题,进一步转化为处理线线垂直问题来解决.
题型突破
典例深度剖析 重点多维探究
题型一 对线面垂直定义及判断定理的理解
[例1] 如图,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
(1)求二面角A-PD-C平面角的度数;
(2)求二面角B-PA-C平面角的度数.
[例1] 如图,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
(1)求二面角A-PD-C平面角的度数;
∵PA⊥平面ABCD,
∴PA⊥CD.
又四边形ABCD为正方形,
∴CD⊥AD. PA∩AD=A,
∴CD⊥平面PAD. 又CD 平面PCD,
∴平面PAD⊥平面PCD.
∴二面角A-PD-C平面角的度数为90°.
[例1] 如图,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
(2)求二面角B-PA-C平面角的度数.
∵PA⊥平面ABCD,
∴AB⊥PA,AC⊥PA.
∴∠BAC为二面角B-PA-C的平面角.
又四边形ABCD为正方形,
∴∠BAC=45°.
即二面角B-PA-C平面角的度数为45°.
总结提升
(1)清楚二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点.
(2)求二面角的大小的方法
一作:即先作出二面角的平面角;
二证:即说明所作角是二面角的平面角;
三求:即利用二面角的平面角所在的三角形算出角的三角函数值,其中关键是“作”.
解决二面角问题的策略
由已知PA⊥平面ABC,BC 平面ABC, ∴PA⊥BC.
∵AB是⊙O的直径,且点C在圆周上, ∴AC⊥BC.
又∵PA∩AC=A,PA,AC 平面PAC, ∴BC⊥平面PAC.
又PC 平面PAC,∴PC⊥BC.
又∵BC是二面角P-BC-A的棱,
∴∠PCA是二面角P-BC-A的平面角.
由PA=AC知△PAC是等腰直角三角形,
∴∠PCA=45°,即二面角P-BC-A的大小是45°.
跟踪训练
1. 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小.
题型二 面面垂直的判定
[例2] 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
[证明] 法一:(利用定义证明)
因为∠BSA=∠CSA=60°,SA=SB=SC,
所以△ASB和△ASC是等边三角形,
则有SA=SB=SC=AB=AC,令其值为a,
则△ABC和△SBC为共底边BC的等腰三角形.
取BC的中点D,如图所示,
D
连接AD,SD,则AD⊥BC,SD⊥BC,
题型二 面面垂直的判定
[例2] 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
D
所以∠ADS为二面角A-BC-S的平面角.
在Rt△BSC中,因为SB=SC=a,
所以SD= a,BD= = a.
在Rt△ABD中,AD= a,
在△ADS中,因为SD2+AD2=SA2,
所以∠ADS=90°,即二面角A-BC-S为直二面角,
故平面ABC⊥平面SBC.
题型二 面面垂直的判定
[例2] 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
D
连接AD,SD,则AD⊥BC,SD⊥BC,
所以∠ADS为二面角A-BC-S的平面角.
在Rt△BSC中,因为SB=SC=a,
所以SD= a,BD= = a.
在Rt△ABD中,AD= a,
在△ADS中,因为SD2+AD2=SA2,
所以∠ADS=90°,即二面角A-BC-S为直二面角,
故平面ABC⊥平面SBC.
题型二 面面垂直的判定
[例2] 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
D
法二:(利用判定定理)
因为SA=SB=SC,且∠BSA=∠CSA=60°,
所以SA=AB=AC,
所以点A在平面SBC上的射影为△SBC的外心.
因为△SBC为直角三角形,
所以点A在△SBC上的射影D为斜边BC的中点,
所以AD⊥平面SBC.
又因为AD 平面ABC,所以平面ABC⊥平面SBC.
总结提升
(1)定义法:即说明两个半平面所成的二面角是直二面角;
(2)判定定理法:在其中一个平面内寻找一条直线与另一个平面垂直,即把问题转化为“线面垂直”;
(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
证明面面垂直常用的方法
多维探究
1.[变条件,变结论]本例中,若SA=SB=SC=2,其他条件不变,如何求三棱锥S-ABC的体积呢?
由例2法一或法二可得SD⊥AD.
又因为SD⊥BC,AD∩BC=D,
所以SD⊥平面ABC,
即SD的长就是顶点S到底面ABC的距离.
因为S△ABC= ×BC×AD= ×2×=2,SD=,
所以VS-ABC= ×S△ABC×SD= .
D
2. [变条件,变结论]本例变为:如图,在四面体ABCD中,BD=a,AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD.
证明:取BD的中点E,连接AE,CE,
因为△ABD与△BCD是全等的等腰三角形,
所以AE⊥BD,CE⊥BD,
即∠AEC为二面角A-BD-C的平面角,
在△ABD中,AB=a,BE= BD= a,
所以AE= = a,同理,CE= a.
E
2. [变条件,变结论]本例变为:如图,在四面体ABCD中,BD=a,AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD.
E
在△AEC中,AE=CE= a,AC=a,
故AC2=AE2+CE2,
所以AE⊥CE,
即∠AEC=90°,
所以二面角A BD C的平面角为90°,
所以平面ABD⊥平面BCD.
3.[变条件,变结论]将本例变为:在四面体ABCD中,CB=CD,AD⊥BD,且E,F分别是AB,BD的中点.
求证:(1)直线EF∥平面ACD;
证明:因为E,F分别是AB,BD 的中点,
所以EF是△ABD的中位线,
所以EF∥AD,
因为EF 平面ACD,AD 平面ACD,
所以直线EF∥平面ACD.
3.[变条件,变结论]将本例变为:在四面体ABCD中,CB=CD,AD⊥BD,且E,F分别是AB,BD的中点.
求证: (2)平面EFC⊥平面BCD.
因为AD⊥BD,EF∥AD,
所以EF⊥BD.
因为CB=CD,F是BD的中点,
所以CF⊥BD.
又EF∩CF=F,所以BD⊥平面EFC.
因为BD 平面BCD,
所以平面EFC⊥平面BCD.
随堂检测
1.下列命题中正确的是( )
A.平面α和β分别过两条互相垂直的直线,则α⊥β
B.若平面α内的一条直线垂直于平面β内的两条平行直线,则α⊥β
C.若平面α内的一条直线垂直于平面β内的两条相交直线,则α⊥β
D.若平面α内的一条直线垂直于平面β内的无数条直线,则α⊥β
当平面α和β分别过两条互相垂直且异面的直线时,平面α和β有可能平行
×
×
×
√
C
2.如图,在正方体ABCD-A1B1C1D1中,截面C1D1AB与底面ABCD所成二面角C1-AB-C的大小为________.
∵AB⊥BC,AB⊥BC1,
∴∠C1BC为二面角C1-AB-C的平面角,大小为45°.
45°
3.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.
求证:平面DD1E⊥平面CD1E.
证明:在矩形ABCD中,E为AB的中点,
AD=2,AB=4,所以DE=CE=2,
因为CD=4,所以CE⊥DE,
因为D1D⊥平面ABCD,所以D1D⊥CE,
因为D1D∩DE=D,所以CE⊥平面D1DE,
又CE 平面CED1,
所以平面DD1E⊥平面CD1E.
本课小结
一、平面与平面垂直的判定
1.定义:两个相交平面所成二面角为直二面角.
2.判定定理:在一个平面内找到另一个平面的垂线.
二、数学思想
线线垂直
线面垂直
面面垂直
通过本节课,你学会了什么?
8.6.3 平面与平面垂直(1)
高一
必修二
本节目标
1.理解二面角的有关概念,会作二面角的平面角,能求简单二面角平面角的大小.
2.了解面面垂直的定义,掌握面面垂直的判定定理,初步学会用定理证明垂直关系.
课前预习
预习课本P155~158,思考并完成以下问题
1.什么叫做二面角?什么叫做二面角的平面角?
2.两个平面互相垂直是怎样定义的?两个平面互相垂直的判定定理是什么?
课前小测
1.如图所示的二面角可记为( )
A.α-β- l B.M- l- N
C.l -M -N D.l -β -α
B
2.直线l⊥平面α,l 平面β,则α与β的位置关系是( )
A.平行 B.可能重合
C.相交且垂直 D.相交不垂直
直线l⊥平面α
l 平面β
平面β ⊥平面α
C
3.已知直线l⊥平面α,则经过l且和α垂直的平面( )
A.有一个 B.有两个
C.有无数个 D.不存在
直线l⊥平面α
经过l的任一平面都和α垂直
C
4.在三棱锥P -ABC中,已知PA⊥PB,PB⊥PC,PC⊥PA,如图所示,则在三棱锥P -ABC的四个面中,互相垂直的面有________对.
平面PAC⊥平面PBC
平面PAB⊥平面PAC
平面PAB⊥平面PBC
3
5.在正方体ABCD-A1B1C1D1中,二面角A-BC-A1的平面角等于______.
AB⊥BC
A1B⊥BC
∠ABA1 即为二面角A BC A1的平面角
AB=AA1,且AB⊥AA1
∠ABA1=45°
45°
新课导入
回顾:
空间几何中,异面直线所成角是怎样定义的?
已知两条异面直线a,b,经过空间任一点O分别作直线a′∥a,b′∥b,我们把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角).
范围:
α
a
b
O
a′
b′
新课导入
回顾:
空间几何中,直线和平面所成的角是怎样定义的?
平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.
范围:
空间几何中,平面和平面所成的角是怎样定义的?
新知探究
1. 二面角
A
B
l
Q
P
从一条直线出发的两个半平面所组成的图形叫做二面角.
二面角的棱
二面角的面
记作:
二面角-AB-
二面角-l-
二面角P-AB-Q
二面角-l-
如图,在日常生活中,我们常说“把门开大一些”,是指哪个角大一些?受此启发,你认为应该怎样刻画二面角的大小呢?
思考
?
l
B
A
O
如图,在二面角-l-的棱l上任取一点O,以点O为垂足,在半平面和内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.
思考:
∠AOB的大小与点O在l上的位置有关吗?为什么?
2. 二面角的平面角
l
B
A
O
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.
平面角是直角的二面角叫做直二面角.
二面角的平面角的取值范围是.
3. 直二面角
观察
教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数.
教室的墙面所在的平面与地面所在平面相交,它们所成的二面角是直二面角.
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
平面与垂直,记作⊥
画法:
画两个垂直的平面时,通常把表示平面的两个平行四边形的一组边画成垂直. 如图所示.
4. 两个平面互相垂直
观察
建筑工人在砌墙时,常用铅垂线来检测所砌的墙面与地面是否垂直.如果系有铅锤的细线紧贴墙面,工人师傅就认为墙面垂直于地面,否则他就认为墙面不垂直于地面.这种方法说明了什么道理?
墙面经过地面的垂线,那么墙面与地面垂直.
5. 两个平面互相垂直的判定定理
定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直.
符号语言:
a
a
图形语言:
简记:线面垂直,则面面垂直
线线垂直
线面垂直
面面垂直
知识拓展
1.二面角与平面几何中的角的对比
平面几何中的角 二面角
图形
定义 从平面内一点出发的两条射线组成的图形 从一条直线出发的两个半平面组成的图形
表示法 由射线—点(顶点)—射线构成,即为∠AOB 由半平面—线(棱)—半平面构成,记为二面角α-l-β
意义 定量的反映两条直线的位置关系 定量的反映两个平面的位置关系
知识拓展
2.剖析平面与平面垂直
(1)两个平面垂直是两个平面相交的特殊情况.例如正方体中任意相邻两个面都是互相垂直的.
(2)两个平面垂直和两条直线互相垂直的共同点:都是通过所成的角是直角定义的.
3.详解平面与平面垂直的判定定理
(1)本质:通过直线与平面垂直来证明平面与平面垂直,即线面垂直 面面垂直.
(2)证题思路:处理面面垂直问题转化为处理线面垂直问题,进一步转化为处理线线垂直问题来解决.
题型突破
典例深度剖析 重点多维探究
题型一 对线面垂直定义及判断定理的理解
[例1] 如图,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
(1)求二面角A-PD-C平面角的度数;
(2)求二面角B-PA-C平面角的度数.
[例1] 如图,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
(1)求二面角A-PD-C平面角的度数;
∵PA⊥平面ABCD,
∴PA⊥CD.
又四边形ABCD为正方形,
∴CD⊥AD. PA∩AD=A,
∴CD⊥平面PAD. 又CD 平面PCD,
∴平面PAD⊥平面PCD.
∴二面角A-PD-C平面角的度数为90°.
[例1] 如图,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
(2)求二面角B-PA-C平面角的度数.
∵PA⊥平面ABCD,
∴AB⊥PA,AC⊥PA.
∴∠BAC为二面角B-PA-C的平面角.
又四边形ABCD为正方形,
∴∠BAC=45°.
即二面角B-PA-C平面角的度数为45°.
总结提升
(1)清楚二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点.
(2)求二面角的大小的方法
一作:即先作出二面角的平面角;
二证:即说明所作角是二面角的平面角;
三求:即利用二面角的平面角所在的三角形算出角的三角函数值,其中关键是“作”.
解决二面角问题的策略
由已知PA⊥平面ABC,BC 平面ABC, ∴PA⊥BC.
∵AB是⊙O的直径,且点C在圆周上, ∴AC⊥BC.
又∵PA∩AC=A,PA,AC 平面PAC, ∴BC⊥平面PAC.
又PC 平面PAC,∴PC⊥BC.
又∵BC是二面角P-BC-A的棱,
∴∠PCA是二面角P-BC-A的平面角.
由PA=AC知△PAC是等腰直角三角形,
∴∠PCA=45°,即二面角P-BC-A的大小是45°.
跟踪训练
1. 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小.
题型二 面面垂直的判定
[例2] 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
[证明] 法一:(利用定义证明)
因为∠BSA=∠CSA=60°,SA=SB=SC,
所以△ASB和△ASC是等边三角形,
则有SA=SB=SC=AB=AC,令其值为a,
则△ABC和△SBC为共底边BC的等腰三角形.
取BC的中点D,如图所示,
D
连接AD,SD,则AD⊥BC,SD⊥BC,
题型二 面面垂直的判定
[例2] 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
D
所以∠ADS为二面角A-BC-S的平面角.
在Rt△BSC中,因为SB=SC=a,
所以SD= a,BD= = a.
在Rt△ABD中,AD= a,
在△ADS中,因为SD2+AD2=SA2,
所以∠ADS=90°,即二面角A-BC-S为直二面角,
故平面ABC⊥平面SBC.
题型二 面面垂直的判定
[例2] 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
D
连接AD,SD,则AD⊥BC,SD⊥BC,
所以∠ADS为二面角A-BC-S的平面角.
在Rt△BSC中,因为SB=SC=a,
所以SD= a,BD= = a.
在Rt△ABD中,AD= a,
在△ADS中,因为SD2+AD2=SA2,
所以∠ADS=90°,即二面角A-BC-S为直二面角,
故平面ABC⊥平面SBC.
题型二 面面垂直的判定
[例2] 如图所示,在四面体ABCS 中,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.
求证:平面ABC⊥平面SBC.
D
法二:(利用判定定理)
因为SA=SB=SC,且∠BSA=∠CSA=60°,
所以SA=AB=AC,
所以点A在平面SBC上的射影为△SBC的外心.
因为△SBC为直角三角形,
所以点A在△SBC上的射影D为斜边BC的中点,
所以AD⊥平面SBC.
又因为AD 平面ABC,所以平面ABC⊥平面SBC.
总结提升
(1)定义法:即说明两个半平面所成的二面角是直二面角;
(2)判定定理法:在其中一个平面内寻找一条直线与另一个平面垂直,即把问题转化为“线面垂直”;
(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
证明面面垂直常用的方法
多维探究
1.[变条件,变结论]本例中,若SA=SB=SC=2,其他条件不变,如何求三棱锥S-ABC的体积呢?
由例2法一或法二可得SD⊥AD.
又因为SD⊥BC,AD∩BC=D,
所以SD⊥平面ABC,
即SD的长就是顶点S到底面ABC的距离.
因为S△ABC= ×BC×AD= ×2×=2,SD=,
所以VS-ABC= ×S△ABC×SD= .
D
2. [变条件,变结论]本例变为:如图,在四面体ABCD中,BD=a,AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD.
证明:取BD的中点E,连接AE,CE,
因为△ABD与△BCD是全等的等腰三角形,
所以AE⊥BD,CE⊥BD,
即∠AEC为二面角A-BD-C的平面角,
在△ABD中,AB=a,BE= BD= a,
所以AE= = a,同理,CE= a.
E
2. [变条件,变结论]本例变为:如图,在四面体ABCD中,BD=a,AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD.
E
在△AEC中,AE=CE= a,AC=a,
故AC2=AE2+CE2,
所以AE⊥CE,
即∠AEC=90°,
所以二面角A BD C的平面角为90°,
所以平面ABD⊥平面BCD.
3.[变条件,变结论]将本例变为:在四面体ABCD中,CB=CD,AD⊥BD,且E,F分别是AB,BD的中点.
求证:(1)直线EF∥平面ACD;
证明:因为E,F分别是AB,BD 的中点,
所以EF是△ABD的中位线,
所以EF∥AD,
因为EF 平面ACD,AD 平面ACD,
所以直线EF∥平面ACD.
3.[变条件,变结论]将本例变为:在四面体ABCD中,CB=CD,AD⊥BD,且E,F分别是AB,BD的中点.
求证: (2)平面EFC⊥平面BCD.
因为AD⊥BD,EF∥AD,
所以EF⊥BD.
因为CB=CD,F是BD的中点,
所以CF⊥BD.
又EF∩CF=F,所以BD⊥平面EFC.
因为BD 平面BCD,
所以平面EFC⊥平面BCD.
随堂检测
1.下列命题中正确的是( )
A.平面α和β分别过两条互相垂直的直线,则α⊥β
B.若平面α内的一条直线垂直于平面β内的两条平行直线,则α⊥β
C.若平面α内的一条直线垂直于平面β内的两条相交直线,则α⊥β
D.若平面α内的一条直线垂直于平面β内的无数条直线,则α⊥β
当平面α和β分别过两条互相垂直且异面的直线时,平面α和β有可能平行
×
×
×
√
C
2.如图,在正方体ABCD-A1B1C1D1中,截面C1D1AB与底面ABCD所成二面角C1-AB-C的大小为________.
∵AB⊥BC,AB⊥BC1,
∴∠C1BC为二面角C1-AB-C的平面角,大小为45°.
45°
3.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.
求证:平面DD1E⊥平面CD1E.
证明:在矩形ABCD中,E为AB的中点,
AD=2,AB=4,所以DE=CE=2,
因为CD=4,所以CE⊥DE,
因为D1D⊥平面ABCD,所以D1D⊥CE,
因为D1D∩DE=D,所以CE⊥平面D1DE,
又CE 平面CED1,
所以平面DD1E⊥平面CD1E.
本课小结
一、平面与平面垂直的判定
1.定义:两个相交平面所成二面角为直二面角.
2.判定定理:在一个平面内找到另一个平面的垂线.
二、数学思想
线线垂直
线面垂直
面面垂直
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
