人教版(2019)数学必修第二册8_6_2直线与平面垂直(1) 课件(共48张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册8_6_2直线与平面垂直(1) 课件(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 11:04:37 | ||
图片预览











文档简介
(共48张PPT)
8.6.2 直线与平面垂直(1)
高一
必修二
本节目标
1.借助长方体,通过直观感知、了解空间中直线与平面垂直,理解直线与平面垂直的定义.
2.理解直线与平面垂直的判定定理,并会用其判断直线与平面垂直.
3.理解直线与平面所成角的概念,并能解决简单的线面角问题.
预习课本P149~152,思考并完成以下问题
3.直线与平面所成的角是怎样定义的?直线与平面所成的角的范围是什么?
课前预习
1.直线与平面垂直的定义是怎样的?
2.直线与平面垂直的判定定理是什么?
1.下列说法中,正确的个数是( )
课前小测
①若直线l与平面α内的一条直线垂直,则l⊥α;
②若直线l与平面α内的两条直线垂直,则l⊥α;
③若直线l与平面α内的两条相交直线垂直,则l⊥α;
④若直线l与平面α内的任意一条直线垂直,则l⊥α.
该直线与平面可能平行,也可能斜交,也可能在平面内
该直线与平面可能平行,也可能斜交,也可能在平面内
B
A.4 B.2 C.3 D.1
×
×
√
√
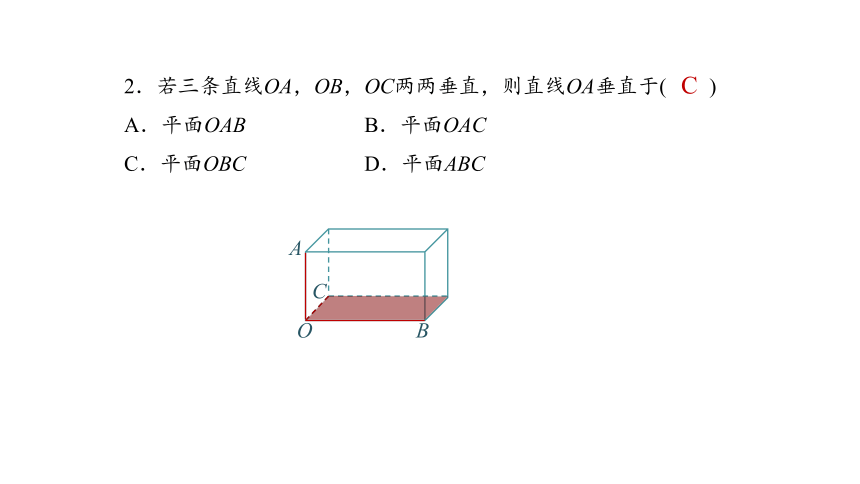
2.若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
A.平面OAB B.平面OAC
C.平面OBC D.平面ABC
O
B
C
A
C
3.一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( )
A.平行 B.垂直
C.相交不垂直 D.不确定
B
一条直线和三角形的两边同时垂直
这条直线垂直三角形所在平面
这条直线垂直第三边
4.在正方体ABCD- A1B1C1D1中,直线AB1与平面ABCD所成的角等于________.
如图,正方体ABCD- A1B1C1D1中,B1B⊥平面ABCD,
所以AB即为AB1在平面ABCD中的射影,
∠B1AB即为直线AB1与平面ABCD所成的角.
由题意知,∠B1AB=45°,故所求角为45°.
45°
新课导入
空间中直线与平面有几种位置关系?
α
a
α
a
A
α
a
a
a∥
a=A
生活中有很多直线与平面垂直的实例
新知探究
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
请给直线与平面垂直下定义.
A
B
直线垂直于平面内任意一条直线.
任意一条
1.直线与平面垂直
定义 如果直线l与平面α内的___________直线都垂直,我们就说直线l与平面α互相垂直
记法 l⊥α
有关概念 直线l叫做平面α的______,平面α叫做直线l的_______.它们唯一的公共点P叫做________.
图示
画法 画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
任意一条
垂线
垂面
垂足
线面垂直的定义常这样使用
α
l
a
l⊥α
a
l⊥a
简记:若线面垂直,则线线垂直
思考
?
在同一平面内,过一点有且只有一条直线与已知直线垂直,将这一结论推广到空间,过一点垂直于已知平面的直线有几条?为什么?
过一点垂直于已知平面的直线有且只有一条.
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
探究
如图,准备一块三角形的硬纸片,做一个试验:
A
B
C
D
过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触).
问题:(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在平面垂直?
A
B
C
D
α
A
C
D
B
当且仅当折痕AD是BC边上的高时,AD所在直线与桌面所在平面α垂直.
2. 直线与平面垂直的判定定理
文字语言 如果一条直线与一个平面内的______________垂直,那么该直线与此平面垂直
符号语言 l⊥a,l⊥b,a α,b α,__________ l⊥α
图形语言
两条相交直线
a∩b=P
3. 直线和平面所成的角
有关概念 对应图形
斜线 一条直线l与一个平面α相交,但不与这个平面α垂直,图中直线PA
斜足 斜线和平面的交点,图中点A 射影 过斜线上斜足以外的一点P向平面α引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面内的射影 直线与平面所成的角 定义:平面的一条斜线和它在平面上的射影所成的角 规定:一条直线垂直于平面,它们所成的角是直角;一条直线和平面平行或在平面内,它们所成的角是0°的角 取值范围 [0°,90°]
题型突破
典例深度剖析 重点多维探究
题型一 对线面垂直定义及判断定理的理解
[例1] 下列命题中,正确的序号是________.
①若直线l与平面α内的无数条直线垂直,则l⊥α;
②若直线l与平面α内的一条直线垂直,则l⊥α;
③若直线l不垂直于平面α,则α内没有与l垂直的直线;
④若直线l不垂直于平面α,则α内也可以有无数条直线与l垂直;
⑤过一点和已知平面垂直的直线有且只有一条.
×
×
×
当l与α不垂直时,l可能与α内的无数条平行直线垂直
√
√
④⑤
总结提升
(1)证明线面垂直
若一条直线与一个平面内任意一条直线都垂直,则该直线与已知平面垂直.即线线垂直 线面垂直.
(2)证明线线垂直
若一条直线与一个平面垂直,则该直线与平面内任意一条直线垂直.即线面垂直 线线垂直.
直线与平面垂直定义的“双向”作用
跟踪训练
1. 如果一条直线垂直于一个平面内的:①三角形的两边;②梯形的两边;③圆的两条直径;④正五边形的两边.能保证该直线与平面垂直的是________.(填序号)
根据直线与平面垂直的判定定理,平面内这两条直线必须是相交的,
①③④中给定的两直线一定相交,能保证直线与平面垂直,
②梯形的两边可能是上、下底边,它们互相平行,不满足定理条件.
①③④
题型二 线面垂直判定定理的应用
[例2] 如图所示,直角△ABC所在的平面外一点S,SA=SB=SC,点D为斜边AC的中点.求证:直线SD⊥平面ABC.
[证明] ∵SA=SC,点D为斜边AC的中点,
在Rt△ABC中,则AD=DC=BD,
∴△ADS≌△BDS,
∴∠ADS=∠BDS,
∴SD⊥BD. 又AC∩BD=D,
∴SD⊥平面ABC.
∴SD⊥AC.
如图,连接BD,
总结提升
线线垂直和线面垂直的相互转化
多维探究
1.[变条件,变结论]在本例中,若AB=BC,其他条件不变,则BD与平面SAC的位置关系是什么?
∵AB=BC,点D为斜边AC的中点,
∴BD⊥AC.
又由例题知SD⊥BD.
于是BD垂直于平面SAC内的两条相交直线,
故BD⊥平面SAC.
2. [变条件,变结论]将本例改为:已知四棱锥P -ABCD的底面是菱形,且PA=PC,PB=PD. 若O是AC与BD的交点,求证:PO⊥平面ABCD.
证明:在△PBD中,PB=PD,O为BD的中点,
∴PO⊥BD.
在△PAC中,PA=PC,O为AC的中点,
∴PO⊥AC,
又∵AC∩BD=O,
∴PO⊥平面ABCD.
题型三 求直线与平面所成的角
[例3] 三棱锥S- ABC的所有棱长都相等且为a,求SA与底面ABC所成角的余弦值.
如图,过S作SO⊥平面ABC于点O,连接AO,BO,CO.
则SO⊥AO,SO⊥BO,SO⊥CO.
∵SA=SB=SC=a,
∴△SOA≌△SOB≌△SOC,
∴AO=BO=CO,∴O为△ABC的外心.
∵△ABC为正三角形,∴O为△ABC的中心.
∵SO⊥平面ABC,∴∠SAO即为SA与平面ABC所成的角.
在Rt△SAO中,SA=a,AO=×a=a,
∴cos∠SAO= = ,∴SA与底面ABC所成角的余弦值为.
总结提升
(1)寻找过斜线上一点与平面垂直的直线.
(2)连接垂足和斜足得到斜线在平面上的射影,斜线与其射影所成的锐角或直角即为所求的角.
(3)把该角归结在某个三角形中,通过解三角形,求出该角.
求直线与平面所成角的一般步骤
跟踪训练
3. 在正方体ABCD- A1B1C1D1中,
(1)直线A1B与平面ABCD所成的角的大小为_______;
由线面角定义知,∠A1BA为A1B与平面ABCD所成的角,∠A1BA=45°.
45°
跟踪训练
3. 在正方体ABCD- A1B1C1D1中,
(2)直线A1B与平面ABC1D1所成的角的大小为________;
如图,连接A1D,设A1D∩AD1=O,连接BO,
则易证A1D⊥平面ABC1D1,
∴A1B在平面ABC1D1内的射影为OB,
∴A1B与平面ABC1D1所成的角为∠A1BO.
∵A1O= A1B,
∴∠A1BO=30°.
30°
跟踪训练
3. 在正方体ABCD- A1B1C1D1中,
(3)直线A1B与平面AB1C1D所成的角的大小为______.
∵A1B⊥AB1,A1B⊥B1C1,
∴A1B⊥平面AB1C1D,
即A1B与平面AB1C1D所成的角的大小为90°.
90°
随堂检测
1. 直线l⊥平面α,直线m α,则l与m不可能( )
A.平行 B.相交 C.异面 D.垂直
若l∥
l α
m α
l∥
与l⊥α矛盾
l与m不可能平行
A
2.垂直于梯形两腰的直线与梯形所在平面的位置关系是( )
A.垂直 B.相交但不垂直
C.平行 D.不确定
因为梯形两腰所在直线为两条相交直线,
所以由线面垂直的判定定理知,直线与平面垂直.
A
3.如图所示,若斜线段AB是它在平面α上的射影BO的2倍,则AB与平面α所成的角是( )
A.60° B.45°
C.30° D.120°
∠ABO即是斜线AB与平面α所成的角,
在Rt△AOB中,AB=2BO,
所以cos∠ABO= ,
即∠ABO=60°.
A
4.在正方体ABCD -A1B1C1D1中,求证:A1C⊥平面BC1D.
[证明] 如图,连接AC,∴AC⊥BD,
又∵BD⊥A1A,AC∩AA1=A,
AC,A1A 平面A1AC,
∴BD⊥平面A1AC,
∵A1C 平面A1AC,
∴BD⊥A1C.
同理可证BC1⊥A1C.
又∵BD∩BC1=B,BD,BC1 平面BC1D,
∴A1C⊥平面BC1D.
本课小结
1.对直线与平面垂直的几点说明
(1)定义中的“任意一条直线”这一词语与“所有直线”是同义语,与“无数条直线”不是同义语.
(2)直线与平面垂直是直线与平面相交的一种特殊情形.
(3)由直线与平面垂直的定义,得如果一条直线垂直于一个平面,那么这条直线垂直于该平面内的任意一条直线.这是判断两条直线垂直的一种重要方法.
本课小结
2.理解直线与平面垂直的判定定理
不能用“一条直线与平面内的两条平行直线垂直来判断此直线与平面垂直”.实际上,由基本事实4可知,平行具有“传递性”,因此一条直线与平面内的一条直线垂直,那么它与这个平面内平行于这条直线的所有直线都垂直,但不能保证与其他直线平行.
3.判定定理所体现的数学思想
直线与平面垂直的判定定理体现了“转化”的数学思想,即将线面垂直转化为线线垂直.
本课小结
4.直线与平面所成的角的理解和判断
(1)对斜线和平面所成的角的定义的理解
斜线和平面所成的角定义表明斜线和平面所成的角是通过斜线在平面内的射影而转化为两条相交直线所成的角.
(2)判断方法
首先,判断直线和平面的位置,若直线在平面内或与平面平行,此时直线与平面所成的角为0°的角;若直线与平面垂直,此时直线与平面所成的角为90°.
其次,若直线与平面斜交,可在斜线上任取一点作平面的垂线(实际操作过程中,这一点的选取要有利于求角),找出直线在平面内的射影,从而确定出直线和平面所成的角,一般转化到直角三角形、等边三角形中求解.
通过本节课,你学会了什么?
8.6.2 直线与平面垂直(1)
高一
必修二
本节目标
1.借助长方体,通过直观感知、了解空间中直线与平面垂直,理解直线与平面垂直的定义.
2.理解直线与平面垂直的判定定理,并会用其判断直线与平面垂直.
3.理解直线与平面所成角的概念,并能解决简单的线面角问题.
预习课本P149~152,思考并完成以下问题
3.直线与平面所成的角是怎样定义的?直线与平面所成的角的范围是什么?
课前预习
1.直线与平面垂直的定义是怎样的?
2.直线与平面垂直的判定定理是什么?
1.下列说法中,正确的个数是( )
课前小测
①若直线l与平面α内的一条直线垂直,则l⊥α;
②若直线l与平面α内的两条直线垂直,则l⊥α;
③若直线l与平面α内的两条相交直线垂直,则l⊥α;
④若直线l与平面α内的任意一条直线垂直,则l⊥α.
该直线与平面可能平行,也可能斜交,也可能在平面内
该直线与平面可能平行,也可能斜交,也可能在平面内
B
A.4 B.2 C.3 D.1
×
×
√
√
2.若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
A.平面OAB B.平面OAC
C.平面OBC D.平面ABC
O
B
C
A
C
3.一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( )
A.平行 B.垂直
C.相交不垂直 D.不确定
B
一条直线和三角形的两边同时垂直
这条直线垂直三角形所在平面
这条直线垂直第三边
4.在正方体ABCD- A1B1C1D1中,直线AB1与平面ABCD所成的角等于________.
如图,正方体ABCD- A1B1C1D1中,B1B⊥平面ABCD,
所以AB即为AB1在平面ABCD中的射影,
∠B1AB即为直线AB1与平面ABCD所成的角.
由题意知,∠B1AB=45°,故所求角为45°.
45°
新课导入
空间中直线与平面有几种位置关系?
α
a
α
a
A
α
a
a
a∥
a=A
生活中有很多直线与平面垂直的实例
新知探究
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直?
A
B
请给直线与平面垂直下定义.
A
B
直线垂直于平面内任意一条直线.
任意一条
1.直线与平面垂直
定义 如果直线l与平面α内的___________直线都垂直,我们就说直线l与平面α互相垂直
记法 l⊥α
有关概念 直线l叫做平面α的______,平面α叫做直线l的_______.它们唯一的公共点P叫做________.
图示
画法 画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
任意一条
垂线
垂面
垂足
线面垂直的定义常这样使用
α
l
a
l⊥α
a
l⊥a
简记:若线面垂直,则线线垂直
思考
?
在同一平面内,过一点有且只有一条直线与已知直线垂直,将这一结论推广到空间,过一点垂直于已知平面的直线有几条?为什么?
过一点垂直于已知平面的直线有且只有一条.
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
探究
如图,准备一块三角形的硬纸片,做一个试验:
A
B
C
D
过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触).
问题:(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在平面垂直?
A
B
C
D
α
A
C
D
B
当且仅当折痕AD是BC边上的高时,AD所在直线与桌面所在平面α垂直.
2. 直线与平面垂直的判定定理
文字语言 如果一条直线与一个平面内的______________垂直,那么该直线与此平面垂直
符号语言 l⊥a,l⊥b,a α,b α,__________ l⊥α
图形语言
两条相交直线
a∩b=P
3. 直线和平面所成的角
有关概念 对应图形
斜线 一条直线l与一个平面α相交,但不与这个平面α垂直,图中直线PA
斜足 斜线和平面的交点,图中点A 射影 过斜线上斜足以外的一点P向平面α引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面内的射影 直线与平面所成的角 定义:平面的一条斜线和它在平面上的射影所成的角 规定:一条直线垂直于平面,它们所成的角是直角;一条直线和平面平行或在平面内,它们所成的角是0°的角 取值范围 [0°,90°]
题型突破
典例深度剖析 重点多维探究
题型一 对线面垂直定义及判断定理的理解
[例1] 下列命题中,正确的序号是________.
①若直线l与平面α内的无数条直线垂直,则l⊥α;
②若直线l与平面α内的一条直线垂直,则l⊥α;
③若直线l不垂直于平面α,则α内没有与l垂直的直线;
④若直线l不垂直于平面α,则α内也可以有无数条直线与l垂直;
⑤过一点和已知平面垂直的直线有且只有一条.
×
×
×
当l与α不垂直时,l可能与α内的无数条平行直线垂直
√
√
④⑤
总结提升
(1)证明线面垂直
若一条直线与一个平面内任意一条直线都垂直,则该直线与已知平面垂直.即线线垂直 线面垂直.
(2)证明线线垂直
若一条直线与一个平面垂直,则该直线与平面内任意一条直线垂直.即线面垂直 线线垂直.
直线与平面垂直定义的“双向”作用
跟踪训练
1. 如果一条直线垂直于一个平面内的:①三角形的两边;②梯形的两边;③圆的两条直径;④正五边形的两边.能保证该直线与平面垂直的是________.(填序号)
根据直线与平面垂直的判定定理,平面内这两条直线必须是相交的,
①③④中给定的两直线一定相交,能保证直线与平面垂直,
②梯形的两边可能是上、下底边,它们互相平行,不满足定理条件.
①③④
题型二 线面垂直判定定理的应用
[例2] 如图所示,直角△ABC所在的平面外一点S,SA=SB=SC,点D为斜边AC的中点.求证:直线SD⊥平面ABC.
[证明] ∵SA=SC,点D为斜边AC的中点,
在Rt△ABC中,则AD=DC=BD,
∴△ADS≌△BDS,
∴∠ADS=∠BDS,
∴SD⊥BD. 又AC∩BD=D,
∴SD⊥平面ABC.
∴SD⊥AC.
如图,连接BD,
总结提升
线线垂直和线面垂直的相互转化
多维探究
1.[变条件,变结论]在本例中,若AB=BC,其他条件不变,则BD与平面SAC的位置关系是什么?
∵AB=BC,点D为斜边AC的中点,
∴BD⊥AC.
又由例题知SD⊥BD.
于是BD垂直于平面SAC内的两条相交直线,
故BD⊥平面SAC.
2. [变条件,变结论]将本例改为:已知四棱锥P -ABCD的底面是菱形,且PA=PC,PB=PD. 若O是AC与BD的交点,求证:PO⊥平面ABCD.
证明:在△PBD中,PB=PD,O为BD的中点,
∴PO⊥BD.
在△PAC中,PA=PC,O为AC的中点,
∴PO⊥AC,
又∵AC∩BD=O,
∴PO⊥平面ABCD.
题型三 求直线与平面所成的角
[例3] 三棱锥S- ABC的所有棱长都相等且为a,求SA与底面ABC所成角的余弦值.
如图,过S作SO⊥平面ABC于点O,连接AO,BO,CO.
则SO⊥AO,SO⊥BO,SO⊥CO.
∵SA=SB=SC=a,
∴△SOA≌△SOB≌△SOC,
∴AO=BO=CO,∴O为△ABC的外心.
∵△ABC为正三角形,∴O为△ABC的中心.
∵SO⊥平面ABC,∴∠SAO即为SA与平面ABC所成的角.
在Rt△SAO中,SA=a,AO=×a=a,
∴cos∠SAO= = ,∴SA与底面ABC所成角的余弦值为.
总结提升
(1)寻找过斜线上一点与平面垂直的直线.
(2)连接垂足和斜足得到斜线在平面上的射影,斜线与其射影所成的锐角或直角即为所求的角.
(3)把该角归结在某个三角形中,通过解三角形,求出该角.
求直线与平面所成角的一般步骤
跟踪训练
3. 在正方体ABCD- A1B1C1D1中,
(1)直线A1B与平面ABCD所成的角的大小为_______;
由线面角定义知,∠A1BA为A1B与平面ABCD所成的角,∠A1BA=45°.
45°
跟踪训练
3. 在正方体ABCD- A1B1C1D1中,
(2)直线A1B与平面ABC1D1所成的角的大小为________;
如图,连接A1D,设A1D∩AD1=O,连接BO,
则易证A1D⊥平面ABC1D1,
∴A1B在平面ABC1D1内的射影为OB,
∴A1B与平面ABC1D1所成的角为∠A1BO.
∵A1O= A1B,
∴∠A1BO=30°.
30°
跟踪训练
3. 在正方体ABCD- A1B1C1D1中,
(3)直线A1B与平面AB1C1D所成的角的大小为______.
∵A1B⊥AB1,A1B⊥B1C1,
∴A1B⊥平面AB1C1D,
即A1B与平面AB1C1D所成的角的大小为90°.
90°
随堂检测
1. 直线l⊥平面α,直线m α,则l与m不可能( )
A.平行 B.相交 C.异面 D.垂直
若l∥
l α
m α
l∥
与l⊥α矛盾
l与m不可能平行
A
2.垂直于梯形两腰的直线与梯形所在平面的位置关系是( )
A.垂直 B.相交但不垂直
C.平行 D.不确定
因为梯形两腰所在直线为两条相交直线,
所以由线面垂直的判定定理知,直线与平面垂直.
A
3.如图所示,若斜线段AB是它在平面α上的射影BO的2倍,则AB与平面α所成的角是( )
A.60° B.45°
C.30° D.120°
∠ABO即是斜线AB与平面α所成的角,
在Rt△AOB中,AB=2BO,
所以cos∠ABO= ,
即∠ABO=60°.
A
4.在正方体ABCD -A1B1C1D1中,求证:A1C⊥平面BC1D.
[证明] 如图,连接AC,∴AC⊥BD,
又∵BD⊥A1A,AC∩AA1=A,
AC,A1A 平面A1AC,
∴BD⊥平面A1AC,
∵A1C 平面A1AC,
∴BD⊥A1C.
同理可证BC1⊥A1C.
又∵BD∩BC1=B,BD,BC1 平面BC1D,
∴A1C⊥平面BC1D.
本课小结
1.对直线与平面垂直的几点说明
(1)定义中的“任意一条直线”这一词语与“所有直线”是同义语,与“无数条直线”不是同义语.
(2)直线与平面垂直是直线与平面相交的一种特殊情形.
(3)由直线与平面垂直的定义,得如果一条直线垂直于一个平面,那么这条直线垂直于该平面内的任意一条直线.这是判断两条直线垂直的一种重要方法.
本课小结
2.理解直线与平面垂直的判定定理
不能用“一条直线与平面内的两条平行直线垂直来判断此直线与平面垂直”.实际上,由基本事实4可知,平行具有“传递性”,因此一条直线与平面内的一条直线垂直,那么它与这个平面内平行于这条直线的所有直线都垂直,但不能保证与其他直线平行.
3.判定定理所体现的数学思想
直线与平面垂直的判定定理体现了“转化”的数学思想,即将线面垂直转化为线线垂直.
本课小结
4.直线与平面所成的角的理解和判断
(1)对斜线和平面所成的角的定义的理解
斜线和平面所成的角定义表明斜线和平面所成的角是通过斜线在平面内的射影而转化为两条相交直线所成的角.
(2)判断方法
首先,判断直线和平面的位置,若直线在平面内或与平面平行,此时直线与平面所成的角为0°的角;若直线与平面垂直,此时直线与平面所成的角为90°.
其次,若直线与平面斜交,可在斜线上任取一点作平面的垂线(实际操作过程中,这一点的选取要有利于求角),找出直线在平面内的射影,从而确定出直线和平面所成的角,一般转化到直角三角形、等边三角形中求解.
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
