人教版(2019)数学必修第二册9_2_1总体取值规律的估计 课件(共49张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册9_2_1总体取值规律的估计 课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 965.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 00:00:00 | ||
图片预览











文档简介
(共49张PPT)
9.2.1 总体取值规律的估计
高一
必修二
本节目标
1.会列频率分布表,会画频率分布直方图,理解它们的特点.
2. 会用样本的频率分布估计总体分布.
3.会用随机抽样的基本方法和用样本估计总体的思想解决一些简单的实际问题.
预习课本P192~200,思考并完成以下问题
我们学过哪些统计图?它们各有什么特点?
(2) 画频率分布直方图可分为哪些步骤?
课前预习
(1)频率分布直方图的纵轴表示频率.( )
课前小测
1.判一判(正确的打“√”,错误的打“×”)
×
(2)数据落在各小组内的频率用来表示.( )
√
(3)频率分布直方图把样本数据落在各小组的比例大小直观化,更有利于我们从整体上把握数据分布的特点.( )
√
频率/组距
2.做一做
(1)将容量为100的样本数据分为8个组,如下表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
A.0.03 B.0.07 C.0.14 D.0.21
则第3组的频率为( )
C
x =100-(10+13+14+15+13+12+9)
=100-86
=14
第3组的频率为=0.14
(2)一个容量为n的样本,分成若干组,已知某组的频率和频数分别为0.125和40,则n的值为( )
A.640 B.320
C.240 D.160
B
n=320
(3)一个容量为20的样本,分组后,组距与频数如下:
[10,20),2;[20,30),3;[30,40),4;[40,50),5;[50,60),4;[60,70],2,
则样本在[10,50)上的频率为( )
A. B. C. D.
D
=
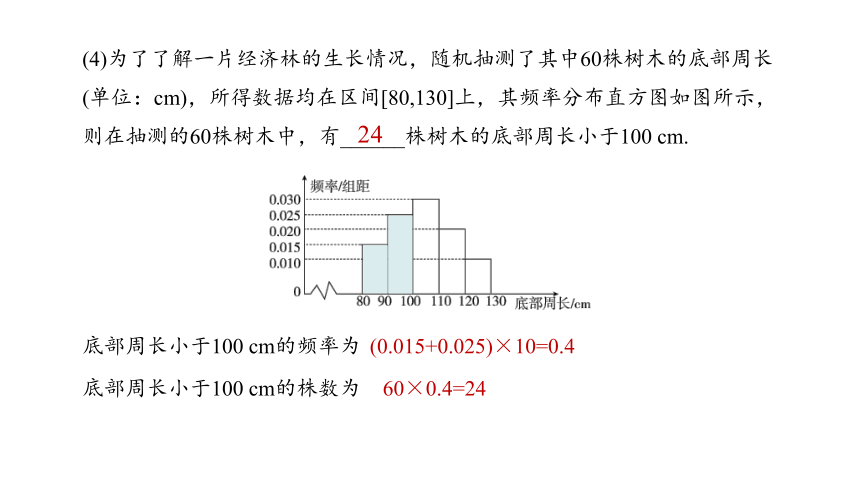
(4)为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有______株树木的底部周长小于100 cm.
24
(0.015+0.025)×10=0.4
底部周长小于100 cm的频率为
底部周长小于100 cm的株数为
60×0.4=24
新知探究
一、怎样研究总体的取值规律
对一个统计问题,在随机抽样获得观测数据的基础上,需要根据数据分析的需要,选择适当的统计图表描述和表示数据,获得样本的规律,并利用样本的规律估计总体的规律,解决相应的实际问题.
二、频率分布表与频率分布直方图
1.频率分布表
一般地,当总体很大或不便获取时,用样本的频率分布估计总体的频率分布.把反应总体频率分布的表格称为频率分布表.
2.频率分布直方图
把表示样本数据分布规律的图形称为频率分布直方图.
3.制作频率分布表与频率分布直方图的一般步骤:
(1)求极差,即计算___________________.
(2)决定______________.
(3)将数据____________.
(4)列________________.
(5)画频率分布直方图.
最大值与最小值的差
组距与组数
分组
频率分布表
三、常用的统计图
1.条形图
条形图能清楚地表示出每个项目的____________.
2.折线图
折线图能够清晰地反映数据的___________________.
3.扇形图
扇形图能直观、生动地反映各部分在总体中所占的_______情况.
具体数量
变化趋势或情况
比例
频率分布直方图把样本数据落在各小组的比例大小直观化,更有利于我们从整体上把握数据分布的特点.
各小长方形的面积表示相应各组的频率. 这样,频率分布直方图就以面积的形式反映了数据落在各个小组的频率的大小.
在频率分布直方图中,各小长方形的面积的总和等于1,即样本数据落在整个区间的频率为1.
?
思考
频率分布直方图有什么特点?
四、频率分布表和频率分布直方图的优缺点
(2) 频率分布直方图能够直观地表明数据分布的形状,一般呈中间高、两端低、左右对称的“峰”状结构.但是从直方图本身得不到具体的数据内容,也就是说,将数据表示成直方图以后,原始数据不能在图中表示出来.
(1) 频率分布表反映具体数据在各个不同区间的取值频率,但不够直观、形象,对分析数据分布的总体态势不太方便.
题型突破
典例深度剖析 重点多维探究
题型一 频率分布直方图的画法
[例1] 从某校高一年级1002名新生中随机抽取一个容量为100的身高样本,数据如下(单位:cm),试作出该样本的频率分布表和频率分布直方图.
168 165 171 167 170 165 170 152 175 174
165 170 168 169 171 166 164 155 164 158
170 155 166 158 155 160 160 164 156 162
160 170 168 164 174 171 165 179 163 172
180 174 168 164 174 171 165 179 163 169
151 168 158 168 176 155 165 165 169 162
177 158 175 165 169 151 163 166 163 167
178 165 158 170 169 159 155 163 153 155
167 163 164 158 168 167 161 162 167 168
161 165 174 156 167 166 162 161 164 166
168 165 171 167 170 165 170 152 175 174
165 170 168 169 171 166 164 155 164 158
170 155 166 158 155 160 160 164 156 162
160 170 168 164 174 171 165 179 163 172
180 174 168 164 174 171 165 179 163 169
151 168 158 168 176 155 165 165 169 162
177 158 175 165 169 151 163 166 163 167
178 165 158 170 169 159 155 163 153 155
167 163 164 158 168 167 161 162 167 168
161 165 174 156 167 166 162 161 164 166
(1) 在全部数据中找出最大值180,最小值151,计算极差=180-151=29.
(2) 取组距为3,则组数为≈10.
(3) 从第一组[150.5,153.5)开始,统计出各组的频数,再计算各组的频率,并将结果填入下表:
频率分布直方图如图
总结提升
(1) 计算极差,需要找出这组数的最大值和最小值,当数据很多时,可选一个数当参照.
(2) 将一批数据分组,目的是要描述数据分布规律,要根据数据多少来确定分组数目,一般来说,数据越多,分组越多.
(3) 将数据分组,决定分点时,一般使分点比数据多一位小数,并且把第一组的起点稍微减小一点.
(4) 列频率分布表时,可通过逐一判断各个数据落在哪个小组内,以“正”字确定各个小组内数据的个数.
(5) 画频率分布直方图时,纵坐标表示频率与组距的比值,一定不能标成频率.
绘制频率分布直方图的注意事项
跟踪训练
1.美国历届总统中,就任时年龄最小的是罗斯福,他于1901年就任,当时年仅42岁;就任时年龄最大的是特朗普,他于2016年就任,当时70岁.下面按时间顺序(从1789年的华盛顿到2016年的特朗普,共45任)给出了历届美国总统就任时的年龄:
57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,
52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,
54,51,60,62,43,55,56,61,52,69,64,46,54,47,70.
(1)将数据分为7组,列出频率分布表,并画出相应的频率分布直方图;
(2)用自己的语言描述一下历届美国总统就任时年龄的分布情况.
(1)以4为组距,列频率分布表如下
分组 频数 频率
[42,46) 2 0.0444
[46,50) 7 0.1555
[50,54) 8 0.1778
[54,58) 16 0.3556
[58,62) 5 0.1111
[62,66) 4 0.0889
[66,70] 3 0.0667
合计 45 1.0000
画出相应的频率分布直方图,如图所示.
(2)从频率分布表中可以看出,将近60%的美国总统就任时的年龄在50岁至60岁之间,45岁及45岁以下和65岁以上就任的总统所占的比例相对较小.
题型二 频率分布直方图的应用
[例2] 为了迎接某市作为全国文明城市的复查,爱卫会随机抽取了60位路人进行问卷调查,调查项目是自己对该市各方面卫生情况的满意度(假设被问卷的路人回答是客观的),以分数表示问卷结果,并统计他们的问卷分数,把其中不低于50分的分成五段:[50,60),[60,70),…,[90,100]后画出如图所示的部分频率分布直方图,观察图形信息,回答下列问题:
(1)求出问卷调查分数低于50分的被问卷人数;
(2)估计全市市民满意度在60分及以上的百分比.
(1)求出问卷调查分数低于50分的被问卷人数;
因为各组的频率之和等于1,
故低于50分的频率为
f=1-(0.015×2+0.030+0.025+0.005)×10 =0.1,
故低于50分的人数为60×0.1=6.
(2)估计全市市民满意度在60分及以上的百分比.
依题意,60分及以上的频率和为
(0.015+0.030+0.025+0.005)×10=0.75,
所以抽样满意度在60分及以上的百分比为75%.
于是,可以估计全市市民满意度在60分及以上的百分比为75%.
(2)频率分布直方图中,各个小长方形的面积等于频率,各个小长方形的面积之和为1;
频率分布指的是一个样本数据在各个小范围内所占比例的大小,一般用频率分布直方图反映样本的频率分布,其中:
(1)频率分布直方图中纵轴表示;
(3)长方形的高的比也就是频率之比.
总结提升
频率分布直方图的应用
跟踪训练
2.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图所示),由图中数据可知a=________.若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为________.
因为频率分布直方图中各小长方形的面积之和为1,
所以10×(0.005+0.035+a+0.020+0.010)=1,
解得a=0.030.
0.030
跟踪训练
2.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图所示),由图中数据可知a=________.若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为________.
0.030
由图可知身高在[120,150]内的学生人数为
100×10×(0.030+0.020+0.010)=60,
其中身高在[140,150]内的学生人数为10,
所以从身高在[140,150]内的学生中选取的人数为×10=3.
3
题型三 统计图表的应用
[例3] 某省有关部门要求各中小学要把“每天锻炼一小时”写入课程表,为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的柱形图.请结合柱形图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
(1)该校对多少名学生进行了抽样调查?
由图1知4+8+10+18+10=50(名),
所以该校对50名学生进行了抽样调查.
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
本次调查中,最喜欢篮球活动的有18人
占被调查人数的×100%=36%.
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
所以估计全校学生中最喜欢跳绳活动的人数约为160.
1-(30%+26%+24%)=20%,
200÷20%=1000(人),
×100%×1000=160(人),
总结提升
(1)柱形图是用一个单位长度表示一定的数量,根据数量的多少画成高度不同的小矩形,然后把这些小矩形按照一定的顺序排列起来.其特点是便于看出和比较各种数量的多少,即柱形图能清楚地表示出每个项目的具体数目.
(2)扇形图是用整个圆面积表示总数(100%),用圆内的扇形面积表示各部分所占总数的百分数.
总之,用图表来表示数量关系更生动形象、具体,使人一目了然.
跟踪训练
3. 下表给出了2018年A,B两地的降水量(单位:mm):
(1)根据统计表绘制折线图;
(2)根据折线图比较A,B两地的降水量,分析哪个地方的降水量较大?
(1)根据统计表绘制折线图;
建立直角坐标系,用横坐标上的点表示月份,用纵坐标上的点表示降水量,描出每个月份对应的点,然后用直线段顺次连接相邻的点,得到折线统计图如图表示.
(2)根据折线图比较A,B两地的降水量,分析哪个地方的降水量较大?
观察折线图,从整体上看,B地降水量较大.
随堂检测
1.反映某种股票的涨跌情况,应选择( )
A.条形图 B.折线图
C.扇形图 D.三种图均可
条形图主要用于直观描述不同类别或分组数据的频数.
折线图主要用于描述数据随时间变化的趋势.
扇形图主要用于直观描述各类数据占总数的比例.
B
2.为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
A.6 B.8
C.12 D.18
C
志愿者的总人数为=50,
所以第三组的人数为50×0.36×1=18,
所以有疗效的人数为18-6=12.
3.一个频率分布表(样本量为30)不小心被损坏了一部分,只记得样本中数据在[20,60)内的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数共为( )
A.14 B.15 C.16 D.17
∵样本中数据在[20,60)内的频率为0.8,
∴样本数据在[20,60)内的频数为30×0.8=24,
∴样本在[40,50),[50,60)内的数据个数共为24-4-5=15.
B
4.某电子商务公司对10000名网络购物者2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=________;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为________.
由频率分布直方图及频率和等于1可得
0.2×0.1+0.8×0.1+1.5×0.1+2.0×0.1+2.5×0.1+a×0.1=1
(1)直方图中的a=________;
解得a=3.0
3.0
消费金额在区间[0.5,0.9]内的频率为
0.2×0.1+0.8×0.1+2.0×0.1+3.0×0.1=0.6,
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为________.
所以消费金额在区间[0.5,0.9]内的购物者的人数为0.6×10000=6000.
6000
5.从高三参加数学竞赛的学生中抽取50名学生的成绩,成绩的分组及各组的频数如下(单位:分):
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计成绩在[60,90)分的学生比例;
(4)估计成绩在80分以下的学生比例.
(1)频率分布表如下:
成绩分组 频数 频率
[40,50) 2 0.04
[50,60) 3 0.06
[60,70) 10 0.2
[70,80) 15 0.3
[80,90) 12 0.24
[90,100] 8 0.16
合计 50 1
(2)频率分布直方图如图所示.
样本中成绩在[60,90)分的学生比例为0.20+0.30+0.24=0.74=74%.
(3)估计成绩在[60,90)分的学生比例;
由样本估计总体,成绩在[60,90)分的学生约占74%.
样本中成绩在80分以下学生比例为1-(0.24+0.16)=1-0.4=0.6=60% .
(4)估计成绩在80分以下的学生比例.
由样本估计总体,成绩在80分以下的学生约占60%.
本课小结
2.条形统计图及折线统计图特别适用于数据量很大的情况,但却损失了数据的部分信息.扇形统计图适合表示总体的各个部分所占比例的问题,但不适用于总体分成部分较多的问题.
1.样本数据的频率分布表和频率分布直方图,是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律,它可以让我们更清楚地看到整个样本数据的频率分布情况,并由此估计总体的分布情况.
通过本节课,你学会了什么?
9.2.1 总体取值规律的估计
高一
必修二
本节目标
1.会列频率分布表,会画频率分布直方图,理解它们的特点.
2. 会用样本的频率分布估计总体分布.
3.会用随机抽样的基本方法和用样本估计总体的思想解决一些简单的实际问题.
预习课本P192~200,思考并完成以下问题
我们学过哪些统计图?它们各有什么特点?
(2) 画频率分布直方图可分为哪些步骤?
课前预习
(1)频率分布直方图的纵轴表示频率.( )
课前小测
1.判一判(正确的打“√”,错误的打“×”)
×
(2)数据落在各小组内的频率用来表示.( )
√
(3)频率分布直方图把样本数据落在各小组的比例大小直观化,更有利于我们从整体上把握数据分布的特点.( )
√
频率/组距
2.做一做
(1)将容量为100的样本数据分为8个组,如下表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
A.0.03 B.0.07 C.0.14 D.0.21
则第3组的频率为( )
C
x =100-(10+13+14+15+13+12+9)
=100-86
=14
第3组的频率为=0.14
(2)一个容量为n的样本,分成若干组,已知某组的频率和频数分别为0.125和40,则n的值为( )
A.640 B.320
C.240 D.160
B
n=320
(3)一个容量为20的样本,分组后,组距与频数如下:
[10,20),2;[20,30),3;[30,40),4;[40,50),5;[50,60),4;[60,70],2,
则样本在[10,50)上的频率为( )
A. B. C. D.
D
=
(4)为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有______株树木的底部周长小于100 cm.
24
(0.015+0.025)×10=0.4
底部周长小于100 cm的频率为
底部周长小于100 cm的株数为
60×0.4=24
新知探究
一、怎样研究总体的取值规律
对一个统计问题,在随机抽样获得观测数据的基础上,需要根据数据分析的需要,选择适当的统计图表描述和表示数据,获得样本的规律,并利用样本的规律估计总体的规律,解决相应的实际问题.
二、频率分布表与频率分布直方图
1.频率分布表
一般地,当总体很大或不便获取时,用样本的频率分布估计总体的频率分布.把反应总体频率分布的表格称为频率分布表.
2.频率分布直方图
把表示样本数据分布规律的图形称为频率分布直方图.
3.制作频率分布表与频率分布直方图的一般步骤:
(1)求极差,即计算___________________.
(2)决定______________.
(3)将数据____________.
(4)列________________.
(5)画频率分布直方图.
最大值与最小值的差
组距与组数
分组
频率分布表
三、常用的统计图
1.条形图
条形图能清楚地表示出每个项目的____________.
2.折线图
折线图能够清晰地反映数据的___________________.
3.扇形图
扇形图能直观、生动地反映各部分在总体中所占的_______情况.
具体数量
变化趋势或情况
比例
频率分布直方图把样本数据落在各小组的比例大小直观化,更有利于我们从整体上把握数据分布的特点.
各小长方形的面积表示相应各组的频率. 这样,频率分布直方图就以面积的形式反映了数据落在各个小组的频率的大小.
在频率分布直方图中,各小长方形的面积的总和等于1,即样本数据落在整个区间的频率为1.
?
思考
频率分布直方图有什么特点?
四、频率分布表和频率分布直方图的优缺点
(2) 频率分布直方图能够直观地表明数据分布的形状,一般呈中间高、两端低、左右对称的“峰”状结构.但是从直方图本身得不到具体的数据内容,也就是说,将数据表示成直方图以后,原始数据不能在图中表示出来.
(1) 频率分布表反映具体数据在各个不同区间的取值频率,但不够直观、形象,对分析数据分布的总体态势不太方便.
题型突破
典例深度剖析 重点多维探究
题型一 频率分布直方图的画法
[例1] 从某校高一年级1002名新生中随机抽取一个容量为100的身高样本,数据如下(单位:cm),试作出该样本的频率分布表和频率分布直方图.
168 165 171 167 170 165 170 152 175 174
165 170 168 169 171 166 164 155 164 158
170 155 166 158 155 160 160 164 156 162
160 170 168 164 174 171 165 179 163 172
180 174 168 164 174 171 165 179 163 169
151 168 158 168 176 155 165 165 169 162
177 158 175 165 169 151 163 166 163 167
178 165 158 170 169 159 155 163 153 155
167 163 164 158 168 167 161 162 167 168
161 165 174 156 167 166 162 161 164 166
168 165 171 167 170 165 170 152 175 174
165 170 168 169 171 166 164 155 164 158
170 155 166 158 155 160 160 164 156 162
160 170 168 164 174 171 165 179 163 172
180 174 168 164 174 171 165 179 163 169
151 168 158 168 176 155 165 165 169 162
177 158 175 165 169 151 163 166 163 167
178 165 158 170 169 159 155 163 153 155
167 163 164 158 168 167 161 162 167 168
161 165 174 156 167 166 162 161 164 166
(1) 在全部数据中找出最大值180,最小值151,计算极差=180-151=29.
(2) 取组距为3,则组数为≈10.
(3) 从第一组[150.5,153.5)开始,统计出各组的频数,再计算各组的频率,并将结果填入下表:
频率分布直方图如图
总结提升
(1) 计算极差,需要找出这组数的最大值和最小值,当数据很多时,可选一个数当参照.
(2) 将一批数据分组,目的是要描述数据分布规律,要根据数据多少来确定分组数目,一般来说,数据越多,分组越多.
(3) 将数据分组,决定分点时,一般使分点比数据多一位小数,并且把第一组的起点稍微减小一点.
(4) 列频率分布表时,可通过逐一判断各个数据落在哪个小组内,以“正”字确定各个小组内数据的个数.
(5) 画频率分布直方图时,纵坐标表示频率与组距的比值,一定不能标成频率.
绘制频率分布直方图的注意事项
跟踪训练
1.美国历届总统中,就任时年龄最小的是罗斯福,他于1901年就任,当时年仅42岁;就任时年龄最大的是特朗普,他于2016年就任,当时70岁.下面按时间顺序(从1789年的华盛顿到2016年的特朗普,共45任)给出了历届美国总统就任时的年龄:
57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,
52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,
54,51,60,62,43,55,56,61,52,69,64,46,54,47,70.
(1)将数据分为7组,列出频率分布表,并画出相应的频率分布直方图;
(2)用自己的语言描述一下历届美国总统就任时年龄的分布情况.
(1)以4为组距,列频率分布表如下
分组 频数 频率
[42,46) 2 0.0444
[46,50) 7 0.1555
[50,54) 8 0.1778
[54,58) 16 0.3556
[58,62) 5 0.1111
[62,66) 4 0.0889
[66,70] 3 0.0667
合计 45 1.0000
画出相应的频率分布直方图,如图所示.
(2)从频率分布表中可以看出,将近60%的美国总统就任时的年龄在50岁至60岁之间,45岁及45岁以下和65岁以上就任的总统所占的比例相对较小.
题型二 频率分布直方图的应用
[例2] 为了迎接某市作为全国文明城市的复查,爱卫会随机抽取了60位路人进行问卷调查,调查项目是自己对该市各方面卫生情况的满意度(假设被问卷的路人回答是客观的),以分数表示问卷结果,并统计他们的问卷分数,把其中不低于50分的分成五段:[50,60),[60,70),…,[90,100]后画出如图所示的部分频率分布直方图,观察图形信息,回答下列问题:
(1)求出问卷调查分数低于50分的被问卷人数;
(2)估计全市市民满意度在60分及以上的百分比.
(1)求出问卷调查分数低于50分的被问卷人数;
因为各组的频率之和等于1,
故低于50分的频率为
f=1-(0.015×2+0.030+0.025+0.005)×10 =0.1,
故低于50分的人数为60×0.1=6.
(2)估计全市市民满意度在60分及以上的百分比.
依题意,60分及以上的频率和为
(0.015+0.030+0.025+0.005)×10=0.75,
所以抽样满意度在60分及以上的百分比为75%.
于是,可以估计全市市民满意度在60分及以上的百分比为75%.
(2)频率分布直方图中,各个小长方形的面积等于频率,各个小长方形的面积之和为1;
频率分布指的是一个样本数据在各个小范围内所占比例的大小,一般用频率分布直方图反映样本的频率分布,其中:
(1)频率分布直方图中纵轴表示;
(3)长方形的高的比也就是频率之比.
总结提升
频率分布直方图的应用
跟踪训练
2.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图所示),由图中数据可知a=________.若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为________.
因为频率分布直方图中各小长方形的面积之和为1,
所以10×(0.005+0.035+a+0.020+0.010)=1,
解得a=0.030.
0.030
跟踪训练
2.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图所示),由图中数据可知a=________.若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为________.
0.030
由图可知身高在[120,150]内的学生人数为
100×10×(0.030+0.020+0.010)=60,
其中身高在[140,150]内的学生人数为10,
所以从身高在[140,150]内的学生中选取的人数为×10=3.
3
题型三 统计图表的应用
[例3] 某省有关部门要求各中小学要把“每天锻炼一小时”写入课程表,为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的柱形图.请结合柱形图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
(1)该校对多少名学生进行了抽样调查?
由图1知4+8+10+18+10=50(名),
所以该校对50名学生进行了抽样调查.
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
本次调查中,最喜欢篮球活动的有18人
占被调查人数的×100%=36%.
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
所以估计全校学生中最喜欢跳绳活动的人数约为160.
1-(30%+26%+24%)=20%,
200÷20%=1000(人),
×100%×1000=160(人),
总结提升
(1)柱形图是用一个单位长度表示一定的数量,根据数量的多少画成高度不同的小矩形,然后把这些小矩形按照一定的顺序排列起来.其特点是便于看出和比较各种数量的多少,即柱形图能清楚地表示出每个项目的具体数目.
(2)扇形图是用整个圆面积表示总数(100%),用圆内的扇形面积表示各部分所占总数的百分数.
总之,用图表来表示数量关系更生动形象、具体,使人一目了然.
跟踪训练
3. 下表给出了2018年A,B两地的降水量(单位:mm):
(1)根据统计表绘制折线图;
(2)根据折线图比较A,B两地的降水量,分析哪个地方的降水量较大?
(1)根据统计表绘制折线图;
建立直角坐标系,用横坐标上的点表示月份,用纵坐标上的点表示降水量,描出每个月份对应的点,然后用直线段顺次连接相邻的点,得到折线统计图如图表示.
(2)根据折线图比较A,B两地的降水量,分析哪个地方的降水量较大?
观察折线图,从整体上看,B地降水量较大.
随堂检测
1.反映某种股票的涨跌情况,应选择( )
A.条形图 B.折线图
C.扇形图 D.三种图均可
条形图主要用于直观描述不同类别或分组数据的频数.
折线图主要用于描述数据随时间变化的趋势.
扇形图主要用于直观描述各类数据占总数的比例.
B
2.为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
A.6 B.8
C.12 D.18
C
志愿者的总人数为=50,
所以第三组的人数为50×0.36×1=18,
所以有疗效的人数为18-6=12.
3.一个频率分布表(样本量为30)不小心被损坏了一部分,只记得样本中数据在[20,60)内的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数共为( )
A.14 B.15 C.16 D.17
∵样本中数据在[20,60)内的频率为0.8,
∴样本数据在[20,60)内的频数为30×0.8=24,
∴样本在[40,50),[50,60)内的数据个数共为24-4-5=15.
B
4.某电子商务公司对10000名网络购物者2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=________;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为________.
由频率分布直方图及频率和等于1可得
0.2×0.1+0.8×0.1+1.5×0.1+2.0×0.1+2.5×0.1+a×0.1=1
(1)直方图中的a=________;
解得a=3.0
3.0
消费金额在区间[0.5,0.9]内的频率为
0.2×0.1+0.8×0.1+2.0×0.1+3.0×0.1=0.6,
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为________.
所以消费金额在区间[0.5,0.9]内的购物者的人数为0.6×10000=6000.
6000
5.从高三参加数学竞赛的学生中抽取50名学生的成绩,成绩的分组及各组的频数如下(单位:分):
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计成绩在[60,90)分的学生比例;
(4)估计成绩在80分以下的学生比例.
(1)频率分布表如下:
成绩分组 频数 频率
[40,50) 2 0.04
[50,60) 3 0.06
[60,70) 10 0.2
[70,80) 15 0.3
[80,90) 12 0.24
[90,100] 8 0.16
合计 50 1
(2)频率分布直方图如图所示.
样本中成绩在[60,90)分的学生比例为0.20+0.30+0.24=0.74=74%.
(3)估计成绩在[60,90)分的学生比例;
由样本估计总体,成绩在[60,90)分的学生约占74%.
样本中成绩在80分以下学生比例为1-(0.24+0.16)=1-0.4=0.6=60% .
(4)估计成绩在80分以下的学生比例.
由样本估计总体,成绩在80分以下的学生约占60%.
本课小结
2.条形统计图及折线统计图特别适用于数据量很大的情况,但却损失了数据的部分信息.扇形统计图适合表示总体的各个部分所占比例的问题,但不适用于总体分成部分较多的问题.
1.样本数据的频率分布表和频率分布直方图,是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律,它可以让我们更清楚地看到整个样本数据的频率分布情况,并由此估计总体的分布情况.
通过本节课,你学会了什么?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
