人教版(2019)数学必修第二册第九章 统计 单元复习课件(共16张PPT)
文档属性
| 名称 | 人教版(2019)数学必修第二册第九章 统计 单元复习课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 683.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 11:14:40 | ||
图片预览




文档简介
(共16张PPT)
统 计
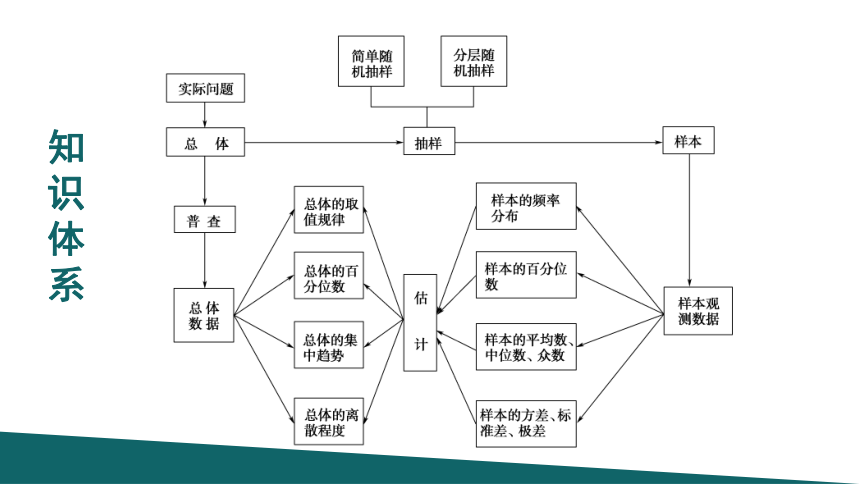
知识体系
题型一 随机抽样方法的应用
专题复习
【例1】 某政府机关有在编人员100人,其中副处级以上干部10人,一般干部70人,干事20人,上级机关为了了解机关人员对政府机构的改革意见,要从中抽取一个容量为20的样本,试确定用何种方法抽取,如何抽取?
即从副处级以上干部中抽取2人,一般干部中抽取14人,干事中抽取4人.
用分层随机抽样抽取.
∵20∶100=1∶5,∴ =2, =14, =4,
∵副处级以上干部与干事人数都较少,他们分别按1~10编号和1~20编号,然后采用抽签法分别抽取2人和4人,对一般干部采用00,01,…,69编号,然后用随机数法抽取14人.
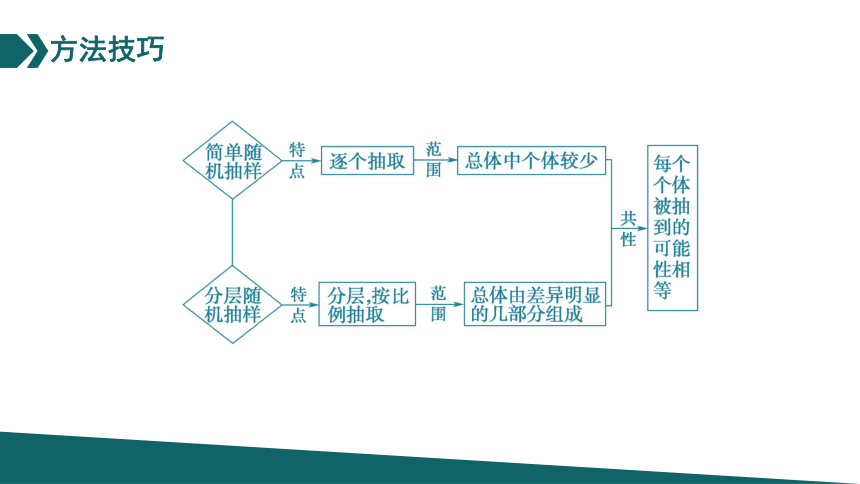
方法技巧
对比训练
1.某学校有教师200人,男学生1 200人,女学生1 000人.现用分层随机抽样的方法从全体师生中抽取一个容量为n的样本,若女学生一共抽取了80人,则n的值为( )
A.193 B.192 C.191 D.190
B
题型二 频率分布直方图及应用
【例2】 某花木公司为了调查某种树苗的生长情况,抽取了一个容量为100的样本,测得树苗的高度(cm)数据的分组及相应频数如下:
[107,109),3株;[109,111), 9株;[111,113),13株;
[113,115),16株;[115,117),26株;[117,119),20株;
[119,121),7株;[121,123),4株;[123,125],2株.
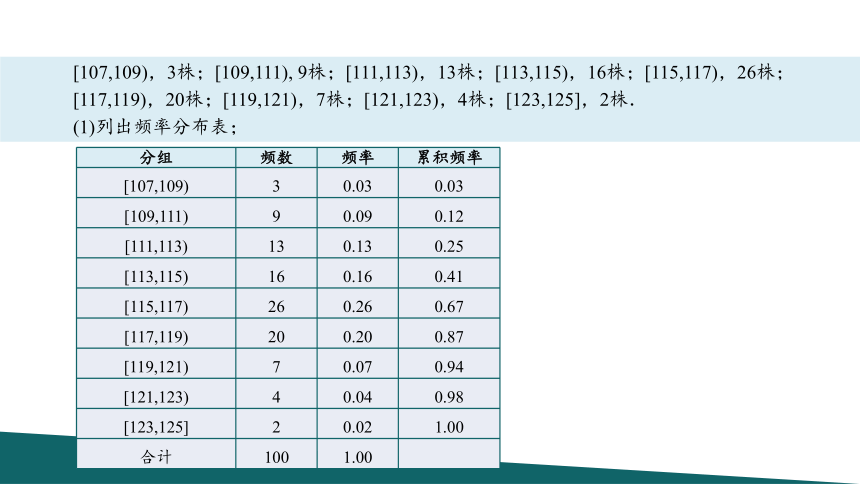
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)据上述图表,估计数据在[109,121)范围内的可能性是百分之几?
[107,109),3株;[109,111), 9株;[111,113),13株;[113,115),16株;[115,117),26株;[117,119),20株;[119,121),7株;[121,123),4株;[123,125],2株.
(1)列出频率分布表;
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
(2)画出频率分布直方图;
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
(3)据上述图表,估计数据在[109,121)范围内的可能性是百分之几?
由上述图表可知数据落在[109,121)范围内的频率为:0.94-0.03=0.91,
即数据落在[109,121)范围内的可能性是91%.
对比训练
2. 在本例中由得到的频率分布直方图估计树苗的高度(cm)的平均数.
由频率分布直方图可得树苗的高度(cm)的平均数的估计值为
0.03×108+0.09×110+0.13×112+0.16×114+0.26×116+0.20×118+0.07×120+0.04×122+0.02×124=115.46(cm)
方法技巧
(1)用样本频率分布估计总体频率分布时,通常要对给定的一组数据进行列表、作图处理,作频率分布表与频率分布直方图时要注意其方法步骤.
(2)借助图表,可以把抽样获得的庞杂数据变得直观,凸显其中的规律,便于信息的提取和交流.
用样本估计总体分布的方法
题型三 数据的集中趋势和离散程度的估计
【例3】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)求甲成绩的80%分位数;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由?
【例3】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)求甲成绩的80%分位数;
把甲的成绩按照从小到大的顺序排列可得:
78 79 81 82 84 88 93 95
因为一共有8个数据,所以8×80%=6.4,不是整数,
所以甲成绩的80%分位数是第7个数据93.
【例3】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由?
= [(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5
甲= (78+79+81+82+84+88+93+95)=85
乙= (75+80+80+83+85+90+92+95)=85
= [(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41
∵ 甲= 乙, < ,∴甲的成绩较稳定,派甲参赛比较合适.
方法技巧
用样本的数字特征估计总体的方法
为了从整体上更好地把握总体的规律,我们还可以通过样本数据的众数、中位数、平均数和标准差等数字特征对总体相应的数字特征作出估计.
众数就是样本数据中出现次数最多的那个值;
中位数就是把样本数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,处于中间位置的数,如果数据的个数是偶数,中间两个的数据的平均数;
平均数就是所有样本数据的平均值,用表示;
标准差是反映样本数据离散程度大小的最常用统计量.有时也用标准差的平方来代表标准差.
对比训练
3.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )
A.3 B. C.3 D.
分数 5 4 3 2 1
人数 20 10 30 30 10
B
统 计
知识体系
题型一 随机抽样方法的应用
专题复习
【例1】 某政府机关有在编人员100人,其中副处级以上干部10人,一般干部70人,干事20人,上级机关为了了解机关人员对政府机构的改革意见,要从中抽取一个容量为20的样本,试确定用何种方法抽取,如何抽取?
即从副处级以上干部中抽取2人,一般干部中抽取14人,干事中抽取4人.
用分层随机抽样抽取.
∵20∶100=1∶5,∴ =2, =14, =4,
∵副处级以上干部与干事人数都较少,他们分别按1~10编号和1~20编号,然后采用抽签法分别抽取2人和4人,对一般干部采用00,01,…,69编号,然后用随机数法抽取14人.
方法技巧
对比训练
1.某学校有教师200人,男学生1 200人,女学生1 000人.现用分层随机抽样的方法从全体师生中抽取一个容量为n的样本,若女学生一共抽取了80人,则n的值为( )
A.193 B.192 C.191 D.190
B
题型二 频率分布直方图及应用
【例2】 某花木公司为了调查某种树苗的生长情况,抽取了一个容量为100的样本,测得树苗的高度(cm)数据的分组及相应频数如下:
[107,109),3株;[109,111), 9株;[111,113),13株;
[113,115),16株;[115,117),26株;[117,119),20株;
[119,121),7株;[121,123),4株;[123,125],2株.
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)据上述图表,估计数据在[109,121)范围内的可能性是百分之几?
[107,109),3株;[109,111), 9株;[111,113),13株;[113,115),16株;[115,117),26株;[117,119),20株;[119,121),7株;[121,123),4株;[123,125],2株.
(1)列出频率分布表;
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
(2)画出频率分布直方图;
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
(3)据上述图表,估计数据在[109,121)范围内的可能性是百分之几?
由上述图表可知数据落在[109,121)范围内的频率为:0.94-0.03=0.91,
即数据落在[109,121)范围内的可能性是91%.
对比训练
2. 在本例中由得到的频率分布直方图估计树苗的高度(cm)的平均数.
由频率分布直方图可得树苗的高度(cm)的平均数的估计值为
0.03×108+0.09×110+0.13×112+0.16×114+0.26×116+0.20×118+0.07×120+0.04×122+0.02×124=115.46(cm)
方法技巧
(1)用样本频率分布估计总体频率分布时,通常要对给定的一组数据进行列表、作图处理,作频率分布表与频率分布直方图时要注意其方法步骤.
(2)借助图表,可以把抽样获得的庞杂数据变得直观,凸显其中的规律,便于信息的提取和交流.
用样本估计总体分布的方法
题型三 数据的集中趋势和离散程度的估计
【例3】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)求甲成绩的80%分位数;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由?
【例3】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)求甲成绩的80%分位数;
把甲的成绩按照从小到大的顺序排列可得:
78 79 81 82 84 88 93 95
因为一共有8个数据,所以8×80%=6.4,不是整数,
所以甲成绩的80%分位数是第7个数据93.
【例3】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由?
= [(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5
甲= (78+79+81+82+84+88+93+95)=85
乙= (75+80+80+83+85+90+92+95)=85
= [(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41
∵ 甲= 乙, < ,∴甲的成绩较稳定,派甲参赛比较合适.
方法技巧
用样本的数字特征估计总体的方法
为了从整体上更好地把握总体的规律,我们还可以通过样本数据的众数、中位数、平均数和标准差等数字特征对总体相应的数字特征作出估计.
众数就是样本数据中出现次数最多的那个值;
中位数就是把样本数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,处于中间位置的数,如果数据的个数是偶数,中间两个的数据的平均数;
平均数就是所有样本数据的平均值,用表示;
标准差是反映样本数据离散程度大小的最常用统计量.有时也用标准差的平方来代表标准差.
对比训练
3.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )
A.3 B. C.3 D.
分数 5 4 3 2 1
人数 20 10 30 30 10
B
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
