数学人教A版(2019)必修第一册2.2基本不等式 课件(共34张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册2.2基本不等式 课件(共34张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 624.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 11:17:15 | ||
图片预览










文档简介
(共34张PPT)
基本不等式
均值/
基本不等式:
注意:
当
时,基本不等式仍成立。
(2)在使用基本不等式时,一定要指出等号成立时的情况。
重要不等式:
注意:
(2)在使用基本不等式时,一定要指出等号成立时的情况。
(1)重要不等式对于任何实数都成立。
重要不等式与基本不等式的区别和联系
重要不等式 基本不等式
区别 适用范围
文字描述
等号成立的条件
联系
1构建基本不等式
重要不等式与基本不等式的区别和联系
重要不等式 基本不等式
区别 适用范围 任意两个实数 两个正数
文字描述 两个实数的平方和不小于它们乘积的两倍 两个正数的算术平均数不小于它们的几何平均数
等号成立的条件
联系 重要不等式通过字母代换可以得到基本不等式,而基本不等式通过不等式的性质也可以得到重要不等式
1构建基本不等式
作差法
2基本不等式的证明
——通过运算得出一个明显大于0的数
分析法
2基本不等式的证明
执果所因
从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显的成立条件(已知条件、定理、定义等)为止
要证 ①
只要证 ②
要证明②只要证 ③
要证明③只要证 ④
要证明④只要证 ⑤
要证明⑤只要证 ⑥
要证明⑥只要证 ⑦
显然⑦成立的,当且仅当a=b时,⑦中等号成立
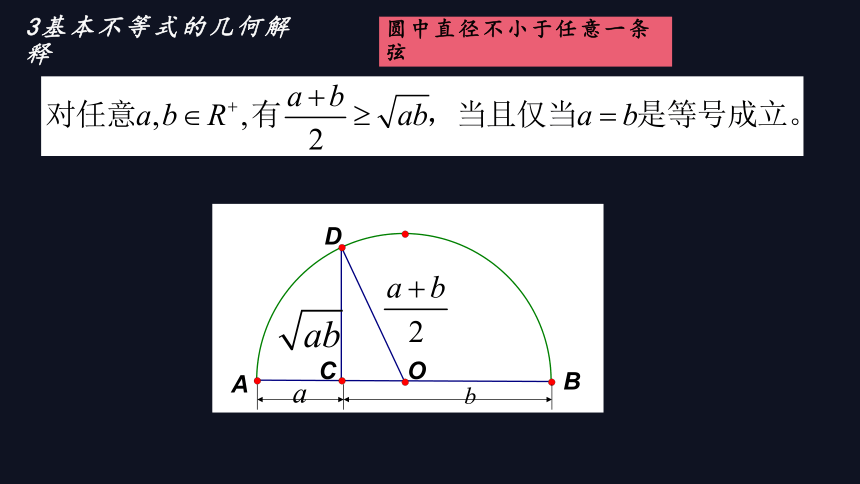
圆中直径不小于任意一条弦
3基本不等式的几何解释
运算形态的变式
不等式的性质 文字语言 基本不等式变式
自身对称性
同向同正可乘性
同向同正可除性
同向可加性
正数可乘方性
正数取倒
4基本不等式变形
换元拓展
换元方式 基本不等式变式
换字母
4基本不等式变形
倒数/调和平均数:数值倒数的平均数的倒数
第二课时
注意一下承上启下
分析
5基本不等式的应用
求代数式的最值
解:
分析
5基本不等式的应用
求代数式的最值
解:
求代数式的最值
5基本不等式的应用
两个的正数 的积为定值时它们的和有最小值
两个正数 的和为定值时它们的积有最大值
求代数式最值的数学模型
5基本不等式的应用
一正、二定、三相等
积定和最小和定积最大
求代数式的最值
5基本不等式的应用
积定和最小
和定积最大
①各项皆为正数;
②和或积为定值;
③注意等号成立的条件.
利用基本不等式求最值时,要注意条件
一“正”
二“定”
三“相等”
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
方法技巧
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
方法技巧
不定,应凑出定和或定积;
巩固练习
求代数式的最值
5基本不等式的应用
两个正数的积为定值时它们的和有最小值
和定积最大
两个正数的和为定值时它们的积有最大值
换元拓展
换元方式 基本不等式变式
换字母
2基本不等式变形
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
基本不等式
均值/
基本不等式:
注意:
当
时,基本不等式仍成立。
(2)在使用基本不等式时,一定要指出等号成立时的情况。
重要不等式:
注意:
(2)在使用基本不等式时,一定要指出等号成立时的情况。
(1)重要不等式对于任何实数都成立。
重要不等式与基本不等式的区别和联系
重要不等式 基本不等式
区别 适用范围
文字描述
等号成立的条件
联系
1构建基本不等式
重要不等式与基本不等式的区别和联系
重要不等式 基本不等式
区别 适用范围 任意两个实数 两个正数
文字描述 两个实数的平方和不小于它们乘积的两倍 两个正数的算术平均数不小于它们的几何平均数
等号成立的条件
联系 重要不等式通过字母代换可以得到基本不等式,而基本不等式通过不等式的性质也可以得到重要不等式
1构建基本不等式
作差法
2基本不等式的证明
——通过运算得出一个明显大于0的数
分析法
2基本不等式的证明
执果所因
从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显的成立条件(已知条件、定理、定义等)为止
要证 ①
只要证 ②
要证明②只要证 ③
要证明③只要证 ④
要证明④只要证 ⑤
要证明⑤只要证 ⑥
要证明⑥只要证 ⑦
显然⑦成立的,当且仅当a=b时,⑦中等号成立
圆中直径不小于任意一条弦
3基本不等式的几何解释
运算形态的变式
不等式的性质 文字语言 基本不等式变式
自身对称性
同向同正可乘性
同向同正可除性
同向可加性
正数可乘方性
正数取倒
4基本不等式变形
换元拓展
换元方式 基本不等式变式
换字母
4基本不等式变形
倒数/调和平均数:数值倒数的平均数的倒数
第二课时
注意一下承上启下
分析
5基本不等式的应用
求代数式的最值
解:
分析
5基本不等式的应用
求代数式的最值
解:
求代数式的最值
5基本不等式的应用
两个的正数 的积为定值时它们的和有最小值
两个正数 的和为定值时它们的积有最大值
求代数式最值的数学模型
5基本不等式的应用
一正、二定、三相等
积定和最小和定积最大
求代数式的最值
5基本不等式的应用
积定和最小
和定积最大
①各项皆为正数;
②和或积为定值;
③注意等号成立的条件.
利用基本不等式求最值时,要注意条件
一“正”
二“定”
三“相等”
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
方法技巧
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
方法技巧
不定,应凑出定和或定积;
巩固练习
求代数式的最值
5基本不等式的应用
两个正数的积为定值时它们的和有最小值
和定积最大
两个正数的和为定值时它们的积有最大值
换元拓展
换元方式 基本不等式变式
换字母
2基本不等式变形
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
利用基本不等式求最值
学透活用
一“正”二“定”三“相等”
积定和最小;和定积最大
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
