2022-2023学年人教版七年级数学上册第四章几何图形初步单元测试卷(A卷)(含答案解析)
文档属性
| 名称 | 2022-2023学年人教版七年级数学上册第四章几何图形初步单元测试卷(A卷)(含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 121.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 10:53:16 | ||
图片预览




文档简介
人教版七年级数学上册第四章《几何图形初步》单元测试卷(A)
一、单选题(本题共10小题,每小题5分,共50分)
1.某街道分布示意图如图所示,一个居民从A处前往B处,若规定只能走从左到右或从上到下的方向,这样该居民共有可选择的不同路线条数是( )
A.5 B.6 C.7 D.8
2.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
A.2cm B.4cm C.1cm D.6cm
3.如果一个角是50°,那么它的余角的度数是( )
A.40° B.50° C.100° D.130°
4.用一个平面去截一个正方体,截出截面不可能是( )
A.三角形 B.五边形 C.六边形 D.七边形
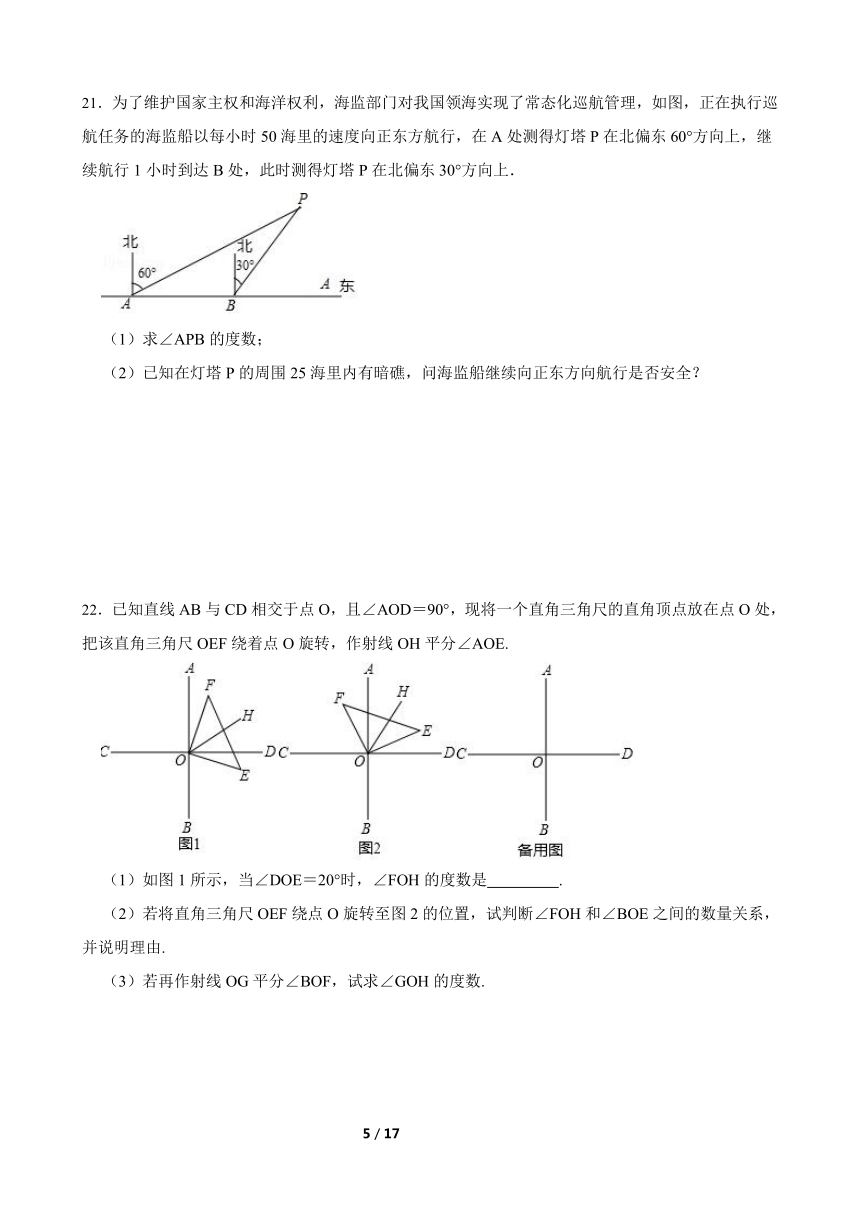
5.平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,若平面上不同的n个点最多可确定28条直线,则n的值是( )
A.6 B.7 C.8 D.9
6.如图, 与 互余, 与 互补, 平分 ,则 的度数是( )
A. B.
C. D.
7.如图所示,BO,CO分别是∠ABC,∠ACB的两条角平分线,∠A=100°,则∠BOC的度数为( ).
A.80° B.90° C.120° D.140°
8.将一张边长为30㎝的正方形纸片的四角分别剪去一个边长为x cm的小正方形,然后折叠成一个无盖的长方体.当x取下面哪个数值时,长方体的体积最大( )
A.7 B.6 C.5 D.4
9.如图,已知A,B(B在A的左侧)是数轴上的两点,点A对应的数为4,且,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左运动,在点P的运动过程中,M,N始终为AP,BP的中点,设运动时间为秒,则下列结论中正确的有( )
①B对应的数是2;②点P到达点B时,;③时,;④在点P的运动过程中,线段MN的长度不变.
A.①③④ B.②③④ C.②③ D.②④
10.已知,∠α与∠β互补,且∠α﹣∠β=30°,则∠α与∠β的大小关系依次为( )
A.110°,70° B.105°,75° C.100°,70° D.110°,80°
二、填空题(本题共5小题,每小题5分,共25分)
11.小朋友在用玩具枪瞄准时,总是用一只眼对准准星和目标,用数学知识解释为
12.如图所示,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数互为相反数,则x+y= .
第12题图 第15题图
13.平面内有公共端点的三条射线OA,OB,OC,构成的角 , ,OM和ON分别是 和 的角平分线,则 的度数是 .
14.线段 的长度为 ,点 为直线 上一点,且 ,点 为 的中点,则线段 的长度为 .
15.如图,已知点 是射线 上一点,过 作 交射线 于点 , 交射线 于点 ,给出下列结论:① 是 的余角;②图中互余的角共有3对;③ 的补角只有 ;④与 互补的角共有3个,其中正确结论有 (把你认为正确的结论的序号都填上).
三、解答题(本题共2小题,共15分)
16(8分).如图,已知C是AB的中点,D是AC的中点,E是BC的中点.
(1)若AB=18
cm,求DE的长;
(2)若CE=5 cm,求BD的长.
17(7分).如图,直线AB、CD相交于点O,OF⊥CD,OF平分∠BOE,垂足为O.
(1)直接写出图中所有与∠BOC互补的角;
(2)若∠BOE=110°,求∠AOC的度数.
四、综合题(本题共5小题,每小题12分,共60分)
18.如图,已知在数轴上有三个点 、 、 , 是原点,满足 , , ,动点 从点 出发向右以每秒 的速度匀速运动;同时,动点 从点 出发,在数轴上向左运动.
(1)若点 的速度为每秒 ,求 , 相遇时,运动的时间.
(2)若 的运动速度为每秒 时,经过多长时间 , 两点相距 ?
(3)当 时,点 运动的位置恰好是线段 的三等分点,求 的速度.
19.如下图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中 )A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交 于点P,则点P为水泵站的位置。
(1)你认为甲的建议符合要求吗?(管道总长最短)
(2)若认为合理,请说明理由,若不认同,那么你认为水泵站应该建在哪里?请在图中标出来,并说明作图的依据.
20.定义:从一个角的顶点出发,把这个角分成1∶2的两个角的射线,叫作这个角的三分线,显然,一个角的三分线有两条.例如:如图①,若∠BOC=2∠AOC,则OC是∠AOB的一条三分线.
(1)已知:如图①,OC是∠AOB的一条三分线,且∠BOC>∠AOC,若∠AOB=60°,求∠AOC的度数;
(2)已知:∠AOB=90°,如图②,若OC,OD是∠AOB的两条三分线.
①求∠COD的度数;
②现以O为中心,将∠COD顺时针旋转n度得到∠C′OD′,当OA恰好是∠C′OD′的三分线时,求n的值.
21.为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)求∠APB的度数;
(2)已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
22.已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.
(1)如图1所示,当∠DOE=20°时,∠FOH的度数是 .
(2)若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.
(3)若再作射线OG平分∠BOF,试求∠GOH的度数.
参考答案
一、单选题(本题共10小题,每小题5分,共50分)
1.【答案】D
【解析】如图,
可选择的不同路线条数有:
A→C→D→G→H→B;A→C→D→G→N→B;
A→C→F→G→H→B;A→C→F→G→N→B;
A→C→F→M→N→B;A→E→F→G→H→B;
A→E→F→G→N→B;A→E→F→M→N→B,共有8条不同
路线.
故选:D.
2.【答案】B
【解析】解:∵点M是AC的中点,点N是BC的中点,
∴AC=2MC,BC=2NC,
∴AC﹣BC=(MC﹣NC)×2=2×2=4(cm),
即AC比BC长4cm.
故选:B.
3.【答案】A
【解析】【解答】解:∵一个角是50°,
∴它的余角的度数是:90°﹣50°=40°,
故选:A.
4.【答案】D
【解析】【解答】解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此不可能是七边形.
故选:D.
5.【答案】C
【解析】【解答】解:两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线,
因为1+2+3+4+5+6+7=28,
所以平面上不同的8个点最多可确定28条直线.
故选C.
6.【答案】B
【解析】解:∵∠AOB与∠AOC互余,∠AOD与∠AOC互补,
∴∠AOB=90°-∠AOC,∠AOD=180°-∠AOC,
∴∠BOD=∠AOD-∠AOB=90°,
∵OC平分∠BOD,
∴∠BOC=45°,
∴∠AOC=45°+∠AOB,
∴∠AOB=90°-∠AOC=90°-(45°+∠AOB),
∴∠AOB=22.5°,
故答案为:B.
7.【答案】D
【解析】△ABC中,∠ABC+∠ACB=180°-∠A=180°-100°=80°,
∵BO、CO是∠ABC,∠ACB的两条角平分线.
∴∠OBC= ∠ABC,∠OCB= ∠ACB,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=40°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=140°.
故答案为:D.
8.【答案】C
【解析】长方体体积=(30-2x)2 x,
将x=7代入得:体积为(30-14)2×7=1792;
将x=6代入得:体积为(30-12)2×6=1944;
将x=5代入得:体积为(30-10)2×5=2000;
将x=4代入得:体积为(30-8)2×4=1936,
则x=5时,体积最大.
故选C.
9.【答案】D
【解析】【解答】解:设点B对应的数是x,
∵点A对应的数为4,且 ,
∴ ,
∴ ,
∴点B对应的数是-2,故①不符合题意;
由题意得:
6÷2=3(秒),
∴点P到达点B时,t=3,故②符合题意;
分两种情况:
当点P在点B的右侧,
∵AB=6,BP=2,
∴,
∴4÷2=2(秒),
∴BP=2时,t=2,
当点P在点B的左侧,
∵AB=6,BP=2,
∴,
∴8÷2=4(秒),
∴BP=2时,t=4,
综上所述,BP=2时,t=2或4,故③不符合题意;
分两种情况:
当点P在点B的右侧,
∵M,N分别为AP,BP的中点,
∴,,
∴,
当点P在点B的左侧,
∵M,N分别为AP,BP的中点,
,,
∴,
∴在点P的运动过程中,线段MN的长度不变,故④符合题意.
所以,上列结论中正确的是②④.
故答案为:D.
10.【答案】B
【解析】解:∵∠α与∠β互为补角,
∴∠α+∠β=180°,
又∵∠α﹣∠β=30°,
∴ ,
解得: ,
故选B.
二、填空题(本题共5小题,每小题5分,共25分)
11.【答案】两点确定一条直线
【解析】解:∵准星与目标是两点,
∴利用的数学知识是:两点确定一条直线.
故答案是:两点确定一条直线
12.【答案】-6
【解析】将题图中平面展开图按虚线折叠成正方体后,可知标有数字“2”的面和标有x的面是相对面,标有数字“4”的面和标有y的面是相对面.
∵相对面上两个数互为相反数,∴x=-2,y=-4,∴x+y=-6.
故答案为:-6.
13.【答案】20°或50°
【解析】【解答】分两种情况讨论,
①如图,
OM和ON分别是 和 的角平分线,
,
,
②如图,
OM和ON分别是 和 的角平分线,
,
,
综上所述, 的度数是20°或50°,
故答案为:20°或50°.
14.【答案】9cm或11cm
【解析】解:∵AB=10cm, ,
∴BC=2cm,
∵点E为BC的中点,
∴ ,
∴①当点C在线段AB上,如图所示:
则有:AE=AB-BE=9cm,
②当点C在线段AB的延长线上,如图所示:
则有:AE=AB+BE=11cm,
综上所述:线段AE的长度为9cm或11cm;
故答案为:9cm或11cm.
15.【答案】①④
【解析】解: CA⊥BE ,
∠1是∠B的余角,故①符合题意;
,
∴ ∠1与∠CAD互为余角,∠B与∠BAD互为余角,
CA⊥BE ,
∴ ∠CAD与∠BAD互为余角,
所以图中互余的角共有4对,故②不符合题意;
∠1与∠ACF互补;
∵∠1+∠DAC=90°,∠BAD+∠DAC=90°,
∴∠1=∠BAD,
∵∠BAD+∠DAE=180°,
∴∠1+∠DAE=180°,
∴∠1与∠DAE互补, 故③不符合题意;
CA⊥BE ,AD⊥BF
所以与∠ADB互补的角有∠ADC、∠CAB、∠CAE共3个,故④符合题意;
所以正确的结论有:①④
故答案为:①④.
三、计算题(本题共2小题,,共15分)
16.【答案】(1)9cm (2)15cm
【解析】【解答】解(1)∵C是AB的中点,AB=18cm,
∴AC=BC=AB=9cm,
∵D是AC的中点,E是BC的中点.
∴CD=AC=4.5cm,CE=BC=4.5cm,
∴DE=CD+CE=9cm.
(2)由(1)知,AD=CD=CE=BE,
∴CE=BD,
∵CE=5cm,
∴BD=15cm,
17.【答案】(1)解:∵∠AOC+∠BOC=180°,∠BOD+∠BOC=180°,
∴∠AOC和∠BOD与∠BOC互补;
∵OF⊥CD,
∴∠COF=∠DOF=90°,
∴∠COE+∠EOF=∠DOB+∠BOF=90°,
∵OF平分∠BOE,
∴∠BOF=∠EOF,
∴∠COE=∠BOD,
∴∠COE+∠BOC=180°,
∴图中所有与∠BOC互补的角有∠AOC,∠BOD,∠COE
(2)解:∵∠BOE=110°,OF平分∠BOE,
∴∠BOF= ∠BOE=55°,
∵OF⊥CD,
∴∠DOF=90°,
∴∠DOB=35°,
∴∠AOC=∠BOD=35°
【解析】(1)根据补角的定义即可得到结论;(2)根据角平分线的定义得到∠BOF= ∠BOE=55°,根据余角的定义和对顶角的性质即可得到结论.
四、解答题(本题共5小题,每小题12分,共60分)
18【答案】(1)解:设 、 相遇时,运动的时间为 ,
由题知: ,
∴当 、 相遇时, ,即 .
∴解得: ,故 、 相遇时的运动时间为 .
(2)解:∵ ,
∴分两种情况,
① 在 的右侧时,经过时间为 ,
② 在 的左侧时,设经过时间 , 、 两点相距 ,
此时 , ,∴ ,
解得: ,
综合①②得知,经过5秒和40秒时 、 两点相距 .
(3)解: ,分两种情况,
①当点 在 、 两点之间时,
∵ ,
∴ ,
此时运动的时间为
∵点 运动的位置恰好是线段 的三等分,
∴ 或 ,
点 的运动速度为 或 ;
②当点 在线段 的延长线上时,
∵ ,
∴ ,
此时运动的时间为 ,
∵点 运动的位置恰好是线段 的三等分,
∴ 或 ,
点 的运动速度为 或 ;
综合①②得知,当点 在 、 两点之间时,点 的运动速度为 或 ;
当点 在线段 的延长线上时,点 的运动速度为 或 .
【解析】(1)设、相遇时,运动的时间为,可得OP=t,CQ=0.8t,根据OP+CQ=OC列出方程,求出t值即可;
(2) 由于① 在 的右侧时,② 在 的左侧时,据此分别求出结论即可;
(3) ,分两种情况,①当点 在 、 两点之间时, ②当点 在线段 的延长线上时,据此分别解答即可.
19.【答案】(1)解:不符合要求
(2)解:连接AB,交m于点Q,水泵站应建在Q处。图略,
依据是:两点之间线段最短
【解析】(1)根据两点之间线段最短,点P的位置不符合要求;(2)根据两点之间线段最短,连接AB与m的交点即为所求.
【答案】(1)解:∵OC是∠AOB的一条三分线,且∠BOC>∠AOC,
∴∠AOC= ∠AOB= ×60°=20°
(2)解:①∵∠AOB=90°,OC,OD是∠AOB的两条三分线,
∴∠BOC=∠AOD= ∠AOB= ×90°=30°,
∴∠COD=∠AOB-∠BOC-∠AOD=90°-30°-30°=30°.
②分两种情况:当OA是∠C′OD′的三分线,且∠AOD′>∠AOC′时,如图①,
∠AOC′= ∠C′OD′=10°,
∴∠DOC′=∠AOD-∠AOC′=30°-10°=20°,
∴∠DOD′=∠DOC′+∠C′OD′=20°+30°=50°;
当OA是∠C′OD′的三分线,且∠AOD′<∠AOC′时,如图②,
∠AOC′=20°,
∴∠DOC′=∠AOD-∠AOC′=30°-20°=10°,
∴∠DOD′=∠DOC′+∠C′OD′=10°+30°=40°.
综上所述,n=40或50.
【解析】(1)根据OC是∠AOB的一条三分线,计算出∠AOC的度数。
(2)根据OC、OD是∠AOB的两条三分线,求出∠COD的度数;当OA是∠C′OD′的三分线,考虑∠AOD′<∠AOC′和∠AOD′>∠AOC′的情况。
21.【答案】(1)解:在△APB中,∠PAB=30°,∠ABP=120°
∴∠APB=180°-30°-120°=30°;
(2)解:过点P作PH⊥AB于点H
在Rt△APH中,∠PAH=30°,AH= PH
在Rt△BPH中,∠PBH=30°,BH= PH
∴AB=AH-BH= PH=50
算出PH=25 >25,不会进入暗礁区,继续航行仍然安全.
【解析】(1)根据题意得到△APB其余两个角的度数,从而利用三角形内角和定理即可求得∠APB;(2)只需算出航线上与P点最近距离为多少即可.
22.【答案】(1)35° (2)∠BOE=2∠FOH (3)∠GOH的度数为45° 或135°.
解:(1)因为∠AOD=90° ,∠DOE=20°
所以∠AOE=∠AOD+∠DOE=110°
因为OH平分∠AOE
所以∠HOE= AOE=55°
所以∠FOH=90° ﹣∠HOE=35° ;
故答案为:35 ° ;
(2)∠BOE=2∠FOH,理由如下:
设∠AOH=x,
因为OH平分∠AOE
所以∠HOE=∠AOH=x
所以∠FOH=90 °﹣∠HOE=90°﹣x
∠BOE=180°﹣∠AOE=180°﹣2x
所以∠BOE=2∠FOH;
(3)解:如图3,当OE落在∠BOD内时,OF落在∠AOD内
因为OH平分∠AOE
所以∠HOE=∠AOH= AOE
因为OG平分∠BOF
∠FOG=∠GOB= BOF
所以∠GOH=∠GOF﹣∠FOH
= BOF﹣(∠AOH﹣∠AOF)
= (180°﹣∠AOF)﹣ AOE+∠AOF
=90°﹣ AOF﹣ (90°+∠AOF)+∠AOF
=90°﹣ AOF﹣45°﹣ AOF+∠AOF
=45°;
所以∠GOH的度数为45°;
如图4,当OE落在其他位置时
因为OH平分∠AOE
所以∠HOE=∠AOH= AOE
因为OG平分∠BOF
∠FOG=∠GOB= BOF
所以∠GOH=∠GOF+∠FOH
= BOF+∠AOH+∠AOF
= (180°﹣∠AOF)+ AOE+∠AOF
=90°﹣ AOF+ (90°﹣∠AOF)+∠AOF
=90°﹣ AOF+45°﹣ AOF+∠AOF
=135°;
所以∠GOH的度数为135°
综上所述:∠GOH的度数为45° 或135°.
1 / 1
一、单选题(本题共10小题,每小题5分,共50分)
1.某街道分布示意图如图所示,一个居民从A处前往B处,若规定只能走从左到右或从上到下的方向,这样该居民共有可选择的不同路线条数是( )
A.5 B.6 C.7 D.8
2.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
A.2cm B.4cm C.1cm D.6cm
3.如果一个角是50°,那么它的余角的度数是( )
A.40° B.50° C.100° D.130°
4.用一个平面去截一个正方体,截出截面不可能是( )
A.三角形 B.五边形 C.六边形 D.七边形
5.平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,若平面上不同的n个点最多可确定28条直线,则n的值是( )
A.6 B.7 C.8 D.9
6.如图, 与 互余, 与 互补, 平分 ,则 的度数是( )
A. B.
C. D.
7.如图所示,BO,CO分别是∠ABC,∠ACB的两条角平分线,∠A=100°,则∠BOC的度数为( ).
A.80° B.90° C.120° D.140°
8.将一张边长为30㎝的正方形纸片的四角分别剪去一个边长为x cm的小正方形,然后折叠成一个无盖的长方体.当x取下面哪个数值时,长方体的体积最大( )
A.7 B.6 C.5 D.4
9.如图,已知A,B(B在A的左侧)是数轴上的两点,点A对应的数为4,且,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左运动,在点P的运动过程中,M,N始终为AP,BP的中点,设运动时间为秒,则下列结论中正确的有( )
①B对应的数是2;②点P到达点B时,;③时,;④在点P的运动过程中,线段MN的长度不变.
A.①③④ B.②③④ C.②③ D.②④
10.已知,∠α与∠β互补,且∠α﹣∠β=30°,则∠α与∠β的大小关系依次为( )
A.110°,70° B.105°,75° C.100°,70° D.110°,80°
二、填空题(本题共5小题,每小题5分,共25分)
11.小朋友在用玩具枪瞄准时,总是用一只眼对准准星和目标,用数学知识解释为
12.如图所示,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数互为相反数,则x+y= .
第12题图 第15题图
13.平面内有公共端点的三条射线OA,OB,OC,构成的角 , ,OM和ON分别是 和 的角平分线,则 的度数是 .
14.线段 的长度为 ,点 为直线 上一点,且 ,点 为 的中点,则线段 的长度为 .
15.如图,已知点 是射线 上一点,过 作 交射线 于点 , 交射线 于点 ,给出下列结论:① 是 的余角;②图中互余的角共有3对;③ 的补角只有 ;④与 互补的角共有3个,其中正确结论有 (把你认为正确的结论的序号都填上).
三、解答题(本题共2小题,共15分)
16(8分).如图,已知C是AB的中点,D是AC的中点,E是BC的中点.
(1)若AB=18
cm,求DE的长;
(2)若CE=5 cm,求BD的长.
17(7分).如图,直线AB、CD相交于点O,OF⊥CD,OF平分∠BOE,垂足为O.
(1)直接写出图中所有与∠BOC互补的角;
(2)若∠BOE=110°,求∠AOC的度数.
四、综合题(本题共5小题,每小题12分,共60分)
18.如图,已知在数轴上有三个点 、 、 , 是原点,满足 , , ,动点 从点 出发向右以每秒 的速度匀速运动;同时,动点 从点 出发,在数轴上向左运动.
(1)若点 的速度为每秒 ,求 , 相遇时,运动的时间.
(2)若 的运动速度为每秒 时,经过多长时间 , 两点相距 ?
(3)当 时,点 运动的位置恰好是线段 的三等分点,求 的速度.
19.如下图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中 )A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交 于点P,则点P为水泵站的位置。
(1)你认为甲的建议符合要求吗?(管道总长最短)
(2)若认为合理,请说明理由,若不认同,那么你认为水泵站应该建在哪里?请在图中标出来,并说明作图的依据.
20.定义:从一个角的顶点出发,把这个角分成1∶2的两个角的射线,叫作这个角的三分线,显然,一个角的三分线有两条.例如:如图①,若∠BOC=2∠AOC,则OC是∠AOB的一条三分线.
(1)已知:如图①,OC是∠AOB的一条三分线,且∠BOC>∠AOC,若∠AOB=60°,求∠AOC的度数;
(2)已知:∠AOB=90°,如图②,若OC,OD是∠AOB的两条三分线.
①求∠COD的度数;
②现以O为中心,将∠COD顺时针旋转n度得到∠C′OD′,当OA恰好是∠C′OD′的三分线时,求n的值.
21.为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)求∠APB的度数;
(2)已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
22.已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.
(1)如图1所示,当∠DOE=20°时,∠FOH的度数是 .
(2)若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.
(3)若再作射线OG平分∠BOF,试求∠GOH的度数.
参考答案
一、单选题(本题共10小题,每小题5分,共50分)
1.【答案】D
【解析】如图,
可选择的不同路线条数有:
A→C→D→G→H→B;A→C→D→G→N→B;
A→C→F→G→H→B;A→C→F→G→N→B;
A→C→F→M→N→B;A→E→F→G→H→B;
A→E→F→G→N→B;A→E→F→M→N→B,共有8条不同
路线.
故选:D.
2.【答案】B
【解析】解:∵点M是AC的中点,点N是BC的中点,
∴AC=2MC,BC=2NC,
∴AC﹣BC=(MC﹣NC)×2=2×2=4(cm),
即AC比BC长4cm.
故选:B.
3.【答案】A
【解析】【解答】解:∵一个角是50°,
∴它的余角的度数是:90°﹣50°=40°,
故选:A.
4.【答案】D
【解析】【解答】解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此不可能是七边形.
故选:D.
5.【答案】C
【解析】【解答】解:两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线,
因为1+2+3+4+5+6+7=28,
所以平面上不同的8个点最多可确定28条直线.
故选C.
6.【答案】B
【解析】解:∵∠AOB与∠AOC互余,∠AOD与∠AOC互补,
∴∠AOB=90°-∠AOC,∠AOD=180°-∠AOC,
∴∠BOD=∠AOD-∠AOB=90°,
∵OC平分∠BOD,
∴∠BOC=45°,
∴∠AOC=45°+∠AOB,
∴∠AOB=90°-∠AOC=90°-(45°+∠AOB),
∴∠AOB=22.5°,
故答案为:B.
7.【答案】D
【解析】△ABC中,∠ABC+∠ACB=180°-∠A=180°-100°=80°,
∵BO、CO是∠ABC,∠ACB的两条角平分线.
∴∠OBC= ∠ABC,∠OCB= ∠ACB,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=40°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=140°.
故答案为:D.
8.【答案】C
【解析】长方体体积=(30-2x)2 x,
将x=7代入得:体积为(30-14)2×7=1792;
将x=6代入得:体积为(30-12)2×6=1944;
将x=5代入得:体积为(30-10)2×5=2000;
将x=4代入得:体积为(30-8)2×4=1936,
则x=5时,体积最大.
故选C.
9.【答案】D
【解析】【解答】解:设点B对应的数是x,
∵点A对应的数为4,且 ,
∴ ,
∴ ,
∴点B对应的数是-2,故①不符合题意;
由题意得:
6÷2=3(秒),
∴点P到达点B时,t=3,故②符合题意;
分两种情况:
当点P在点B的右侧,
∵AB=6,BP=2,
∴,
∴4÷2=2(秒),
∴BP=2时,t=2,
当点P在点B的左侧,
∵AB=6,BP=2,
∴,
∴8÷2=4(秒),
∴BP=2时,t=4,
综上所述,BP=2时,t=2或4,故③不符合题意;
分两种情况:
当点P在点B的右侧,
∵M,N分别为AP,BP的中点,
∴,,
∴,
当点P在点B的左侧,
∵M,N分别为AP,BP的中点,
,,
∴,
∴在点P的运动过程中,线段MN的长度不变,故④符合题意.
所以,上列结论中正确的是②④.
故答案为:D.
10.【答案】B
【解析】解:∵∠α与∠β互为补角,
∴∠α+∠β=180°,
又∵∠α﹣∠β=30°,
∴ ,
解得: ,
故选B.
二、填空题(本题共5小题,每小题5分,共25分)
11.【答案】两点确定一条直线
【解析】解:∵准星与目标是两点,
∴利用的数学知识是:两点确定一条直线.
故答案是:两点确定一条直线
12.【答案】-6
【解析】将题图中平面展开图按虚线折叠成正方体后,可知标有数字“2”的面和标有x的面是相对面,标有数字“4”的面和标有y的面是相对面.
∵相对面上两个数互为相反数,∴x=-2,y=-4,∴x+y=-6.
故答案为:-6.
13.【答案】20°或50°
【解析】【解答】分两种情况讨论,
①如图,
OM和ON分别是 和 的角平分线,
,
,
②如图,
OM和ON分别是 和 的角平分线,
,
,
综上所述, 的度数是20°或50°,
故答案为:20°或50°.
14.【答案】9cm或11cm
【解析】解:∵AB=10cm, ,
∴BC=2cm,
∵点E为BC的中点,
∴ ,
∴①当点C在线段AB上,如图所示:
则有:AE=AB-BE=9cm,
②当点C在线段AB的延长线上,如图所示:
则有:AE=AB+BE=11cm,
综上所述:线段AE的长度为9cm或11cm;
故答案为:9cm或11cm.
15.【答案】①④
【解析】解: CA⊥BE ,
∠1是∠B的余角,故①符合题意;
,
∴ ∠1与∠CAD互为余角,∠B与∠BAD互为余角,
CA⊥BE ,
∴ ∠CAD与∠BAD互为余角,
所以图中互余的角共有4对,故②不符合题意;
∠1与∠ACF互补;
∵∠1+∠DAC=90°,∠BAD+∠DAC=90°,
∴∠1=∠BAD,
∵∠BAD+∠DAE=180°,
∴∠1+∠DAE=180°,
∴∠1与∠DAE互补, 故③不符合题意;
CA⊥BE ,AD⊥BF
所以与∠ADB互补的角有∠ADC、∠CAB、∠CAE共3个,故④符合题意;
所以正确的结论有:①④
故答案为:①④.
三、计算题(本题共2小题,,共15分)
16.【答案】(1)9cm (2)15cm
【解析】【解答】解(1)∵C是AB的中点,AB=18cm,
∴AC=BC=AB=9cm,
∵D是AC的中点,E是BC的中点.
∴CD=AC=4.5cm,CE=BC=4.5cm,
∴DE=CD+CE=9cm.
(2)由(1)知,AD=CD=CE=BE,
∴CE=BD,
∵CE=5cm,
∴BD=15cm,
17.【答案】(1)解:∵∠AOC+∠BOC=180°,∠BOD+∠BOC=180°,
∴∠AOC和∠BOD与∠BOC互补;
∵OF⊥CD,
∴∠COF=∠DOF=90°,
∴∠COE+∠EOF=∠DOB+∠BOF=90°,
∵OF平分∠BOE,
∴∠BOF=∠EOF,
∴∠COE=∠BOD,
∴∠COE+∠BOC=180°,
∴图中所有与∠BOC互补的角有∠AOC,∠BOD,∠COE
(2)解:∵∠BOE=110°,OF平分∠BOE,
∴∠BOF= ∠BOE=55°,
∵OF⊥CD,
∴∠DOF=90°,
∴∠DOB=35°,
∴∠AOC=∠BOD=35°
【解析】(1)根据补角的定义即可得到结论;(2)根据角平分线的定义得到∠BOF= ∠BOE=55°,根据余角的定义和对顶角的性质即可得到结论.
四、解答题(本题共5小题,每小题12分,共60分)
18【答案】(1)解:设 、 相遇时,运动的时间为 ,
由题知: ,
∴当 、 相遇时, ,即 .
∴解得: ,故 、 相遇时的运动时间为 .
(2)解:∵ ,
∴分两种情况,
① 在 的右侧时,经过时间为 ,
② 在 的左侧时,设经过时间 , 、 两点相距 ,
此时 , ,∴ ,
解得: ,
综合①②得知,经过5秒和40秒时 、 两点相距 .
(3)解: ,分两种情况,
①当点 在 、 两点之间时,
∵ ,
∴ ,
此时运动的时间为
∵点 运动的位置恰好是线段 的三等分,
∴ 或 ,
点 的运动速度为 或 ;
②当点 在线段 的延长线上时,
∵ ,
∴ ,
此时运动的时间为 ,
∵点 运动的位置恰好是线段 的三等分,
∴ 或 ,
点 的运动速度为 或 ;
综合①②得知,当点 在 、 两点之间时,点 的运动速度为 或 ;
当点 在线段 的延长线上时,点 的运动速度为 或 .
【解析】(1)设、相遇时,运动的时间为,可得OP=t,CQ=0.8t,根据OP+CQ=OC列出方程,求出t值即可;
(2) 由于① 在 的右侧时,② 在 的左侧时,据此分别求出结论即可;
(3) ,分两种情况,①当点 在 、 两点之间时, ②当点 在线段 的延长线上时,据此分别解答即可.
19.【答案】(1)解:不符合要求
(2)解:连接AB,交m于点Q,水泵站应建在Q处。图略,
依据是:两点之间线段最短
【解析】(1)根据两点之间线段最短,点P的位置不符合要求;(2)根据两点之间线段最短,连接AB与m的交点即为所求.
【答案】(1)解:∵OC是∠AOB的一条三分线,且∠BOC>∠AOC,
∴∠AOC= ∠AOB= ×60°=20°
(2)解:①∵∠AOB=90°,OC,OD是∠AOB的两条三分线,
∴∠BOC=∠AOD= ∠AOB= ×90°=30°,
∴∠COD=∠AOB-∠BOC-∠AOD=90°-30°-30°=30°.
②分两种情况:当OA是∠C′OD′的三分线,且∠AOD′>∠AOC′时,如图①,
∠AOC′= ∠C′OD′=10°,
∴∠DOC′=∠AOD-∠AOC′=30°-10°=20°,
∴∠DOD′=∠DOC′+∠C′OD′=20°+30°=50°;
当OA是∠C′OD′的三分线,且∠AOD′<∠AOC′时,如图②,
∠AOC′=20°,
∴∠DOC′=∠AOD-∠AOC′=30°-20°=10°,
∴∠DOD′=∠DOC′+∠C′OD′=10°+30°=40°.
综上所述,n=40或50.
【解析】(1)根据OC是∠AOB的一条三分线,计算出∠AOC的度数。
(2)根据OC、OD是∠AOB的两条三分线,求出∠COD的度数;当OA是∠C′OD′的三分线,考虑∠AOD′<∠AOC′和∠AOD′>∠AOC′的情况。
21.【答案】(1)解:在△APB中,∠PAB=30°,∠ABP=120°
∴∠APB=180°-30°-120°=30°;
(2)解:过点P作PH⊥AB于点H
在Rt△APH中,∠PAH=30°,AH= PH
在Rt△BPH中,∠PBH=30°,BH= PH
∴AB=AH-BH= PH=50
算出PH=25 >25,不会进入暗礁区,继续航行仍然安全.
【解析】(1)根据题意得到△APB其余两个角的度数,从而利用三角形内角和定理即可求得∠APB;(2)只需算出航线上与P点最近距离为多少即可.
22.【答案】(1)35° (2)∠BOE=2∠FOH (3)∠GOH的度数为45° 或135°.
解:(1)因为∠AOD=90° ,∠DOE=20°
所以∠AOE=∠AOD+∠DOE=110°
因为OH平分∠AOE
所以∠HOE= AOE=55°
所以∠FOH=90° ﹣∠HOE=35° ;
故答案为:35 ° ;
(2)∠BOE=2∠FOH,理由如下:
设∠AOH=x,
因为OH平分∠AOE
所以∠HOE=∠AOH=x
所以∠FOH=90 °﹣∠HOE=90°﹣x
∠BOE=180°﹣∠AOE=180°﹣2x
所以∠BOE=2∠FOH;
(3)解:如图3,当OE落在∠BOD内时,OF落在∠AOD内
因为OH平分∠AOE
所以∠HOE=∠AOH= AOE
因为OG平分∠BOF
∠FOG=∠GOB= BOF
所以∠GOH=∠GOF﹣∠FOH
= BOF﹣(∠AOH﹣∠AOF)
= (180°﹣∠AOF)﹣ AOE+∠AOF
=90°﹣ AOF﹣ (90°+∠AOF)+∠AOF
=90°﹣ AOF﹣45°﹣ AOF+∠AOF
=45°;
所以∠GOH的度数为45°;
如图4,当OE落在其他位置时
因为OH平分∠AOE
所以∠HOE=∠AOH= AOE
因为OG平分∠BOF
∠FOG=∠GOB= BOF
所以∠GOH=∠GOF+∠FOH
= BOF+∠AOH+∠AOF
= (180°﹣∠AOF)+ AOE+∠AOF
=90°﹣ AOF+ (90°﹣∠AOF)+∠AOF
=90°﹣ AOF+45°﹣ AOF+∠AOF
=135°;
所以∠GOH的度数为135°
综上所述:∠GOH的度数为45° 或135°.
1 / 1
