青岛版数学八年级上册 4.5方差第1课时 课件(共18张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 4.5方差第1课时 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 486.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第1课时
4.5 方 差
田径队的甲乙两名运动员在8次百米跑训练中,成绩如下表:教练想选择一名运动员参加比赛,该如何选择呢?
序数 1 2 3 4 5 6 7 8
甲的成绩/s 12.0 12.2 13.0 12.6 13.1 12.5 12.4 12.2
乙的成绩s 12.2 12.4 12.7 12.5 12.9 12.2 12.8 12.3
体育老师的烦恼?
教学目标:
1.了解方差的定义和计算公式。
2.理解方差概念的产生和形成的过程。
3.会用方差计算公式来比较两组数据的波动大小。
预习诊断
1.为了刻画一组数据的离散程度,通常选用____________________ 来描述。
2.方差越小,这组数据的离散程度就越 ,数据就越 ,平均数的代表性就越 。
3.方差的单位是原数据单位的 。
4.甲、乙两个样本中,则两个样本的波动情况是( )
A.甲的波动比乙大 B.乙的波动比甲大
C.甲、乙波动一样大 D.无法比较
5.有5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):2,-2,-1,1,0。则这组数据的方差为_____。
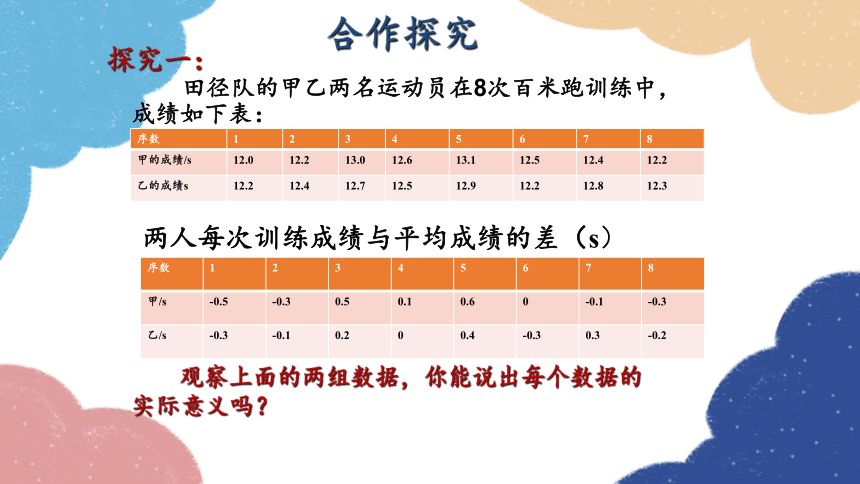
田径队的甲乙两名运动员在8次百米跑训练中,成绩如下表:
序数 1 2 3 4 5 6 7 8
甲的成绩/s 12.0 12.2 13.0 12.6 13.1 12.5 12.4 12.2
乙的成绩s 12.2 12.4 12.7 12.5 12.9 12.2 12.8 12.3
序数 1 2 3 4 5 6 7 8
甲/s -0.5 -0.3 0.5 0.1 0.6 0 -0.1 -0.3
乙/s -0.3 -0.1 0.2 0 0.4 -0.3 0.3 -0.2
两人每次训练成绩与平均成绩的差(s)
观察上面的两组数据,你能说出每个数据的实际意义吗?
合作探究
探究一:
离差:
在一组数据中,一个数据与这组数据的平均数的差。
离差可能是正数,可能是负数,也可能是0。
离差的符号和大小反映了该数据偏离平均数的程度。
探究二:
如何利用一组数据中全部数据的离差来反映这组数据的离散程度呢?
怎么办
方案一:
用所有数据的离差之和表示一组数据的离散程度。
甲:
乙:
这是不是偶然现象呢?
设 是数据为x1, x2, x3,……,xn的平均数,n为数据的个数,那么
方案二:
取一组数据中所有数据的离差的绝对值之和。
你同意这种方案吗?说说理由。
(改进的)方案:
离差的平方和的平均数(方差)
方差越大,说明数据的波动越大,越不稳定。
方差用来衡量一组数据的波动大小。(即这组数据偏离平均数的大小)。
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数。
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”。
归纳
(1)已知数据1,4,3,5,2,则这5个数的方差是____。
(2)绝对值小于 的所有整数的方差是______。
(3)一组数据:a, a, a, …,a(有n个a),则它的方差为___。
反馈练习
例:为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,
测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐?
思考:求数据方差的一般步骤是什么?
1.求数据的平均数;
2.利用方差公式求方差。
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
精讲点拨
在一次芭蕾舞的比赛中,甲,乙两个芭蕾舞团表演了舞剧《天鹅舞》,参加表演的女演员的身高(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞女演员的身高更整齐?
试一试
方差越大,说明数据的波动越大,越不稳定。
方差用来衡量一组数据的波动大小
(即这组数据偏离平均数的大小)。
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数。
课堂小结
探索发现
已知三组数据1,2,3,4,5;11,12,13,14,15
和3,6,9,12,15。
1.求这三组数据的平均数和方差。
2.对照以上结果,你能从中发现哪些有趣的结论?
平均数 方差
1,2,3,4,5
11,12,13,14,15
3,6,9,12,15
谢 谢
第1课时
4.5 方 差
田径队的甲乙两名运动员在8次百米跑训练中,成绩如下表:教练想选择一名运动员参加比赛,该如何选择呢?
序数 1 2 3 4 5 6 7 8
甲的成绩/s 12.0 12.2 13.0 12.6 13.1 12.5 12.4 12.2
乙的成绩s 12.2 12.4 12.7 12.5 12.9 12.2 12.8 12.3
体育老师的烦恼?
教学目标:
1.了解方差的定义和计算公式。
2.理解方差概念的产生和形成的过程。
3.会用方差计算公式来比较两组数据的波动大小。
预习诊断
1.为了刻画一组数据的离散程度,通常选用____________________ 来描述。
2.方差越小,这组数据的离散程度就越 ,数据就越 ,平均数的代表性就越 。
3.方差的单位是原数据单位的 。
4.甲、乙两个样本中,则两个样本的波动情况是( )
A.甲的波动比乙大 B.乙的波动比甲大
C.甲、乙波动一样大 D.无法比较
5.有5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):2,-2,-1,1,0。则这组数据的方差为_____。
田径队的甲乙两名运动员在8次百米跑训练中,成绩如下表:
序数 1 2 3 4 5 6 7 8
甲的成绩/s 12.0 12.2 13.0 12.6 13.1 12.5 12.4 12.2
乙的成绩s 12.2 12.4 12.7 12.5 12.9 12.2 12.8 12.3
序数 1 2 3 4 5 6 7 8
甲/s -0.5 -0.3 0.5 0.1 0.6 0 -0.1 -0.3
乙/s -0.3 -0.1 0.2 0 0.4 -0.3 0.3 -0.2
两人每次训练成绩与平均成绩的差(s)
观察上面的两组数据,你能说出每个数据的实际意义吗?
合作探究
探究一:
离差:
在一组数据中,一个数据与这组数据的平均数的差。
离差可能是正数,可能是负数,也可能是0。
离差的符号和大小反映了该数据偏离平均数的程度。
探究二:
如何利用一组数据中全部数据的离差来反映这组数据的离散程度呢?
怎么办
方案一:
用所有数据的离差之和表示一组数据的离散程度。
甲:
乙:
这是不是偶然现象呢?
设 是数据为x1, x2, x3,……,xn的平均数,n为数据的个数,那么
方案二:
取一组数据中所有数据的离差的绝对值之和。
你同意这种方案吗?说说理由。
(改进的)方案:
离差的平方和的平均数(方差)
方差越大,说明数据的波动越大,越不稳定。
方差用来衡量一组数据的波动大小。(即这组数据偏离平均数的大小)。
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数。
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”。
归纳
(1)已知数据1,4,3,5,2,则这5个数的方差是____。
(2)绝对值小于 的所有整数的方差是______。
(3)一组数据:a, a, a, …,a(有n个a),则它的方差为___。
反馈练习
例:为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,
测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐?
思考:求数据方差的一般步骤是什么?
1.求数据的平均数;
2.利用方差公式求方差。
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
精讲点拨
在一次芭蕾舞的比赛中,甲,乙两个芭蕾舞团表演了舞剧《天鹅舞》,参加表演的女演员的身高(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞女演员的身高更整齐?
试一试
方差越大,说明数据的波动越大,越不稳定。
方差用来衡量一组数据的波动大小
(即这组数据偏离平均数的大小)。
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数。
课堂小结
探索发现
已知三组数据1,2,3,4,5;11,12,13,14,15
和3,6,9,12,15。
1.求这三组数据的平均数和方差。
2.对照以上结果,你能从中发现哪些有趣的结论?
平均数 方差
1,2,3,4,5
11,12,13,14,15
3,6,9,12,15
谢 谢
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
