人教版2019 必修一5.7三角函数的应用 课时精练(附答案)
文档属性
| 名称 | 人教版2019 必修一5.7三角函数的应用 课时精练(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 150.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 11:22:04 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版2019 必修一三角函数的应用课时精练(附答案)
一、单选题
1.将函数 的图象向右平移 个单位,所得图象对应的函数恰为偶函数,则 的最小值为( )
A. B. C. D.
2.在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数和描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是
A. 仍保持平静 B. 不断波动 C. 周期性保持平静 D. 周期性保持波动
3.已知是函数的一条对称轴,且的最大值为 , 则函数( )
A. 最大值是4,最小值是0 B. 最大值是2,最小值是-2
C. 最小值不可能是-4 D. 最大值可能是0
4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为 , 秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
A. y=sin B. y=sin C. y=sin D. y=sin
5.下列结论中正确的是( )
①设 , 是两条不同的直线, , 是两个不同的平面,若 , , ,则 ;
② 是函数 取得最大值的充要条件;
③已知命题 , ;命题 , ,则 为真命题;
④等差数列 中,前 项和为 ,公差 ,若 ,则当 取得最大值时, .
A. ①③ B. ①④ C. ②③ D. ③④
6.已知函数 为 上 的连续函数,当 时, ,当 时, ,且 对 恒成立,函数 的一个周期内的图像与函数 的图像恰好有两个公共点,则 ( )
A. B. C. D.
7.已知线段AB的长为4,以AB为直径的圆有一内接梯形ABCD,其中AB∥CD(如图)则这个梯形的周长的最大值为( )
A. 8 B. 10 C. 4(+1) D. 以上都不对
8.为测量一座塔的高度,在一座与塔相距20米的楼的楼顶处测得塔顶的仰角为30°,测得塔基的俯角为45°,那么塔的高度是( )米.
A. 20 B. 20 C. 20 D. 30
9.若函数的图像关于直线对称,那么a=( )
A. B. - C. 1 D. -1
10.稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+ )+9500 ( >0),已知第一、二季度平均单价如下表所示:
x 1 2 3
y 10000 9500 ?
则此楼群在第三季度的平均单价大约是 ( )
A. 10000元 B. 9500元 C. 9000元 D. 8500元
二、填空题
11.在同一平面直角坐标系中,函数y=cos(+)的图象和直线y=的交点个数是________ 个
12.如图,某港口一天6时到18时的谁深变化曲线近似满足函数y=3sin(x+Φ)+k , 据此函数可知,这段时间水深(单位:m)的最大值为________ .
13.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+Acos[ (x﹣6)](x=1,2,3,…,12)来表示,已知6月份的月平均气温最高为28℃,12月份的月平均气温最低为18℃,则10月份的平均气温值为________℃.
14.已知 , 则=________
三、解答题
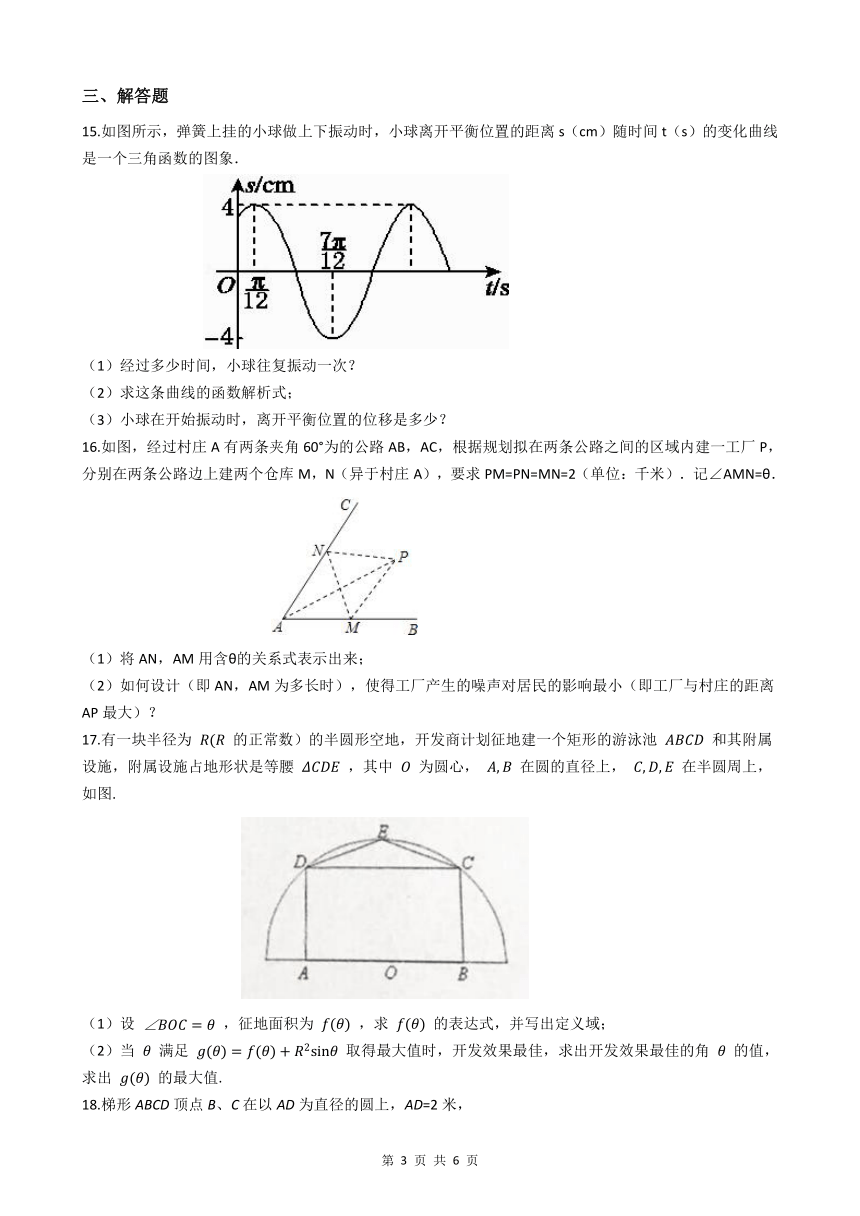
15.如图所示,弹簧上挂的小球做上下振动时,小球离开平衡位置的距离s(cm)随时间t(s)的变化曲线是一个三角函数的图象.
(1)经过多少时间,小球往复振动一次?
(2)求这条曲线的函数解析式;
(3)小球在开始振动时,离开平衡位置的位移是多少?
16.如图,经过村庄A有两条夹角60°为的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).记∠AMN=θ.
(1)将AN,AM用含θ的关系式表示出来;
(2)如何设计(即AN,AM为多长时),使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离AP最大)?
17.有一块半径为 的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池 和其附属设施,附属设施占地形状是等腰 ,其中 为圆心, 在圆的直径上, 在半圆周上,如图.
(1)设 ,征地面积为 ,求 的表达式,并写出定义域;
(2)当 满足 取得最大值时,开发效果最佳,求出开发效果最佳的角 的值,求出 的最大值.
18.梯形ABCD顶点B、C在以AD为直径的圆上,AD=2米,
(1)如图1,若电热丝由AB , BC , CD这三部分组成,在AB , CD上每米可辐射1单位热量,在BC上每米可辐射2单位热量,请设计BC的长度,使得电热丝辐射的总热量最大,并求总热量的最大值;
(2)如图2,若电热丝由弧 和弦BC这三部分组成,在弧 上每米可辐射1单位热量,在弦BC上每米可辐射2单位热量,请设计BC的长度,使得电热丝辐射的总热量最大.
19.如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这一天的最大温差;
(2)写出这段曲线的函数解析式.
20.如图所示为一个观览车示意图,该观览车半径为 ,圆上最低点与地面距离为 , 秒转动一圈,图中 与地面垂直,以 为始边,逆时针转动 角到 ,设 点与地面距离为 .
(1)求 与 间关系的函数解析式;
(2)设从 开始转动,经过 秒到达 ,求 与 间关系的函数解析式.
答案
一、单选题
1. B 2. A 3. D 4. C 5. A 6. A 7. B 8. A 9. D 10. C
二、填空题
11. 2 12. 8 13. 20.5 14.
三、解答题
15. (1)解:由函数的图象可得函数的周期T=2( ﹣ )=π,故小球往复运动一次需π
(2)解:由题意设这条曲线的函数解析式为:s=Asin(ωt+φ) (其中Α>0,ω>0,|φ|≤π),
由图象可知A=4,T=π,所以ω= = =2,
因为函数经过( ,4);
所以4=4sin(2× +φ),可得:2× +φ=2kπ+ ,k∈Z,解得:φ=2kπ+ ,k∈Z,
所以φ= ,s=4sin(2t+ )
(3)解:因为s=4sin(2t+ ), 所以由题意可得当t=0时,s=4sin(0+ )=2,
故小球在开始振动时,离开平衡位置的位移是2
16. (1)解:∠AMN=θ,在△AMN中,由正弦定理得: = =
所以AN= ,AM=
(2)解:AP2=AM2+MP2﹣2AM MP cos∠AMP
= sin2(θ+60°)+4﹣ sin(θ+60°)cos(θ+60°)
= [1﹣cos(2θ+120°)]﹣ sin(2θ+120°)+4= [ sin(2θ+120°)+cos(2θ+120°)]+
= ﹣ sin(2θ+150°),θ∈(0°,120°)(其中利用诱导公式可知sin(120°﹣θ)=sin(θ+60°))
当且仅当2θ+150°=270°,即θ=60°时,工厂产生的噪声对居民的影响最小,此时AN=AM=2.
17. (1)解:连接 ,
在 中, ,
因为 ,
(2)解: ,
令 ,因为 ,所以 ,
所以
因为 在 上单调递增,所以 时 有最大值为 ,此时
18. (1)解:设∠AOB=θ,θ∈(0, )则AB=2sin ,BC=2cosθ, 总热量单位f(θ) =4cosθ+4 sin =-8(sin )2+4 sin +4,当sin = , 此时BC=2cosθ= (米),总热量最大 (单位) . 答:应设计BC长为 米,电热丝辐射的总热量最大,最大值为 单位
(2)解:总热量单位g(θ)=2θ+4cosθ,θ∈(0, ) 令g'(θ)=0,即2-4sinθ=0,θ= ,增区间(0, ),减区间( , ) 当θ= ,g(θ)最大,此时BC=2cosθ= (米) 答:应设计BC长为 米,电热丝辐射的总热量最大
19. 解:(1)由图示,这段时间的最大温差是30℃﹣10℃=20℃,
(2)图中从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期,
∴=14﹣6,解得ω= ,
由图示,A=(30﹣10)=10,B=(10+30)=20,这时,y=10sin(x+φ)+20,
将x=6,y=10代入上式,可取φ= ,
综上,所求的解析式为y=10sin(x+)+20,x∈[6,14].
20. (1)解:过点 作地面的平行线 ,过点 作 的垂线 交 于 点.
当 时, , ;
当 , 时,上述解析式也适合.综上所述,
(2)解:点 在 上逆时针运动的角速度是 ,∴ 秒转过的弧度数为 ,
∴
(
第
1
页 共
8
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版2019 必修一三角函数的应用课时精练(附答案)
一、单选题
1.将函数 的图象向右平移 个单位,所得图象对应的函数恰为偶函数,则 的最小值为( )
A. B. C. D.
2.在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数和描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是
A. 仍保持平静 B. 不断波动 C. 周期性保持平静 D. 周期性保持波动
3.已知是函数的一条对称轴,且的最大值为 , 则函数( )
A. 最大值是4,最小值是0 B. 最大值是2,最小值是-2
C. 最小值不可能是-4 D. 最大值可能是0
4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为 , 秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
A. y=sin B. y=sin C. y=sin D. y=sin
5.下列结论中正确的是( )
①设 , 是两条不同的直线, , 是两个不同的平面,若 , , ,则 ;
② 是函数 取得最大值的充要条件;
③已知命题 , ;命题 , ,则 为真命题;
④等差数列 中,前 项和为 ,公差 ,若 ,则当 取得最大值时, .
A. ①③ B. ①④ C. ②③ D. ③④
6.已知函数 为 上 的连续函数,当 时, ,当 时, ,且 对 恒成立,函数 的一个周期内的图像与函数 的图像恰好有两个公共点,则 ( )
A. B. C. D.
7.已知线段AB的长为4,以AB为直径的圆有一内接梯形ABCD,其中AB∥CD(如图)则这个梯形的周长的最大值为( )
A. 8 B. 10 C. 4(+1) D. 以上都不对
8.为测量一座塔的高度,在一座与塔相距20米的楼的楼顶处测得塔顶的仰角为30°,测得塔基的俯角为45°,那么塔的高度是( )米.
A. 20 B. 20 C. 20 D. 30
9.若函数的图像关于直线对称,那么a=( )
A. B. - C. 1 D. -1
10.稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+ )+9500 ( >0),已知第一、二季度平均单价如下表所示:
x 1 2 3
y 10000 9500 ?
则此楼群在第三季度的平均单价大约是 ( )
A. 10000元 B. 9500元 C. 9000元 D. 8500元
二、填空题
11.在同一平面直角坐标系中,函数y=cos(+)的图象和直线y=的交点个数是________ 个
12.如图,某港口一天6时到18时的谁深变化曲线近似满足函数y=3sin(x+Φ)+k , 据此函数可知,这段时间水深(单位:m)的最大值为________ .
13.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+Acos[ (x﹣6)](x=1,2,3,…,12)来表示,已知6月份的月平均气温最高为28℃,12月份的月平均气温最低为18℃,则10月份的平均气温值为________℃.
14.已知 , 则=________
三、解答题
15.如图所示,弹簧上挂的小球做上下振动时,小球离开平衡位置的距离s(cm)随时间t(s)的变化曲线是一个三角函数的图象.
(1)经过多少时间,小球往复振动一次?
(2)求这条曲线的函数解析式;
(3)小球在开始振动时,离开平衡位置的位移是多少?
16.如图,经过村庄A有两条夹角60°为的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).记∠AMN=θ.
(1)将AN,AM用含θ的关系式表示出来;
(2)如何设计(即AN,AM为多长时),使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离AP最大)?
17.有一块半径为 的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池 和其附属设施,附属设施占地形状是等腰 ,其中 为圆心, 在圆的直径上, 在半圆周上,如图.
(1)设 ,征地面积为 ,求 的表达式,并写出定义域;
(2)当 满足 取得最大值时,开发效果最佳,求出开发效果最佳的角 的值,求出 的最大值.
18.梯形ABCD顶点B、C在以AD为直径的圆上,AD=2米,
(1)如图1,若电热丝由AB , BC , CD这三部分组成,在AB , CD上每米可辐射1单位热量,在BC上每米可辐射2单位热量,请设计BC的长度,使得电热丝辐射的总热量最大,并求总热量的最大值;
(2)如图2,若电热丝由弧 和弦BC这三部分组成,在弧 上每米可辐射1单位热量,在弦BC上每米可辐射2单位热量,请设计BC的长度,使得电热丝辐射的总热量最大.
19.如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这一天的最大温差;
(2)写出这段曲线的函数解析式.
20.如图所示为一个观览车示意图,该观览车半径为 ,圆上最低点与地面距离为 , 秒转动一圈,图中 与地面垂直,以 为始边,逆时针转动 角到 ,设 点与地面距离为 .
(1)求 与 间关系的函数解析式;
(2)设从 开始转动,经过 秒到达 ,求 与 间关系的函数解析式.
答案
一、单选题
1. B 2. A 3. D 4. C 5. A 6. A 7. B 8. A 9. D 10. C
二、填空题
11. 2 12. 8 13. 20.5 14.
三、解答题
15. (1)解:由函数的图象可得函数的周期T=2( ﹣ )=π,故小球往复运动一次需π
(2)解:由题意设这条曲线的函数解析式为:s=Asin(ωt+φ) (其中Α>0,ω>0,|φ|≤π),
由图象可知A=4,T=π,所以ω= = =2,
因为函数经过( ,4);
所以4=4sin(2× +φ),可得:2× +φ=2kπ+ ,k∈Z,解得:φ=2kπ+ ,k∈Z,
所以φ= ,s=4sin(2t+ )
(3)解:因为s=4sin(2t+ ), 所以由题意可得当t=0时,s=4sin(0+ )=2,
故小球在开始振动时,离开平衡位置的位移是2
16. (1)解:∠AMN=θ,在△AMN中,由正弦定理得: = =
所以AN= ,AM=
(2)解:AP2=AM2+MP2﹣2AM MP cos∠AMP
= sin2(θ+60°)+4﹣ sin(θ+60°)cos(θ+60°)
= [1﹣cos(2θ+120°)]﹣ sin(2θ+120°)+4= [ sin(2θ+120°)+cos(2θ+120°)]+
= ﹣ sin(2θ+150°),θ∈(0°,120°)(其中利用诱导公式可知sin(120°﹣θ)=sin(θ+60°))
当且仅当2θ+150°=270°,即θ=60°时,工厂产生的噪声对居民的影响最小,此时AN=AM=2.
17. (1)解:连接 ,
在 中, ,
因为 ,
(2)解: ,
令 ,因为 ,所以 ,
所以
因为 在 上单调递增,所以 时 有最大值为 ,此时
18. (1)解:设∠AOB=θ,θ∈(0, )则AB=2sin ,BC=2cosθ, 总热量单位f(θ) =4cosθ+4 sin =-8(sin )2+4 sin +4,当sin = , 此时BC=2cosθ= (米),总热量最大 (单位) . 答:应设计BC长为 米,电热丝辐射的总热量最大,最大值为 单位
(2)解:总热量单位g(θ)=2θ+4cosθ,θ∈(0, ) 令g'(θ)=0,即2-4sinθ=0,θ= ,增区间(0, ),减区间( , ) 当θ= ,g(θ)最大,此时BC=2cosθ= (米) 答:应设计BC长为 米,电热丝辐射的总热量最大
19. 解:(1)由图示,这段时间的最大温差是30℃﹣10℃=20℃,
(2)图中从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期,
∴=14﹣6,解得ω= ,
由图示,A=(30﹣10)=10,B=(10+30)=20,这时,y=10sin(x+φ)+20,
将x=6,y=10代入上式,可取φ= ,
综上,所求的解析式为y=10sin(x+)+20,x∈[6,14].
20. (1)解:过点 作地面的平行线 ,过点 作 的垂线 交 于 点.
当 时, , ;
当 , 时,上述解析式也适合.综上所述,
(2)解:点 在 上逆时针运动的角速度是 ,∴ 秒转过的弧度数为 ,
∴
(
第
1
页 共
8
页
)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
