6.4用树状图计算概率
图片预览







文档简介
课件21张PPT。第6章:频率与概率6.4用树状图计算概率 2.三种事件发生的概率及表示?1.一个事件发生的可能性的大小可以用一个数来表示,我们把这个数叫做这个事件发生的_____,一般用P(事件)表示。事件A发生的概率也记为P(A),事件B发生的概率记为P(B) ,依此类推. 1001概率新课标教学网(www.xkbw.com)--海量教学资源欢迎下载! 3.有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则: p (摸到1号卡片)= ;p (摸到2号卡片)= ;p (摸到3号卡片)= ; p (摸到4号卡片)= ;p (摸到奇数号卡片)= ; P(摸到偶数号卡片) = .新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!4.P(正上方数字是6)= ;P(正上方数字是1或2)=____;P(正上方数字是偶数)=____ 。 新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!1. 能理解随着试验次数的增加,事件发生的频率与概率的关系。
2.会用列举法(包括列表,画树状图)列出简单随机事件所有可能结果,以及指定事件的所有结果。
3.能通过列表、画树状图的方法求简单事件的概率.学习目标:学习重点:
通过列表、画树状图的方法求简单事件的概率.
学习难点:
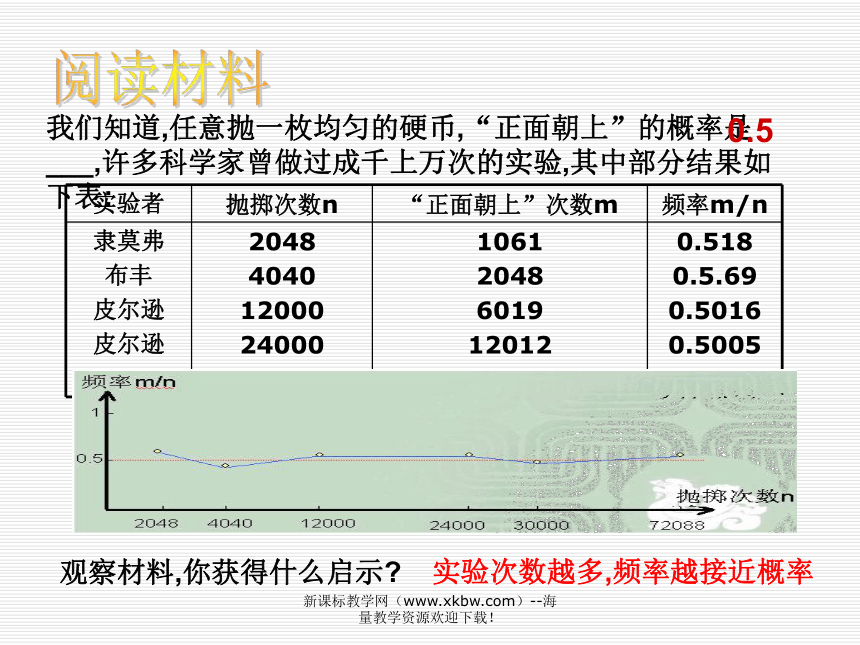
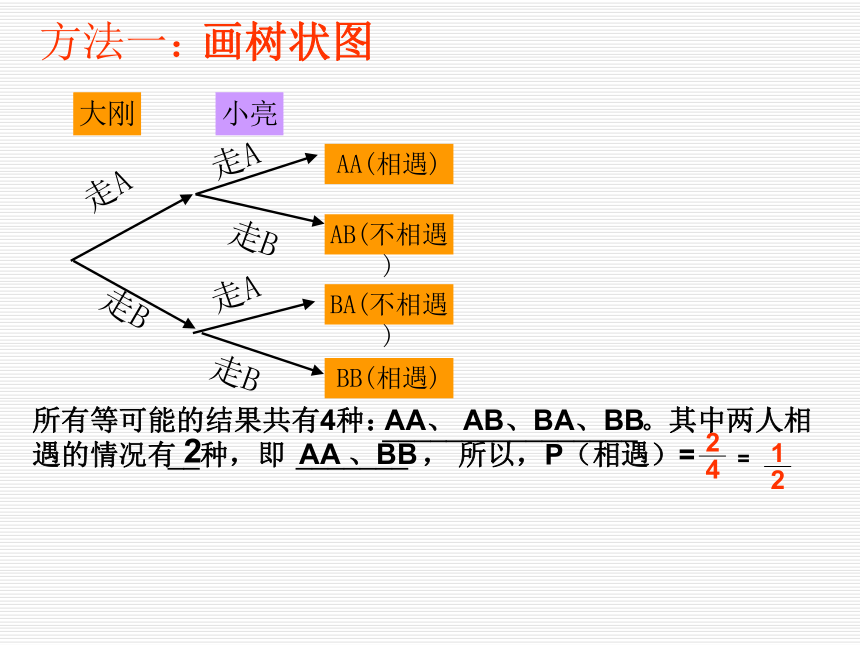
求三次和区分有无放回事件的概率。阅读材料我们知道,任意抛一枚均匀的硬币,“正面朝上”的概率是___,许多科学家曾做过成千上万次的实验,其中部分结果如下表:观察材料,你获得什么启示?实验次数越多,频率越接近概率0.5新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!自学探究问题:AABB 大刚小亮AA(相遇)AB(不相遇)BA(不相遇)BB(相遇)走A走B走A走B走A走B方法一:所有等可能的结果共有4种: 。其中两人相遇的情况有 种,即 , 所以,P(相遇)=2AA、 AB、BA、BBAA 、BB 画树状图=_________________________如果将小亮和大刚顺序交换,那么你会画树状图吗?试一试,求得他们途中相遇的概率是多少?与顺序有关吗?
你学会画树状图 求概率了吗? 上面的问题,除上述方法外,还可以通过列表分析出所有等可能的结果。
走A走B走B走A小亮大刚表中的第1行表示小亮走道路A或B的两种可能表中的第1列表示大刚走道路A或B的两种可能ABAABABB从而在表中列出了所有等可能的4种结果,即AA、AB、BA、BB,其中二人相遇的结果有2种。于是P(相遇)= = 方法2 ——列表法想一想:用树状图和列表法来计算概率,有什么优点?利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.画出树状图:所以,P(积为0)=列表如下: 所以P(积为0)= 由树状图可知,共有6种等可能的结果,其中“同色”有2种. 所以P(同色)=1.BACAABACBCCCBB课堂练习2.袋子里有两个黑球和一个白球,有放回地连续两次从中摸出一个,共有几种可能性?两次都摸到白球的概率是多少?摸到一黑一白的概率是多少?3.随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少?更上一城楼2.随机掷一枚均匀的硬币三次,至少有一次正面朝上的概率是多少?1.说明:取两个=连续两次取一个(即无放回)说明:掷一枚硬币三次=掷三枚硬币各一次
回味无穷 利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.当试验包含两步时,_____法比较方便,当然,此时也可以________法,当试验在三步或三步以上时,只能用_________法方便.用列表法和树状图法求概率时应注意什么情况?列表画树状图画树状图我知道了……
我学会了……
我能解决……
我用列表法和树状图法求概率时应注意什么 ……课本78页 习题6.4 A组 1.(1)(2) 2.鲜花为你盛开,你一定行!谢谢同学们的精彩表现再见谢谢老师的指导
2.会用列举法(包括列表,画树状图)列出简单随机事件所有可能结果,以及指定事件的所有结果。
3.能通过列表、画树状图的方法求简单事件的概率.学习目标:学习重点:
通过列表、画树状图的方法求简单事件的概率.
学习难点:
求三次和区分有无放回事件的概率。阅读材料我们知道,任意抛一枚均匀的硬币,“正面朝上”的概率是___,许多科学家曾做过成千上万次的实验,其中部分结果如下表:观察材料,你获得什么启示?实验次数越多,频率越接近概率0.5新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!自学探究问题:AABB 大刚小亮AA(相遇)AB(不相遇)BA(不相遇)BB(相遇)走A走B走A走B走A走B方法一:所有等可能的结果共有4种: 。其中两人相遇的情况有 种,即 , 所以,P(相遇)=2AA、 AB、BA、BBAA 、BB 画树状图=_________________________如果将小亮和大刚顺序交换,那么你会画树状图吗?试一试,求得他们途中相遇的概率是多少?与顺序有关吗?
你学会画树状图 求概率了吗? 上面的问题,除上述方法外,还可以通过列表分析出所有等可能的结果。
走A走B走B走A小亮大刚表中的第1行表示小亮走道路A或B的两种可能表中的第1列表示大刚走道路A或B的两种可能ABAABABB从而在表中列出了所有等可能的4种结果,即AA、AB、BA、BB,其中二人相遇的结果有2种。于是P(相遇)= = 方法2 ——列表法想一想:用树状图和列表法来计算概率,有什么优点?利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.画出树状图:所以,P(积为0)=列表如下: 所以P(积为0)= 由树状图可知,共有6种等可能的结果,其中“同色”有2种. 所以P(同色)=1.BACAABACBCCCBB课堂练习2.袋子里有两个黑球和一个白球,有放回地连续两次从中摸出一个,共有几种可能性?两次都摸到白球的概率是多少?摸到一黑一白的概率是多少?3.随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少?更上一城楼2.随机掷一枚均匀的硬币三次,至少有一次正面朝上的概率是多少?1.说明:取两个=连续两次取一个(即无放回)说明:掷一枚硬币三次=掷三枚硬币各一次
回味无穷 利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.当试验包含两步时,_____法比较方便,当然,此时也可以________法,当试验在三步或三步以上时,只能用_________法方便.用列表法和树状图法求概率时应注意什么情况?列表画树状图画树状图我知道了……
我学会了……
我能解决……
我用列表法和树状图法求概率时应注意什么 ……课本78页 习题6.4 A组 1.(1)(2) 2.鲜花为你盛开,你一定行!谢谢同学们的精彩表现再见谢谢老师的指导
