人教版(2019)数学选择性必修第一册 3.2.2双曲线的简单几何性质 课件(共38张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修第一册 3.2.2双曲线的简单几何性质 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 14:17:31 | ||
图片预览











文档简介
(共38张PPT)
双曲线的简单几何性质
1.掌握双曲线的简单几何性质.
2.了解双曲线的渐近性及渐近线的概念.
3.能区别椭圆与双曲线的性质.
本节目标
课前预习
预习课本P121~124,思考并完成以下问题
1.双曲线有哪些几何性质?
2.双曲线的顶点、实轴、虚轴分别是什么?
3.双曲线的渐近线、等轴双曲线的定义分别是什么?
课前小测
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)双曲线=1的焦点在y轴上( )
(2)双曲线的离心率越大,双曲线的开口越开阔( )
(3)以y=±2x为渐近线的双曲线有2条( )
×
√
×
2.双曲线-y2=1的顶点坐标是( )
A.(4,0),(0,1) B.(-4,0),(4,0)
C.(0,1),(0,-1) D.(-4,0),(0,-1)
B
3.中心在原点,实轴长为10,虚轴长为6的双曲线的标准方程是( )
A. =1 B. - =1或- =1
C. - =1 D. - =1或- =1
B
4.(全国卷Ⅲ)双曲线=1(a>0)的一条渐近线方程为y= x,则a=________.
5
新知探究
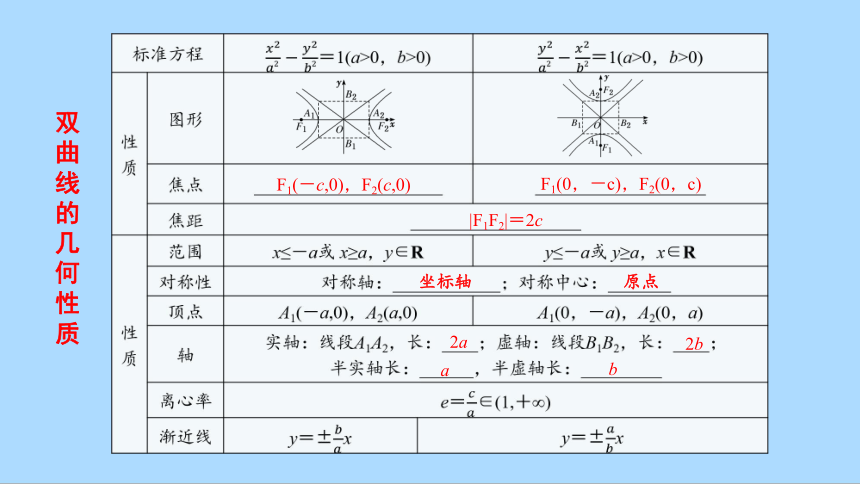
双曲线的几何性质
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
|F1F2|=2c
坐标轴
原点
2a
2b
a
b
等轴双曲线
实轴和虚轴______的双曲线叫等轴双曲线,它的渐近线是_________,离心率为e=______.
等长
y=±x
对双曲线的简单几何性质的几点认识
(1)双曲线的焦点决定双曲线的位置;
(2)双曲线的离心率和渐近线刻画了双曲线的开口大小,离心率越大,双曲线的开口越大,反之亦然.
知识点睛
题型突破
典例深度剖析 重点多维探究
[例1] 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.
题型一 已知方程求其几何性质
[例1] 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.
将9y2-4x2=-36变形为=1,即=1,
∴a=3,b=2,c=,
因此顶点为A1(-3,0),A2(3,0),焦点坐标为F1(-,0),F2(,0),
实轴长是2a=6,虚轴长是2b=4,
离心率e==,
渐近线方程y=±x.作草图如图所示.
归纳总结
由双曲线的标准方程求几何性质的四个步骤
跟踪训练
1.已知双曲线x2-ky2=1的一个焦点是(,0),则其渐近线方程为( )
A.y=±x B.y=±4x
C.y=±x D.y=±2x
D
双曲线方程化为x2- =1,由题意可得,1+=5,解得k=,即双曲线方程为x2- =1,则其渐近线方程为y=±2x.
题型二 利用几何性质求双曲线的标准方程
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
(1)双曲线过点(3, 9),离心率e=;
(2)与双曲线x2-2y2=2有共同的渐近线,且经过点(2,-2);
(3)过点P(2,-1),渐近线方程是y=±3x.
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
(1)双曲线过点(3, 9),离心率e=;
由e2=,得=,
设a2=9k(k>0),则c2=10k,b2=c2-a2=k.
设所求双曲线方程为=1①或=1②.
把(3,9)代入①,得k=-161,与k>0矛盾,无解;
把(3,9)代入②,得k=9.
故所求双曲线方程为=1.
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
(2)与双曲线x2-2y2=2有共同的渐近线,且经过点(2,-2);
设所求双曲线方程为x2-2y2=k.③
由于双曲线过点(2,-2),
将(2,-2)代入③,得k=22-2·(-2)2=-4.
故所求双曲线方程为x2-2y2=-4,即=1.
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
由渐近线方程可设所求双曲线方程为-y2=λ(λ≠0).④
将点P(2,-1)代入④,得λ=35,
故所求的双曲线方程为- =1.
(3)过点P(2,-1),渐近线方程是y=±3x.
归纳总结
待定系数法求双曲线标准方程的步骤
根据渐近线方程求双曲线方程
(1)若双曲线的渐近线方程为y=±x,则双曲线方程可表示为- =λ(λ≠0).
(2)与双曲线- =1(a>0,b>0)有共同渐近线的双曲线方程可表示为-=λ(a>0,b>0,λ≠0);与双曲线-=1(a>0,b>0)有共同渐近线的双曲线方程可表示为-=λ(a>0,b>0,λ≠0).
技巧点拨
跟踪训练
2. 双曲线- =1(a>0,b>0)的离心率为2,原点到直线AB的距离为,其中A(0,-b),B(a,0),求该双曲线的标准方程.
∵e=2,∴1+ =4,∴b2=3a2.①
又∵AB的方程为bx-ay-ab=0,
由点到直线的距离公式,可得= ,②
由①②联立,可解得a2=1,b2=3,
∴双曲线方程为x2- =1.
[例3] (1)已知双曲线=1(a>)的两条渐近线的夹角为,则双曲线的离心率为( )
A. B.
C. D.2
题型三 双曲线的离心率、渐近线
A
[例3] (1)已知双曲线=1(a>)的两条渐近线的夹角为,则双曲线的离心率为( )
A. B.
C. D.2
A
双曲线=1(a>)的两条渐近线方程为y=±x.
由a>,得0< <1,
∴直线y= x的倾斜角小于.
∴ =tan = ,解得a=.
又c2=a2+2=8,∴c=2,∴e= = .
(2)若F1,F2是双曲线- =1(a>0,b>0)与椭圆+=1的共同的左、右焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是( )
A.3x±y=0 B. x±3y=0
C.3x± y=0 D. x±3y=0
D
又双曲线的焦点在x轴上,故所对应的渐近线方程为y=±x,
(2)若F1,F2是双曲线- =1(a>0,b>0)与椭圆+=1的共同的左、右焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是( )
A.3x±y=0 B. x±3y=0
C.3x± y=0 D. x±3y=0
由题意得F1(-4,0),F2(4,0),故双曲线中c=4,
如图所示,若△PF1F2为等腰三角形,
则需满足|PF1|=|F1F2|=8,
化为一般式方程为x±3y=0.
依据椭圆与双曲线的定义应有
|PF1| + |PF2|=10
|PF1| - |PF2|=2a
解得a=3,
故b== ,
D
(3)设F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(+)· =0(O为坐标原点),且||= ||,则该双曲线的离心率为________.
∵(+ )· =0,∴OB⊥PF2,且B为PF2的中点.
又O是F1F2的中点,∴OB∥PF1,∴PF1⊥PF2.
∵|PF1|-|PF2|=2a,又∵| |= ||,
∴|PF2|=(+1)a,|PF1|=(+3)a.
∴由|PF1|2+|PF2|2=|F1F2|2,得(12+6)a2+(4+2)a2=4c2,
∴e2=4+2,∴e=+1.
②利用e= 求解;
(1)①依据条件求出a,c,利用e=求解;
③依据条件,建立关于a,b,c的齐次关系式,消去b转化为离心率e的方程求解.
(2)求离心率的范围,常结合已知条件构建关于a,b,c的不等关系.
求双曲线离心率的常见方法
方法总结
方法总结
求双曲线渐近线方程的两种方法
跟踪训练
3.已知F1,F2是双曲线-=1(a>0,b>0)的左、右焦点,点P在双曲线上且不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A.若|OA|=b,则该双曲线的离心率为________.
如图所示,延长F2A交PF1于点B.
依题意可得|BF1|=|PF1|-|PF2|=2a.
又因为点A是BF2的中点,所以|OA|=|BF1|,
所以b=a.所以c=a.所以离心率为.
随堂检测
1.(全国新课标Ⅰ)已知双曲线C:-=1(a>0,b>0)的离心率为,则C的渐近线方程为( )
A.y=±x B.y=± x
C.y=±x D.y=±x
因为双曲线-=1的焦点在x轴上,
所以双曲线的渐近线方程为y=±x.
又离心率e== = = ,所以= ,
所以双曲线的渐近线方程为y=± x.
C
2.已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于,则C的方程是( )
A. -=1 B. -=1
C. -=1 D. -=1
由题意可知c=3,a=2,b= = = ,
故双曲线的方程为-=1.
B
3.已知0<θ< ,则双曲线C1: =1与C2: - =1的( )
A.实轴长相等 B.虚轴长相等
C.焦距相等 D.离心率相等
D
4.设F1,F2分别为双曲线-=1(a>0,b>0)的左、右焦点,双曲线上存在一点P使得|PF1|+|PF2|=3b,|PF1|·|PF2|= ab,则该双曲线的离心率为( )
A. B. C. D.3
B
依题意得|PF1|-|PF2|=±2a,又|PF1|+|PF2|=3b,
(|PF1|+|PF2|)2-(|PF1|-|PF2|)2=9b2-4a2,即有4|PF1|·|PF2|=9b2-4a2,
又4|PF1|·|PF2|=9ab,因此有9b2-4a2=9ab,
即9--4=0,( +1) (-4) =0, = ,
该双曲线的离心率e== .
(1)双曲线的范围反映了其图象是两支,且在范围内向两方无限延伸.
(2)双曲线既是中心对称图形,又是轴对称图形,(0,0)为对称中心,坐标轴为对称轴.
(3) 双曲线的离心率e=反映了双曲线开口的大小,e越大,双曲线的开口就越大.
(4) 双曲线的渐近线是两条直线,当x,y趋向于无穷大时,双曲线将无限地与渐近线接近,但永远没有交点.
本课小结
对双曲线的几何性质的四点说明
本课小结
双曲线与椭圆的六点不同
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实轴、虚轴 长轴、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0a,b,c关系 a2+b2=c2 a2-b2=c2
通过本节课,你学会了什么?
双曲线的简单几何性质
1.掌握双曲线的简单几何性质.
2.了解双曲线的渐近性及渐近线的概念.
3.能区别椭圆与双曲线的性质.
本节目标
课前预习
预习课本P121~124,思考并完成以下问题
1.双曲线有哪些几何性质?
2.双曲线的顶点、实轴、虚轴分别是什么?
3.双曲线的渐近线、等轴双曲线的定义分别是什么?
课前小测
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)双曲线=1的焦点在y轴上( )
(2)双曲线的离心率越大,双曲线的开口越开阔( )
(3)以y=±2x为渐近线的双曲线有2条( )
×
√
×
2.双曲线-y2=1的顶点坐标是( )
A.(4,0),(0,1) B.(-4,0),(4,0)
C.(0,1),(0,-1) D.(-4,0),(0,-1)
B
3.中心在原点,实轴长为10,虚轴长为6的双曲线的标准方程是( )
A. =1 B. - =1或- =1
C. - =1 D. - =1或- =1
B
4.(全国卷Ⅲ)双曲线=1(a>0)的一条渐近线方程为y= x,则a=________.
5
新知探究
双曲线的几何性质
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
|F1F2|=2c
坐标轴
原点
2a
2b
a
b
等轴双曲线
实轴和虚轴______的双曲线叫等轴双曲线,它的渐近线是_________,离心率为e=______.
等长
y=±x
对双曲线的简单几何性质的几点认识
(1)双曲线的焦点决定双曲线的位置;
(2)双曲线的离心率和渐近线刻画了双曲线的开口大小,离心率越大,双曲线的开口越大,反之亦然.
知识点睛
题型突破
典例深度剖析 重点多维探究
[例1] 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.
题型一 已知方程求其几何性质
[例1] 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.
将9y2-4x2=-36变形为=1,即=1,
∴a=3,b=2,c=,
因此顶点为A1(-3,0),A2(3,0),焦点坐标为F1(-,0),F2(,0),
实轴长是2a=6,虚轴长是2b=4,
离心率e==,
渐近线方程y=±x.作草图如图所示.
归纳总结
由双曲线的标准方程求几何性质的四个步骤
跟踪训练
1.已知双曲线x2-ky2=1的一个焦点是(,0),则其渐近线方程为( )
A.y=±x B.y=±4x
C.y=±x D.y=±2x
D
双曲线方程化为x2- =1,由题意可得,1+=5,解得k=,即双曲线方程为x2- =1,则其渐近线方程为y=±2x.
题型二 利用几何性质求双曲线的标准方程
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
(1)双曲线过点(3, 9),离心率e=;
(2)与双曲线x2-2y2=2有共同的渐近线,且经过点(2,-2);
(3)过点P(2,-1),渐近线方程是y=±3x.
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
(1)双曲线过点(3, 9),离心率e=;
由e2=,得=,
设a2=9k(k>0),则c2=10k,b2=c2-a2=k.
设所求双曲线方程为=1①或=1②.
把(3,9)代入①,得k=-161,与k>0矛盾,无解;
把(3,9)代入②,得k=9.
故所求双曲线方程为=1.
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
(2)与双曲线x2-2y2=2有共同的渐近线,且经过点(2,-2);
设所求双曲线方程为x2-2y2=k.③
由于双曲线过点(2,-2),
将(2,-2)代入③,得k=22-2·(-2)2=-4.
故所求双曲线方程为x2-2y2=-4,即=1.
[例2] 求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:
由渐近线方程可设所求双曲线方程为-y2=λ(λ≠0).④
将点P(2,-1)代入④,得λ=35,
故所求的双曲线方程为- =1.
(3)过点P(2,-1),渐近线方程是y=±3x.
归纳总结
待定系数法求双曲线标准方程的步骤
根据渐近线方程求双曲线方程
(1)若双曲线的渐近线方程为y=±x,则双曲线方程可表示为- =λ(λ≠0).
(2)与双曲线- =1(a>0,b>0)有共同渐近线的双曲线方程可表示为-=λ(a>0,b>0,λ≠0);与双曲线-=1(a>0,b>0)有共同渐近线的双曲线方程可表示为-=λ(a>0,b>0,λ≠0).
技巧点拨
跟踪训练
2. 双曲线- =1(a>0,b>0)的离心率为2,原点到直线AB的距离为,其中A(0,-b),B(a,0),求该双曲线的标准方程.
∵e=2,∴1+ =4,∴b2=3a2.①
又∵AB的方程为bx-ay-ab=0,
由点到直线的距离公式,可得= ,②
由①②联立,可解得a2=1,b2=3,
∴双曲线方程为x2- =1.
[例3] (1)已知双曲线=1(a>)的两条渐近线的夹角为,则双曲线的离心率为( )
A. B.
C. D.2
题型三 双曲线的离心率、渐近线
A
[例3] (1)已知双曲线=1(a>)的两条渐近线的夹角为,则双曲线的离心率为( )
A. B.
C. D.2
A
双曲线=1(a>)的两条渐近线方程为y=±x.
由a>,得0< <1,
∴直线y= x的倾斜角小于.
∴ =tan = ,解得a=.
又c2=a2+2=8,∴c=2,∴e= = .
(2)若F1,F2是双曲线- =1(a>0,b>0)与椭圆+=1的共同的左、右焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是( )
A.3x±y=0 B. x±3y=0
C.3x± y=0 D. x±3y=0
D
又双曲线的焦点在x轴上,故所对应的渐近线方程为y=±x,
(2)若F1,F2是双曲线- =1(a>0,b>0)与椭圆+=1的共同的左、右焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是( )
A.3x±y=0 B. x±3y=0
C.3x± y=0 D. x±3y=0
由题意得F1(-4,0),F2(4,0),故双曲线中c=4,
如图所示,若△PF1F2为等腰三角形,
则需满足|PF1|=|F1F2|=8,
化为一般式方程为x±3y=0.
依据椭圆与双曲线的定义应有
|PF1| + |PF2|=10
|PF1| - |PF2|=2a
解得a=3,
故b== ,
D
(3)设F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(+)· =0(O为坐标原点),且||= ||,则该双曲线的离心率为________.
∵(+ )· =0,∴OB⊥PF2,且B为PF2的中点.
又O是F1F2的中点,∴OB∥PF1,∴PF1⊥PF2.
∵|PF1|-|PF2|=2a,又∵| |= ||,
∴|PF2|=(+1)a,|PF1|=(+3)a.
∴由|PF1|2+|PF2|2=|F1F2|2,得(12+6)a2+(4+2)a2=4c2,
∴e2=4+2,∴e=+1.
②利用e= 求解;
(1)①依据条件求出a,c,利用e=求解;
③依据条件,建立关于a,b,c的齐次关系式,消去b转化为离心率e的方程求解.
(2)求离心率的范围,常结合已知条件构建关于a,b,c的不等关系.
求双曲线离心率的常见方法
方法总结
方法总结
求双曲线渐近线方程的两种方法
跟踪训练
3.已知F1,F2是双曲线-=1(a>0,b>0)的左、右焦点,点P在双曲线上且不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A.若|OA|=b,则该双曲线的离心率为________.
如图所示,延长F2A交PF1于点B.
依题意可得|BF1|=|PF1|-|PF2|=2a.
又因为点A是BF2的中点,所以|OA|=|BF1|,
所以b=a.所以c=a.所以离心率为.
随堂检测
1.(全国新课标Ⅰ)已知双曲线C:-=1(a>0,b>0)的离心率为,则C的渐近线方程为( )
A.y=±x B.y=± x
C.y=±x D.y=±x
因为双曲线-=1的焦点在x轴上,
所以双曲线的渐近线方程为y=±x.
又离心率e== = = ,所以= ,
所以双曲线的渐近线方程为y=± x.
C
2.已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于,则C的方程是( )
A. -=1 B. -=1
C. -=1 D. -=1
由题意可知c=3,a=2,b= = = ,
故双曲线的方程为-=1.
B
3.已知0<θ< ,则双曲线C1: =1与C2: - =1的( )
A.实轴长相等 B.虚轴长相等
C.焦距相等 D.离心率相等
D
4.设F1,F2分别为双曲线-=1(a>0,b>0)的左、右焦点,双曲线上存在一点P使得|PF1|+|PF2|=3b,|PF1|·|PF2|= ab,则该双曲线的离心率为( )
A. B. C. D.3
B
依题意得|PF1|-|PF2|=±2a,又|PF1|+|PF2|=3b,
(|PF1|+|PF2|)2-(|PF1|-|PF2|)2=9b2-4a2,即有4|PF1|·|PF2|=9b2-4a2,
又4|PF1|·|PF2|=9ab,因此有9b2-4a2=9ab,
即9--4=0,( +1) (-4) =0, = ,
该双曲线的离心率e== .
(1)双曲线的范围反映了其图象是两支,且在范围内向两方无限延伸.
(2)双曲线既是中心对称图形,又是轴对称图形,(0,0)为对称中心,坐标轴为对称轴.
(3) 双曲线的离心率e=反映了双曲线开口的大小,e越大,双曲线的开口就越大.
(4) 双曲线的渐近线是两条直线,当x,y趋向于无穷大时,双曲线将无限地与渐近线接近,但永远没有交点.
本课小结
对双曲线的几何性质的四点说明
本课小结
双曲线与椭圆的六点不同
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实轴、虚轴 长轴、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0
通过本节课,你学会了什么?
