人教版(2019)数学选择性必修第一册期中复习:直线的倾斜角、斜率和直线方程 课件(共25张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修第一册期中复习:直线的倾斜角、斜率和直线方程 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 873.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
直线的倾斜角、斜率和直线方程
新课程标准 考向预测 1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素. 2.理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点的直线斜率的计算公式. 3.确定直线位置的几何要素,探索并掌握直线方程的几种形式(点斜式、两点式及一般式). 命题角度 1.直线的倾斜角与斜率
2.直线的方程
3.直线方程的综合问题
核心素养 数学运算
基础梳理
基础点一 直线的倾斜角和斜率
当直线l与x轴相交时,取x轴作为基准,x轴________与直线l____________之间所成的角叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为________.
直线l的倾斜角α的范围是______________.
①定义
②范围
直线的倾斜角
正方向
向上方向
0°
0°≤α<180°
斜率公式
一条直线的倾斜角α的________叫做这条直线的斜率,斜率常用小写字母k表示,即k=________,倾斜角是________的直线的斜率不存在.
①定义式
经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式k=________.
②坐标式
正切值
tan α
90°
直线都有倾斜角,但不一定都有斜率,
二者的关系具体如下:
倾斜角α 锐角 0° 钝角 90°
斜率k k=tan α>0 k=0 k=tan α<0 不存在
易错提示
1.过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为( )
A.1 B.4 C.1或3 D.1或4
基础小测
A
2.直线y=-x+1的倾斜角为( )
A.30° B.60° C.120° D.150°
C
3.已知A(3,5),B(4,7),C(-1,x)三点共线,则x=________.
-3
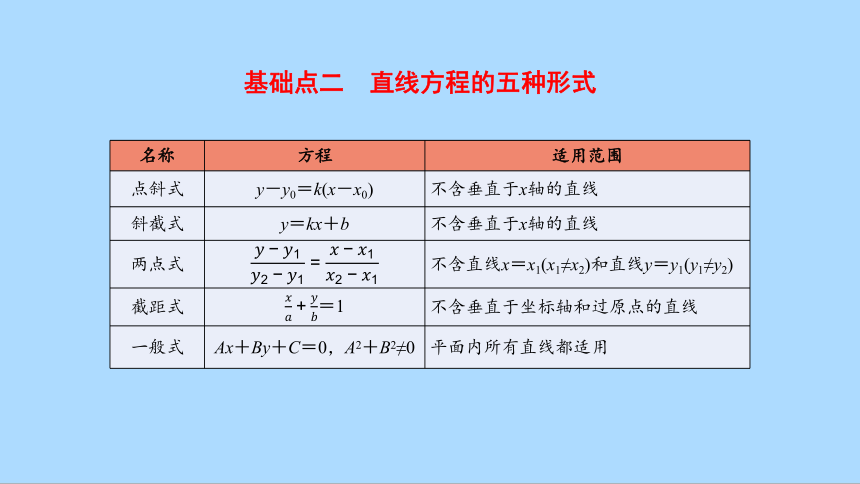
基础点二 直线方程的五种形式
名称 方程 适用范围
点斜式 y-y0=k(x-x0) 不含垂直于x轴的直线
斜截式 y=kx+b 不含垂直于x轴的直线
两点式 不含直线x=x1(x1≠x2)和直线y=y1(y1≠y2)
截距式 =1 不含垂直于坐标轴和过原点的直线
一般式 Ax+By+C=0,A2+B2≠0 平面内所有直线都适用
基础小测
1.已知直线l经过点P(-2,5),且斜率为-,则直线l的方程为( )
A.3x+4y-14=0 B.3x-4y+14=0
C.4x+3y-14=0 D.4x-3y+14=0
A
2.如果A·C<0,且B·C<0,那么直线Ax+By+C=0不通过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
考点突破
考点一 直线的倾斜角和斜率(高考热度:★)
[例1]直线l过点P(1,0),且与以A(2,1),B(0, )为端点的线段有公共点,则直线l斜率的取值范围是__________________________.
(-∞,-]∪[1,+∞)
已知点A(2,-3),B(3,2),直线ax-y-2=0与线段AB相交,则实数a的取值范围是( )
A.-≤a≤ B.a≥ 或a≤-
C.- ≤a≤ D.a≥ 或a≤-
对点变式
C
直线倾斜角的范围是[0,π),而这个区间不是正切函数的单调区间,因此,根据斜率求倾斜角的范围时,要分与两种情况讨论.
易错提醒
直线x+(a2+1)y+1=0的倾斜角的取值范围是( )
A. B.
C. ∪ D. ∪
B
考点微练
考点二 求直线的方程(高考热度:★★)
[例2] 求适合下列条件的直线的方程:
(1)在y轴上的截距为-5,倾斜角的正弦值是;
(2)经过点P(3,2),且在两坐标轴上的截距相等;
(3)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍.
直接法 根据已知条件,选择适当的直线方程形式,直接写出直线方程
待定系数法 ①设所求直线方程的某种形式;
②由条件建立所求参数的方程(组);
③解这个方程(组)求出参数;
④把参数的值代入所设直线方程
求解直线方程的2种方法
方法总结
易错提醒
(1)应用“点斜式”和“斜截式”方程时,要注意讨论斜率是否存在.
(2)应用“截距式”方程时要注意讨论直线是否过原点,截距是否为0.
(3)应用一般式Ax+By+C=0确定直线的斜率时注意讨论B是否为0.
谨防3种失误
考点微练
1.已知直线l的倾斜角为θ且过点(,1),其中sin(θ-)=,则直线l的方程为( )
A. x-y-2=0 B. x+y-4=0
C.x-y=0 D. x+3y-6=0
B
2.经过点A(-5,2),且在x轴上的截距等于在y轴上截距的2倍的直线方程为____________________.
2x+5y=0或x+2y+1=0
3.过A(2,1),B(m,3)两点的直线l的方程为__________________________.
2x-(m-2)y+m-6=0
考点三 直线方程的综合问题(高考热度:★★★)
[例3] 过点P(4,1)作直线l分别交x轴,y轴正半轴于A,B两点,O为坐标原点.
(1)当△AOB面积最小时,求直线l的方程.
(2)当|OA|+|OB|取最小值时,求直线l的方程.
(1)求解与直线方程有关的最值问题.
先设出直线方程,建立目标函数,再利用基本不等式求解最值.
(2)求直线方程.
弄清确定直线的两个条件,由直线方程的几种特殊形式直接写出方程.
(3)求参数值或范围.
注意点在直线上,则点的坐标适合直线的方程,再结合函数的性质或基本不等式求解.
与直线方程有关问题的常见类型及解题策略
解题策略
数学家欧拉在1765年提出定理,三角形的外心、重心、垂心(外心是三角形三条边的垂直平分线的交点,重心是三角形三条中线的交点,垂心是三角形三条高线的交点)依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.已知△ABC的顶点B(-1,0),C(0,2),AB=AC,则△ABC的欧拉线方程为( )
A.2x-4y-3=0 B.2x+4y+3=0
C.4x-2y-3=0 D.2x+4y-3=0
考点微练
D
解析过程见配套学案
通过本节课,你学会了什么?
直线的倾斜角、斜率和直线方程
新课程标准 考向预测 1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素. 2.理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点的直线斜率的计算公式. 3.确定直线位置的几何要素,探索并掌握直线方程的几种形式(点斜式、两点式及一般式). 命题角度 1.直线的倾斜角与斜率
2.直线的方程
3.直线方程的综合问题
核心素养 数学运算
基础梳理
基础点一 直线的倾斜角和斜率
当直线l与x轴相交时,取x轴作为基准,x轴________与直线l____________之间所成的角叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为________.
直线l的倾斜角α的范围是______________.
①定义
②范围
直线的倾斜角
正方向
向上方向
0°
0°≤α<180°
斜率公式
一条直线的倾斜角α的________叫做这条直线的斜率,斜率常用小写字母k表示,即k=________,倾斜角是________的直线的斜率不存在.
①定义式
经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式k=________.
②坐标式
正切值
tan α
90°
直线都有倾斜角,但不一定都有斜率,
二者的关系具体如下:
倾斜角α 锐角 0° 钝角 90°
斜率k k=tan α>0 k=0 k=tan α<0 不存在
易错提示
1.过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为( )
A.1 B.4 C.1或3 D.1或4
基础小测
A
2.直线y=-x+1的倾斜角为( )
A.30° B.60° C.120° D.150°
C
3.已知A(3,5),B(4,7),C(-1,x)三点共线,则x=________.
-3
基础点二 直线方程的五种形式
名称 方程 适用范围
点斜式 y-y0=k(x-x0) 不含垂直于x轴的直线
斜截式 y=kx+b 不含垂直于x轴的直线
两点式 不含直线x=x1(x1≠x2)和直线y=y1(y1≠y2)
截距式 =1 不含垂直于坐标轴和过原点的直线
一般式 Ax+By+C=0,A2+B2≠0 平面内所有直线都适用
基础小测
1.已知直线l经过点P(-2,5),且斜率为-,则直线l的方程为( )
A.3x+4y-14=0 B.3x-4y+14=0
C.4x+3y-14=0 D.4x-3y+14=0
A
2.如果A·C<0,且B·C<0,那么直线Ax+By+C=0不通过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
考点突破
考点一 直线的倾斜角和斜率(高考热度:★)
[例1]直线l过点P(1,0),且与以A(2,1),B(0, )为端点的线段有公共点,则直线l斜率的取值范围是__________________________.
(-∞,-]∪[1,+∞)
已知点A(2,-3),B(3,2),直线ax-y-2=0与线段AB相交,则实数a的取值范围是( )
A.-≤a≤ B.a≥ 或a≤-
C.- ≤a≤ D.a≥ 或a≤-
对点变式
C
直线倾斜角的范围是[0,π),而这个区间不是正切函数的单调区间,因此,根据斜率求倾斜角的范围时,要分与两种情况讨论.
易错提醒
直线x+(a2+1)y+1=0的倾斜角的取值范围是( )
A. B.
C. ∪ D. ∪
B
考点微练
考点二 求直线的方程(高考热度:★★)
[例2] 求适合下列条件的直线的方程:
(1)在y轴上的截距为-5,倾斜角的正弦值是;
(2)经过点P(3,2),且在两坐标轴上的截距相等;
(3)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍.
直接法 根据已知条件,选择适当的直线方程形式,直接写出直线方程
待定系数法 ①设所求直线方程的某种形式;
②由条件建立所求参数的方程(组);
③解这个方程(组)求出参数;
④把参数的值代入所设直线方程
求解直线方程的2种方法
方法总结
易错提醒
(1)应用“点斜式”和“斜截式”方程时,要注意讨论斜率是否存在.
(2)应用“截距式”方程时要注意讨论直线是否过原点,截距是否为0.
(3)应用一般式Ax+By+C=0确定直线的斜率时注意讨论B是否为0.
谨防3种失误
考点微练
1.已知直线l的倾斜角为θ且过点(,1),其中sin(θ-)=,则直线l的方程为( )
A. x-y-2=0 B. x+y-4=0
C.x-y=0 D. x+3y-6=0
B
2.经过点A(-5,2),且在x轴上的截距等于在y轴上截距的2倍的直线方程为____________________.
2x+5y=0或x+2y+1=0
3.过A(2,1),B(m,3)两点的直线l的方程为__________________________.
2x-(m-2)y+m-6=0
考点三 直线方程的综合问题(高考热度:★★★)
[例3] 过点P(4,1)作直线l分别交x轴,y轴正半轴于A,B两点,O为坐标原点.
(1)当△AOB面积最小时,求直线l的方程.
(2)当|OA|+|OB|取最小值时,求直线l的方程.
(1)求解与直线方程有关的最值问题.
先设出直线方程,建立目标函数,再利用基本不等式求解最值.
(2)求直线方程.
弄清确定直线的两个条件,由直线方程的几种特殊形式直接写出方程.
(3)求参数值或范围.
注意点在直线上,则点的坐标适合直线的方程,再结合函数的性质或基本不等式求解.
与直线方程有关问题的常见类型及解题策略
解题策略
数学家欧拉在1765年提出定理,三角形的外心、重心、垂心(外心是三角形三条边的垂直平分线的交点,重心是三角形三条中线的交点,垂心是三角形三条高线的交点)依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.已知△ABC的顶点B(-1,0),C(0,2),AB=AC,则△ABC的欧拉线方程为( )
A.2x-4y-3=0 B.2x+4y+3=0
C.4x-2y-3=0 D.2x+4y-3=0
考点微练
D
解析过程见配套学案
通过本节课,你学会了什么?
同课章节目录
