人教版(2019)数学选择性必修第一册专题:第一章 空间向量与立体几何 课件(共42张PPT)
文档属性
| 名称 | 人教版(2019)数学选择性必修第一册专题:第一章 空间向量与立体几何 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 14:20:57 | ||
图片预览








文档简介
(共42张PPT)
空间向量与立体几何
高二
选修一
本节目录
利用空间向量求线线角、线面角
1
利用空间向量求二面角
2
利用空间向量解决空间角的综合问题
3
考向一 利用空间向量求线线角、线面角
经典再现
例1 (课标全国Ⅲ,16,5分)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时, AB与b成30°角;
②当直线AB与a成60°角时, AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是 .(填写所有正确结论的编号)
②
③
过点C作直线a1∥a,b1∥b,则直线AC、a1、b1两两垂直.不妨分别以a1、b1、AC所在直线为x、y、z轴建立空间直角坐标系,取n1=(1,0,0)为a1的方向向量,n2=(0,1,0)为b1的方向向量,令A(0,0,1).可设B(cos θ,sin θ,0),则=(cos θ,sin θ,-1).
当直线AB与a成60°角时,|cos|= , ∴|cos θ|= , |sin θ|= ,
∴|cos|= ,即AB与b所成角也是60°.
∵|cos|= = ≤ ,
∴直线AB与a所成角的最小值为45°.
综上,②和③是正确的,①和④是错误的.
解法一
过点B作a1∥a, b1∥b,
当直线AB与a成60°角时,由题意,可知AB在由a1,b1确定的平面上的射影为BC,且BC与a1成45°角,又a⊥b,故AB与b所成角也是60°.①错误,②正确;
当直线a∥BC时, AB与a所成角最小, 故最小角为45°.③正确,④错误.
综上,正确的是②③,错误的是①④.
(注:一条斜线与平面所成角的余弦值和其在平面内的射影与平面内一条直线所成角的余弦值的乘积等于斜线和平面内的直线所成角的余弦值)
解法二
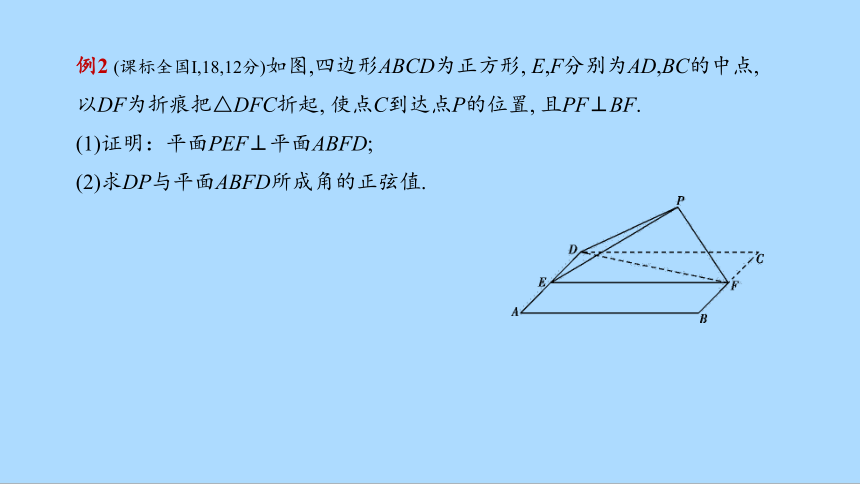
例2 (课标全国Ⅰ,18,12分)如图,四边形ABCD为正方形, E,F分别为AD,BC的中点, 以DF为折痕把△DFC折起, 使点C到达点P的位置, 且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.
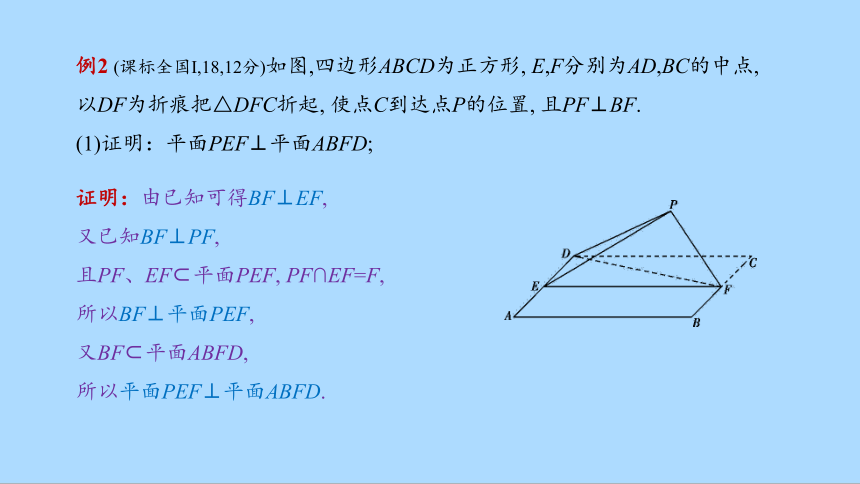
例2 (课标全国Ⅰ,18,12分)如图,四边形ABCD为正方形, E,F分别为AD,BC的中点, 以DF为折痕把△DFC折起, 使点C到达点P的位置, 且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
证明:由已知可得BF⊥EF,
又已知BF⊥PF,
且PF、EF 平面PEF, PF∩EF=F,
所以BF⊥平面PEF,
又BF 平面ABFD,
所以平面PEF⊥平面ABFD.
例2 (课标全国Ⅰ,18,12分)如图,四边形ABCD为正方形, E,F分别为AD,BC的中点, 以DF为折痕把△DFC折起, 使点C到达点P的位置, 且PF⊥BF.
(2)求DP与平面ABFD所成角的正弦值.
作PH⊥EF,垂足为H.由(1)得, PH⊥平面ABFD.
以H为坐标原点, 的方向为y轴正方向, | |为单位长, 建立如图所示的空间直角坐标系H-xyz.
由(1)可得, DE⊥PE.又DP=2, DE=1, 所以PE= ,
又PF=1, EF=2, 故PE⊥PF, 可得PH= , EH= ,
则H(0,0,0), P, D, = , = 为平面ABFD的法向量.
设DP与平面ABFD所成角为θ,则sin θ= = = .
所以DP与平面ABFD所成角的正弦值为.
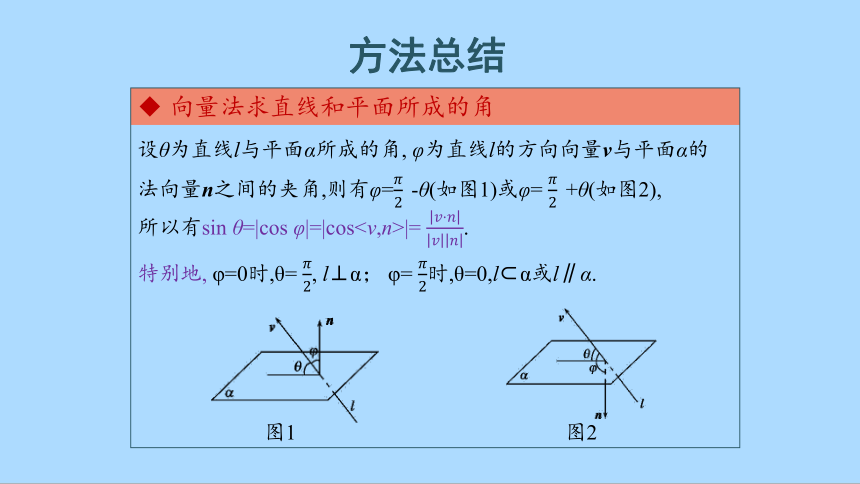
设θ为直线l与平面α所成的角, φ为直线l的方向向量v与平面α的法向量n之间的夹角,则有φ=-θ(如图1)或φ= +θ(如图2),
所以有sin θ=|cos φ|=|cos|= .
特别地, φ=0时,θ= , l⊥α; φ= 时,θ=0,l α或l∥α.
图1 图2
向量法求直线和平面所成的角
方法总结
对点训练
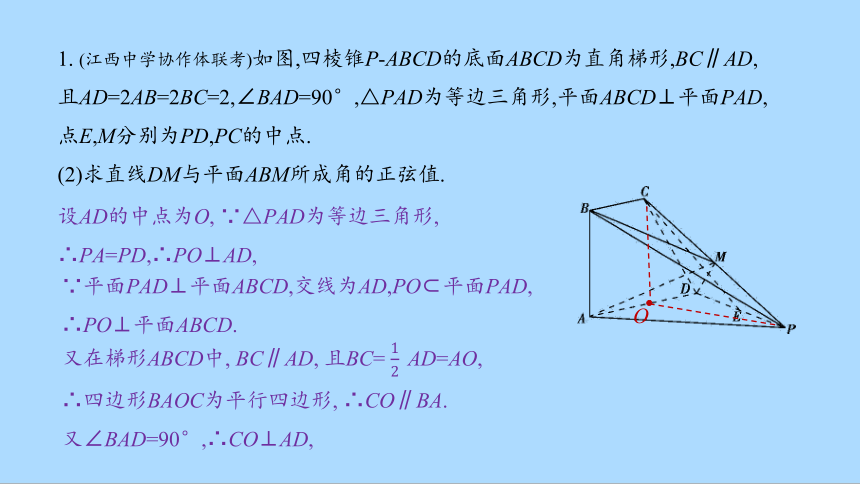
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(1)证明:CE∥平面PAB;
(2)求直线DM与平面ABM所成角的正弦值.
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(1)证明:CE∥平面PAB;
∵E,N分别为PD,PA的中点,
∴EN为△PAD的中位线,∴EN∥AD,且EN= AD.
在梯形ABCD中,BC∥AD,且BC= AD,
∴BC∥EN,BC=EN,∴四边形ENBC是平行四边形,
∴EC∥BN.又BN 平面PAB,CE 平面PAB,∴CE∥平面PAB.
N
证明:设PA的中点为N,连接EN,BN.
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(2)求直线DM与平面ABM所成角的正弦值.
设AD的中点为O, ∵△PAD为等边三角形,
∴PA=PD,∴PO⊥AD,
∵平面PAD⊥平面ABCD,交线为AD,PO 平面PAD,
∴PO⊥平面ABCD.
又在梯形ABCD中, BC∥AD, 且BC= AD=AO,
∴四边形BAOC为平行四边形, ∴CO∥BA.
又∠BAD=90°,∴CO⊥AD,
O
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(2)求直线DM与平面ABM所成角的正弦值.
∴有OA,OC,OP两两垂直,故以点O为坐标原点,OA,OP,OC所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则A(1,0,0), B(1,0,1), C(0,0,1), P(0, ,0), M , D(-1,0,0),
∴ =(0,0,1), = ,
设平面ABM的法向量为m=(x,y,z).则有
令x= ,得y=2,则m=(,2,0).
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(2)求直线DM与平面ABM所成角的正弦值.
由= ,
可得cos=
= = ,
∴直线DM与平面ABM所成角的正弦值为.
2. (四川石室中学模拟)如图,在四棱锥E-ABCD中, 底面ABCD为菱形, 已知∠DAB=∠EAB=60°, AD=AE=2, DE= .
(1)求证:平面ABE⊥平面ABCD;
(2)求直线AE与平面CED所成角的正弦值.
2. (四川石室中学模拟)如图,在四棱锥E-ABCD中, 底面ABCD为菱形, 已知∠DAB=∠EAB=60°, AD=AE=2, DE= .
(1)求证:平面ABE⊥平面ABCD;
证明:如图,过点D作DO⊥AB于点O,连接EO.
∵∠DAB=∠EAB=60°, AD=AE=2, AO=AO,
∴△DAO≌△EAO. ∴∠DOA=∠EOA=90°,DO=EO= .
又∵DE= , ∴DO2+EO2=DE2,
∴由勾股定理的逆定理得∠DOE=90°,即DO⊥EO.
又∵DO⊥AB, AB∩EO=O, AB 平面ABE, EO 平面ABE,
∴DO⊥平面ABE.
又∵DO 平面ABCD, ∴平面ABE⊥平面ABCD.
2. (四川石室中学模拟)如图,在四棱锥E-ABCD中, 底面ABCD为菱形, 已知∠DAB=∠EAB=60°, AD=AE=2, DE= .
(2)求直线AE与平面CED所成角的正弦值.
由(1)可知DO⊥EO,DO⊥AB,EO⊥AB,如图,以O为坐标原点,OE、OB、OD所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系.
由已知得E(,0,0), A(0,-1,0), D(0,0, ), C(0,2, ),
∴ =(,-2,- ), =(0,-2,0), =(- ,-1,0)
设平面CED的法向量为n=(x1,y1,z1),
则 即
2. (四川石室中学模拟)如图,在四棱锥E-ABCD中, 底面ABCD为菱形, 已知∠DAB=∠EAB=60°, AD=AE=2, DE= .
(2)求直线AE与平面CED所成角的正弦值.
令z1=1,则x1=1, ∴n=(1,0,1).
设直线AE与平面CED所成的角为θ,
则sin θ=|cos|= = ,
则直线AE与平面CED所成角的正弦值为.
考向二 利用空间向量求二面角
经典再现
例3 (课标全国Ⅰ,18,12分)如图, 直四棱柱ABCD-A1B1C1D1的底面是菱形, AA1=4, AB=2,∠BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
(课标全国Ⅰ,18,12分)如图, 直四棱柱ABCD-A1B1C1D1的底面是菱形, AA1=4, AB=2,∠BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
证明:连接B1C, ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME= B1C.
又因为N为A1D的中点,所以ND= A1D.
由题设知A1B1 DC,可得B1CA1D,故ME ND,因此四边形MNDE为平行四边形,MN∥ED.
又MN 平面C1DE,所以MN∥平面C1DE.
(课标全国Ⅰ,18,12分)如图, 直四棱柱ABCD-A1B1C1D1的底面是菱形, AA1=4, AB=2,∠BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(2)求二面角A-MA1-N的正弦值.
由已知可得DE⊥DA.以D为坐标原点, 的方向为x轴正方向,建立如图所示的空间直角坐标系D-xyz,
则A(2,0,0), A1(2,0,4), M(1, ,2), N(1,0,2),
=(0,0,-4), =(-1, ,-2), =(-1,0,-2), =(0,- ,0).
设m=(x,y,z)为平面A1MA的法向量,则
所以,可取m=(,1,0).
(课标全国Ⅰ,18,12分)如图, 直四棱柱ABCD-A1B1C1D1的底面是菱形, AA1=4, AB=2,∠BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(2)求二面角A-MA1-N的正弦值.
设n=(p,q,r)为平面A1MN的法向量,则
所以可取n=(2,0,-1).
于是cos= = = ,
所以二面角A-MA1-N的正弦值为.
设二面角α-l-β的平面角为θ(0≤θ≤π), n1,n2分别为平面α, β的法向量,向量n1,n2
的夹角为ω,则有θ+ω=π(如图1)或θ=ω(如图2),其中cos ω= .
向量法求二面角
方法总结
对点训练
(河北唐山第一次联考)在三棱柱ABC-A1B1C1中, AC⊥BC, O为BC的中点, C1O⊥底面ABC, 点M在线段BB1上, 且C1M⊥BB1.
(1)证明:A1M⊥BB1;
(2)若AC=BC, MB=MB1, 求二面角C-A1M-C1的余弦值.
(河北唐山第一次联考)在三棱柱ABC-A1B1C1中, AC⊥BC, O为BC的中点, C1O⊥底面ABC, 点M在线段BB1上, 且C1M⊥BB1.
(1)证明:A1M⊥BB1;
证明:∵C1O⊥底面ABC, AC 底面ABC,
∴C1O⊥AC.又AC⊥BC, BC∩C1O=O, C1O,BC 平面BCC1B1,
∴AC⊥平面BCC1B1.
∵BB1 平面BCC1B1,
∴AC⊥BB1.
又∵AC∥A1C1,∴A1C1⊥BB1.
又∵C1M⊥BB1, A1C1∩C1M=C1, A1C1,C1M 平面A1C1M,
∴BB1⊥平面A1C1M, 而A1M 平面A1C1M, ∴A1M⊥BB1.
(河北唐山第一次联考)在三棱柱ABC-A1B1C1中, AC⊥BC, O为BC的中点, C1O⊥底面ABC, 点M在线段BB1上, 且C1M⊥BB1.
(2)若AC=BC, MB=MB1, 求二面角C-A1M-C1的余弦值.
连接C1B,以点C为坐标原点,CA、CB所在直线分别为x轴、y轴建立如图所示的空间直角坐标系.
∵MB=MB1,且C1M⊥BB1,∴C1B1=C1B=BC,
又C1O⊥底面ABC, BC 平面ABC,
∴C1O⊥BC, 又O为BC的中点,
∴C1C=C1B=BC,∴△C1CB为等边三角形.
设AC=2,则C(0,0,0),A(2,0,0),B(0,2,0),C1(0,1, ),
(河北唐山第一次联考)在三棱柱ABC-A1B1C1中, AC⊥BC, O为BC的中点, C1O⊥底面ABC, 点M在线段BB1上, 且C1M⊥BB1.
(2)若AC=BC, MB=MB1, 求二面角C-A1M-C1的余弦值.
由(1)可知平面A1MC1的一个法向量为=(0,1, ),
则= + =(2,1, ),= + = + = .
设平面CA1M的法向量为n=(x,y,z),
则
令y= ,则x=2 ,z=-5,∴n=(2 , ,-5).
∴cos< ,n>= = =- .
由图可知二面角C-A1M-C1为锐角, ∴二面角C-A1M-C1的余弦值为.
考向三 利用空间向量解决空间角的综合问题
经典再现
例4 (课标全国Ⅱ,20,12分)如图, 在三棱锥P-ABC中, AB=BC=2, PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,
求PC与平面PAM所成角的正弦值.
例4 (课标全国Ⅱ,20,12分)如图, 在三棱锥P-ABC中, AB=BC=2, PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
连接OB.因为AB=BC= AC,
所以△ABC为等腰直角三角形,
且OB⊥AC,OB= AC=2.
由OP2+OB2=PB2知PO⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
证明:因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=2.
例4 (课标全国Ⅱ,20,12分)如图, 在三棱锥P-ABC中, AB=BC=2, PA=PB=PC=AC=4,O为AC的中点.
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
如图,以O为坐标原点, 的方向为x轴正方向,建立如图所示的空间直角坐标系O-xyz.
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2), =(0,2,2).取平面PAC的法向量=(2,0,0).
设M(a,2-a,0)(0设平面PAM的法向量为n=(x,y,z).
例4 (课标全国Ⅱ,20,12分)如图, 在三棱锥P-ABC中, AB=BC=2, PA=PB=PC=AC=4,O为AC的中点.
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
由·n=0, ·n=0得
可取n=((a-4), a,-a),
所以cos< ,n>= .
由已知可得|cos< ,n>|= .
所以= .解得a=-4(舍去)或a= .
所以n= .又=(0,2,-2 ),所以cos< ,n>= .
所以PC与平面PAM所成角的正弦值为.
例5 (课标全国Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD
是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,
求二面角D-AE-C的余弦值.
例5 (课标全国Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD
是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
证明:由题设可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°.
所以平面ACD⊥平面ABC.
O
例5 (课标全国Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD
是直角三角形,∠ABD=∠CBD,AB=BD.
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,
求二面角D-AE-C的余弦值.
由题设及(1)知,OA,OB,OD两两垂直.以O为坐标原点, 的方向为x轴正方向,| |为单位长,建立如图所示的空间直角坐标系O-xyz.
则A(1,0,0),B(0, ,0),C(-1,0,0),D(0,0,1).
由题设知,四面体ABCE的体积为四面体ABCD的体积的,从而E到平面ABC的距离为D到平面ABC的距离的,
即E为DB的中点,得E .
例5 (课标全国Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD
是直角三角形,∠ABD=∠CBD,AB=BD.
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,
求二面角D-AE-C的余弦值.
故=(-1,0,1), =(-2,0,0), = .
设n=(x,y,z)是平面DAE的法向量,
则即可取n= .
设m是平面AEC的法向量,则, 同理可取m=(0,-1, ).
则cos= = . 易知二面角D-AE-C为锐角,
所以二面角D-AE-C的余弦值为.
总结提升
正确分析空间几何体的特征,建立合适的空间直角坐标系,是解决此类问题的关键.
对点训练
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(1)求证:平面A1CP⊥平面A1BE;
(2)若点M在线段CD上,当直线A1M与平面A1PD所成角的正弦值为时,求二面角M-A1P-D的余弦值.
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(1)求证:平面A1CP⊥平面A1BE;
证明:因为AB=2,AE= AD=2,
所以BE= =4.
又tan∠ABE= = ,所以∠ABE= ,易知∠PBC= .
在△BPC中,BP= BE=2,BC=4,
所以PC= = =2 ,
所以BP2+PC2=BC2,所以BP⊥PC.在△A1PC中,A1P= BE=2,A1C=4,所以A1P2+PC2=A1C2,所以A1P⊥PC.
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(1)求证:平面A1CP⊥平面A1BE;
因为A1P 平面A1BE, PB 平面A1BE,
PB∩A1P=P,所以PC⊥平面A1BE.
又PC 平面A1CP,
所以平面A1CP⊥平面A1BE.
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(2)若点M在线段CD上,当直线A1M与平面A1PD所成角的正弦值为时,求二面角M-A1P-D的余弦值.
以点P为坐标原点, PC,PE所在直线分别为x轴, y轴建立如图所示的空间直角坐标系,
则A1(0,1, ), C(2,0,0), D(2,4,0).
设M(2,a,0), 0≤a≤4,
则=(2,a-1,-), =(0,1, ), =(2,4,0).
设平面A1PD的法向量为m=(x1,y1,z1),
由 得
令x1=2,则y1=, z1=1, 所以m=(2,,1),
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(2)若点M在线段CD上,当直线A1M与平面A1PD所成角的正弦值为时,求二面角M-A1P-D的余弦值.
所以|cos|= = ,
解得a=2或a=8(舍),
所以=(2,1,), =(2,2,0).
设平面A1PM的法向量为n=(x2,y2,z2),
由得
令x2=1,则y2=, z2=1, 所以n=(1,,1),
所以cos= = .
由图可知二面角M-A1P-D为锐角,
∴当直线A1M与平面A1PD所成角的正弦值为时,二面角M-A1P-D的余弦值为.
通过本节课,你学会了什么?
空间向量与立体几何
高二
选修一
本节目录
利用空间向量求线线角、线面角
1
利用空间向量求二面角
2
利用空间向量解决空间角的综合问题
3
考向一 利用空间向量求线线角、线面角
经典再现
例1 (课标全国Ⅲ,16,5分)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时, AB与b成30°角;
②当直线AB与a成60°角时, AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是 .(填写所有正确结论的编号)
②
③
过点C作直线a1∥a,b1∥b,则直线AC、a1、b1两两垂直.不妨分别以a1、b1、AC所在直线为x、y、z轴建立空间直角坐标系,取n1=(1,0,0)为a1的方向向量,n2=(0,1,0)为b1的方向向量,令A(0,0,1).可设B(cos θ,sin θ,0),则=(cos θ,sin θ,-1).
当直线AB与a成60°角时,|cos
∴|cos
∵|cos
∴直线AB与a所成角的最小值为45°.
综上,②和③是正确的,①和④是错误的.
解法一
过点B作a1∥a, b1∥b,
当直线AB与a成60°角时,由题意,可知AB在由a1,b1确定的平面上的射影为BC,且BC与a1成45°角,又a⊥b,故AB与b所成角也是60°.①错误,②正确;
当直线a∥BC时, AB与a所成角最小, 故最小角为45°.③正确,④错误.
综上,正确的是②③,错误的是①④.
(注:一条斜线与平面所成角的余弦值和其在平面内的射影与平面内一条直线所成角的余弦值的乘积等于斜线和平面内的直线所成角的余弦值)
解法二
例2 (课标全国Ⅰ,18,12分)如图,四边形ABCD为正方形, E,F分别为AD,BC的中点, 以DF为折痕把△DFC折起, 使点C到达点P的位置, 且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.
例2 (课标全国Ⅰ,18,12分)如图,四边形ABCD为正方形, E,F分别为AD,BC的中点, 以DF为折痕把△DFC折起, 使点C到达点P的位置, 且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
证明:由已知可得BF⊥EF,
又已知BF⊥PF,
且PF、EF 平面PEF, PF∩EF=F,
所以BF⊥平面PEF,
又BF 平面ABFD,
所以平面PEF⊥平面ABFD.
例2 (课标全国Ⅰ,18,12分)如图,四边形ABCD为正方形, E,F分别为AD,BC的中点, 以DF为折痕把△DFC折起, 使点C到达点P的位置, 且PF⊥BF.
(2)求DP与平面ABFD所成角的正弦值.
作PH⊥EF,垂足为H.由(1)得, PH⊥平面ABFD.
以H为坐标原点, 的方向为y轴正方向, | |为单位长, 建立如图所示的空间直角坐标系H-xyz.
由(1)可得, DE⊥PE.又DP=2, DE=1, 所以PE= ,
又PF=1, EF=2, 故PE⊥PF, 可得PH= , EH= ,
则H(0,0,0), P, D, = , = 为平面ABFD的法向量.
设DP与平面ABFD所成角为θ,则sin θ= = = .
所以DP与平面ABFD所成角的正弦值为.
设θ为直线l与平面α所成的角, φ为直线l的方向向量v与平面α的法向量n之间的夹角,则有φ=-θ(如图1)或φ= +θ(如图2),
所以有sin θ=|cos φ|=|cos
特别地, φ=0时,θ= , l⊥α; φ= 时,θ=0,l α或l∥α.
图1 图2
向量法求直线和平面所成的角
方法总结
对点训练
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(1)证明:CE∥平面PAB;
(2)求直线DM与平面ABM所成角的正弦值.
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(1)证明:CE∥平面PAB;
∵E,N分别为PD,PA的中点,
∴EN为△PAD的中位线,∴EN∥AD,且EN= AD.
在梯形ABCD中,BC∥AD,且BC= AD,
∴BC∥EN,BC=EN,∴四边形ENBC是平行四边形,
∴EC∥BN.又BN 平面PAB,CE 平面PAB,∴CE∥平面PAB.
N
证明:设PA的中点为N,连接EN,BN.
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(2)求直线DM与平面ABM所成角的正弦值.
设AD的中点为O, ∵△PAD为等边三角形,
∴PA=PD,∴PO⊥AD,
∵平面PAD⊥平面ABCD,交线为AD,PO 平面PAD,
∴PO⊥平面ABCD.
又在梯形ABCD中, BC∥AD, 且BC= AD=AO,
∴四边形BAOC为平行四边形, ∴CO∥BA.
又∠BAD=90°,∴CO⊥AD,
O
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(2)求直线DM与平面ABM所成角的正弦值.
∴有OA,OC,OP两两垂直,故以点O为坐标原点,OA,OP,OC所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则A(1,0,0), B(1,0,1), C(0,0,1), P(0, ,0), M , D(-1,0,0),
∴ =(0,0,1), = ,
设平面ABM的法向量为m=(x,y,z).则有
令x= ,得y=2,则m=(,2,0).
1. (江西中学协作体联考)如图,四棱锥P-ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD,点E,M分别为PD,PC的中点.
(2)求直线DM与平面ABM所成角的正弦值.
由= ,
可得cos
= = ,
∴直线DM与平面ABM所成角的正弦值为.
2. (四川石室中学模拟)如图,在四棱锥E-ABCD中, 底面ABCD为菱形, 已知∠DAB=∠EAB=60°, AD=AE=2, DE= .
(1)求证:平面ABE⊥平面ABCD;
(2)求直线AE与平面CED所成角的正弦值.
2. (四川石室中学模拟)如图,在四棱锥E-ABCD中, 底面ABCD为菱形, 已知∠DAB=∠EAB=60°, AD=AE=2, DE= .
(1)求证:平面ABE⊥平面ABCD;
证明:如图,过点D作DO⊥AB于点O,连接EO.
∵∠DAB=∠EAB=60°, AD=AE=2, AO=AO,
∴△DAO≌△EAO. ∴∠DOA=∠EOA=90°,DO=EO= .
又∵DE= , ∴DO2+EO2=DE2,
∴由勾股定理的逆定理得∠DOE=90°,即DO⊥EO.
又∵DO⊥AB, AB∩EO=O, AB 平面ABE, EO 平面ABE,
∴DO⊥平面ABE.
又∵DO 平面ABCD, ∴平面ABE⊥平面ABCD.
2. (四川石室中学模拟)如图,在四棱锥E-ABCD中, 底面ABCD为菱形, 已知∠DAB=∠EAB=60°, AD=AE=2, DE= .
(2)求直线AE与平面CED所成角的正弦值.
由(1)可知DO⊥EO,DO⊥AB,EO⊥AB,如图,以O为坐标原点,OE、OB、OD所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系.
由已知得E(,0,0), A(0,-1,0), D(0,0, ), C(0,2, ),
∴ =(,-2,- ), =(0,-2,0), =(- ,-1,0)
设平面CED的法向量为n=(x1,y1,z1),
则 即
2. (四川石室中学模拟)如图,在四棱锥E-ABCD中, 底面ABCD为菱形, 已知∠DAB=∠EAB=60°, AD=AE=2, DE= .
(2)求直线AE与平面CED所成角的正弦值.
令z1=1,则x1=1, ∴n=(1,0,1).
设直线AE与平面CED所成的角为θ,
则sin θ=|cos
则直线AE与平面CED所成角的正弦值为.
考向二 利用空间向量求二面角
经典再现
例3 (课标全国Ⅰ,18,12分)如图, 直四棱柱ABCD-A1B1C1D1的底面是菱形, AA1=4, AB=2,∠BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
(课标全国Ⅰ,18,12分)如图, 直四棱柱ABCD-A1B1C1D1的底面是菱形, AA1=4, AB=2,∠BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
证明:连接B1C, ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME= B1C.
又因为N为A1D的中点,所以ND= A1D.
由题设知A1B1 DC,可得B1CA1D,故ME ND,因此四边形MNDE为平行四边形,MN∥ED.
又MN 平面C1DE,所以MN∥平面C1DE.
(课标全国Ⅰ,18,12分)如图, 直四棱柱ABCD-A1B1C1D1的底面是菱形, AA1=4, AB=2,∠BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(2)求二面角A-MA1-N的正弦值.
由已知可得DE⊥DA.以D为坐标原点, 的方向为x轴正方向,建立如图所示的空间直角坐标系D-xyz,
则A(2,0,0), A1(2,0,4), M(1, ,2), N(1,0,2),
=(0,0,-4), =(-1, ,-2), =(-1,0,-2), =(0,- ,0).
设m=(x,y,z)为平面A1MA的法向量,则
所以,可取m=(,1,0).
(课标全国Ⅰ,18,12分)如图, 直四棱柱ABCD-A1B1C1D1的底面是菱形, AA1=4, AB=2,∠BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(2)求二面角A-MA1-N的正弦值.
设n=(p,q,r)为平面A1MN的法向量,则
所以可取n=(2,0,-1).
于是cos
所以二面角A-MA1-N的正弦值为.
设二面角α-l-β的平面角为θ(0≤θ≤π), n1,n2分别为平面α, β的法向量,向量n1,n2
的夹角为ω,则有θ+ω=π(如图1)或θ=ω(如图2),其中cos ω= .
向量法求二面角
方法总结
对点训练
(河北唐山第一次联考)在三棱柱ABC-A1B1C1中, AC⊥BC, O为BC的中点, C1O⊥底面ABC, 点M在线段BB1上, 且C1M⊥BB1.
(1)证明:A1M⊥BB1;
(2)若AC=BC, MB=MB1, 求二面角C-A1M-C1的余弦值.
(河北唐山第一次联考)在三棱柱ABC-A1B1C1中, AC⊥BC, O为BC的中点, C1O⊥底面ABC, 点M在线段BB1上, 且C1M⊥BB1.
(1)证明:A1M⊥BB1;
证明:∵C1O⊥底面ABC, AC 底面ABC,
∴C1O⊥AC.又AC⊥BC, BC∩C1O=O, C1O,BC 平面BCC1B1,
∴AC⊥平面BCC1B1.
∵BB1 平面BCC1B1,
∴AC⊥BB1.
又∵AC∥A1C1,∴A1C1⊥BB1.
又∵C1M⊥BB1, A1C1∩C1M=C1, A1C1,C1M 平面A1C1M,
∴BB1⊥平面A1C1M, 而A1M 平面A1C1M, ∴A1M⊥BB1.
(河北唐山第一次联考)在三棱柱ABC-A1B1C1中, AC⊥BC, O为BC的中点, C1O⊥底面ABC, 点M在线段BB1上, 且C1M⊥BB1.
(2)若AC=BC, MB=MB1, 求二面角C-A1M-C1的余弦值.
连接C1B,以点C为坐标原点,CA、CB所在直线分别为x轴、y轴建立如图所示的空间直角坐标系.
∵MB=MB1,且C1M⊥BB1,∴C1B1=C1B=BC,
又C1O⊥底面ABC, BC 平面ABC,
∴C1O⊥BC, 又O为BC的中点,
∴C1C=C1B=BC,∴△C1CB为等边三角形.
设AC=2,则C(0,0,0),A(2,0,0),B(0,2,0),C1(0,1, ),
(河北唐山第一次联考)在三棱柱ABC-A1B1C1中, AC⊥BC, O为BC的中点, C1O⊥底面ABC, 点M在线段BB1上, 且C1M⊥BB1.
(2)若AC=BC, MB=MB1, 求二面角C-A1M-C1的余弦值.
由(1)可知平面A1MC1的一个法向量为=(0,1, ),
则= + =(2,1, ),= + = + = .
设平面CA1M的法向量为n=(x,y,z),
则
令y= ,则x=2 ,z=-5,∴n=(2 , ,-5).
∴cos< ,n>= = =- .
由图可知二面角C-A1M-C1为锐角, ∴二面角C-A1M-C1的余弦值为.
考向三 利用空间向量解决空间角的综合问题
经典再现
例4 (课标全国Ⅱ,20,12分)如图, 在三棱锥P-ABC中, AB=BC=2, PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,
求PC与平面PAM所成角的正弦值.
例4 (课标全国Ⅱ,20,12分)如图, 在三棱锥P-ABC中, AB=BC=2, PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
连接OB.因为AB=BC= AC,
所以△ABC为等腰直角三角形,
且OB⊥AC,OB= AC=2.
由OP2+OB2=PB2知PO⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
证明:因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=2.
例4 (课标全国Ⅱ,20,12分)如图, 在三棱锥P-ABC中, AB=BC=2, PA=PB=PC=AC=4,O为AC的中点.
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
如图,以O为坐标原点, 的方向为x轴正方向,建立如图所示的空间直角坐标系O-xyz.
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2), =(0,2,2).取平面PAC的法向量=(2,0,0).
设M(a,2-a,0)(0
例4 (课标全国Ⅱ,20,12分)如图, 在三棱锥P-ABC中, AB=BC=2, PA=PB=PC=AC=4,O为AC的中点.
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
由·n=0, ·n=0得
可取n=((a-4), a,-a),
所以cos< ,n>= .
由已知可得|cos< ,n>|= .
所以= .解得a=-4(舍去)或a= .
所以n= .又=(0,2,-2 ),所以cos< ,n>= .
所以PC与平面PAM所成角的正弦值为.
例5 (课标全国Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD
是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,
求二面角D-AE-C的余弦值.
例5 (课标全国Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD
是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
证明:由题设可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°.
所以平面ACD⊥平面ABC.
O
例5 (课标全国Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD
是直角三角形,∠ABD=∠CBD,AB=BD.
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,
求二面角D-AE-C的余弦值.
由题设及(1)知,OA,OB,OD两两垂直.以O为坐标原点, 的方向为x轴正方向,| |为单位长,建立如图所示的空间直角坐标系O-xyz.
则A(1,0,0),B(0, ,0),C(-1,0,0),D(0,0,1).
由题设知,四面体ABCE的体积为四面体ABCD的体积的,从而E到平面ABC的距离为D到平面ABC的距离的,
即E为DB的中点,得E .
例5 (课标全国Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD
是直角三角形,∠ABD=∠CBD,AB=BD.
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,
求二面角D-AE-C的余弦值.
故=(-1,0,1), =(-2,0,0), = .
设n=(x,y,z)是平面DAE的法向量,
则即可取n= .
设m是平面AEC的法向量,则, 同理可取m=(0,-1, ).
则cos
所以二面角D-AE-C的余弦值为.
总结提升
正确分析空间几何体的特征,建立合适的空间直角坐标系,是解决此类问题的关键.
对点训练
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(1)求证:平面A1CP⊥平面A1BE;
(2)若点M在线段CD上,当直线A1M与平面A1PD所成角的正弦值为时,求二面角M-A1P-D的余弦值.
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(1)求证:平面A1CP⊥平面A1BE;
证明:因为AB=2,AE= AD=2,
所以BE= =4.
又tan∠ABE= = ,所以∠ABE= ,易知∠PBC= .
在△BPC中,BP= BE=2,BC=4,
所以PC= = =2 ,
所以BP2+PC2=BC2,所以BP⊥PC.在△A1PC中,A1P= BE=2,A1C=4,所以A1P2+PC2=A1C2,所以A1P⊥PC.
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(1)求证:平面A1CP⊥平面A1BE;
因为A1P 平面A1BE, PB 平面A1BE,
PB∩A1P=P,所以PC⊥平面A1BE.
又PC 平面A1CP,
所以平面A1CP⊥平面A1BE.
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(2)若点M在线段CD上,当直线A1M与平面A1PD所成角的正弦值为时,求二面角M-A1P-D的余弦值.
以点P为坐标原点, PC,PE所在直线分别为x轴, y轴建立如图所示的空间直角坐标系,
则A1(0,1, ), C(2,0,0), D(2,4,0).
设M(2,a,0), 0≤a≤4,
则=(2,a-1,-), =(0,1, ), =(2,4,0).
设平面A1PD的法向量为m=(x1,y1,z1),
由 得
令x1=2,则y1=, z1=1, 所以m=(2,,1),
(黑龙江哈尔滨第三中学模拟)如图①,在四边形ABCD中, AD∥BC,∠BAD=90°, AB=2,BC=4,AD=6,E是AD上的点,且AE= AD,P为BE的中点.
将△ABE沿BE折到△A1BE的位置,使得A1C=4,如图②.
(2)若点M在线段CD上,当直线A1M与平面A1PD所成角的正弦值为时,求二面角M-A1P-D的余弦值.
所以|cos
解得a=2或a=8(舍),
所以=(2,1,), =(2,2,0).
设平面A1PM的法向量为n=(x2,y2,z2),
由得
令x2=1,则y2=, z2=1, 所以n=(1,,1),
所以cos
由图可知二面角M-A1P-D为锐角,
∴当直线A1M与平面A1PD所成角的正弦值为时,二面角M-A1P-D的余弦值为.
通过本节课,你学会了什么?
