人教版数学七年级上册 1.5.1 乘方-第1课时 有理数的乘方 课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级上册 1.5.1 乘方-第1课时 有理数的乘方 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 396.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 12:14:09 | ||
图片预览







文档简介
(共22张PPT)
第 一 章 有理数
数学 七年级 上册 R
1.5 有理数的乘方
1.5.1 乘方
第1课时 有理数的乘方
大家都见过拉面师傅拉面,一次小明看到拉面师傅拉了6次,一碗面就拉好了,你能列出算式,帮他算算这碗面共有多少根吗?这个问题就是这节课我们要学习的乘方.
新课导入
学习目标:
1.知道有理数乘方的意义,能说出乘方运算、
幂、底数、指数等概念.
2.能正确进行有理数乘方运算.
学习重、难点:
重点:知道有理数乘方的意义.
难点:能合理地进行乘方运算.
乘方的定义
知识点1
1次
2次
20次
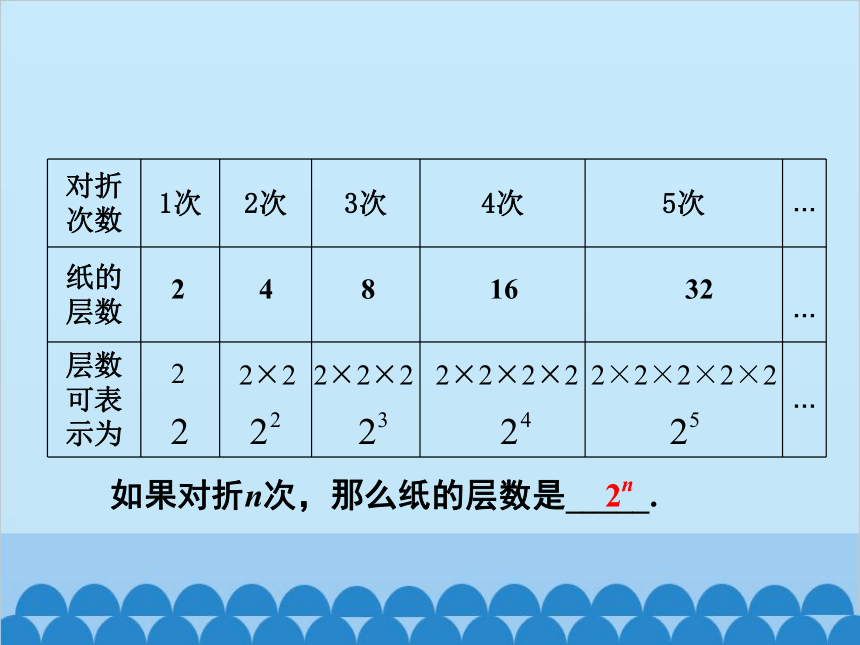
做一做:请同学们把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
新课推进
2
4
8
16
32
如果对折n次,那么纸的层数是_____.
2n
对折
次数 1次 2次 3次 4次 5次 …
纸的
层数
…
层数可表示为 …
2
2×2×2
2×2×2×2
2×2×2×2×2
2×2
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作 ,读作
a的n次方.
n个
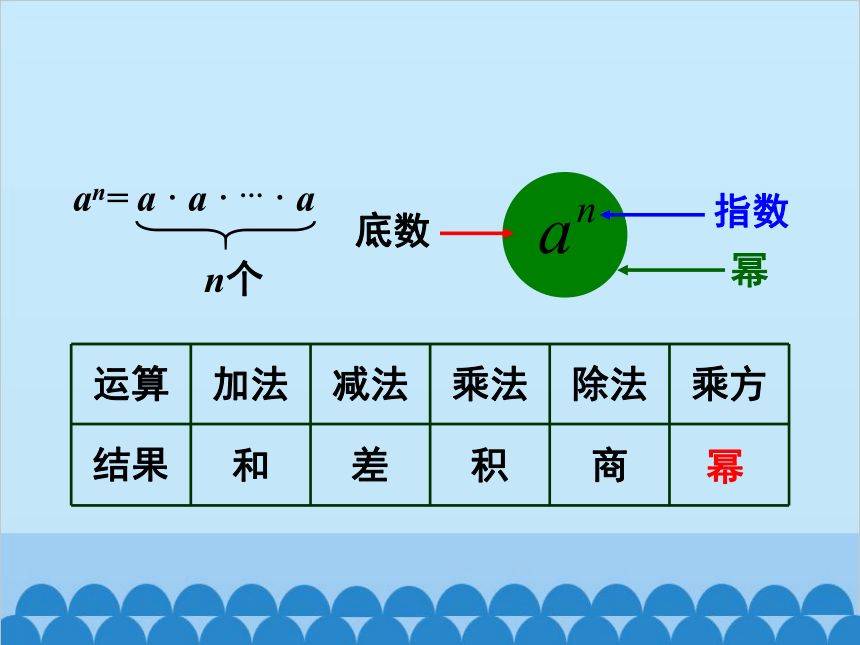
a · a · … · a
底数
指数
幂
运算 加法 减法 乘法 除法 乘方
结果 和 差 积 商
幂
n个
an= a · a · … · a
例1 说出下列乘方的底数、指数且计算:
(1) (-4)3; (2) (-2)4;
(3) 07; (4) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
例1 说出下列乘方的底数、指数且计算:
(1) (-4)3; (2) (-2)4;
(3) 07; (4) .
(3) 07 =0×0×0×0 × 0×0×0=0;
解:
(4)
1.在(-2)5中,底数是 ,指数是 ,结果是 .
-2
5
-32
2.在-24中,底数是 ,指数是 ,结果是 .
2
4
-16
强化训练
乘方的符号法则
知识点2
计算:102 , 103 , 104.
解:(1)102
=10×10 =
100;
103 =
10 ×10×10
= 1 000;
(2)
104 =
10 ×10×10 ×10
=10 000.
(3)
答:10的几次方,幂的结果中1后面就有几个0.
观察结果,你能发现什么规律?
想一想:
(1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法;
(2)分数的乘方,在书写时一定要把整个分数用小括号括起来.
由上题中
你有什么发现?
和
探究1
探究2
不计算下列各式,你能确定其结果的符号吗?从计算结果中,你能得到什么规律?
⑴(-2)51; ⑵(-2)50; ⑶250; ⑷251;
⑸(-1)2012;⑹(-1)2013;⑺02012;⑻12013.
归纳
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂
是负数;
(3)0的任何次幂等于零;
(4)1的任何次幂等于1;
(5)-1的偶次幂等于1;-1的奇次幂是-1.
乘方运算的
符号规律
你能用计算器计算 和 吗?
你能迅速判断下列各幂的正负吗?
正
正
负
正
负
正
强化训练
(1)23中底数是 ,指数是 ,幂是 .
(2) 中底数是 ,指数是 ,幂是 .
(3)(-5)4中底数是 ,指数是 ,幂是 .
(4) 中底数是 ,指数是 ,结果是 .
2
3
2
-5
4
625
8
1.回答下列问题:
5
4
-625
随堂练习
(3)-32=(-3)2. ( )
(4) ( )
(5) ( )
2.判断正误:(对的画“√”,错的画“×”)
(1)32 =3×2=6. ( )
(2)(-2)3=(-3)2. ( )
×
×
×
×
×
3. (1)计算0.12,12,102,1002,观察这些结果,底数的小数点向左(或右)移动一位时,平方数的小数点有什么移动规律?
(2)计算0.13,13,103,1003,观察这些结果,底数的小数点向左(或右)移动一位时,立方数的小数点有什么移动规律?
解:
(1)平方数的小数点向左(向右)移动2位.
(2)立方数的小数点向左(向右)移动3位.
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作 ,读作
a的n次方.
n个
a · a · … · a
课堂小结
谢谢大家!
第 一 章 有理数
数学 七年级 上册 R
1.5 有理数的乘方
1.5.1 乘方
第1课时 有理数的乘方
大家都见过拉面师傅拉面,一次小明看到拉面师傅拉了6次,一碗面就拉好了,你能列出算式,帮他算算这碗面共有多少根吗?这个问题就是这节课我们要学习的乘方.
新课导入
学习目标:
1.知道有理数乘方的意义,能说出乘方运算、
幂、底数、指数等概念.
2.能正确进行有理数乘方运算.
学习重、难点:
重点:知道有理数乘方的意义.
难点:能合理地进行乘方运算.
乘方的定义
知识点1
1次
2次
20次
做一做:请同学们把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
新课推进
2
4
8
16
32
如果对折n次,那么纸的层数是_____.
2n
对折
次数 1次 2次 3次 4次 5次 …
纸的
层数
…
层数可表示为 …
2
2×2×2
2×2×2×2
2×2×2×2×2
2×2
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作 ,读作
a的n次方.
n个
a · a · … · a
底数
指数
幂
运算 加法 减法 乘法 除法 乘方
结果 和 差 积 商
幂
n个
an= a · a · … · a
例1 说出下列乘方的底数、指数且计算:
(1) (-4)3; (2) (-2)4;
(3) 07; (4) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
例1 说出下列乘方的底数、指数且计算:
(1) (-4)3; (2) (-2)4;
(3) 07; (4) .
(3) 07 =0×0×0×0 × 0×0×0=0;
解:
(4)
1.在(-2)5中,底数是 ,指数是 ,结果是 .
-2
5
-32
2.在-24中,底数是 ,指数是 ,结果是 .
2
4
-16
强化训练
乘方的符号法则
知识点2
计算:102 , 103 , 104.
解:(1)102
=10×10 =
100;
103 =
10 ×10×10
= 1 000;
(2)
104 =
10 ×10×10 ×10
=10 000.
(3)
答:10的几次方,幂的结果中1后面就有几个0.
观察结果,你能发现什么规律?
想一想:
(1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法;
(2)分数的乘方,在书写时一定要把整个分数用小括号括起来.
由上题中
你有什么发现?
和
探究1
探究2
不计算下列各式,你能确定其结果的符号吗?从计算结果中,你能得到什么规律?
⑴(-2)51; ⑵(-2)50; ⑶250; ⑷251;
⑸(-1)2012;⑹(-1)2013;⑺02012;⑻12013.
归纳
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂
是负数;
(3)0的任何次幂等于零;
(4)1的任何次幂等于1;
(5)-1的偶次幂等于1;-1的奇次幂是-1.
乘方运算的
符号规律
你能用计算器计算 和 吗?
你能迅速判断下列各幂的正负吗?
正
正
负
正
负
正
强化训练
(1)23中底数是 ,指数是 ,幂是 .
(2) 中底数是 ,指数是 ,幂是 .
(3)(-5)4中底数是 ,指数是 ,幂是 .
(4) 中底数是 ,指数是 ,结果是 .
2
3
2
-5
4
625
8
1.回答下列问题:
5
4
-625
随堂练习
(3)-32=(-3)2. ( )
(4) ( )
(5) ( )
2.判断正误:(对的画“√”,错的画“×”)
(1)32 =3×2=6. ( )
(2)(-2)3=(-3)2. ( )
×
×
×
×
×
3. (1)计算0.12,12,102,1002,观察这些结果,底数的小数点向左(或右)移动一位时,平方数的小数点有什么移动规律?
(2)计算0.13,13,103,1003,观察这些结果,底数的小数点向左(或右)移动一位时,立方数的小数点有什么移动规律?
解:
(1)平方数的小数点向左(向右)移动2位.
(2)立方数的小数点向左(向右)移动3位.
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作 ,读作
a的n次方.
n个
a · a · … · a
课堂小结
谢谢大家!
