湘教版九上数学3.5相似三角形的应用 课件(共23张PPT)
文档属性
| 名称 | 湘教版九上数学3.5相似三角形的应用 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 21:20:51 | ||
图片预览





文档简介
(共23张PPT)
3.5 相似三角形的应用
湘教版九年级上册
教学目标
1. 能利用相似三角形测量、计算两点间的距离或线段长度.
2. 熟悉构造相似三角形的方法解决现实中的测量问题.
3. 提高分析问题、解决问题的能力.
4. 培养热爱生活的情感,激发学生学习数学的兴趣.
新知讲解
如图3-32,A,B两点分别位于一个池塘的两端,小张想量出A,B间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量方法吗?
新知讲解
我们可以这样做:
如图3-33,在池塘外取一点C,使它可以直接看到AB两点,连接并延长AC,BC,在AC的延长线上取一点D,在BC的
延长线上取一点E,使 (k为正整数),测量出DE的长度后,就可以由相似三角形的有关知识求出A,B两点间的距离了.
合作探究
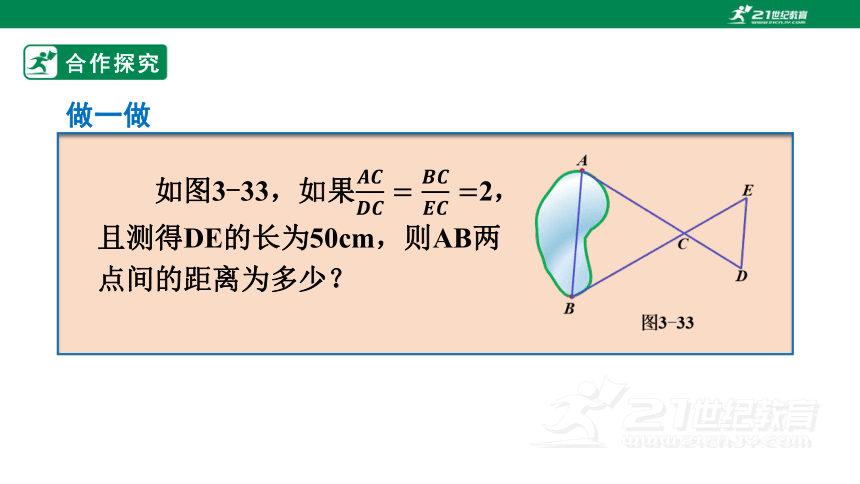
如图3-33,如果2,且测得DE的长为50cm,则AB两点间的距离为多少?
做一做
合作探究
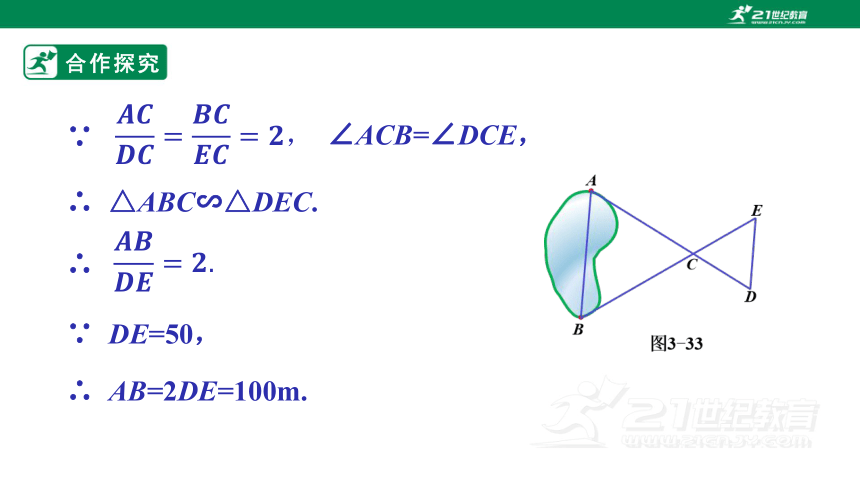
∵
∠ACB=∠DCE,
∴ △ABC∽△DEC.
∴
∵ DE=50,
∴ AB=2DE=100m.
方法小结
在实际生活中,当直接测量两点间的距离比较困难时,可以在容易测量线段长度的某一位置取一点,构造一对相似三角形,从而利用“相似三角形的对应边成比例”即可求得这两点间的距离,如一座小山两侧两个点之间的距离、一条河的宽度等.
合作探究
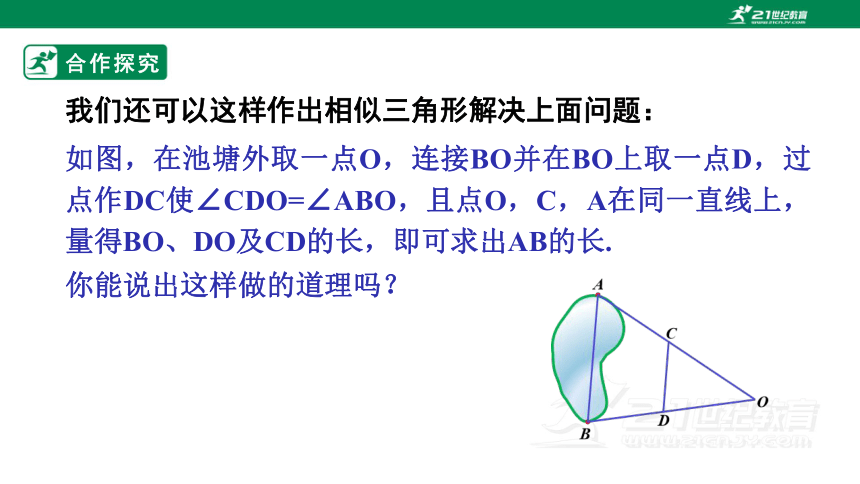
我们还可以这样作出相似三角形解决上面问题:
如图,在池塘外取一点O,连接BO并在BO上取一点D,过点作DC使∠CDO=∠ABO,且点O,C,A在同一直线上,量得BO、DO及CD的长,即可求出AB的长.
你能说出这样做的道理吗?
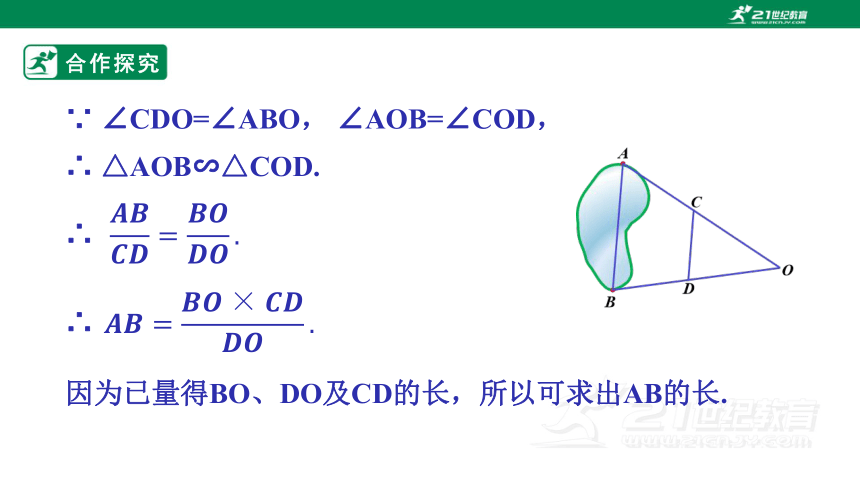
∵ ∠CDO=∠ABO, ∠AOB=∠COD,
合作探究
∴ △AOB∽△COD.
∴
∴
因为已量得BO、DO及CD的长,所以可求出AB的长.
例题教学
例 在用步枪瞄准靶心时,要使眼睛(O)、准星(A)、靶心点(B)在同一条直线上. 在射击时,李明由于有轻微抖动,致使准星A偏离到A′,如图3-34所示.已知OA=0.2cm,OB=50m,AA′=0.0005cm,求李明射击到的点B′偏离靶心点B的长度BB′(近似地认为AA′∥BB′).
例题教学
解 ∵ AA′∥BB′,
∵ OA=0.2cm,OB=50m, AA′=0.0005cm,
∴ △OAA′∥△OBB′,
∴
∴ BB′=0.125cm.
答:李明射击到的点B′偏离靶心点B的长度BB′为0.125cm.
方法小结
在实际生活中,当直接测量物体的高度比较困难时,可以在某一位置取一点,构造一对相似的直角三角形,利用测量工具取得一些线段的长,从而利用相似三角形的性质求得物体的高.
课堂练习
1. 如图,晓研同学测量旗杆AB的高度,在地面上竖一根2.4米长的竹竿DE,并在同一时刻下测得DE ,AB在地面上的影长EF=1.8米,BC=5.4米,则旗杆AB 长为( )
A. 6.4米
B. 7.2米
C. 8米
D. 9.6米
B
课堂练习
2. 如图是用手电筒测量房屋的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到房屋的顶端C处,已知AB=2米,且测得 BP=3 米,DP=12 米,那么该房屋的高度是 ( )
A. 6 米 B. 8 米
C. 18 米 D. 24 米
B
课堂练习
3. (安庆期末)如图,小明在A时测得某树的影长为1.5m,B时又测得某树的影长为6m.若两次日照的光线互相垂直,则树的高度为 .
思路:把树看作线段,由“两次日照的光线互相垂直”可知,A时和B时的影子所在直线与经过树梢的光线构成直角三角形.由于树所在线段垂直影子所在直线,因此图中的三角形相似.
课堂练习
解 如图,设两光线相交于点P,HM,HN分别为在A,B时的影长,则HM=1.5m,HN=6m.过点P作PH⊥MN.
∵ PH⊥MN,
∴ ∠PHM=∠PHN=90°.
又 PM⊥PN,即∠MPN=90°,
∴ ∠PMH+∠PNH=90°.
∴ ∠PMH+∠MPH=90°.
∴ ∠MPH=∠PNH.
课堂练习
∴ △PHM∽△PHN.
∴
即 PH =HM×HN=1.5×6=9.
∴ PH=3.
因此树的高为3m.
课堂总结
议一议:在实际问题中,相似三角形的应用有几种情况?解决问题的方法有哪些?
①求两点间的距离(或物体的宽).方法是构造相似三角形,利用相似三角形的性质解答;②求物体的高.方法是作垂线段,构造相似的直角三角形,利用相似三角形的性质解答。
板书设计
相似三角形的应用
求两点间的距离或物体的宽
求物体的高
思想:转化为相似三角形的问题
方法:构造相似三角形,作垂线
作业布置
第92、94页课练习第1、2题:
1. 如图,某路口栏杆的短臂长为1m,长臂长为6m.当短臂端点下降0.5米时,长臂端点升高多少米?
提示:证明三角形相似,利用“相似三角形对应高的比等于相似比”列式求解.
作业布置
2. 如图,小红同学用自制的直角三角形纸板DEF测量树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=80m,EF=40m,测得AC=1.5cm,CD=8m,求树高AB.
提示:先证明△DCB∽△DEF,利用相似三角形的性质求出BC,再加上人的高度AC即得树高AB.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.5 相似三角形的应用
湘教版九年级上册
教学目标
1. 能利用相似三角形测量、计算两点间的距离或线段长度.
2. 熟悉构造相似三角形的方法解决现实中的测量问题.
3. 提高分析问题、解决问题的能力.
4. 培养热爱生活的情感,激发学生学习数学的兴趣.
新知讲解
如图3-32,A,B两点分别位于一个池塘的两端,小张想量出A,B间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量方法吗?
新知讲解
我们可以这样做:
如图3-33,在池塘外取一点C,使它可以直接看到AB两点,连接并延长AC,BC,在AC的延长线上取一点D,在BC的
延长线上取一点E,使 (k为正整数),测量出DE的长度后,就可以由相似三角形的有关知识求出A,B两点间的距离了.
合作探究
如图3-33,如果2,且测得DE的长为50cm,则AB两点间的距离为多少?
做一做
合作探究
∵
∠ACB=∠DCE,
∴ △ABC∽△DEC.
∴
∵ DE=50,
∴ AB=2DE=100m.
方法小结
在实际生活中,当直接测量两点间的距离比较困难时,可以在容易测量线段长度的某一位置取一点,构造一对相似三角形,从而利用“相似三角形的对应边成比例”即可求得这两点间的距离,如一座小山两侧两个点之间的距离、一条河的宽度等.
合作探究
我们还可以这样作出相似三角形解决上面问题:
如图,在池塘外取一点O,连接BO并在BO上取一点D,过点作DC使∠CDO=∠ABO,且点O,C,A在同一直线上,量得BO、DO及CD的长,即可求出AB的长.
你能说出这样做的道理吗?
∵ ∠CDO=∠ABO, ∠AOB=∠COD,
合作探究
∴ △AOB∽△COD.
∴
∴
因为已量得BO、DO及CD的长,所以可求出AB的长.
例题教学
例 在用步枪瞄准靶心时,要使眼睛(O)、准星(A)、靶心点(B)在同一条直线上. 在射击时,李明由于有轻微抖动,致使准星A偏离到A′,如图3-34所示.已知OA=0.2cm,OB=50m,AA′=0.0005cm,求李明射击到的点B′偏离靶心点B的长度BB′(近似地认为AA′∥BB′).
例题教学
解 ∵ AA′∥BB′,
∵ OA=0.2cm,OB=50m, AA′=0.0005cm,
∴ △OAA′∥△OBB′,
∴
∴ BB′=0.125cm.
答:李明射击到的点B′偏离靶心点B的长度BB′为0.125cm.
方法小结
在实际生活中,当直接测量物体的高度比较困难时,可以在某一位置取一点,构造一对相似的直角三角形,利用测量工具取得一些线段的长,从而利用相似三角形的性质求得物体的高.
课堂练习
1. 如图,晓研同学测量旗杆AB的高度,在地面上竖一根2.4米长的竹竿DE,并在同一时刻下测得DE ,AB在地面上的影长EF=1.8米,BC=5.4米,则旗杆AB 长为( )
A. 6.4米
B. 7.2米
C. 8米
D. 9.6米
B
课堂练习
2. 如图是用手电筒测量房屋的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到房屋的顶端C处,已知AB=2米,且测得 BP=3 米,DP=12 米,那么该房屋的高度是 ( )
A. 6 米 B. 8 米
C. 18 米 D. 24 米
B
课堂练习
3. (安庆期末)如图,小明在A时测得某树的影长为1.5m,B时又测得某树的影长为6m.若两次日照的光线互相垂直,则树的高度为 .
思路:把树看作线段,由“两次日照的光线互相垂直”可知,A时和B时的影子所在直线与经过树梢的光线构成直角三角形.由于树所在线段垂直影子所在直线,因此图中的三角形相似.
课堂练习
解 如图,设两光线相交于点P,HM,HN分别为在A,B时的影长,则HM=1.5m,HN=6m.过点P作PH⊥MN.
∵ PH⊥MN,
∴ ∠PHM=∠PHN=90°.
又 PM⊥PN,即∠MPN=90°,
∴ ∠PMH+∠PNH=90°.
∴ ∠PMH+∠MPH=90°.
∴ ∠MPH=∠PNH.
课堂练习
∴ △PHM∽△PHN.
∴
即 PH =HM×HN=1.5×6=9.
∴ PH=3.
因此树的高为3m.
课堂总结
议一议:在实际问题中,相似三角形的应用有几种情况?解决问题的方法有哪些?
①求两点间的距离(或物体的宽).方法是构造相似三角形,利用相似三角形的性质解答;②求物体的高.方法是作垂线段,构造相似的直角三角形,利用相似三角形的性质解答。
板书设计
相似三角形的应用
求两点间的距离或物体的宽
求物体的高
思想:转化为相似三角形的问题
方法:构造相似三角形,作垂线
作业布置
第92、94页课练习第1、2题:
1. 如图,某路口栏杆的短臂长为1m,长臂长为6m.当短臂端点下降0.5米时,长臂端点升高多少米?
提示:证明三角形相似,利用“相似三角形对应高的比等于相似比”列式求解.
作业布置
2. 如图,小红同学用自制的直角三角形纸板DEF测量树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=80m,EF=40m,测得AC=1.5cm,CD=8m,求树高AB.
提示:先证明△DCB∽△DEF,利用相似三角形的性质求出BC,再加上人的高度AC即得树高AB.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
