高中数学必修第一册人教A版(2019)5.6 《函数y=Asin(ωx+φ)应用》名师 课件(共26张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)5.6 《函数y=Asin(ωx+φ)应用》名师 课件(共26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
复习引入
人教A版同步教材名师课件
函数 = ( + )应用
探究新知
y
x
o
2
-2
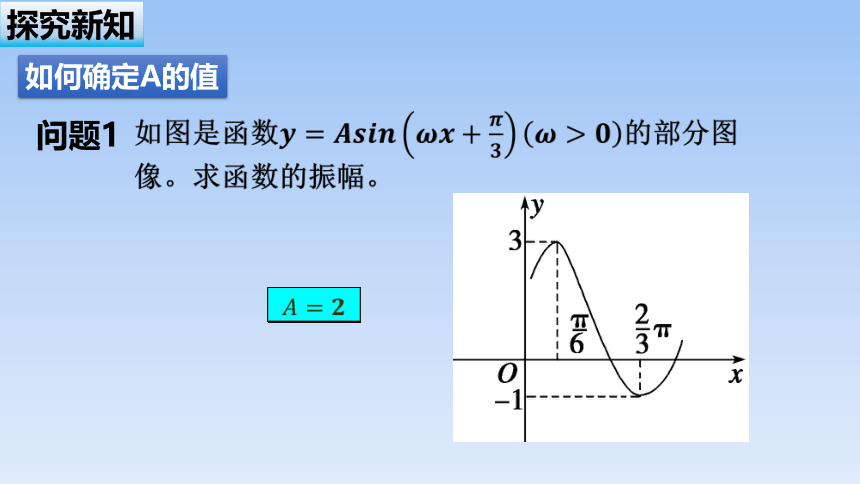
问题1
x
y
o
3
-3
探究新知
如何确定A的值
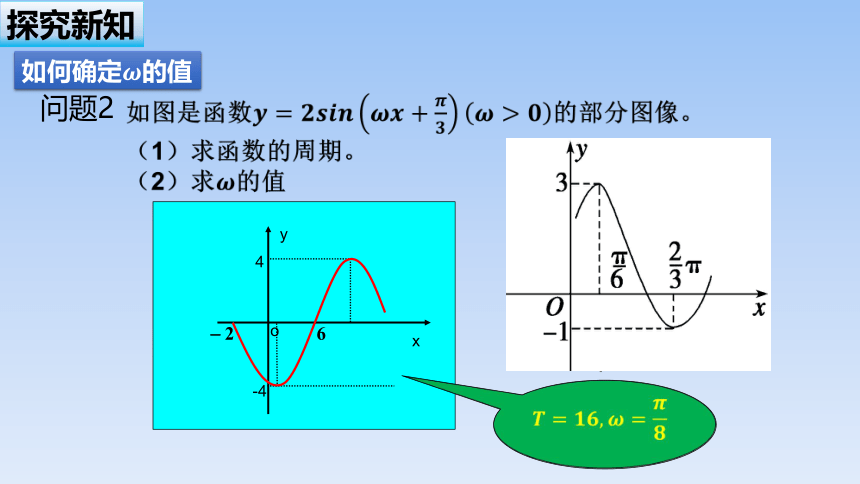
问题2
y
x
o
2
-2
y
x
o
2
-2
x
y
o
4
-4
探究新知
如何确定的值
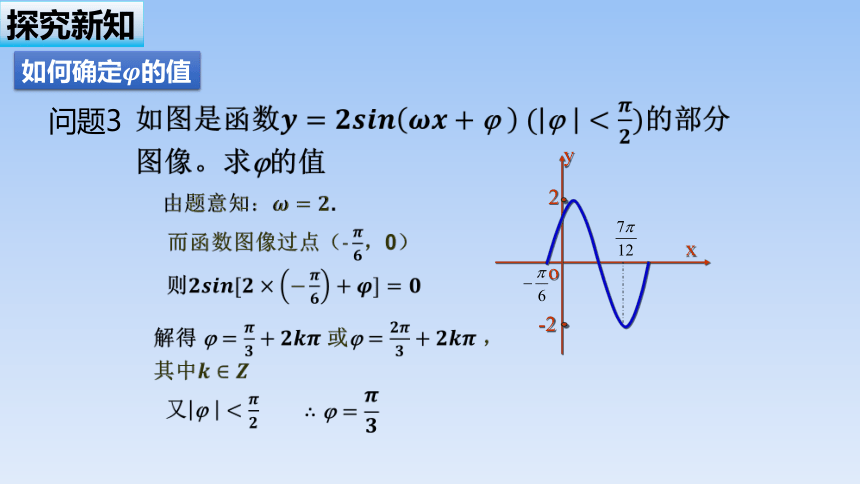
问题3
y
x
o
2
-2
探究新知
如何确定的值
① :一般可由图象上最大值、最小值来确定;
② :因 所以 一般通过求周期来确定 ,
相邻两个最高点(最低点)之间的距离为 ;
相邻的两条对称轴之间的距离为 ;
相邻的两个零点之间的距离为 ;
零点与相邻的对称轴之间的距离为 ;
③ :利用图象显示的五点中的一个点来确定 ;
也可用图象显示的五点中的两点列方程组解
若已知函数类型为可按以下规律来确定
探究新知
探究新知
典例讲解
例1、函数的部分图象如图所示,则解析式为 .
由图象知,周期,
所以,所以.
由,
所以,
所以.
解析
方法归纳
(1)直接从图象确定振幅和周期,则可确定函数式y=Asin(ωx+φ)中的参数A和ω,再选取最大值点的数据代入ωx+φ=2kπ+ ,k∈Z,结合φ的范围求出φ;
(2)通过若干特殊点代入函数式,通过解方程组求相关待定系数A,ω,φ.
(3)运用逆向思维的方法,先确定函数的基本函数式y=Asin ωx,再根据图象平移规律确定相关的参数.
根据函数的部分图象求解析式的方法
1.如图为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象的一部分,试求该函数的解析式.
变式训练
由图可得:A=,T=2|MN|=π.
从而ω= =2,故y= sin(2x+φ),
解析
将M代入得sin =0,
又|φ|<π,得φ=- ,
所以y= sin
函数的对称中心
典例讲解
例2、已知函数的最小正周期为,求的对称轴方程.
解析
由T= =π,解得ω=2,则f(x)= ,
令,得,
即对称轴方程为
令,得,
所以该函数的对称中心为
方法归纳
变式训练
2.把函数的图象向右平移φ个单位长度,所得到的图象正好关于y轴对称,则φ的最小正值是 .
解析
将y=的图象向右平移φ个单位长度,得y=的图象,
因为y=cos 的图象关于y轴对称,
所以cos =±1.所以φ =kπ,k∈Z.
当k=-1时,φ取得最小正值.
典例讲解
例3、已知函数y=Asin(ωx+φ) 的图象过点P,图象与P点最近的一个最高点坐标为.
(1)求函数的解析式;
(2)指出该函数的增区间;
(3)求使y≤0时,x的取值范围.
(1)因为图象的一个最高点坐标为,所以
所以.所以.
由于,所以.
又,所以,
所以.
解析
典例讲解
例3、已知函数y=Asin(ωx+φ) 的图象过点P,图象与P点最近的一个最高点坐标为.
(1)求函数的解析式;
(2)指出该函数的增区间;
(3)求使y≤0时,x的取值范围.
解析
(2)因为函数的增区间满足,所以
所以
所以增区间为.
典例讲解
例3、已知函数y=Asin(ωx+φ) 的图象过点P,图象与P点最近的一个最高点坐标为.
(1)求函数的解析式;
(2)指出该函数的增区间;
(3)求使y≤0时,x的取值范围.
解析
(3)因为,所以,
所以,
所以使y≤0时,x的取值范围是
方法归纳
(1)应用的范围:函数的单调性、最值、奇偶性、图象的对称性等方面都有体现和考查.
(2)解决的方法:有关函数y=Asin(ωx+φ)的性质的运用问题,充分利用三角函数的基本性质,要特别注意整体代换的思想的运用.
函数y=Asin(ωx+φ)性质的应用
变式训练
3.已知函数.
(1)求f(x)的振幅、最小正周期及单调增区间;
(2)求f(x)的图象的对称轴方程和对称中心;
(3)求f(x)的最小值及取得最小值时x的取值集合.
解析
(1)函数f(x)的振幅为,最小正周期T= =π,
由2kπ- ≤2x+ ≤2kπ+ (k∈Z),
得kπ- ≤x≤kπ+ (k∈Z),
所以f(x)的单调增区间为(k∈Z).
(2)令,得,
即对称轴方程为;
令,得,
所以该函数的对称中心为
变式训练
3.已知函数.
(1)求f(x)的振幅、最小正周期及单调增区间;
(2)求f(x)的图象的对称轴方程和对称中心;
(3)求f(x)的最小值及取得最小值时x的取值集合.
解析
(3) 即 ,
整理得, , 此时f(x)取得最小值为,
此时x的取值集合为
素养提炼
1.由函数y=Asin(ωx+φ)的部分图象确定解析式关键在于确定参数A,ω,φ的值.
(1)一般可由图象上的最大值、最小值来确定|A|.
(2)因为T= ,所以往往通过求周期T来确定ω,可通过已知曲线与x轴的交点从而确定T,即相邻的最高点与最低点所对应的横坐标之间的距离为;相邻的两个最高点(或最低点)之间的距离为T.
(3)求φ,常用方法有:
①代入法:把图象上的一个已知点代入转化求解.
②五点法:确定φ值时,往往以寻找“五点法”中的第一个零点作为突破口,具体如下:
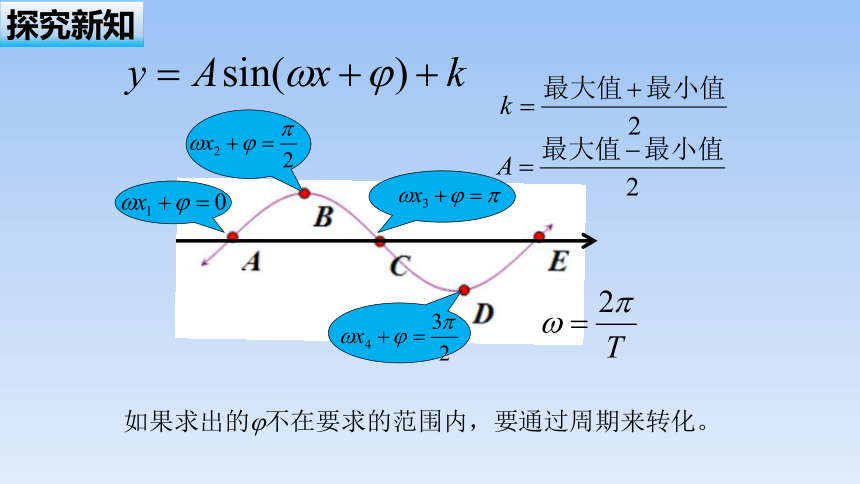
“第一点”(即图象上升时与x轴的交点)为ωx+φ=0;“第二点”(即图象的“峰点”)为ωx+φ= ;“第三点”(即图象下降时与x轴的交点)为ωx+φ=π;“第四点”(即图象的“谷点”)为ωx+φ=;“第五点”为ωx+φ=2π.
当堂练习
1.已知函数的最小正周期为,则该函数的图象( )
A.关于点对称 B.关于直线对称
C.关于点对称 D.关于直线对称
2.同时具有性质“(1)最小正周期是;(2)图象关于直线对称;(3)在上单调递增”的一个函数是( )
A
C
3.已知函数的部分图象如图所示,则等于( )
B
A. B.0 C.2 D.-2
当堂练习
4.已知是实数,则函数的图象不可能是( )
D
5.函数的部分图象如图所示,则,的值分别是( )
A
当堂练习
6.函数(其中)的部分图象如图所示,为了得到函数的图象,则只需将的图象( )
D
A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
归纳小结
函数 的性质
定义域、值域
周期性
单调性
奇偶性
对称性
应用
求解析式
1.
2.在研究 的性质时,注意采用整体代换的思想.例如,它在 =时取得最大值,在 = 时取得最小值.
P241:4、5、7
作 业
复习引入
人教A版同步教材名师课件
函数 = ( + )应用
探究新知
y
x
o
2
-2
问题1
x
y
o
3
-3
探究新知
如何确定A的值
问题2
y
x
o
2
-2
y
x
o
2
-2
x
y
o
4
-4
探究新知
如何确定的值
问题3
y
x
o
2
-2
探究新知
如何确定的值
① :一般可由图象上最大值、最小值来确定;
② :因 所以 一般通过求周期来确定 ,
相邻两个最高点(最低点)之间的距离为 ;
相邻的两条对称轴之间的距离为 ;
相邻的两个零点之间的距离为 ;
零点与相邻的对称轴之间的距离为 ;
③ :利用图象显示的五点中的一个点来确定 ;
也可用图象显示的五点中的两点列方程组解
若已知函数类型为可按以下规律来确定
探究新知
探究新知
典例讲解
例1、函数的部分图象如图所示,则解析式为 .
由图象知,周期,
所以,所以.
由,
所以,
所以.
解析
方法归纳
(1)直接从图象确定振幅和周期,则可确定函数式y=Asin(ωx+φ)中的参数A和ω,再选取最大值点的数据代入ωx+φ=2kπ+ ,k∈Z,结合φ的范围求出φ;
(2)通过若干特殊点代入函数式,通过解方程组求相关待定系数A,ω,φ.
(3)运用逆向思维的方法,先确定函数的基本函数式y=Asin ωx,再根据图象平移规律确定相关的参数.
根据函数的部分图象求解析式的方法
1.如图为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象的一部分,试求该函数的解析式.
变式训练
由图可得:A=,T=2|MN|=π.
从而ω= =2,故y= sin(2x+φ),
解析
将M代入得sin =0,
又|φ|<π,得φ=- ,
所以y= sin
函数的对称中心
典例讲解
例2、已知函数的最小正周期为,求的对称轴方程.
解析
由T= =π,解得ω=2,则f(x)= ,
令,得,
即对称轴方程为
令,得,
所以该函数的对称中心为
方法归纳
变式训练
2.把函数的图象向右平移φ个单位长度,所得到的图象正好关于y轴对称,则φ的最小正值是 .
解析
将y=的图象向右平移φ个单位长度,得y=的图象,
因为y=cos 的图象关于y轴对称,
所以cos =±1.所以φ =kπ,k∈Z.
当k=-1时,φ取得最小正值.
典例讲解
例3、已知函数y=Asin(ωx+φ) 的图象过点P,图象与P点最近的一个最高点坐标为.
(1)求函数的解析式;
(2)指出该函数的增区间;
(3)求使y≤0时,x的取值范围.
(1)因为图象的一个最高点坐标为,所以
所以.所以.
由于,所以.
又,所以,
所以.
解析
典例讲解
例3、已知函数y=Asin(ωx+φ) 的图象过点P,图象与P点最近的一个最高点坐标为.
(1)求函数的解析式;
(2)指出该函数的增区间;
(3)求使y≤0时,x的取值范围.
解析
(2)因为函数的增区间满足,所以
所以
所以增区间为.
典例讲解
例3、已知函数y=Asin(ωx+φ) 的图象过点P,图象与P点最近的一个最高点坐标为.
(1)求函数的解析式;
(2)指出该函数的增区间;
(3)求使y≤0时,x的取值范围.
解析
(3)因为,所以,
所以,
所以使y≤0时,x的取值范围是
方法归纳
(1)应用的范围:函数的单调性、最值、奇偶性、图象的对称性等方面都有体现和考查.
(2)解决的方法:有关函数y=Asin(ωx+φ)的性质的运用问题,充分利用三角函数的基本性质,要特别注意整体代换的思想的运用.
函数y=Asin(ωx+φ)性质的应用
变式训练
3.已知函数.
(1)求f(x)的振幅、最小正周期及单调增区间;
(2)求f(x)的图象的对称轴方程和对称中心;
(3)求f(x)的最小值及取得最小值时x的取值集合.
解析
(1)函数f(x)的振幅为,最小正周期T= =π,
由2kπ- ≤2x+ ≤2kπ+ (k∈Z),
得kπ- ≤x≤kπ+ (k∈Z),
所以f(x)的单调增区间为(k∈Z).
(2)令,得,
即对称轴方程为;
令,得,
所以该函数的对称中心为
变式训练
3.已知函数.
(1)求f(x)的振幅、最小正周期及单调增区间;
(2)求f(x)的图象的对称轴方程和对称中心;
(3)求f(x)的最小值及取得最小值时x的取值集合.
解析
(3) 即 ,
整理得, , 此时f(x)取得最小值为,
此时x的取值集合为
素养提炼
1.由函数y=Asin(ωx+φ)的部分图象确定解析式关键在于确定参数A,ω,φ的值.
(1)一般可由图象上的最大值、最小值来确定|A|.
(2)因为T= ,所以往往通过求周期T来确定ω,可通过已知曲线与x轴的交点从而确定T,即相邻的最高点与最低点所对应的横坐标之间的距离为;相邻的两个最高点(或最低点)之间的距离为T.
(3)求φ,常用方法有:
①代入法:把图象上的一个已知点代入转化求解.
②五点法:确定φ值时,往往以寻找“五点法”中的第一个零点作为突破口,具体如下:
“第一点”(即图象上升时与x轴的交点)为ωx+φ=0;“第二点”(即图象的“峰点”)为ωx+φ= ;“第三点”(即图象下降时与x轴的交点)为ωx+φ=π;“第四点”(即图象的“谷点”)为ωx+φ=;“第五点”为ωx+φ=2π.
当堂练习
1.已知函数的最小正周期为,则该函数的图象( )
A.关于点对称 B.关于直线对称
C.关于点对称 D.关于直线对称
2.同时具有性质“(1)最小正周期是;(2)图象关于直线对称;(3)在上单调递增”的一个函数是( )
A
C
3.已知函数的部分图象如图所示,则等于( )
B
A. B.0 C.2 D.-2
当堂练习
4.已知是实数,则函数的图象不可能是( )
D
5.函数的部分图象如图所示,则,的值分别是( )
A
当堂练习
6.函数(其中)的部分图象如图所示,为了得到函数的图象,则只需将的图象( )
D
A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
归纳小结
函数 的性质
定义域、值域
周期性
单调性
奇偶性
对称性
应用
求解析式
1.
2.在研究 的性质时,注意采用整体代换的思想.例如,它在 =时取得最大值,在 = 时取得最小值.
P241:4、5、7
作 业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
