高中数学必修第一册人教A版(2019)5.6.2《φ,ω,A对函数y=Asin(ωx+φ)图象的影响》教学设计一(表格式)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)5.6.2《φ,ω,A对函数y=Asin(ωx+φ)图象的影响》教学设计一(表格式) | 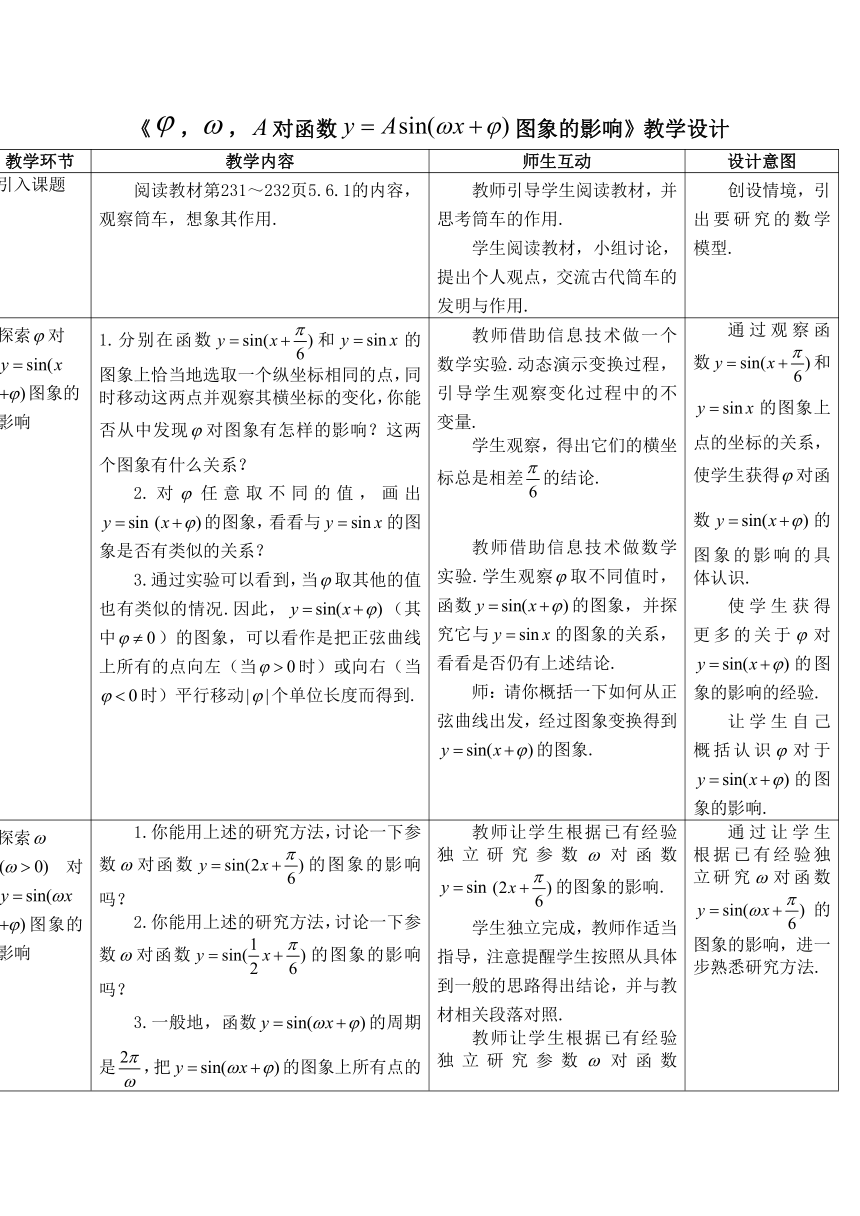 | |
| 格式 | docx | ||
| 文件大小 | 292.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 17:35:07 | ||
图片预览


文档简介
《,,对函数图象的影响》教学设计
教学环节 教学内容 师生互动 设计意图
引入课题 阅读教材第231~232页5.6.1的内容,观察筒车,想象其作用. 教师引导学生阅读教材,并思考筒车的作用. 学生阅读教材,小组讨论,提出个人观点,交流古代筒车的发明与作用. 创设情境,引出要研究的数学模型.
探索对图象的影响 1.分别在函数和的图象上恰当地选取一个纵坐标相同的点,同时移动这两点并观察其横坐标的变化,你能否从中发现对图象有怎样的影响?这两个图象有什么关系? 2.对任意取不同的值,画出的图象,看看与的图象是否有类似的关系? 3.通过实验可以看到,当取其他的值也有类似的情况.因此,(其中)的图象,可以看作是把正弦曲线上所有的点向左(当时)或向右(当时)平行移动个单位长度而得到. 教师借助信息技术做一个数学实验.动态演示变换过程,引导学生观察变化过程中的不变量. 学生观察,得出它们的横坐标总是相差的结论. 教师借助信息技术做数学实验.学生观察取不同值时,函数的图象,并探究它与的图象的关系,看看是否仍有上述结论. 师:请你概括一下如何从正弦曲线出发,经过图象变换得到的图象. 通过观察函数和的图象上点的坐标的关系,使学生获得对函数的图象的影响的具体认识. 使学生获得更多的关于对的图象的影响的经验. 让学生自己概括认识对于的图象的影响.
探索 对图象的影响 1.你能用上述的研究方法,讨论一下参数对函数的图象的影响吗? 2.你能用上述的研究方法,讨论一下参数对函数的图象的影响吗? 3.一般地,函数的周期是,把的图象上所有点的横坐标缩短(当时)或伸长(当时)到原来的倍(纵坐标不变),就得到的图象. 教师让学生根据已有经验独立研究参数对函数的图象的影响. 学生独立完成,教师作适当指导,注意提醒学生按照从具体到一般的思路得出结论,并与教材相关段落对照. 教师让学生根据已有经验独立研究参数对函数的图象的影响. 学生独立完成,教师作适当指导,注意提醒学生按照从具体到一般的思路得出结论,并与教材相关段落对照. 教师引导学生总结参数对函数的图象的影响. 学生小组合作探索总结.学生展示,教师补充完善,得出结论. 通过让学生根据已有经验独立研究对函数的图象的影响,进一步熟悉研究方法.
探索 对图象的影响 1.你能讨论一下参数对的图象的影响吗? 2.你能讨论一下参数对的图象的影响吗? 3.一般地,函数的图象,可以看作是把图象上所有点的纵坐标伸长(当时)或缩短(当时)到原来的倍(横坐标不变)而得到.从而,函数的值域是,最大值是,最小值是. 教师指派一名学生借助信息技术画出时,函数的图象,并观察与的图象之间的关系. 学生画图,并观察变化规律. 引导学生总结,并与教材相关段落对照. 教师让学生借助信息技术画出时,函数的图象,并观察与的图象之间的关系. 学生画图,并观察变化规律. 教师引导学生总结参数对函数的图象的影响. 学生小组合作探索总结.学生展示,教师补充完善,得出结论. 巩固已有经验,认识参数对的图象的影响. 提升学生的总结归纳能力.
探索与,的图象之间的变换关系 由的图象得到的图象的变换,参数的变换顺序为. (1)请同学们思考:还有几种其他的变换方法吗? (2)若参数的变换顺序为,则图象变换的规律是怎样的? 若参数的变换顺序为,则图象变换规律如下: 把的图象上各点的横坐标都变为原来的倍,可得的图象;把所得曲线向左(向右)平移个单位长度,可得的图象;再把曲线上各点的纵坐标变为原来的倍,得到的图象. 教师提出问题(1),学生回答后给出评价. 学生思考问题(1),讨论、交流、回答. 教师让学生思考问题(2),先探究按下列顺序进行图象变换的规律.让学生回答探究结果.共同归纳变换顺序为 的图象的变换规律. 师生归纳总结: 由函数的图象得到的图象的两种途径可以通过图形表示,如下图. 使学生掌握由的图象得到的图象的变换方法.提升逻辑推理核心素养.
应用举例 例 画出函数的简图. 例题变式 画出函数的简图. 练习:教材第239页练习第2题. 教师提出问题: (1)函数的图象和的图象关系如何? (2)函数的图象和的图象关系如何? (3)函数的图象和的图象关系如何? 学生小组讨论,派代表回答. 师:如果将例题中的“3”换成“4”呢?情况如何? 学生独立完成练习. 引导学生积极参与对例题的学习,调动学生的积极性. 检查学生的掌握情况.
课堂小结 1.我们如何得到函数的图象?(利用图象变换) 2.利用图象变换法如何由函数的图象得到函数的图象? 教师提出问题,学生讨论. 学生小组合作总结,选出代表表述. 引导学生主动学习,调动学生的积极性.
布置作业 1.教材第239页练习第1题. 2.选做题 教材第240页习题5.6第1题. 学生独立完成作业,教师批阅. 通过分层作业使学生巩固所学内容,并为有余力的学生提供进一步学习的机会.
板书设计
第1课时 ,,对函数图象的影响 一、课题引入 二、新课探究 1.探索对图象的影响 2.探索对图象的影响 3.探索对图象的影响 4.探索与,的图象之间的变换关系 三、应用举例 例 画出函数的简图. 例题变式 画出函数的简图 练习 四、课堂小结 五、布置作业
教学环节 教学内容 师生互动 设计意图
引入课题 阅读教材第231~232页5.6.1的内容,观察筒车,想象其作用. 教师引导学生阅读教材,并思考筒车的作用. 学生阅读教材,小组讨论,提出个人观点,交流古代筒车的发明与作用. 创设情境,引出要研究的数学模型.
探索对图象的影响 1.分别在函数和的图象上恰当地选取一个纵坐标相同的点,同时移动这两点并观察其横坐标的变化,你能否从中发现对图象有怎样的影响?这两个图象有什么关系? 2.对任意取不同的值,画出的图象,看看与的图象是否有类似的关系? 3.通过实验可以看到,当取其他的值也有类似的情况.因此,(其中)的图象,可以看作是把正弦曲线上所有的点向左(当时)或向右(当时)平行移动个单位长度而得到. 教师借助信息技术做一个数学实验.动态演示变换过程,引导学生观察变化过程中的不变量. 学生观察,得出它们的横坐标总是相差的结论. 教师借助信息技术做数学实验.学生观察取不同值时,函数的图象,并探究它与的图象的关系,看看是否仍有上述结论. 师:请你概括一下如何从正弦曲线出发,经过图象变换得到的图象. 通过观察函数和的图象上点的坐标的关系,使学生获得对函数的图象的影响的具体认识. 使学生获得更多的关于对的图象的影响的经验. 让学生自己概括认识对于的图象的影响.
探索 对图象的影响 1.你能用上述的研究方法,讨论一下参数对函数的图象的影响吗? 2.你能用上述的研究方法,讨论一下参数对函数的图象的影响吗? 3.一般地,函数的周期是,把的图象上所有点的横坐标缩短(当时)或伸长(当时)到原来的倍(纵坐标不变),就得到的图象. 教师让学生根据已有经验独立研究参数对函数的图象的影响. 学生独立完成,教师作适当指导,注意提醒学生按照从具体到一般的思路得出结论,并与教材相关段落对照. 教师让学生根据已有经验独立研究参数对函数的图象的影响. 学生独立完成,教师作适当指导,注意提醒学生按照从具体到一般的思路得出结论,并与教材相关段落对照. 教师引导学生总结参数对函数的图象的影响. 学生小组合作探索总结.学生展示,教师补充完善,得出结论. 通过让学生根据已有经验独立研究对函数的图象的影响,进一步熟悉研究方法.
探索 对图象的影响 1.你能讨论一下参数对的图象的影响吗? 2.你能讨论一下参数对的图象的影响吗? 3.一般地,函数的图象,可以看作是把图象上所有点的纵坐标伸长(当时)或缩短(当时)到原来的倍(横坐标不变)而得到.从而,函数的值域是,最大值是,最小值是. 教师指派一名学生借助信息技术画出时,函数的图象,并观察与的图象之间的关系. 学生画图,并观察变化规律. 引导学生总结,并与教材相关段落对照. 教师让学生借助信息技术画出时,函数的图象,并观察与的图象之间的关系. 学生画图,并观察变化规律. 教师引导学生总结参数对函数的图象的影响. 学生小组合作探索总结.学生展示,教师补充完善,得出结论. 巩固已有经验,认识参数对的图象的影响. 提升学生的总结归纳能力.
探索与,的图象之间的变换关系 由的图象得到的图象的变换,参数的变换顺序为. (1)请同学们思考:还有几种其他的变换方法吗? (2)若参数的变换顺序为,则图象变换的规律是怎样的? 若参数的变换顺序为,则图象变换规律如下: 把的图象上各点的横坐标都变为原来的倍,可得的图象;把所得曲线向左(向右)平移个单位长度,可得的图象;再把曲线上各点的纵坐标变为原来的倍,得到的图象. 教师提出问题(1),学生回答后给出评价. 学生思考问题(1),讨论、交流、回答. 教师让学生思考问题(2),先探究按下列顺序进行图象变换的规律.让学生回答探究结果.共同归纳变换顺序为 的图象的变换规律. 师生归纳总结: 由函数的图象得到的图象的两种途径可以通过图形表示,如下图. 使学生掌握由的图象得到的图象的变换方法.提升逻辑推理核心素养.
应用举例 例 画出函数的简图. 例题变式 画出函数的简图. 练习:教材第239页练习第2题. 教师提出问题: (1)函数的图象和的图象关系如何? (2)函数的图象和的图象关系如何? (3)函数的图象和的图象关系如何? 学生小组讨论,派代表回答. 师:如果将例题中的“3”换成“4”呢?情况如何? 学生独立完成练习. 引导学生积极参与对例题的学习,调动学生的积极性. 检查学生的掌握情况.
课堂小结 1.我们如何得到函数的图象?(利用图象变换) 2.利用图象变换法如何由函数的图象得到函数的图象? 教师提出问题,学生讨论. 学生小组合作总结,选出代表表述. 引导学生主动学习,调动学生的积极性.
布置作业 1.教材第239页练习第1题. 2.选做题 教材第240页习题5.6第1题. 学生独立完成作业,教师批阅. 通过分层作业使学生巩固所学内容,并为有余力的学生提供进一步学习的机会.
板书设计
第1课时 ,,对函数图象的影响 一、课题引入 二、新课探究 1.探索对图象的影响 2.探索对图象的影响 3.探索对图象的影响 4.探索与,的图象之间的变换关系 三、应用举例 例 画出函数的简图. 例题变式 画出函数的简图 练习 四、课堂小结 五、布置作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
