高中数学必修第一册人教A版(2019)《三角函数的应用---习题课》名师课件(共28张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)《三角函数的应用---习题课》名师课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-13 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
人教A版同步教材名师课件
三角函数的应用
---习题课
典例讲解
例1、如图,某地一天 6~16 时的温度变化曲线近似满足函数
( 1 ) 求这一天 6 16 时的最大温差;
( 2 ) 根据图象确定这段曲线的函数解析式,并估计 16 时的气温.
( 结果精确到 0.1 ℃.参考数据: )
典例讲解
(1)最大温差为
(2)依题意,
由
且解得
这段曲线的函数解析式为
即 16 时的气温大概是
解析
方法归纳
已知函数模型解决实际问题的思路
这类题一般明确地指出了周期现象满足的变化规律,例如,周期现象可用形如或的函数来刻画, 解这样的题一般很容易, 只需根据已知条件确定参数, 求出函数解析式,再将题目涉及的具体的值代入计算即可.
三角函数模型中函数解析式的应用主要是对相关量物理意义的考查.
变式训练
1.如图, 某地某天从 8~14 时用电量变化曲线近似满足函数
(1) 指出这一时间段的最大用电量及最小用电量;
(2) 求出 的值,写出这段曲线的函数解析式.
解析
最大用电量为 50 万千瓦时,最小用电量为 30 万千瓦时.
变式训练
解析
(2) 观察图象可知, 8~14 时的图象是的半个周期的图像
将代入上式,结合解得
所求解析式为
典例讲解
例2、如图是电流强度(单位:安) 随时间 (单位:秒) 变化的函数
的图像,的秒时,电流强度是________安
由图象可知,A=10,周期
所以,所以
当秒时, (安)
解析
5
方法归纳
(1)在物理学科中,很多是以三角函数为模型的问题,如简谐运动等,通过建立三角函数模型求解相应的问题.
(2)由于物理学中的单摆、光波、机械波、交流电流等都具有周期性,且与三角函数的相关知识相吻合, 因此常借助于三角函数模型来研究物理学中的相关知识.
(3)在物理学中,物体做简谐运动时可用正弦型函数表示物体运动的位移 随时间 的变化规律.
变式训练
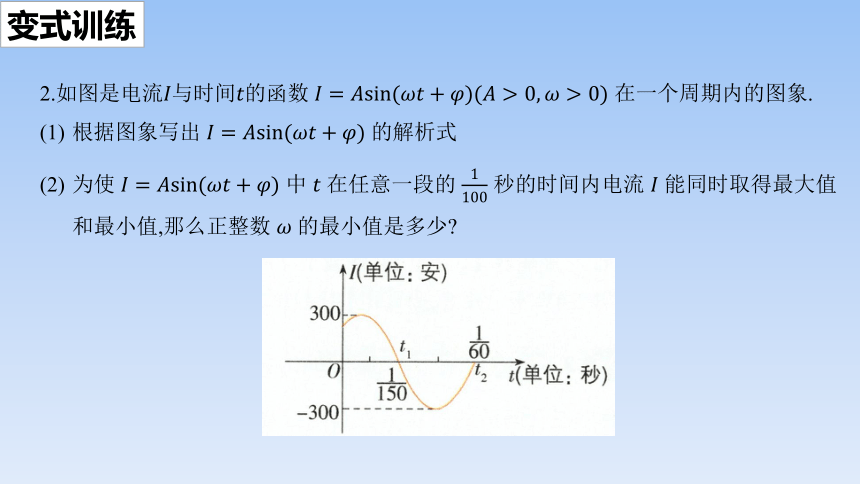
2.如图是电流与时间的函数 在一个周期内的图象.
根据图象写出 的解析式
为使 中 在任意一段的 秒的时间内电流 能同时取得最大值和最小值,那么正整数 的最小值是多少
变式训练
解析
由题图知
由 知
(2) 问题等价于 即也即
故正整数 的最小值为
典例讲解
例3、如图,某动物种群数量在 1 月 1 日低至 700,7 月 1 日高至 900,其总量在两值之间依正弦型曲线变化
(1)求出种群数量 y 关于时间 t 的函数表达式;(其中 t 以年初以来的月为计量单位)
(2)估计当年 3 月 1 日动物种群数量.
典例讲解
(1) 设种群数量 关于 的函数解析式为
解得
又周期
又当
(2) 当时即当年 3 月 1 日动物种群数量约是 750.
解析
方法归纳
利用三角函数有关知识建立三角函数模型的基本思路
当实际问题具有几何背景, 而且动点的变化以及变量被某个角制约时, 不妨设此角为变量角,把所要求解的目标变量用此变量角的三角函数表示出来,建立三角函数模型解决相关问题.
变式训练
3.已知某帆船中心比赛场馆区的海面上每天海浪高度 (单位:米)可看作是时间 的函数,记作 ,经过长期观测 的曲线可近似地看成是函数 的图象, 下表是某日各时的浪高数据, 则最能近似地表示表中数据间对应关系的函数是 ( )
A. B.
C. D.
0 3 6 9 12 15 18 21 24
2 1 2 0.99 2
B
典例讲解
例4、如图,某市拟在长为 8 km 的道路 的一侧修建一条运动赛道,赛道的前一部分为曲线 该曲线段为函数的图象,且图象的最高点为;赛道的后一部分为折线段 为保证参赛运动员的安全,限定 求 的值和 两点间的距离.
典例讲解
依题意,有 又
当 时
又
解析
思路解析
由图得到 及函数的周期,利用三角函数的周期公式求得 将 的横坐标代入求出 的纵坐标,再利用两点间距离公式, 即可求解 两点间的距离.
变式训练
4.如图, 某污水处理厂要在一个矩形污水处理池的池底水平铺设污水净化管道 (是直角顶点) 来处理污水,管道越长,污水净化效果越好.设计要求管道的接口是的中点,,分别落在线段,上.已知米, 米,记
(1) 试将污水净化管道的总长度 ( 即 的周长,单位: 米) 表示为 的函数,并求出定义域;
(2) 问当 取何值时,污水净化效果最好?
并求出此时管道的总长度
变式训练
解析
(1)
由于
所以故
管道的总长度定义域为
变式训练
解析
(2).
设则,
由于,所以,
因为在内单调递减,
于是当时取得最大值米(此时或)
故当或时,污水净化效果最好,此时管道的总长度为米
典例讲解
例5、如图所示为一个观览车示意图,该观览车半径为4.8 m,圆上最低点与地面距离为 0.8m,60秒转动一圈,图中 与地面垂直,以 为始边,逆时针转动 角到 设 点与地面距离为 m.
求 与 之间关系的函数解析式;
设从 开始转动,经过 秒到达 求 与 间的函数解析式.
典例讲解
当 时
当 或 时,上述解析式也适合.
综上所述
(2) 点 在 上逆时针运动的角速度是
秒转过的角的弧度数为
解析
(1)过点 作地面的平行线 过点 作 的垂线 交 于 点.
变式训练
5.如图所示, 某幼儿园有一个矩形游乐场其中米,,由于幼儿园招生规模增大,需将该游乐场扩大成矩形区域, 要求 四个点分别在矩形 的四条边(不含顶点) 上.设(弧度), 的长为米
(1) 求 关于 的函数表达式;
(2) 求矩形区域 的面积 的最大值.
变式训练
解析
(1)由,得,又
所以由,得,即
(2)由(1)知
所以
当 时 取得最大值,且最大值为4050平方米
典例讲解
例6、 某山顶每隔 2 小时测得的温度( ℃ ) 如下表:
(1) 以时刻 (单位:时 )为横坐标,气温 (单位:℃) 为纵坐标,画出散点图;
(2) 用正弦型曲线去拟合这些数据,写出 关于 的函数解析式.
时刻 0 2 4 6 8 10 12 14 16 18 20 22 24
气温 13.5 6 1 -2 1.4 5.9 14.1 22.5 27.5 28 27.3 21 14.5
思路解析
先画出散点图,再根据散点图探求 与 的函数关系式
典例讲解
(2)设气温 关于 的解析式为
则 解得 又周期
又当 时,
解析
散点图如图所示.
方法归纳
(1)拟合模型的组建
⒈拟合模型是通过对有关变量的观测, 对数据的观察、分析及选择恰当的数学表达方式而得到的. 它的实质是数据拟合的精度和表达式简化程度的折中,折中方案的选择取决于实际需要.
(2)拟合的主要方法
⒈经验拟合: 选择规律简单的数学表达式, 讨论变量间的内在规律, 允许存在一定的误差;
⒉插值拟合:要求精确拟合相关数据, 即在观测点之间插入适当的数值.
(3)拟合的步骤
⒈根据原始数据、表格绘出散点图
⒉通过散点图,画出“最贴近”的直线或曲线,即拟合直线或拟合曲线;
⒊根据所学的函数知识,求出拟合直线或拟合曲线的函数解析式;
⒋利用函数解析式,根据条件对所给问题进行预测和控制,以便为决策和管理提供依据.
变式训练
6.一般地,人的体温是时刻变化的. 下表中给出了在 24 h 期间某人的体温的典型变化 (从夜间零点开始计时)
(1) 作出这些数据的散点图
(2) 选用一个三角函数来近似描述这些数据
时间/h 温度/ ℃
0 36.8
2 36.7
4 36.6
6 36.7
8 36.8
10 37
12 37.2
时间/h 温度/℃
14 37.3
16 37.4
18 37.3
20 37.2
22 37
24 36.8
变式训练
解析
(2) 设 ,
则
由
得取
故可用函数来近似描述这些数据.
(1)设时间为 温度为 散点图如图 :
人教A版同步教材名师课件
三角函数的应用
---习题课
典例讲解
例1、如图,某地一天 6~16 时的温度变化曲线近似满足函数
( 1 ) 求这一天 6 16 时的最大温差;
( 2 ) 根据图象确定这段曲线的函数解析式,并估计 16 时的气温.
( 结果精确到 0.1 ℃.参考数据: )
典例讲解
(1)最大温差为
(2)依题意,
由
且解得
这段曲线的函数解析式为
即 16 时的气温大概是
解析
方法归纳
已知函数模型解决实际问题的思路
这类题一般明确地指出了周期现象满足的变化规律,例如,周期现象可用形如或的函数来刻画, 解这样的题一般很容易, 只需根据已知条件确定参数, 求出函数解析式,再将题目涉及的具体的值代入计算即可.
三角函数模型中函数解析式的应用主要是对相关量物理意义的考查.
变式训练
1.如图, 某地某天从 8~14 时用电量变化曲线近似满足函数
(1) 指出这一时间段的最大用电量及最小用电量;
(2) 求出 的值,写出这段曲线的函数解析式.
解析
最大用电量为 50 万千瓦时,最小用电量为 30 万千瓦时.
变式训练
解析
(2) 观察图象可知, 8~14 时的图象是的半个周期的图像
将代入上式,结合解得
所求解析式为
典例讲解
例2、如图是电流强度(单位:安) 随时间 (单位:秒) 变化的函数
的图像,的秒时,电流强度是________安
由图象可知,A=10,周期
所以,所以
当秒时, (安)
解析
5
方法归纳
(1)在物理学科中,很多是以三角函数为模型的问题,如简谐运动等,通过建立三角函数模型求解相应的问题.
(2)由于物理学中的单摆、光波、机械波、交流电流等都具有周期性,且与三角函数的相关知识相吻合, 因此常借助于三角函数模型来研究物理学中的相关知识.
(3)在物理学中,物体做简谐运动时可用正弦型函数表示物体运动的位移 随时间 的变化规律.
变式训练
2.如图是电流与时间的函数 在一个周期内的图象.
根据图象写出 的解析式
为使 中 在任意一段的 秒的时间内电流 能同时取得最大值和最小值,那么正整数 的最小值是多少
变式训练
解析
由题图知
由 知
(2) 问题等价于 即也即
故正整数 的最小值为
典例讲解
例3、如图,某动物种群数量在 1 月 1 日低至 700,7 月 1 日高至 900,其总量在两值之间依正弦型曲线变化
(1)求出种群数量 y 关于时间 t 的函数表达式;(其中 t 以年初以来的月为计量单位)
(2)估计当年 3 月 1 日动物种群数量.
典例讲解
(1) 设种群数量 关于 的函数解析式为
解得
又周期
又当
(2) 当时即当年 3 月 1 日动物种群数量约是 750.
解析
方法归纳
利用三角函数有关知识建立三角函数模型的基本思路
当实际问题具有几何背景, 而且动点的变化以及变量被某个角制约时, 不妨设此角为变量角,把所要求解的目标变量用此变量角的三角函数表示出来,建立三角函数模型解决相关问题.
变式训练
3.已知某帆船中心比赛场馆区的海面上每天海浪高度 (单位:米)可看作是时间 的函数,记作 ,经过长期观测 的曲线可近似地看成是函数 的图象, 下表是某日各时的浪高数据, 则最能近似地表示表中数据间对应关系的函数是 ( )
A. B.
C. D.
0 3 6 9 12 15 18 21 24
2 1 2 0.99 2
B
典例讲解
例4、如图,某市拟在长为 8 km 的道路 的一侧修建一条运动赛道,赛道的前一部分为曲线 该曲线段为函数的图象,且图象的最高点为;赛道的后一部分为折线段 为保证参赛运动员的安全,限定 求 的值和 两点间的距离.
典例讲解
依题意,有 又
当 时
又
解析
思路解析
由图得到 及函数的周期,利用三角函数的周期公式求得 将 的横坐标代入求出 的纵坐标,再利用两点间距离公式, 即可求解 两点间的距离.
变式训练
4.如图, 某污水处理厂要在一个矩形污水处理池的池底水平铺设污水净化管道 (是直角顶点) 来处理污水,管道越长,污水净化效果越好.设计要求管道的接口是的中点,,分别落在线段,上.已知米, 米,记
(1) 试将污水净化管道的总长度 ( 即 的周长,单位: 米) 表示为 的函数,并求出定义域;
(2) 问当 取何值时,污水净化效果最好?
并求出此时管道的总长度
变式训练
解析
(1)
由于
所以故
管道的总长度定义域为
变式训练
解析
(2).
设则,
由于,所以,
因为在内单调递减,
于是当时取得最大值米(此时或)
故当或时,污水净化效果最好,此时管道的总长度为米
典例讲解
例5、如图所示为一个观览车示意图,该观览车半径为4.8 m,圆上最低点与地面距离为 0.8m,60秒转动一圈,图中 与地面垂直,以 为始边,逆时针转动 角到 设 点与地面距离为 m.
求 与 之间关系的函数解析式;
设从 开始转动,经过 秒到达 求 与 间的函数解析式.
典例讲解
当 时
当 或 时,上述解析式也适合.
综上所述
(2) 点 在 上逆时针运动的角速度是
秒转过的角的弧度数为
解析
(1)过点 作地面的平行线 过点 作 的垂线 交 于 点.
变式训练
5.如图所示, 某幼儿园有一个矩形游乐场其中米,,由于幼儿园招生规模增大,需将该游乐场扩大成矩形区域, 要求 四个点分别在矩形 的四条边(不含顶点) 上.设(弧度), 的长为米
(1) 求 关于 的函数表达式;
(2) 求矩形区域 的面积 的最大值.
变式训练
解析
(1)由,得,又
所以由,得,即
(2)由(1)知
所以
当 时 取得最大值,且最大值为4050平方米
典例讲解
例6、 某山顶每隔 2 小时测得的温度( ℃ ) 如下表:
(1) 以时刻 (单位:时 )为横坐标,气温 (单位:℃) 为纵坐标,画出散点图;
(2) 用正弦型曲线去拟合这些数据,写出 关于 的函数解析式.
时刻 0 2 4 6 8 10 12 14 16 18 20 22 24
气温 13.5 6 1 -2 1.4 5.9 14.1 22.5 27.5 28 27.3 21 14.5
思路解析
先画出散点图,再根据散点图探求 与 的函数关系式
典例讲解
(2)设气温 关于 的解析式为
则 解得 又周期
又当 时,
解析
散点图如图所示.
方法归纳
(1)拟合模型的组建
⒈拟合模型是通过对有关变量的观测, 对数据的观察、分析及选择恰当的数学表达方式而得到的. 它的实质是数据拟合的精度和表达式简化程度的折中,折中方案的选择取决于实际需要.
(2)拟合的主要方法
⒈经验拟合: 选择规律简单的数学表达式, 讨论变量间的内在规律, 允许存在一定的误差;
⒉插值拟合:要求精确拟合相关数据, 即在观测点之间插入适当的数值.
(3)拟合的步骤
⒈根据原始数据、表格绘出散点图
⒉通过散点图,画出“最贴近”的直线或曲线,即拟合直线或拟合曲线;
⒊根据所学的函数知识,求出拟合直线或拟合曲线的函数解析式;
⒋利用函数解析式,根据条件对所给问题进行预测和控制,以便为决策和管理提供依据.
变式训练
6.一般地,人的体温是时刻变化的. 下表中给出了在 24 h 期间某人的体温的典型变化 (从夜间零点开始计时)
(1) 作出这些数据的散点图
(2) 选用一个三角函数来近似描述这些数据
时间/h 温度/ ℃
0 36.8
2 36.7
4 36.6
6 36.7
8 36.8
10 37
12 37.2
时间/h 温度/℃
14 37.3
16 37.4
18 37.3
20 37.2
22 37
24 36.8
变式训练
解析
(2) 设 ,
则
由
得取
故可用函数来近似描述这些数据.
(1)设时间为 温度为 散点图如图 :
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
