第6课时 圆的面积的应用(课件)六年级上册数学人教版(共15张PPT)
文档属性
| 名称 | 第6课时 圆的面积的应用(课件)六年级上册数学人教版(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-12 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
6、圆面积的应用
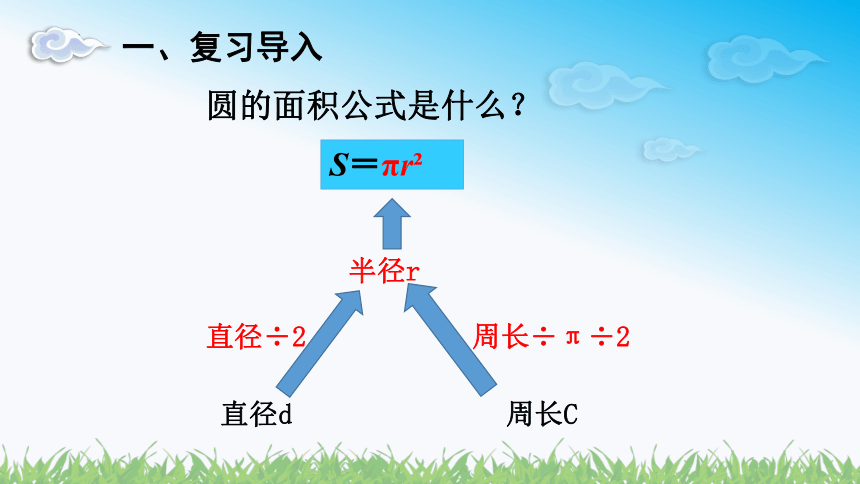
一、复习导入
圆的面积公式是什么?
S=πr
半径r
直径d
周长C
直径÷2
周长÷π÷2
二、巩固练习
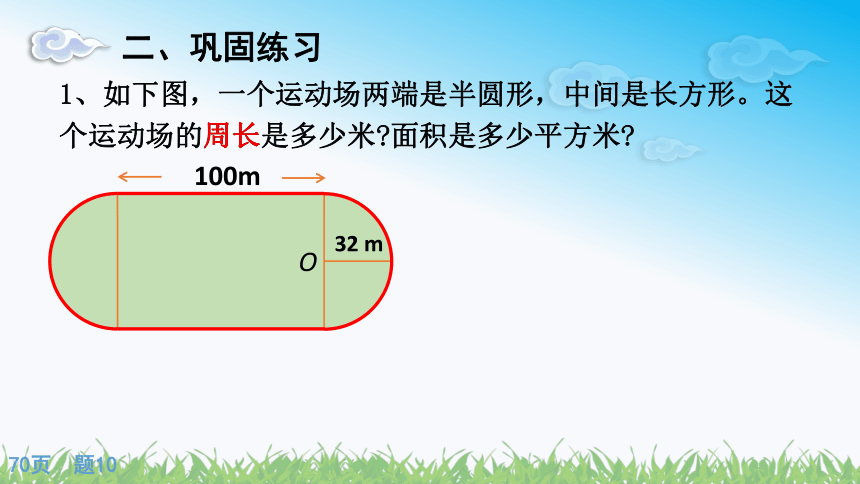
1、如下图,一个运动场两端是半圆形,中间是长方形。这个运动场的周长是多少米 面积是多少平方米
周长
O
32 m
100m
70页 题10
二、巩固练习
1、如下图,一个运动场两端是半圆形,中间是长方形。这个运动场的周长是多少米 面积是多少平方米
周长
O
32 m
100m
面积
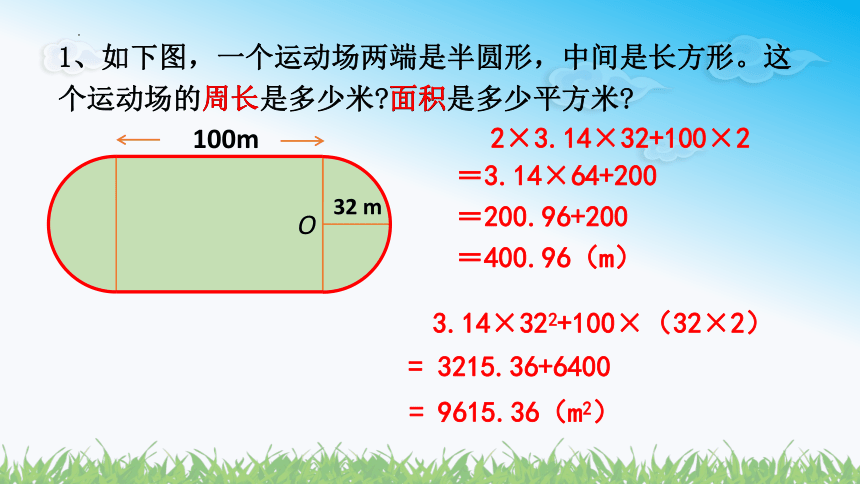
1、如下图,一个运动场两端是半圆形,中间是长方形。这个运动场的周长是多少米 面积是多少平方米
周长
O
32 m
100m
面积
2×3.14×32+100×2
=3.14×64+200
=200.96+200
=400.96(m)
3.14×322+100×(32×2)
= 3215.36+6400
= 9615.36(m2)
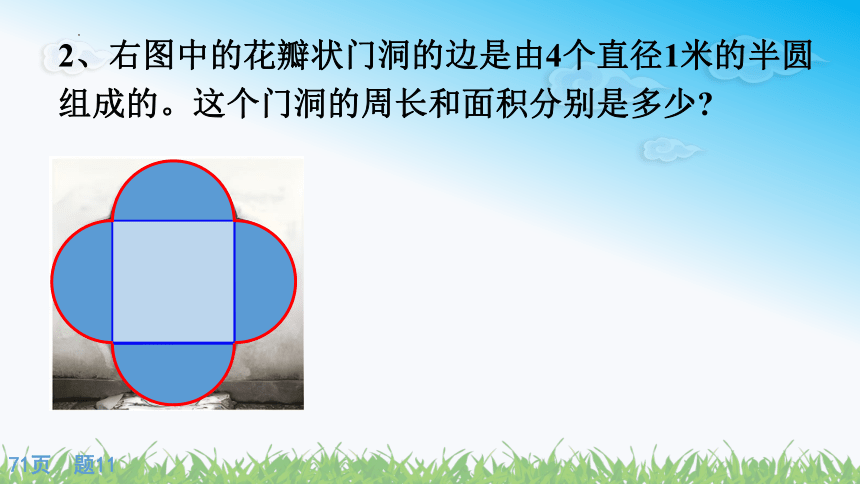
2、右图中的花瓣状门洞的边是由4个直径1米的半圆组成的。这个门洞的周长和面积分别是多少
71页 题11
2、右图中的花瓣状门洞的边是由4个直径1米的半圆组成的。这个门洞的周长和面积分别是多少
71页 题11
2、右图中的花瓣状门洞的边是由4个直径1米的半圆组成的。这个门洞的周长和面积分别是多少
71页 题11
周长:
C=πd×2
=3.14×1×2
=6.28(m)
面积:
S=2πr2+a2
=2×3.14×0.52+12
=2.57(m2)
答:这个门洞的周长是6.28米,
面积是2.57m2。
=1.57+1
3、如右图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少
能不能用“周长÷π÷2=半径”来求半径
不能,因为128.5m是半圆的周长
71页 题14
3、如右图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少
半圆周长=πr+2r
=(π+2)r
r=半圆周长÷(π+2)
128.5÷(3.14+2)=25(m)
3.14×252=3.14×625=1962.5(m2)
答:这两块草坪的总面积是1962.5平方米。
4、 有一栋底面呈长方形的建筑物(如下图),墙角有一根木桩,木桩上拴着一条狗。拴狗的绳子长4 m,这条狗活动区域的面积有多大
[教材P72 第17题]
墙
墙
r=4m
S阴=S圆×
3
4
3.14×42×
3
4
= 3.14×12
= 37.68(m2)
答:狗活动区域的面积为37.68平方米。
5、(1)一根绳子长31.4 m,用这根绳子在操场上围出一块地。怎样围面积最大 请你画一画,算一算。
[教材P72 题18]
学过哪些图形的面积?
周长相等时,哪个图形的面积最大?
3.14÷3.14÷2=5 (m)
3.14×52=78.5 (m2)
3.14÷4=7.85 (m)
7.85×7.85=61.6225 (m2)
3.14÷2=15.7(m)
设 a=10 m,b=5.7 m
S=πr2
S=a2
S=ab
10×5.7=57(m2)
S=ah
a
b
h
3.14÷2=15.7(m)
设 a=10 m,b=5.7 m,h<b<5.7
S<57(m2)
周长相等时,圆的面积是最大的。
(2)为什么草原上蒙古包的底面是圆形的 为什么绝大多数植物的根和茎的横截面是圆形的 根据上面的研究,请你试着解释一下。
蒙古包的底面是圆形的,与其他形状建筑物相比利用面积是最大的。绝大多数的根和茎的横截面是圆形的,利用面积最大,可以更好地吸收水分。
6、圆面积的应用
一、复习导入
圆的面积公式是什么?
S=πr
半径r
直径d
周长C
直径÷2
周长÷π÷2
二、巩固练习
1、如下图,一个运动场两端是半圆形,中间是长方形。这个运动场的周长是多少米 面积是多少平方米
周长
O
32 m
100m
70页 题10
二、巩固练习
1、如下图,一个运动场两端是半圆形,中间是长方形。这个运动场的周长是多少米 面积是多少平方米
周长
O
32 m
100m
面积
1、如下图,一个运动场两端是半圆形,中间是长方形。这个运动场的周长是多少米 面积是多少平方米
周长
O
32 m
100m
面积
2×3.14×32+100×2
=3.14×64+200
=200.96+200
=400.96(m)
3.14×322+100×(32×2)
= 3215.36+6400
= 9615.36(m2)
2、右图中的花瓣状门洞的边是由4个直径1米的半圆组成的。这个门洞的周长和面积分别是多少
71页 题11
2、右图中的花瓣状门洞的边是由4个直径1米的半圆组成的。这个门洞的周长和面积分别是多少
71页 题11
2、右图中的花瓣状门洞的边是由4个直径1米的半圆组成的。这个门洞的周长和面积分别是多少
71页 题11
周长:
C=πd×2
=3.14×1×2
=6.28(m)
面积:
S=2πr2+a2
=2×3.14×0.52+12
=2.57(m2)
答:这个门洞的周长是6.28米,
面积是2.57m2。
=1.57+1
3、如右图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少
能不能用“周长÷π÷2=半径”来求半径
不能,因为128.5m是半圆的周长
71页 题14
3、如右图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少
半圆周长=πr+2r
=(π+2)r
r=半圆周长÷(π+2)
128.5÷(3.14+2)=25(m)
3.14×252=3.14×625=1962.5(m2)
答:这两块草坪的总面积是1962.5平方米。
4、 有一栋底面呈长方形的建筑物(如下图),墙角有一根木桩,木桩上拴着一条狗。拴狗的绳子长4 m,这条狗活动区域的面积有多大
[教材P72 第17题]
墙
墙
r=4m
S阴=S圆×
3
4
3.14×42×
3
4
= 3.14×12
= 37.68(m2)
答:狗活动区域的面积为37.68平方米。
5、(1)一根绳子长31.4 m,用这根绳子在操场上围出一块地。怎样围面积最大 请你画一画,算一算。
[教材P72 题18]
学过哪些图形的面积?
周长相等时,哪个图形的面积最大?
3.14÷3.14÷2=5 (m)
3.14×52=78.5 (m2)
3.14÷4=7.85 (m)
7.85×7.85=61.6225 (m2)
3.14÷2=15.7(m)
设 a=10 m,b=5.7 m
S=πr2
S=a2
S=ab
10×5.7=57(m2)
S=ah
a
b
h
3.14÷2=15.7(m)
设 a=10 m,b=5.7 m,h<b<5.7
S<57(m2)
周长相等时,圆的面积是最大的。
(2)为什么草原上蒙古包的底面是圆形的 为什么绝大多数植物的根和茎的横截面是圆形的 根据上面的研究,请你试着解释一下。
蒙古包的底面是圆形的,与其他形状建筑物相比利用面积是最大的。绝大多数的根和茎的横截面是圆形的,利用面积最大,可以更好地吸收水分。
