人教版(2019)数学选择性必修第一册 第三章圆锥曲线的方程 章末复习导学案(含答案)
文档属性
| 名称 | 人教版(2019)数学选择性必修第一册 第三章圆锥曲线的方程 章末复习导学案(含答案) | 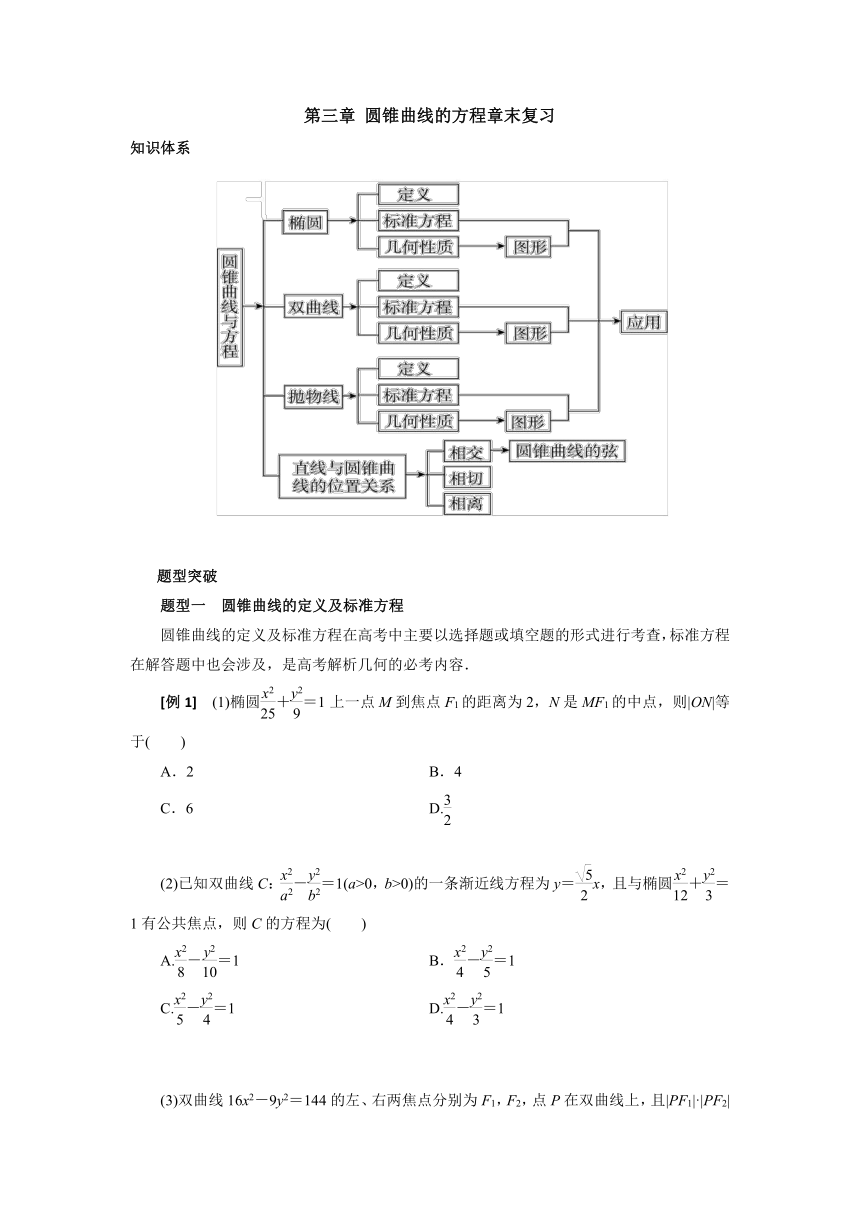 | |
| 格式 | docx | ||
| 文件大小 | 107.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-13 23:24:35 | ||
图片预览





文档简介
第三章 圆锥曲线的方程章末复习
知识体系
题型突破
题型一 圆锥曲线的定义及标准方程
圆锥曲线的定义及标准方程在高考中主要以选择题或填空题的形式进行考查,标准方程在解答题中也会涉及,是高考解析几何的必考内容.
[例1] (1)椭圆+=1上一点M到焦点F1的距离为2,N是MF1的中点,则|ON|等于( )
A.2 B.4
C.6 D.
(2)已知双曲线C:-=1(a>0,b>0)的一条渐近线方程为y=x,且与椭圆+=1有公共焦点,则C的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
(3)双曲线16x2-9y2=144的左、右两焦点分别为F1,F2,点P在双曲线上,且|PF1|·|PF2|=64,则∠F1PF2=________.
反思感悟
求圆锥曲线方程的一般步骤
一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤.
(1)定形——指的是二次曲线的焦点位置与对称轴的位置.
(2)定式——根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在哪个坐标轴上时,可设方程为mx2+ny2=1(m>0,n>0).
(3)定量——由题设中的条件找到“式”中待定系数的等量关系,通过解方程得到量的大小.
跟踪训练
1.若中心在坐标原点的椭圆的长轴长与短轴长之比为2,它的一个焦点是(2,0),则椭圆的标准方程是( )
A.+=1 B.+=1
C.+=1 D.+=1
2.已知P为抛物线y=x2上的动点,点P在x轴上的射影为Q,A,则|PA|+|PQ|的最小值是( )
A. B.
C. D.10
题型二 圆锥曲线的几何性质
圆锥曲线的几何性质是圆锥曲线的核心内容,高考非常重视对圆锥曲线几何性质的考查,试卷中一般以选择题或者填空题的形式考查圆锥曲线的几何性质(主要是椭圆和双曲线的离心率),在解答题中与圆锥曲线方程的其他知识一起进行综合考查.
[例2] (1)已知双曲线的渐近线方程为y=±x,则双曲线的离心率为( )
A. B.
C.或 D.
(2)已知椭圆+=1(a>b>0)的左顶点为A,上顶点为B,右焦点为F.设线段AB的中点为M,若2·+2≥0,则该椭圆的离心率的取值范围为( )
A.(0,-1] B.
C. D.(0,-1]
[反思感悟]
求解离心率三种方法
定义法 由椭圆(双曲线)的标准方程可知,不论椭圆(双曲线)的焦点在x轴上还是y轴上都有关系式a2-b2=c2(a2+b2=c2)以及e=,已知其中的任意两个参数,可以求其他的参数,这是基本且常用的方法
方程法 建立参数a与c之间的齐次关系式,从而求出其离心率,这是求离心率的十分重要的思路及方法
几何法 求与过焦点的三角形有关的离心率问题,根据平面几何性质以及椭圆(双曲线)的定义、几何性质,建立参数之间的关系,通过画出图形,观察线段之间的关系,使问题更形象、直观
跟踪训练
1.如果方程x2+ky2=2表示焦点在x轴上,且焦距为的椭圆,则椭圆的短轴长为________.
2.过双曲线-=1(a>0,b>0)的一个焦点且垂直于双曲线实轴的直线交双曲线于A,B两点.若以AB为直径的圆恰过双曲线的一个顶点,则双曲线的离心率是________.
3.已知双曲线-=1(a>0,b>0)的焦距为2c,右顶点为A,抛物线x2=2py(p>0)的焦点为F.若双曲线截抛物线的准线所得线段长为2c,且|FA|=c,则双曲线的渐近线方程为________.
题型三 直线与圆锥曲线的位置关系
高考试题中解析几何的解答题一般不会单纯考查圆锥曲线,试题中一般都有直线问题参与,这使得解析几何试题具有广泛的命题背景,当直线与圆锥曲线问题综合时就产生了如:直线与圆锥曲线的位置关系(相交、相切、相离),直线与曲线交汇产生的一些几何量的范围和最值,动直线(或曲线)过定点等一系列热点问题,这些热点问题都是高考所重视的.
[例3] 已知椭圆的一个顶点为A(0,-1),焦点在x轴上,若右焦点到直线x-y+2=0的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线y=kx+m(k≠0)相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围.
反思感悟
有关直线与圆锥曲线综合问题的求解方法
(1)将直线方程与圆锥曲线方程联立,化简后得到关于x(或y)的一元二次方程,则直线与圆锥曲线的位置关系有三种情况:
①相交:Δ>0 直线与椭圆相交;Δ>0 直线与双曲线相交,但直线与双曲线相交不一定有Δ>0,如当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故Δ>0是直线与双曲线相交的充分不必要条件;Δ>0 直线与抛物线相交,但直线与抛物线相交不一定有Δ>0,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故Δ>0也仅是直线与抛物线相交的充分条件,而不是必要条件.
②相切:Δ=0 直线与椭圆相切;Δ=0 直线与双曲线相切;Δ=0 直线与抛物线相切.
③相离:Δ<0 直线与椭圆相离;Δ<0 直线与双曲线相离;Δ<0 直线与抛物线相离.
(2)直线与圆锥曲线的位置关系,涉及函数、方程、不等式、平面几何等诸多方面的知识,形成了求轨迹、最值、对称、取值范围、线段的长度等多种问题.解决此类问题应注意数形结合,以形辅数的方法;还要多结合圆锥曲线的定义,根与系数的关系以及“点差法”等.
跟踪训练
1.直线l与抛物线C:y2=2x交于A,B两点,O为坐标原点,若直线OA,OB的斜率k1,k2满足k1k2=,则直线l过定点( )
A.(-3,0) B.(0,-3)
C.(3,0) D.(0,3)
2.平面直角坐标系xOy中,过椭圆M:+=1(a>b>0)右焦点的直线x+y-=0交M于A,B两点,P为AB的中点,且OP的斜率为.
(1)求M的方程;
(2)C,D为M上两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
参考答案
[例1] [解析] (1)设椭圆的另一个焦点为F2,因为椭圆+=1上一点M到焦点F1的距离为2,即|MF1|=2,又|MF1|+|MF2|=2a=10,所以|MF2|=8.因为N是MF1的中点,O是F1F2的中点,所以|ON|=|MF2|=4.
(2)根据双曲线C的渐近线方程为y=x,
可知=.①
又椭圆+=1的焦点坐标为(3,0)和(-3,0),
所以a2+b2=9.②
根据①②可知a2=4,b2=5,
所以C的方程为-=1.
(3)双曲线方程16x2-9y2=144
化简为-=1,
即a2=9,b2=16,所以c2=25,
解得a=3,c=5,所以F1(-5,0),F2(5,0).
设 |PF1|=m,|PF2|=n,
由双曲线的定义知|m-n|=2a=6,
又已知m·n=64,
在△PF1F2中,由余弦定理知
cos∠F1PF2=
==
==.
所以∠F1PF2=60°.
[答案] (1)B (2)B (3)60°
跟踪训练
1.解析:选D 不妨设椭圆的标准方程为+=1(a>b>0),依题意得,==2 a=2b,∵c=2,c2=a2-b2,∴(2)2=(2b)2-b2 b2=20,得a2=4b2=80,故所求椭圆的标准方程为+=1.
2.解析:选C 抛物线的准线方程为y=-.设抛物线的焦点为F,则F.根据抛物线的定义可得|PQ|=|PF|-,所以|PA|+|PQ|=|PF|+|PA|-.所以|PA|+|PQ|的最小值为|FA|-=.
[例2] [解析] (1)由双曲线的渐近线方程为y=±x,
得=或=,又离心率e=,
所以e=或e=.
(2)因为A(-a,0),B(0,b),M,F(c,0),
所以=,=,
=(c,-b),又2·+2≥0,
所以2a2-2ac-c2≥0,即e2+2e-2≤0,
结合0<e<1得0<e≤-1.
[答案] (1)C (2)A
跟踪训练
1.解析:方程x2+ky2=2可化为+=1,则2+=2 =,∴短轴长为2×=.
答案:
2.解析:设双曲线的左顶点为P,A位于第一象限,B位于第四象限,把x=c代入双曲线方程-=1,得到|AF|=yA=,又|PF|=c+a,依题意知|AF|=|PF|,∴=c+a b2=ac+a2,又b2=c2-a2,∴c2-a2=ac+a2,两边同除以a2得到2--2=0 e2-e-2=0,又∵e>1,∴e=2.
答案:2
3.解析:c2=a2+b2,①
由双曲线截抛物线的准线所得线段长为2c知,
双曲线过点,即-=1.②
由|FA|=c,得c2=a2+,③
由①③得p2=4b2.④
将④代入②,得=2.
∴=2,即=1,
故双曲线的渐近线方程为y=±x,即x±y=0.
答案:x±y=0
[例3] [解] (1)依题意可设椭圆方程为+y2=1(a>1),
则右焦点F(,0),
由题设,知=3,
解得a2=3,故所求椭圆的方程为+y2=1.
(2)设点P为弦MN的中点,由
得(3k2+1)x2+6mkx+3(m2-1)=0,
由于直线与椭圆有两个交点,
所以Δ>0,即m2<3k2+1, ①
所以xP==-,
从而yP=kxP+m=,
所以kAP==-,
又|AM|=|AN|,所以AP⊥MN,
则-=-,即2m=3k2+1, ②
把②代入①得2m>m2,
解得0由②得k2=>0,
解得m>,
故所求m的取值范围是.
跟踪训练
1.解析:选A 设直线l的方程为x=my+b,
A(x1,y1),B(x2,y2),
因为k1k2=,所以·=.
又y=2x1,y=2x2,所以y1y2=6.
将直线l:x=my+b代入抛物线C:y2=2x得
y2-2my-2b=0,
所以y1y2=-2b=6,所以b=-3,
即直线l:x=my-3,所以直线l过定点(-3,0).
2.解:(1)设A(x1,y1),B(x2,y2),P(x0,y0),则
+=1,+=1,=-1,
由此可得=-=1.
因为x1+x2=2x0,y1+y2=2y0,=,
所以a2=2b2.
又由题意知,M的右焦点为(,0),故a2-b2=3.
因此a2=6,b2=3.
所以M的方程为+=1.
(2)由解得或
因此|AB|=.
由题意可设直线CD的方程为
y=x+n,
设C(x3,y3),D(x4,y4).
由得3x2+4nx+2n2-6=0.
于是x3,4=.
因为直线CD的斜率为1,
所以|CD|=|x4-x3|= .
由已知,四边形ACBD的面积S=|CD|·|AB|= .
当n=0时,S取得最大值,最大值为.
所以四边形ACBD面积的最大值为.
知识体系
题型突破
题型一 圆锥曲线的定义及标准方程
圆锥曲线的定义及标准方程在高考中主要以选择题或填空题的形式进行考查,标准方程在解答题中也会涉及,是高考解析几何的必考内容.
[例1] (1)椭圆+=1上一点M到焦点F1的距离为2,N是MF1的中点,则|ON|等于( )
A.2 B.4
C.6 D.
(2)已知双曲线C:-=1(a>0,b>0)的一条渐近线方程为y=x,且与椭圆+=1有公共焦点,则C的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
(3)双曲线16x2-9y2=144的左、右两焦点分别为F1,F2,点P在双曲线上,且|PF1|·|PF2|=64,则∠F1PF2=________.
反思感悟
求圆锥曲线方程的一般步骤
一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤.
(1)定形——指的是二次曲线的焦点位置与对称轴的位置.
(2)定式——根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在哪个坐标轴上时,可设方程为mx2+ny2=1(m>0,n>0).
(3)定量——由题设中的条件找到“式”中待定系数的等量关系,通过解方程得到量的大小.
跟踪训练
1.若中心在坐标原点的椭圆的长轴长与短轴长之比为2,它的一个焦点是(2,0),则椭圆的标准方程是( )
A.+=1 B.+=1
C.+=1 D.+=1
2.已知P为抛物线y=x2上的动点,点P在x轴上的射影为Q,A,则|PA|+|PQ|的最小值是( )
A. B.
C. D.10
题型二 圆锥曲线的几何性质
圆锥曲线的几何性质是圆锥曲线的核心内容,高考非常重视对圆锥曲线几何性质的考查,试卷中一般以选择题或者填空题的形式考查圆锥曲线的几何性质(主要是椭圆和双曲线的离心率),在解答题中与圆锥曲线方程的其他知识一起进行综合考查.
[例2] (1)已知双曲线的渐近线方程为y=±x,则双曲线的离心率为( )
A. B.
C.或 D.
(2)已知椭圆+=1(a>b>0)的左顶点为A,上顶点为B,右焦点为F.设线段AB的中点为M,若2·+2≥0,则该椭圆的离心率的取值范围为( )
A.(0,-1] B.
C. D.(0,-1]
[反思感悟]
求解离心率三种方法
定义法 由椭圆(双曲线)的标准方程可知,不论椭圆(双曲线)的焦点在x轴上还是y轴上都有关系式a2-b2=c2(a2+b2=c2)以及e=,已知其中的任意两个参数,可以求其他的参数,这是基本且常用的方法
方程法 建立参数a与c之间的齐次关系式,从而求出其离心率,这是求离心率的十分重要的思路及方法
几何法 求与过焦点的三角形有关的离心率问题,根据平面几何性质以及椭圆(双曲线)的定义、几何性质,建立参数之间的关系,通过画出图形,观察线段之间的关系,使问题更形象、直观
跟踪训练
1.如果方程x2+ky2=2表示焦点在x轴上,且焦距为的椭圆,则椭圆的短轴长为________.
2.过双曲线-=1(a>0,b>0)的一个焦点且垂直于双曲线实轴的直线交双曲线于A,B两点.若以AB为直径的圆恰过双曲线的一个顶点,则双曲线的离心率是________.
3.已知双曲线-=1(a>0,b>0)的焦距为2c,右顶点为A,抛物线x2=2py(p>0)的焦点为F.若双曲线截抛物线的准线所得线段长为2c,且|FA|=c,则双曲线的渐近线方程为________.
题型三 直线与圆锥曲线的位置关系
高考试题中解析几何的解答题一般不会单纯考查圆锥曲线,试题中一般都有直线问题参与,这使得解析几何试题具有广泛的命题背景,当直线与圆锥曲线问题综合时就产生了如:直线与圆锥曲线的位置关系(相交、相切、相离),直线与曲线交汇产生的一些几何量的范围和最值,动直线(或曲线)过定点等一系列热点问题,这些热点问题都是高考所重视的.
[例3] 已知椭圆的一个顶点为A(0,-1),焦点在x轴上,若右焦点到直线x-y+2=0的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线y=kx+m(k≠0)相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围.
反思感悟
有关直线与圆锥曲线综合问题的求解方法
(1)将直线方程与圆锥曲线方程联立,化简后得到关于x(或y)的一元二次方程,则直线与圆锥曲线的位置关系有三种情况:
①相交:Δ>0 直线与椭圆相交;Δ>0 直线与双曲线相交,但直线与双曲线相交不一定有Δ>0,如当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故Δ>0是直线与双曲线相交的充分不必要条件;Δ>0 直线与抛物线相交,但直线与抛物线相交不一定有Δ>0,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故Δ>0也仅是直线与抛物线相交的充分条件,而不是必要条件.
②相切:Δ=0 直线与椭圆相切;Δ=0 直线与双曲线相切;Δ=0 直线与抛物线相切.
③相离:Δ<0 直线与椭圆相离;Δ<0 直线与双曲线相离;Δ<0 直线与抛物线相离.
(2)直线与圆锥曲线的位置关系,涉及函数、方程、不等式、平面几何等诸多方面的知识,形成了求轨迹、最值、对称、取值范围、线段的长度等多种问题.解决此类问题应注意数形结合,以形辅数的方法;还要多结合圆锥曲线的定义,根与系数的关系以及“点差法”等.
跟踪训练
1.直线l与抛物线C:y2=2x交于A,B两点,O为坐标原点,若直线OA,OB的斜率k1,k2满足k1k2=,则直线l过定点( )
A.(-3,0) B.(0,-3)
C.(3,0) D.(0,3)
2.平面直角坐标系xOy中,过椭圆M:+=1(a>b>0)右焦点的直线x+y-=0交M于A,B两点,P为AB的中点,且OP的斜率为.
(1)求M的方程;
(2)C,D为M上两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
参考答案
[例1] [解析] (1)设椭圆的另一个焦点为F2,因为椭圆+=1上一点M到焦点F1的距离为2,即|MF1|=2,又|MF1|+|MF2|=2a=10,所以|MF2|=8.因为N是MF1的中点,O是F1F2的中点,所以|ON|=|MF2|=4.
(2)根据双曲线C的渐近线方程为y=x,
可知=.①
又椭圆+=1的焦点坐标为(3,0)和(-3,0),
所以a2+b2=9.②
根据①②可知a2=4,b2=5,
所以C的方程为-=1.
(3)双曲线方程16x2-9y2=144
化简为-=1,
即a2=9,b2=16,所以c2=25,
解得a=3,c=5,所以F1(-5,0),F2(5,0).
设 |PF1|=m,|PF2|=n,
由双曲线的定义知|m-n|=2a=6,
又已知m·n=64,
在△PF1F2中,由余弦定理知
cos∠F1PF2=
==
==.
所以∠F1PF2=60°.
[答案] (1)B (2)B (3)60°
跟踪训练
1.解析:选D 不妨设椭圆的标准方程为+=1(a>b>0),依题意得,==2 a=2b,∵c=2,c2=a2-b2,∴(2)2=(2b)2-b2 b2=20,得a2=4b2=80,故所求椭圆的标准方程为+=1.
2.解析:选C 抛物线的准线方程为y=-.设抛物线的焦点为F,则F.根据抛物线的定义可得|PQ|=|PF|-,所以|PA|+|PQ|=|PF|+|PA|-.所以|PA|+|PQ|的最小值为|FA|-=.
[例2] [解析] (1)由双曲线的渐近线方程为y=±x,
得=或=,又离心率e=,
所以e=或e=.
(2)因为A(-a,0),B(0,b),M,F(c,0),
所以=,=,
=(c,-b),又2·+2≥0,
所以2a2-2ac-c2≥0,即e2+2e-2≤0,
结合0<e<1得0<e≤-1.
[答案] (1)C (2)A
跟踪训练
1.解析:方程x2+ky2=2可化为+=1,则2+=2 =,∴短轴长为2×=.
答案:
2.解析:设双曲线的左顶点为P,A位于第一象限,B位于第四象限,把x=c代入双曲线方程-=1,得到|AF|=yA=,又|PF|=c+a,依题意知|AF|=|PF|,∴=c+a b2=ac+a2,又b2=c2-a2,∴c2-a2=ac+a2,两边同除以a2得到2--2=0 e2-e-2=0,又∵e>1,∴e=2.
答案:2
3.解析:c2=a2+b2,①
由双曲线截抛物线的准线所得线段长为2c知,
双曲线过点,即-=1.②
由|FA|=c,得c2=a2+,③
由①③得p2=4b2.④
将④代入②,得=2.
∴=2,即=1,
故双曲线的渐近线方程为y=±x,即x±y=0.
答案:x±y=0
[例3] [解] (1)依题意可设椭圆方程为+y2=1(a>1),
则右焦点F(,0),
由题设,知=3,
解得a2=3,故所求椭圆的方程为+y2=1.
(2)设点P为弦MN的中点,由
得(3k2+1)x2+6mkx+3(m2-1)=0,
由于直线与椭圆有两个交点,
所以Δ>0,即m2<3k2+1, ①
所以xP==-,
从而yP=kxP+m=,
所以kAP==-,
又|AM|=|AN|,所以AP⊥MN,
则-=-,即2m=3k2+1, ②
把②代入①得2m>m2,
解得0
解得m>,
故所求m的取值范围是.
跟踪训练
1.解析:选A 设直线l的方程为x=my+b,
A(x1,y1),B(x2,y2),
因为k1k2=,所以·=.
又y=2x1,y=2x2,所以y1y2=6.
将直线l:x=my+b代入抛物线C:y2=2x得
y2-2my-2b=0,
所以y1y2=-2b=6,所以b=-3,
即直线l:x=my-3,所以直线l过定点(-3,0).
2.解:(1)设A(x1,y1),B(x2,y2),P(x0,y0),则
+=1,+=1,=-1,
由此可得=-=1.
因为x1+x2=2x0,y1+y2=2y0,=,
所以a2=2b2.
又由题意知,M的右焦点为(,0),故a2-b2=3.
因此a2=6,b2=3.
所以M的方程为+=1.
(2)由解得或
因此|AB|=.
由题意可设直线CD的方程为
y=x+n,
设C(x3,y3),D(x4,y4).
由得3x2+4nx+2n2-6=0.
于是x3,4=.
因为直线CD的斜率为1,
所以|CD|=|x4-x3|= .
由已知,四边形ACBD的面积S=|CD|·|AB|= .
当n=0时,S取得最大值,最大值为.
所以四边形ACBD面积的最大值为.
