人教版(2019)数学选择性必修第一册 第一章 空间向量与立体几何 章末复习导学案(含答案)
文档属性
| 名称 | 人教版(2019)数学选择性必修第一册 第一章 空间向量与立体几何 章末复习导学案(含答案) | 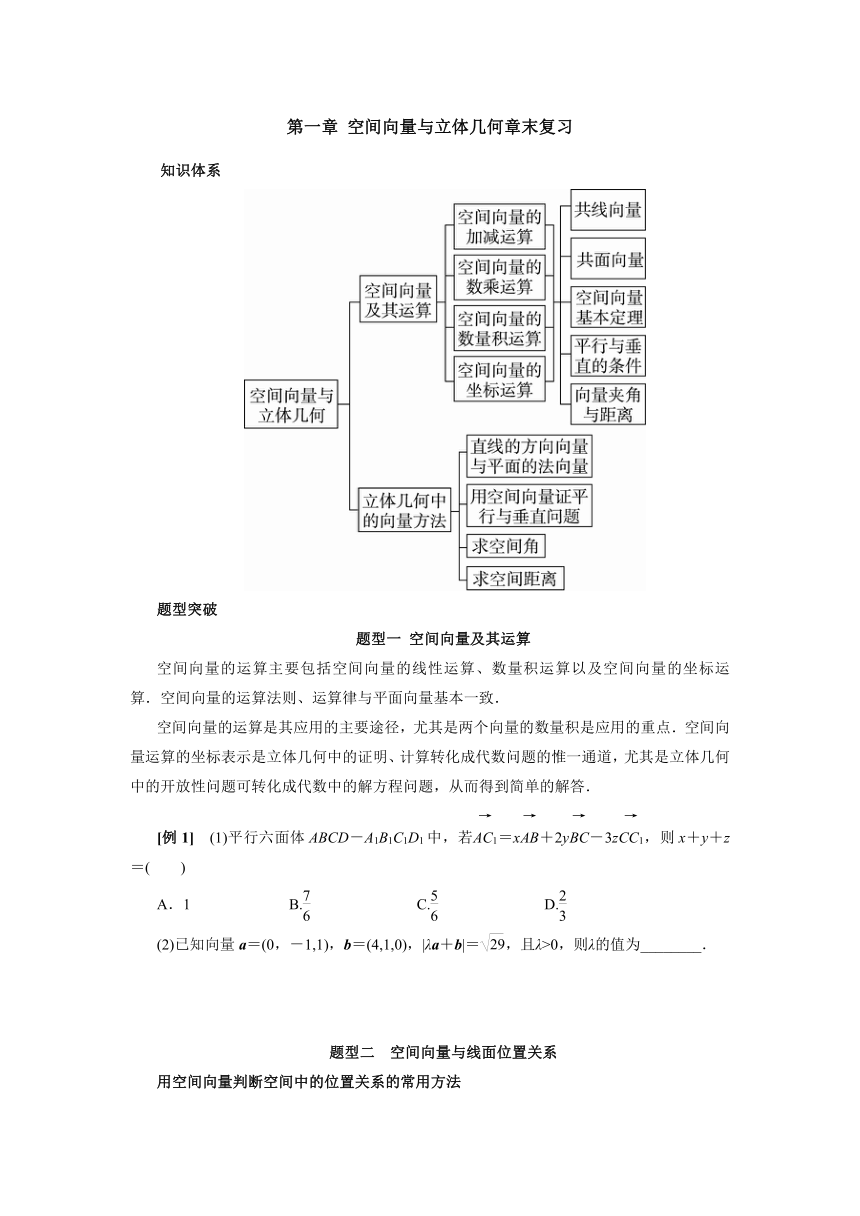 | |
| 格式 | docx | ||
| 文件大小 | 184.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-13 23:25:10 | ||
图片预览




文档简介
第一章 空间向量与立体几何章末复习
知识体系
题型突破
题型一 空间向量及其运算
空间向量的运算主要包括空间向量的线性运算、数量积运算以及空间向量的坐标运算.空间向量的运算法则、运算律与平面向量基本一致.
空间向量的运算是其应用的主要途径,尤其是两个向量的数量积是应用的重点.空间向量运算的坐标表示是立体几何中的证明、计算转化成代数问题的惟一通道,尤其是立体几何中的开放性问题可转化成代数中的解方程问题,从而得到简单的解答.
[例1] (1)平行六面体ABCD-A1B1C1D1中,若=x+2y-3z,则x+y+z=( )
A.1 B. C. D.
(2)已知向量a=(0,-1,1),b=(4,1,0),|λa+b|=,且λ>0,则λ的值为________.
题型二 空间向量与线面位置关系
用空间向量判断空间中的位置关系的常用方法
(1)线线平行.证明两条直线平行,只需证明两条直线的方向向量是共线向量.
(2)线线垂直.
证明两条直线垂直,只需证明两条直线的方向向量垂直.
(3)线面平行.
用向量证明线面平行的方法主要有:
①证明直线的方向向量与平面的法向量垂直;
②证明可在平面内找到一个向量与直线的方向向量是共线向量.
(4)线面垂直.
用向量证明线面垂直的方法主要有:
①证明直线的方向向量与平面的法向量平行;
②利用线面垂直的判定定理转化为线线垂直问题.
(5)面面平行.
①证明两个平面的法向量平行(即是共线向量);
②转化为线面平行、线线平行问题.
(6)面面垂直.
①证明两个平面的法向量互相垂直;
②转化为线面垂直、线线垂直问题.
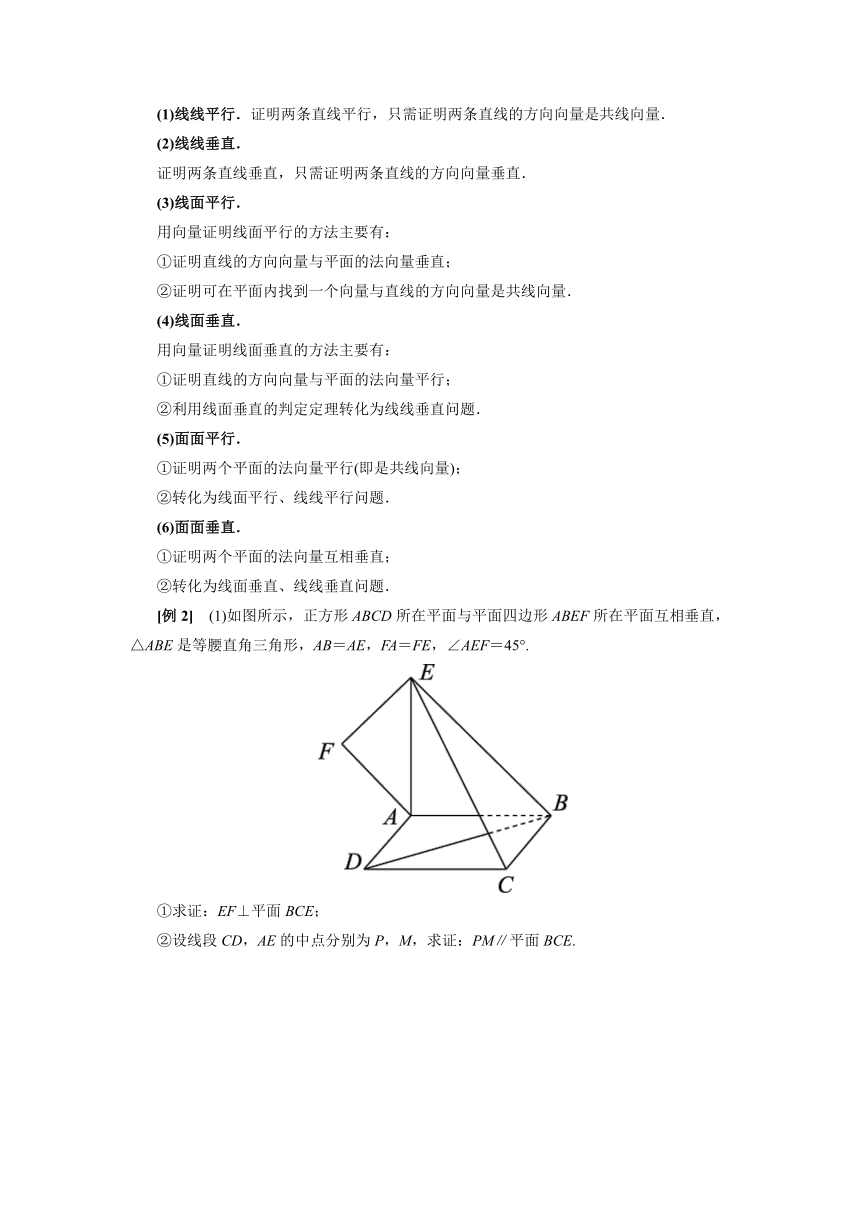
[例2] (1)如图所示,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
①求证:EF⊥平面BCE;
②设线段CD,AE的中点分别为P,M,求证:PM∥平面BCE.
(2)如图,已知四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,且PD=2.
①若点E,F分别在棱PB,AD上,且=4,=4,求证:EF⊥平面PBC;
②若点G在线段PA上,且三棱锥G-PBC的体积为,试求线段PG的长.
题型三 空间向量与空间角、用空间向量求空间角的方法
(1)若异面直线l1和l2的方向向量分别为v1和v2,它们所成的角为θ,则cos θ=|cos|.
(2)利用空间向量求直线与平面所成的角,可以有两种方法:一是分别求出斜线和它在平面内的射影所在直线的方向向量,将问题转化为求两个方向向量的夹角(或其补角);二是通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,则其余角就是斜线和平面所成的角.
(3)利用空间向量求二面角也可以有两种方法:一是分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的平面角的大小;二是通过平面的法向量来求,设二面角的两个半平面的法向量分别为n1和n2,则二面角的大小等于(或π-).
利用空间向量求二面角时,注意结合图形判断二面角是锐角还是钝角.
[例3] 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1所成二面角的正弦值.
[反思感悟] 运用向量法求空间的角(异面直线所成的角、线面角、二面角),都是转化为求两向量的夹角,其计算公式是两向量的数量积,体现了转化与化归的数学思想.
题型四 空间向量与空间距离
空间中的距离包括点点距、点线距、点面距、线线距、线面距、面面距,其中以点点距和点面距较为常见,其他的可转化为点点距、点面距来求,求解方法有传统的几何法、等积法和向量法.
[例4] (1) 已知矩形ABCD中,AB=,AD=1,将△ABD沿BD折起,使点A在平面BCD内的射影落在DC上,E,F,G分别为BD,AD,AB的中点.
①求证:DA⊥平面ABC;
②求点C到平面ABD的距离.
[反思感悟]
利用向量法求点面距时,注意d=,即求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即得出距离.
参考答案
[例1] (1) 答案: B
解析: 在平行六面体ABCD-A1B1C1D1中有=++.
又由=x+2y-3z=x+2y-3z,
可得x=1,y=,z=-,则x+y+z=.
(2) 答案:3
解析:解法一:由|λa+b|=,得
λ2|a|2+ |b|2+2λa·b=29, ①
又|a|==,
|b|==,
a·b=(0,-1,1)·(4,1,0)
=0×4+(-1)×1+1×0
=-1,
代入①得2λ2-2λ+17=29,
即λ2-λ-6=0,
解得λ=3或λ=-2,
又λ>0,∴λ=3.
解法二:由于a=(0,-1,1),b=(4,1,0).
所以λa+b=λ(0,-1,1)+(4,1,0)=(4,1-λ,λ),
又|λa+b|=,
∴42+(1-λ)2+λ2=29,
整理得λ2-λ-6=0,
解得λ=3或λ=-2,
又∵λ>0,∴λ=3.
[例2] (1)证明: ∵△ABE是等腰直角三角形,
∴AB=AE,AE⊥AB.
又∵平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,∴AE⊥平面ABCD,
∴AE⊥AD,即AD,AB,AE两两垂直,故建立如图所示的空间直角坐标系.
设AB=1,则AE=1,B(0,1,0),D(1,0,0),E(0,0,1),C(1,1,0).
①∵FA=FE,∠AEF=45°,
∴∠AFE=90°,从而F,
=,=(0,-1,1),=(1,0,0),
于是·=0,·=0.
∴EF⊥BE,EF⊥BC.
∵BE 平面BCE,BC 平面BCE,BC∩BE=B,
∴EF⊥平面BCE.
②由题意,得M,P,
从而=,
于是·=·=0+-=0,
∴PM⊥EF,
又EF⊥平面BCE,直线PM不在平面BCE内,
∴PM∥平面BCE.
(2) 解析: ①证明:以点D为坐标原点,DA为x轴正方向,DC为y轴正方向,DP为z轴正方向,建立空间直角坐标系.
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),P(0,0,2),
因为=4,=4,
所以F,E,
则=,=(-1,0,0).
·=0,同理·=0,
即EF垂直于平面PBC中两条相交直线,
所以EF⊥平面PBC.
②=(1,0,-2),可设=λ(0≤λ≤1),
所以向量的坐标为(λ,0,-2λ),
平面PBC的法向量为=,
点G到平面PBC的距离d===.
△PBC中,BC=1,PC=,PB=,
所以S△PBC=.
三棱锥G-PBC的体积V=S△PBC·d=××==,
所以λ=.
此时向量的坐标为,||=,
即线段PG的长为.
[例3] 解析:(1) 以A为坐标原点,建立如图所示的空间直角坐标系Axyz.
则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4),
所以=(2,0,-4),=(1,-1,-4).
因为cos<,>===,
所以异面直线A1B与C1D所成角的余弦值为.
(2) 设平面ADC1的一个法向量为n1=(x,y,z),
因为=(1,1,0),=(0,2,4),
所以n1·=0,n1·=0,
即x+y=0且y+2z=0,
取z=1,得x=2,y=-2.
所以,n1=(2,-2,1)是平面ADC1的一个法向量.
取平面ABA1的一个法向量为n2=(0,1,0),
设平面ADC1与平面ABA1所成二面角的大小为θ.
由|cos θ|===,得sin θ= .
因此,平面ADC1与平面ABA1所成二面角的正弦值为.
[例4]
解析:如图,以CB所在直线为x轴,DC所在直线为y轴,过点C,平面BDC方向向上的法向量为z轴建立空间直角坐标系,则C(0,0,0),A,B(1,0,0),D(0,-,0),E,F,G.
①证明:∵=,=,=(1,0,0),
且·=0-+=0,·=0+0+0=0,BA∩CB=B,
∴DA⊥平面ABC.
②设点C到平面ABD的距离为d.
由=,=,
容易求出平面ABD的一个法向量为n2=(-,1,-1),
∵=,
∴d=|||cos<,n2>|==.
即点C到平面ABD的距离为.
知识体系
题型突破
题型一 空间向量及其运算
空间向量的运算主要包括空间向量的线性运算、数量积运算以及空间向量的坐标运算.空间向量的运算法则、运算律与平面向量基本一致.
空间向量的运算是其应用的主要途径,尤其是两个向量的数量积是应用的重点.空间向量运算的坐标表示是立体几何中的证明、计算转化成代数问题的惟一通道,尤其是立体几何中的开放性问题可转化成代数中的解方程问题,从而得到简单的解答.
[例1] (1)平行六面体ABCD-A1B1C1D1中,若=x+2y-3z,则x+y+z=( )
A.1 B. C. D.
(2)已知向量a=(0,-1,1),b=(4,1,0),|λa+b|=,且λ>0,则λ的值为________.
题型二 空间向量与线面位置关系
用空间向量判断空间中的位置关系的常用方法
(1)线线平行.证明两条直线平行,只需证明两条直线的方向向量是共线向量.
(2)线线垂直.
证明两条直线垂直,只需证明两条直线的方向向量垂直.
(3)线面平行.
用向量证明线面平行的方法主要有:
①证明直线的方向向量与平面的法向量垂直;
②证明可在平面内找到一个向量与直线的方向向量是共线向量.
(4)线面垂直.
用向量证明线面垂直的方法主要有:
①证明直线的方向向量与平面的法向量平行;
②利用线面垂直的判定定理转化为线线垂直问题.
(5)面面平行.
①证明两个平面的法向量平行(即是共线向量);
②转化为线面平行、线线平行问题.
(6)面面垂直.
①证明两个平面的法向量互相垂直;
②转化为线面垂直、线线垂直问题.
[例2] (1)如图所示,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
①求证:EF⊥平面BCE;
②设线段CD,AE的中点分别为P,M,求证:PM∥平面BCE.
(2)如图,已知四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,且PD=2.
①若点E,F分别在棱PB,AD上,且=4,=4,求证:EF⊥平面PBC;
②若点G在线段PA上,且三棱锥G-PBC的体积为,试求线段PG的长.
题型三 空间向量与空间角、用空间向量求空间角的方法
(1)若异面直线l1和l2的方向向量分别为v1和v2,它们所成的角为θ,则cos θ=|cos
(2)利用空间向量求直线与平面所成的角,可以有两种方法:一是分别求出斜线和它在平面内的射影所在直线的方向向量,将问题转化为求两个方向向量的夹角(或其补角);二是通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,则其余角就是斜线和平面所成的角.
(3)利用空间向量求二面角也可以有两种方法:一是分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的平面角的大小;二是通过平面的法向量来求,设二面角的两个半平面的法向量分别为n1和n2,则二面角的大小等于
利用空间向量求二面角时,注意结合图形判断二面角是锐角还是钝角.
[例3] 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1所成二面角的正弦值.
[反思感悟] 运用向量法求空间的角(异面直线所成的角、线面角、二面角),都是转化为求两向量的夹角,其计算公式是两向量的数量积,体现了转化与化归的数学思想.
题型四 空间向量与空间距离
空间中的距离包括点点距、点线距、点面距、线线距、线面距、面面距,其中以点点距和点面距较为常见,其他的可转化为点点距、点面距来求,求解方法有传统的几何法、等积法和向量法.
[例4] (1) 已知矩形ABCD中,AB=,AD=1,将△ABD沿BD折起,使点A在平面BCD内的射影落在DC上,E,F,G分别为BD,AD,AB的中点.
①求证:DA⊥平面ABC;
②求点C到平面ABD的距离.
[反思感悟]
利用向量法求点面距时,注意d=,即求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即得出距离.
参考答案
[例1] (1) 答案: B
解析: 在平行六面体ABCD-A1B1C1D1中有=++.
又由=x+2y-3z=x+2y-3z,
可得x=1,y=,z=-,则x+y+z=.
(2) 答案:3
解析:解法一:由|λa+b|=,得
λ2|a|2+ |b|2+2λa·b=29, ①
又|a|==,
|b|==,
a·b=(0,-1,1)·(4,1,0)
=0×4+(-1)×1+1×0
=-1,
代入①得2λ2-2λ+17=29,
即λ2-λ-6=0,
解得λ=3或λ=-2,
又λ>0,∴λ=3.
解法二:由于a=(0,-1,1),b=(4,1,0).
所以λa+b=λ(0,-1,1)+(4,1,0)=(4,1-λ,λ),
又|λa+b|=,
∴42+(1-λ)2+λ2=29,
整理得λ2-λ-6=0,
解得λ=3或λ=-2,
又∵λ>0,∴λ=3.
[例2] (1)证明: ∵△ABE是等腰直角三角形,
∴AB=AE,AE⊥AB.
又∵平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,∴AE⊥平面ABCD,
∴AE⊥AD,即AD,AB,AE两两垂直,故建立如图所示的空间直角坐标系.
设AB=1,则AE=1,B(0,1,0),D(1,0,0),E(0,0,1),C(1,1,0).
①∵FA=FE,∠AEF=45°,
∴∠AFE=90°,从而F,
=,=(0,-1,1),=(1,0,0),
于是·=0,·=0.
∴EF⊥BE,EF⊥BC.
∵BE 平面BCE,BC 平面BCE,BC∩BE=B,
∴EF⊥平面BCE.
②由题意,得M,P,
从而=,
于是·=·=0+-=0,
∴PM⊥EF,
又EF⊥平面BCE,直线PM不在平面BCE内,
∴PM∥平面BCE.
(2) 解析: ①证明:以点D为坐标原点,DA为x轴正方向,DC为y轴正方向,DP为z轴正方向,建立空间直角坐标系.
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),P(0,0,2),
因为=4,=4,
所以F,E,
则=,=(-1,0,0).
·=0,同理·=0,
即EF垂直于平面PBC中两条相交直线,
所以EF⊥平面PBC.
②=(1,0,-2),可设=λ(0≤λ≤1),
所以向量的坐标为(λ,0,-2λ),
平面PBC的法向量为=,
点G到平面PBC的距离d===.
△PBC中,BC=1,PC=,PB=,
所以S△PBC=.
三棱锥G-PBC的体积V=S△PBC·d=××==,
所以λ=.
此时向量的坐标为,||=,
即线段PG的长为.
[例3] 解析:(1) 以A为坐标原点,建立如图所示的空间直角坐标系Axyz.
则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4),
所以=(2,0,-4),=(1,-1,-4).
因为cos<,>===,
所以异面直线A1B与C1D所成角的余弦值为.
(2) 设平面ADC1的一个法向量为n1=(x,y,z),
因为=(1,1,0),=(0,2,4),
所以n1·=0,n1·=0,
即x+y=0且y+2z=0,
取z=1,得x=2,y=-2.
所以,n1=(2,-2,1)是平面ADC1的一个法向量.
取平面ABA1的一个法向量为n2=(0,1,0),
设平面ADC1与平面ABA1所成二面角的大小为θ.
由|cos θ|===,得sin θ= .
因此,平面ADC1与平面ABA1所成二面角的正弦值为.
[例4]
解析:如图,以CB所在直线为x轴,DC所在直线为y轴,过点C,平面BDC方向向上的法向量为z轴建立空间直角坐标系,则C(0,0,0),A,B(1,0,0),D(0,-,0),E,F,G.
①证明:∵=,=,=(1,0,0),
且·=0-+=0,·=0+0+0=0,BA∩CB=B,
∴DA⊥平面ABC.
②设点C到平面ABD的距离为d.
由=,=,
容易求出平面ABD的一个法向量为n2=(-,1,-1),
∵=,
∴d=|||cos<,n2>|==.
即点C到平面ABD的距离为.
