人教版(2019)数学选择性必修第一册综合复习:抛物线学案(含答案)
文档属性
| 名称 | 人教版(2019)数学选择性必修第一册综合复习:抛物线学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 104.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 10:51:06 | ||
图片预览



文档简介
抛物线
新课程标准 考向预测
1.了解抛物线的实际背景,感受抛物线在刻画现实世界和解决实际问题中的应用. 2.了解抛物线的定义、几何图形和标准方程,以及它的简单几何性质. 3.通过抛物线的学习,进一步体会数形结合的思想. 4.了解抛物线的简单应用. 命题角度 1.抛物线的定义及应用 2.抛物线的标准方程与几何性质 3.直线与抛物线的位置关系
核心素养 数学运算、运算推理、直观想象
【基础梳理】
基础点一 抛物线的定义与标准方程
1.抛物线的定义:平面内到一个定点F和一条定直线l(l不经过定点F)____________的点的轨迹是抛物线.定点F叫做抛物线的________,定直线l叫做抛物线的________.
2.抛物线的标准方程
(1)焦参数为p,焦点在x轴正半轴上的抛物线的标准方程是____________________;
(2)焦参数为p,焦点在x轴负半轴上的抛物线的标准方程是____________________;
(3)焦参数为p,焦点在y轴正半轴上的抛物线的标准方程是____________________;
(4)焦参数为p,焦点在y轴负半轴上的抛物线的标准方程是____________________.
焦参数p的几何意义:焦点F到准线l的距离.
必记结论:当抛物线的焦点坐标在坐标轴上确定,而不知道开口方向时,可以设抛物线的方程为y2=ax(a≠0)(焦点在x轴上)或x2=ay(a≠0)(焦点在y轴上).
基础小测
1.已知抛物线x2=4y上一点A的纵坐标为4,则点A到抛物线焦点的距离为( )
A. B.4
C.5 D.
2.经过点P(4,-2)的抛物线的标准方程为_____________________.
基础点二 抛物线的简单几何性质
标准 方程 y2=2px (p>0) y2=-2px (p>0) x2=2py (p>0) x2=-2py (p>0)
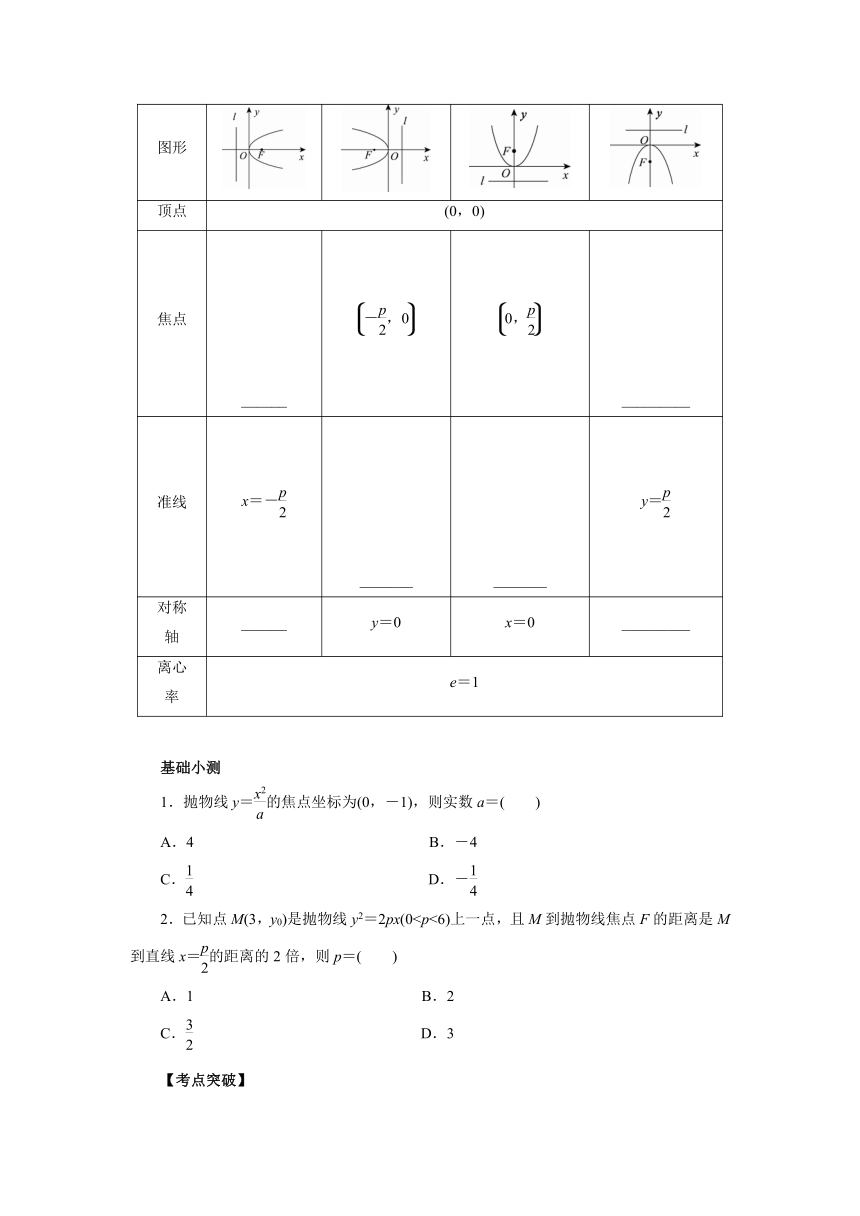
图形
顶点 (0,0)
焦点 ______ _________
准线 x=- _______ _______ y=
对称 轴 ______ y=0 x=0 _________
离心 率 e=1
基础小测
1.抛物线y=的焦点坐标为(0,-1),则实数a=( )
A.4 B.-4
C. D.-
2.已知点M(3,y0)是抛物线y2=2px(0A.1 B.2
C. D.3
【考点突破】
考点一 抛物线的定义的应用(高考热度:★★★)
[例1] 若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是________.
技法点拨:注意灵活运用抛物线上一点P(x0,y0)到焦点F的距离|PF|=|x0|+或|PF|=|y0|+.
同源变式
变式1将本典例条件变为“在抛物线上找一点M,使|MA|+|MF|最小,其中A(3,2) ”,则点M的坐标为________,此时的最小值为________.
变式2 将本典例条件变为“在抛物线上有一动点M到y轴的距离为d1,到直线l:x-y+5=0的距离为d2”,则d1+d2的最小值为________.
归纳点拨
利用抛物线的定义可解决的两类问题
(1)轨迹问题:用抛物线的定义可以确定动点与定点、定直线距离有关的轨迹是不是抛物线.
(2)距离问题:该类问题一般情况下与抛物线的定义有关,实现由点到点的距离与点到直线的距离的相互转化.
①将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”,使问题得解.
②将抛物线上的点到焦点的距离转化为到准线的距离,利用与直线上所有点的连线中“垂线段最短”原理解决.
考点微练
1.(2020届福建南安侨光中学高三月考)F是抛物线y2=2x的焦点,A,B是抛物线上的两点,|AF|+|BF|=8,则线段AB的中点到y轴的距离为( )
A.4 B.
C.3 D.
2.(多选题)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若∠ABD=90°,且△ABF的面积为9,则( )
A.△ABF是等边三角形
B.|BF|=3
C.点F到准线的距离为3
D.抛物线C的方程为y2=6x
3.(2020届山东模拟)直线l过抛物线C:y2=2px(p>0)的焦点F(1,0),且与C交于A,B两点,则p=________,+=________.
考点二 抛物线的标准方程与几何性质(高考热度:★★)
[例2] (全国卷Ⅱ)若抛物线y2=2px(p>0)的焦点是椭圆+=1的一个焦点,则p=( )
A.2 B.3
C.4 D.8
[例3] (武汉调研)如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于点C,若|BC|=2|BF|,且|AF|=6,则此抛物线方程为( )
A.y2=9x B.y2=6x
C.y2=3x D.y2=x
解题技法
1.求抛物线标准方程的方法
(1)定义法:若题目已给出抛物线的方程(含有未知数p),那么只需求出p即可.
(2)待定系数法:若题目未给出抛物线的方程,对于焦点在x轴上的抛物线的标准方程可统一设为y2=ax(a≠0),a的正负由题设来定;焦点在y轴上的抛物线的标准方程可设为x2=ay(a≠0),这样就减少了不必要的讨论.
2.抛物线性质的应用技巧
(1)利用抛物线方程确定及应用其焦点、准线时,关键是将抛物线方程化成标准方程.
(2)要结合图形分析,灵活运用平面图形的性质简化运算.
考点微练
1.设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且与y轴交于点A.若△OAF(O为坐标原点)的面积为4,则抛物线的方程为( )
A.y2=±4x B.y2=±8x
C.y2=4x D.y2=8x
2.已知抛物线C的顶点为原点,焦点在x轴上,直线y=x与抛物线C交于A,B两点,若P(2,2)为AB的中点,则抛物线C的方程为________.
3.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线-=1相交于A,B两点,若△ABF为等边三角形,则p=________,抛物线的焦点到双曲线渐近线的距离为________.
参考答案
【基础梳理】
基础点一 抛物线的定义与标准方程
基础小测
1.解析:因为抛物线x2=4y的准线方程为y=-1,所以点A到准线的距离为5.根据抛物线定义可知点A到焦点的距离为5.故选C.
2.解析:由点P在第四象限,则抛物线的开口方向为向右或向下,所以可设该抛物线的方程为y2=2px或x2=-2py(p>0),将点P的坐标分别代入两方程得,所求抛物线的方程为y2=x或x2=-8y.
基础点二 抛物线的简单几何性质
基础小测
1.解析:抛物线y=的标准方程为 x2= ay,焦点坐标为 .由题意可知=-1,解得a=-4.故选B.
2.解析:|MF|=x0+=3+,即3+=2×,解得p=2或p=18(舍).故选B.
【考点突破】
考点一 抛物线的定义的应用(高考热度:★★★)
[例1] 解析:设M(x0,y0).由抛物线方程知焦点F(1,0).根据抛物线的定义得|MF|=x0+1=10,∴x0=9,即点M到y轴的距离为9.
同源变式
变式1 解析:如图,点A在抛物线y2=4x的内部,由抛物线的定义可知,|MA|+|MF|=|MA|+|MH|,
其中|MH|为点M到抛物线的准线的距离.
过A作抛物线准线的垂线交抛物线于M1,垂足为B,则|MA|+|MF|=|MA|+|MH|≥|AB|=4,当且仅当点M在M1的位置时等号成立.此时点M1的坐标为(1,2).
变式2 解析:由题意知,抛物线的焦点为F(1,0).点M到y轴的距离d1=|MF|-1,所以d1+d2=d2+|MF|-1.易知d2+|MF|的最小值为点F到直线l的距离,故d2+|MF|的最小值为=3,所以d1+d2的最小值为3-1.
考点微练
1.解析:∵F是抛物线y2=2x的焦点,
∴F,准线方程为x=-. 设A(x1,y1),B(x2,y2),
∴|AF|+|BF|=x1++x2+=8,
∴x1+x2=7,∴线段AB的中点的横坐标为,
∴线段AB的中点到y轴的距离为.
2.解析:∵以F为圆心,|FA|为半径的圆交l于B,D两点,∠ABD=90°,由抛物线的定义可得|AB|=|AF|=|BF|,∴△ABF是等边三角形,∴∠FBD=30°.∵△ABF的面积为|BF|2=9,∴|BF|=6.又点F到准线的距离为|BF|sin 30°=3=p,则该抛物线的方程为y2=6x.
3.解析:由抛物线y2=2px的焦点为F(1,0),得=1,∴p=2.又∵F是抛物线的焦点,根据焦点弦的性质得+==1.
考点二 抛物线的标准方程与几何性质(高考热度:★★)
[例2] 答案:D
解析:∵抛物线y2=2px(p>0)的焦点坐标为,
∴由已知得椭圆+=1的一个焦点为,
∴3p-p=,又p>0,∴p=8.
[例3] 答案:B
解析:如图,分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,则由已知得:|BC|=2a,由抛物线定义得:|BD|=a,故∠BCD=30°,在直角三角形ACE中,因为|AE|=|AF|=6,|AC|=6+3a,2|AE|=|AC|,所以6+3a=12,从而得a=2,|FC|=3a=6,所以p=|FG|=|FC|=3,因此抛物线方程为y2=6x.
考点微练
1.解析:抛物线y2=ax(a≠0)的焦点F的坐标为,则直线l的方程为y=2,它与y轴的交点为A,所以△OAF的面积为·=4,解得a=±8,所以所求抛物线的方程为y2=±8x.故选B.
2.解析:设抛物线的方程为y2=ax(a≠0),与y=x联立,消去y,得x2-ax=0,xA+xB=a=2×2=4,故y2=4x.
3.解析:抛物线的焦点坐标为,准线方程为y=-,准线方程与双曲线方程联立可得-=1,解得x=±.因为△ABF为等边三角形,所以|AB|=p,即×2=p,解得p=6.则抛物线焦点坐标为(0,3),双曲线的渐近线方程为y=±x,则抛物线的焦点到双曲线渐近线的距离为=.
新课程标准 考向预测
1.了解抛物线的实际背景,感受抛物线在刻画现实世界和解决实际问题中的应用. 2.了解抛物线的定义、几何图形和标准方程,以及它的简单几何性质. 3.通过抛物线的学习,进一步体会数形结合的思想. 4.了解抛物线的简单应用. 命题角度 1.抛物线的定义及应用 2.抛物线的标准方程与几何性质 3.直线与抛物线的位置关系
核心素养 数学运算、运算推理、直观想象
【基础梳理】
基础点一 抛物线的定义与标准方程
1.抛物线的定义:平面内到一个定点F和一条定直线l(l不经过定点F)____________的点的轨迹是抛物线.定点F叫做抛物线的________,定直线l叫做抛物线的________.
2.抛物线的标准方程
(1)焦参数为p,焦点在x轴正半轴上的抛物线的标准方程是____________________;
(2)焦参数为p,焦点在x轴负半轴上的抛物线的标准方程是____________________;
(3)焦参数为p,焦点在y轴正半轴上的抛物线的标准方程是____________________;
(4)焦参数为p,焦点在y轴负半轴上的抛物线的标准方程是____________________.
焦参数p的几何意义:焦点F到准线l的距离.
必记结论:当抛物线的焦点坐标在坐标轴上确定,而不知道开口方向时,可以设抛物线的方程为y2=ax(a≠0)(焦点在x轴上)或x2=ay(a≠0)(焦点在y轴上).
基础小测
1.已知抛物线x2=4y上一点A的纵坐标为4,则点A到抛物线焦点的距离为( )
A. B.4
C.5 D.
2.经过点P(4,-2)的抛物线的标准方程为_____________________.
基础点二 抛物线的简单几何性质
标准 方程 y2=2px (p>0) y2=-2px (p>0) x2=2py (p>0) x2=-2py (p>0)
图形
顶点 (0,0)
焦点 ______ _________
准线 x=- _______ _______ y=
对称 轴 ______ y=0 x=0 _________
离心 率 e=1
基础小测
1.抛物线y=的焦点坐标为(0,-1),则实数a=( )
A.4 B.-4
C. D.-
2.已知点M(3,y0)是抛物线y2=2px(0
C. D.3
【考点突破】
考点一 抛物线的定义的应用(高考热度:★★★)
[例1] 若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是________.
技法点拨:注意灵活运用抛物线上一点P(x0,y0)到焦点F的距离|PF|=|x0|+或|PF|=|y0|+.
同源变式
变式1将本典例条件变为“在抛物线上找一点M,使|MA|+|MF|最小,其中A(3,2) ”,则点M的坐标为________,此时的最小值为________.
变式2 将本典例条件变为“在抛物线上有一动点M到y轴的距离为d1,到直线l:x-y+5=0的距离为d2”,则d1+d2的最小值为________.
归纳点拨
利用抛物线的定义可解决的两类问题
(1)轨迹问题:用抛物线的定义可以确定动点与定点、定直线距离有关的轨迹是不是抛物线.
(2)距离问题:该类问题一般情况下与抛物线的定义有关,实现由点到点的距离与点到直线的距离的相互转化.
①将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”,使问题得解.
②将抛物线上的点到焦点的距离转化为到准线的距离,利用与直线上所有点的连线中“垂线段最短”原理解决.
考点微练
1.(2020届福建南安侨光中学高三月考)F是抛物线y2=2x的焦点,A,B是抛物线上的两点,|AF|+|BF|=8,则线段AB的中点到y轴的距离为( )
A.4 B.
C.3 D.
2.(多选题)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若∠ABD=90°,且△ABF的面积为9,则( )
A.△ABF是等边三角形
B.|BF|=3
C.点F到准线的距离为3
D.抛物线C的方程为y2=6x
3.(2020届山东模拟)直线l过抛物线C:y2=2px(p>0)的焦点F(1,0),且与C交于A,B两点,则p=________,+=________.
考点二 抛物线的标准方程与几何性质(高考热度:★★)
[例2] (全国卷Ⅱ)若抛物线y2=2px(p>0)的焦点是椭圆+=1的一个焦点,则p=( )
A.2 B.3
C.4 D.8
[例3] (武汉调研)如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于点C,若|BC|=2|BF|,且|AF|=6,则此抛物线方程为( )
A.y2=9x B.y2=6x
C.y2=3x D.y2=x
解题技法
1.求抛物线标准方程的方法
(1)定义法:若题目已给出抛物线的方程(含有未知数p),那么只需求出p即可.
(2)待定系数法:若题目未给出抛物线的方程,对于焦点在x轴上的抛物线的标准方程可统一设为y2=ax(a≠0),a的正负由题设来定;焦点在y轴上的抛物线的标准方程可设为x2=ay(a≠0),这样就减少了不必要的讨论.
2.抛物线性质的应用技巧
(1)利用抛物线方程确定及应用其焦点、准线时,关键是将抛物线方程化成标准方程.
(2)要结合图形分析,灵活运用平面图形的性质简化运算.
考点微练
1.设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且与y轴交于点A.若△OAF(O为坐标原点)的面积为4,则抛物线的方程为( )
A.y2=±4x B.y2=±8x
C.y2=4x D.y2=8x
2.已知抛物线C的顶点为原点,焦点在x轴上,直线y=x与抛物线C交于A,B两点,若P(2,2)为AB的中点,则抛物线C的方程为________.
3.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线-=1相交于A,B两点,若△ABF为等边三角形,则p=________,抛物线的焦点到双曲线渐近线的距离为________.
参考答案
【基础梳理】
基础点一 抛物线的定义与标准方程
基础小测
1.解析:因为抛物线x2=4y的准线方程为y=-1,所以点A到准线的距离为5.根据抛物线定义可知点A到焦点的距离为5.故选C.
2.解析:由点P在第四象限,则抛物线的开口方向为向右或向下,所以可设该抛物线的方程为y2=2px或x2=-2py(p>0),将点P的坐标分别代入两方程得,所求抛物线的方程为y2=x或x2=-8y.
基础点二 抛物线的简单几何性质
基础小测
1.解析:抛物线y=的标准方程为 x2= ay,焦点坐标为 .由题意可知=-1,解得a=-4.故选B.
2.解析:|MF|=x0+=3+,即3+=2×,解得p=2或p=18(舍).故选B.
【考点突破】
考点一 抛物线的定义的应用(高考热度:★★★)
[例1] 解析:设M(x0,y0).由抛物线方程知焦点F(1,0).根据抛物线的定义得|MF|=x0+1=10,∴x0=9,即点M到y轴的距离为9.
同源变式
变式1 解析:如图,点A在抛物线y2=4x的内部,由抛物线的定义可知,|MA|+|MF|=|MA|+|MH|,
其中|MH|为点M到抛物线的准线的距离.
过A作抛物线准线的垂线交抛物线于M1,垂足为B,则|MA|+|MF|=|MA|+|MH|≥|AB|=4,当且仅当点M在M1的位置时等号成立.此时点M1的坐标为(1,2).
变式2 解析:由题意知,抛物线的焦点为F(1,0).点M到y轴的距离d1=|MF|-1,所以d1+d2=d2+|MF|-1.易知d2+|MF|的最小值为点F到直线l的距离,故d2+|MF|的最小值为=3,所以d1+d2的最小值为3-1.
考点微练
1.解析:∵F是抛物线y2=2x的焦点,
∴F,准线方程为x=-. 设A(x1,y1),B(x2,y2),
∴|AF|+|BF|=x1++x2+=8,
∴x1+x2=7,∴线段AB的中点的横坐标为,
∴线段AB的中点到y轴的距离为.
2.解析:∵以F为圆心,|FA|为半径的圆交l于B,D两点,∠ABD=90°,由抛物线的定义可得|AB|=|AF|=|BF|,∴△ABF是等边三角形,∴∠FBD=30°.∵△ABF的面积为|BF|2=9,∴|BF|=6.又点F到准线的距离为|BF|sin 30°=3=p,则该抛物线的方程为y2=6x.
3.解析:由抛物线y2=2px的焦点为F(1,0),得=1,∴p=2.又∵F是抛物线的焦点,根据焦点弦的性质得+==1.
考点二 抛物线的标准方程与几何性质(高考热度:★★)
[例2] 答案:D
解析:∵抛物线y2=2px(p>0)的焦点坐标为,
∴由已知得椭圆+=1的一个焦点为,
∴3p-p=,又p>0,∴p=8.
[例3] 答案:B
解析:如图,分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,则由已知得:|BC|=2a,由抛物线定义得:|BD|=a,故∠BCD=30°,在直角三角形ACE中,因为|AE|=|AF|=6,|AC|=6+3a,2|AE|=|AC|,所以6+3a=12,从而得a=2,|FC|=3a=6,所以p=|FG|=|FC|=3,因此抛物线方程为y2=6x.
考点微练
1.解析:抛物线y2=ax(a≠0)的焦点F的坐标为,则直线l的方程为y=2,它与y轴的交点为A,所以△OAF的面积为·=4,解得a=±8,所以所求抛物线的方程为y2=±8x.故选B.
2.解析:设抛物线的方程为y2=ax(a≠0),与y=x联立,消去y,得x2-ax=0,xA+xB=a=2×2=4,故y2=4x.
3.解析:抛物线的焦点坐标为,准线方程为y=-,准线方程与双曲线方程联立可得-=1,解得x=±.因为△ABF为等边三角形,所以|AB|=p,即×2=p,解得p=6.则抛物线焦点坐标为(0,3),双曲线的渐近线方程为y=±x,则抛物线的焦点到双曲线渐近线的距离为=.
