第五单元 第10课时 用方程解决问题(5)(课件)五年级数学上册 最新人教版(共19张PPT)
文档属性
| 名称 | 第五单元 第10课时 用方程解决问题(5)(课件)五年级数学上册 最新人教版(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-13 10:20:13 | ||
图片预览





文档简介
(共19张PPT)
简易方程
人教版五年级数学上册
第10课时 ɑx±bx=c的应用
5
1.一辆汽车平均每小时行驶60千米,x小时共行驶( )千米。
2.小明骑自行车每分钟能行x米,那么15分钟能行( )米。
3.甲车每小时行40千米,乙车每小时行52千米,两辆车各行驶了x小时,两车共行驶了( )千米。
60x
15x
40x+52x
(教材第79页例5)
从图中你获取了哪些条件?
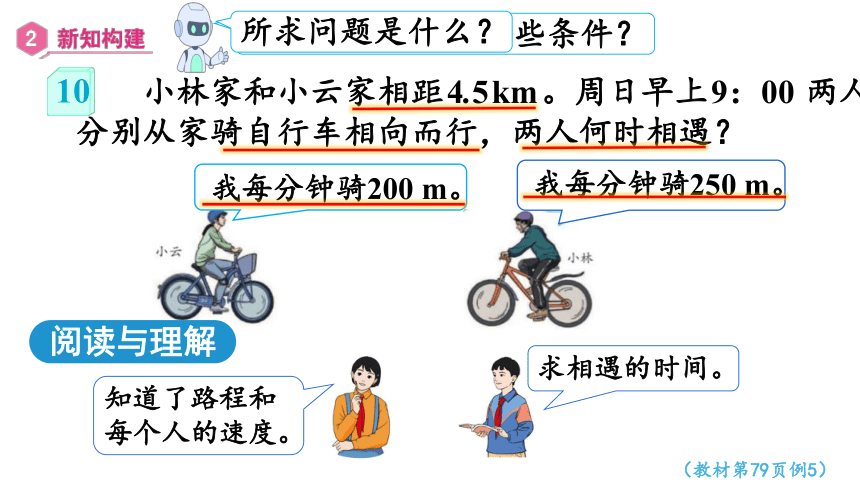
小林家和小云家相距4.5km。周日早上9:00 两人分别从家骑自行车相向而行,两人何时相遇?
阅读与理解
求相遇的时间。
知道了路程和每个人的速度。
10
我每分钟骑200 m。
我每分钟骑250 m。
所求问题是什么?
4.5km
相遇
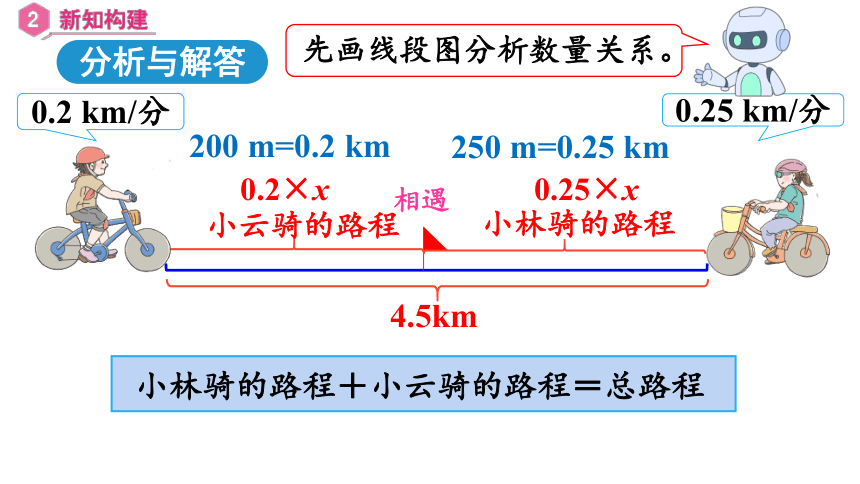
小云骑的路程
小林骑的路程
0.2 km/分
0.25 km/分
200 m=0.2 km
250 m=0.25 km
小林骑的路程+小云骑的路程=总路程
分析与解答
先画线段图分析数量关系。
0.2×x
0.25×x
0.25x+0.2x = 4.5
0.45x = 4.5
0.45x÷0.45 = 4.5÷0.45
x = 10
解:设两人 x 分钟后相遇。
答:两人9:10可以相遇。
小林骑的路程+小云骑的路程=总路程
分析与解答
还可以怎样列方程?
9:00过10分钟就是9:10。
小林的路程+小云的路程
=0.25×10+0.2×10
=4.5
=总路程
(0.25+0.2)x = 4.5
0.45x = 4.5
0.45x÷0.45 = 4.5÷0.45
x = 10
解:设两人 x 分钟后相遇。
答:两人9:10可以相遇。
两人每分钟骑的路程和×时间=总路程
分析与解答
两人每分钟的路程和×小云的路程
=(0.25+0.2)×10
=4.5
=总路程
9:00过10分钟就是9:10。
解:设两人x分钟后相遇。
0.25x+0.2x=4.5
0.45x=4.5
x=10
答:两人9:10相遇。
解:设两人x分钟后相遇。
(0.25+0.2)x=4.5
0.45x=4.5
x=10
答:两人在9:10相遇。
比较这两种解法,有什么相同的地方?
通过画线段图可以清楚地分析数量之间的相等关系。
这里要用到速度、时间和路程的数量关系来列方程。
回顾与反思
1.相遇问题的基本特征:两个物体同时由两地出发,相向而行,在途中相遇。
2.相遇问题的基本关系:
甲行的路程+乙行的路程=总路程
或甲乙速度和×相遇时间=总路程
速度和×相遇时间=总路程__________________
1.甲、乙两地相距380 km,客车与货车同时从两地相对开出,4小时后在途中相遇。已知客车每小时行 45 km,货车每小时行x km。
(1)连一连。
速度和是多少? 45×4
相遇时客车行了多少千米? 4x
相遇时货车行了多少千米? 45+x
(2)
(x+45)×4=380
(3)甲车行的路程+乙车行的路程=总路程____________________
45×4+4x=380
(教材第80页第9题)
解:设经过x小时两车相遇。
230x+170x = 600
400x = 600
400x÷400 = 600 ÷400
x = 1.5
2. 两列火车从相距600km的两地同时相向开出。甲车每小时行230km,乙车每小时行170km,经过几小时两车相遇?
甲火车行的路程+乙火车行的路程=总路程
路程
两车速度
相遇时间
答:经过1.5小时
两车相遇。
3. 两地间的路程是455km,甲、乙两辆汽车同时从两地开出,相向而行,经过3.5小时相遇。甲车每小时行68km,乙车每小时行多少千米?
解:设乙车每小时行x千米。
68×3.5+3.5x = 455
238+3.5x = 455
3.5x = 217
x = 62
答:乙车每小时行62千米。
(教材第80页第10题)
甲车行的路程+乙车行的路程=总路程
时间
路程
还可以怎样列方程?
甲乙两车的速度和×相遇时间=总路程
解:设乙车每小时行x千米。
(68+x)×3.5 = 455
(68+x)×3.5 ÷3.5 = 455 ÷3.5
68+x = 130
68+x-68 = 130-68
x = 62
答:乙车每小时行62千米。
3. 两地间的路程是455km,甲、乙两辆汽车同时从两地开出,相向而行,经过3.5小时相遇。甲车每小时行68km,乙车每小时行多少千米?
(教材第82页第14题)
4. 甲、乙两艘轮船同时从上海出发开往青岛。经过18小时后,甲船落后乙船57.6km。甲船每小时行32.5km,乙船每小时行多少千米
57.6km
甲18小时行
乙18小时行
57.6km
上海
青岛
甲
乙
乙船行的路程-甲船行的路程=落后的距离
解:设乙船每小时行x km。
18x-18×32.5=57.6
x=35.7
答:乙船每小时行35.7km。
假设没有这75km,甲乙两车就相遇了。
5. 两地相距350km,甲、乙两车同时从两地出发相向而行。甲车每小时行50km,出发2.5小时后两车还差75km相遇,乙车每小时行多少千米
甲车50km/时
乙车x km/时
350km
75km
甲车路程+乙车路程=总路程-相差距离
解:设乙车每小时行x km。
50×2.5+2.5x = 350-75
125+2.5x = 275
125+2.5x-125 = 275-125
2.5x = 150
2.5x÷2.5 = 150÷2.5
x = 60
甲车路程+乙车路程=总路程-相差距离
答:乙船每小时行60km。
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,乒乓球没有了,羽毛球还剩6个。一共取了几次,原来乒乓球和羽毛球各有多少个
6.
要求一共取了几次,也就是求乒乓球、羽毛球都各取了几次。
(教材第82页思考题)
根据两种球数量相等或取了x次后,乒乓球没了,羽毛球还剩6个可以列出不同的方程。
设一共取了x次,则原来乒乓球有5x个,羽毛球(3x+6)个。
乒乓球个数=羽毛球个数
解:一共取了x 次。
5x = 3x+6
5x-3x = 3x+6-3x
2x = 6
x = 3
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,乒乓球没有了,羽毛球还剩6个。一共取了几次,原来乒乓球和羽毛球各有多少个
6.
方法一
原来乒乓球:5×3=15(个)
羽毛球:3×3+6=15(个)
答:一共取了3次,原来乒
乓球和羽毛球各15个。
解:一共取了x 次。
5x-3x = 6
2x = 6
x = 3
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,乒乓球没有了,羽毛球还剩6个。一共取了几次,原来乒乓球和羽毛球各有多少个
6.
方法二
原来乒乓球:5×3=15(个)
羽毛球:3×3+6=15(个)
答:一共取了3次,原来乒
乓球和羽毛球各15个。
取出的乒乓球个数-取出的羽毛球个数=6
这节课你有什么收获?
解答行程问题的步骤
1.画线段图分析数量关系,找出等量关系;
2.根据速度、时间和路程三者之间的数量关系列方程
解答。
简易方程
人教版五年级数学上册
第10课时 ɑx±bx=c的应用
5
1.一辆汽车平均每小时行驶60千米,x小时共行驶( )千米。
2.小明骑自行车每分钟能行x米,那么15分钟能行( )米。
3.甲车每小时行40千米,乙车每小时行52千米,两辆车各行驶了x小时,两车共行驶了( )千米。
60x
15x
40x+52x
(教材第79页例5)
从图中你获取了哪些条件?
小林家和小云家相距4.5km。周日早上9:00 两人分别从家骑自行车相向而行,两人何时相遇?
阅读与理解
求相遇的时间。
知道了路程和每个人的速度。
10
我每分钟骑200 m。
我每分钟骑250 m。
所求问题是什么?
4.5km
相遇
小云骑的路程
小林骑的路程
0.2 km/分
0.25 km/分
200 m=0.2 km
250 m=0.25 km
小林骑的路程+小云骑的路程=总路程
分析与解答
先画线段图分析数量关系。
0.2×x
0.25×x
0.25x+0.2x = 4.5
0.45x = 4.5
0.45x÷0.45 = 4.5÷0.45
x = 10
解:设两人 x 分钟后相遇。
答:两人9:10可以相遇。
小林骑的路程+小云骑的路程=总路程
分析与解答
还可以怎样列方程?
9:00过10分钟就是9:10。
小林的路程+小云的路程
=0.25×10+0.2×10
=4.5
=总路程
(0.25+0.2)x = 4.5
0.45x = 4.5
0.45x÷0.45 = 4.5÷0.45
x = 10
解:设两人 x 分钟后相遇。
答:两人9:10可以相遇。
两人每分钟骑的路程和×时间=总路程
分析与解答
两人每分钟的路程和×小云的路程
=(0.25+0.2)×10
=4.5
=总路程
9:00过10分钟就是9:10。
解:设两人x分钟后相遇。
0.25x+0.2x=4.5
0.45x=4.5
x=10
答:两人9:10相遇。
解:设两人x分钟后相遇。
(0.25+0.2)x=4.5
0.45x=4.5
x=10
答:两人在9:10相遇。
比较这两种解法,有什么相同的地方?
通过画线段图可以清楚地分析数量之间的相等关系。
这里要用到速度、时间和路程的数量关系来列方程。
回顾与反思
1.相遇问题的基本特征:两个物体同时由两地出发,相向而行,在途中相遇。
2.相遇问题的基本关系:
甲行的路程+乙行的路程=总路程
或甲乙速度和×相遇时间=总路程
速度和×相遇时间=总路程__________________
1.甲、乙两地相距380 km,客车与货车同时从两地相对开出,4小时后在途中相遇。已知客车每小时行 45 km,货车每小时行x km。
(1)连一连。
速度和是多少? 45×4
相遇时客车行了多少千米? 4x
相遇时货车行了多少千米? 45+x
(2)
(x+45)×4=380
(3)甲车行的路程+乙车行的路程=总路程____________________
45×4+4x=380
(教材第80页第9题)
解:设经过x小时两车相遇。
230x+170x = 600
400x = 600
400x÷400 = 600 ÷400
x = 1.5
2. 两列火车从相距600km的两地同时相向开出。甲车每小时行230km,乙车每小时行170km,经过几小时两车相遇?
甲火车行的路程+乙火车行的路程=总路程
路程
两车速度
相遇时间
答:经过1.5小时
两车相遇。
3. 两地间的路程是455km,甲、乙两辆汽车同时从两地开出,相向而行,经过3.5小时相遇。甲车每小时行68km,乙车每小时行多少千米?
解:设乙车每小时行x千米。
68×3.5+3.5x = 455
238+3.5x = 455
3.5x = 217
x = 62
答:乙车每小时行62千米。
(教材第80页第10题)
甲车行的路程+乙车行的路程=总路程
时间
路程
还可以怎样列方程?
甲乙两车的速度和×相遇时间=总路程
解:设乙车每小时行x千米。
(68+x)×3.5 = 455
(68+x)×3.5 ÷3.5 = 455 ÷3.5
68+x = 130
68+x-68 = 130-68
x = 62
答:乙车每小时行62千米。
3. 两地间的路程是455km,甲、乙两辆汽车同时从两地开出,相向而行,经过3.5小时相遇。甲车每小时行68km,乙车每小时行多少千米?
(教材第82页第14题)
4. 甲、乙两艘轮船同时从上海出发开往青岛。经过18小时后,甲船落后乙船57.6km。甲船每小时行32.5km,乙船每小时行多少千米
57.6km
甲18小时行
乙18小时行
57.6km
上海
青岛
甲
乙
乙船行的路程-甲船行的路程=落后的距离
解:设乙船每小时行x km。
18x-18×32.5=57.6
x=35.7
答:乙船每小时行35.7km。
假设没有这75km,甲乙两车就相遇了。
5. 两地相距350km,甲、乙两车同时从两地出发相向而行。甲车每小时行50km,出发2.5小时后两车还差75km相遇,乙车每小时行多少千米
甲车50km/时
乙车x km/时
350km
75km
甲车路程+乙车路程=总路程-相差距离
解:设乙车每小时行x km。
50×2.5+2.5x = 350-75
125+2.5x = 275
125+2.5x-125 = 275-125
2.5x = 150
2.5x÷2.5 = 150÷2.5
x = 60
甲车路程+乙车路程=总路程-相差距离
答:乙船每小时行60km。
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,乒乓球没有了,羽毛球还剩6个。一共取了几次,原来乒乓球和羽毛球各有多少个
6.
要求一共取了几次,也就是求乒乓球、羽毛球都各取了几次。
(教材第82页思考题)
根据两种球数量相等或取了x次后,乒乓球没了,羽毛球还剩6个可以列出不同的方程。
设一共取了x次,则原来乒乓球有5x个,羽毛球(3x+6)个。
乒乓球个数=羽毛球个数
解:一共取了x 次。
5x = 3x+6
5x-3x = 3x+6-3x
2x = 6
x = 3
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,乒乓球没有了,羽毛球还剩6个。一共取了几次,原来乒乓球和羽毛球各有多少个
6.
方法一
原来乒乓球:5×3=15(个)
羽毛球:3×3+6=15(个)
答:一共取了3次,原来乒
乓球和羽毛球各15个。
解:一共取了x 次。
5x-3x = 6
2x = 6
x = 3
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,乒乓球没有了,羽毛球还剩6个。一共取了几次,原来乒乓球和羽毛球各有多少个
6.
方法二
原来乒乓球:5×3=15(个)
羽毛球:3×3+6=15(个)
答:一共取了3次,原来乒
乓球和羽毛球各15个。
取出的乒乓球个数-取出的羽毛球个数=6
这节课你有什么收获?
解答行程问题的步骤
1.画线段图分析数量关系,找出等量关系;
2.根据速度、时间和路程三者之间的数量关系列方程
解答。
