九年级数学北师版下册1.1 第1课时 锐角的正切 优质课件(共28张PPT)
文档属性
| 名称 | 九年级数学北师版下册1.1 第1课时 锐角的正切 优质课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 901.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-13 09:13:16 | ||
图片预览





文档简介
(共28张PPT)
第一章 直角三角形的边角关系
1 锐角三角函数
第1课时 锐角的正切
学习目标
【学习目标】
1.经历探索直角三角形中某锐角确定后其对边与邻边的比值也随之确定的过程,理解正切的意义.
2.能够用表示直角三角形中两边的比,表示生活中物体的倾斜程度,并能够用正切进行简单的计算.
【学习重点】
理解锐角三角函数正切的意义,用正切表示倾斜程度以及坡度.
【学习难点】
在现实情境中理解正切的意义.
学习重难点
情景导入
旧知回顾:
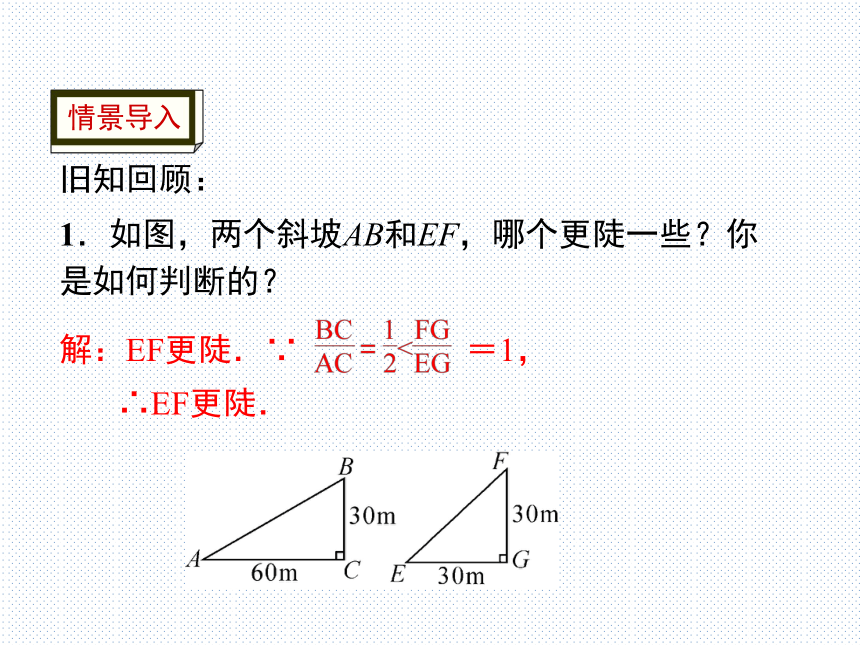
1.如图,两个斜坡AB和EF,哪个更陡一些?你是如何判断的?
解:EF更陡.∵ =1,
∴EF更陡.
情景导入
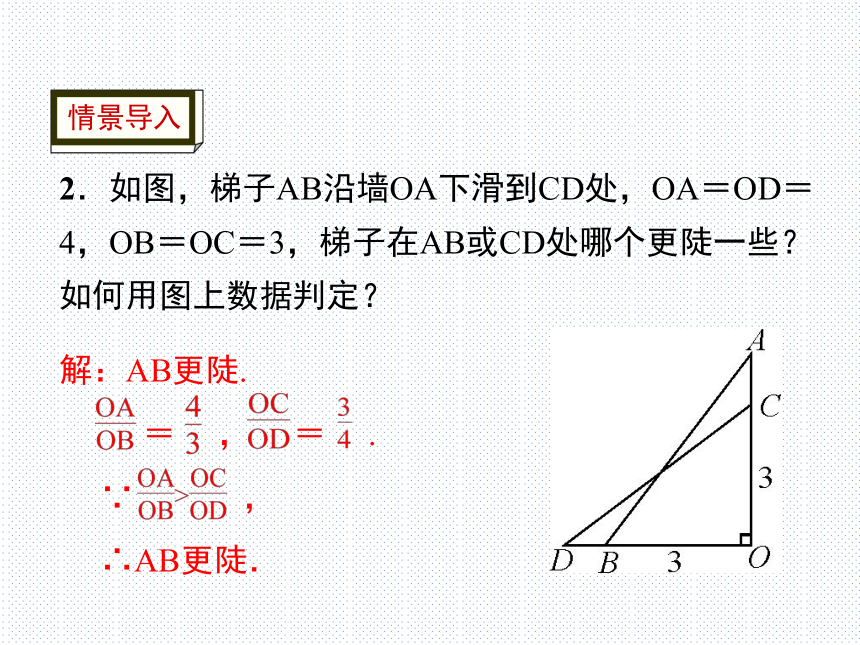
2.如图,梯子AB沿墙OA下滑到CD处,OA=OD=4,OB=OC=3,梯子在AB或CD处哪个更陡一些?如何用图上数据判定?
解:AB更陡.
= , = .
∵ ,
∴AB更陡.
知识模块一 正切的定义
自学互研
阅读教材P2~P3,完成下面的内容:
什么是锐角的正切?如何表示?
答:在直角三角形中,如果一个锐角确定,那么这个角的对边与邻边的比便随之确定.在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tan A,即tan A= .
生活中的梯子
自学互研
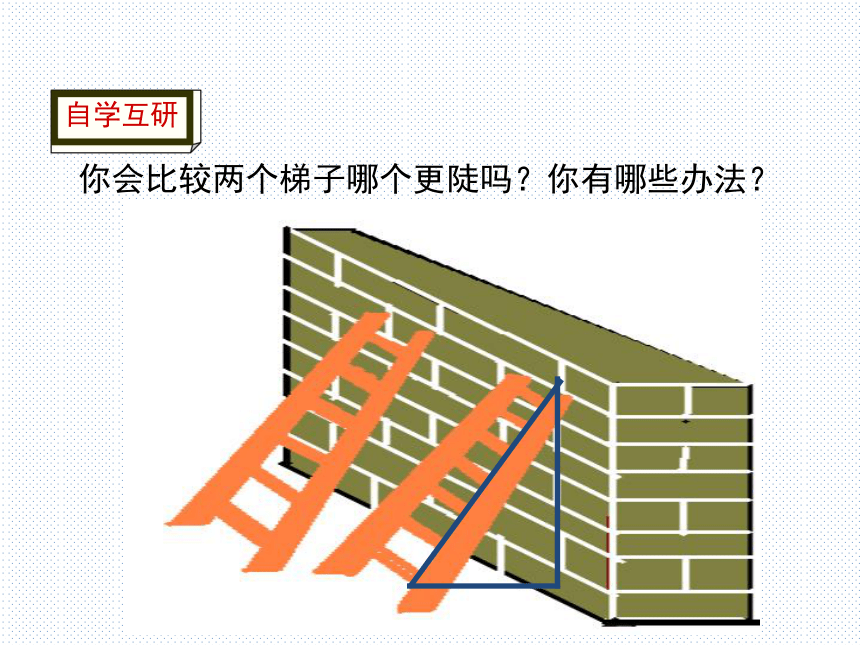
你会比较两个梯子哪个更陡吗?你有哪些办法?
自学互研
自学互研
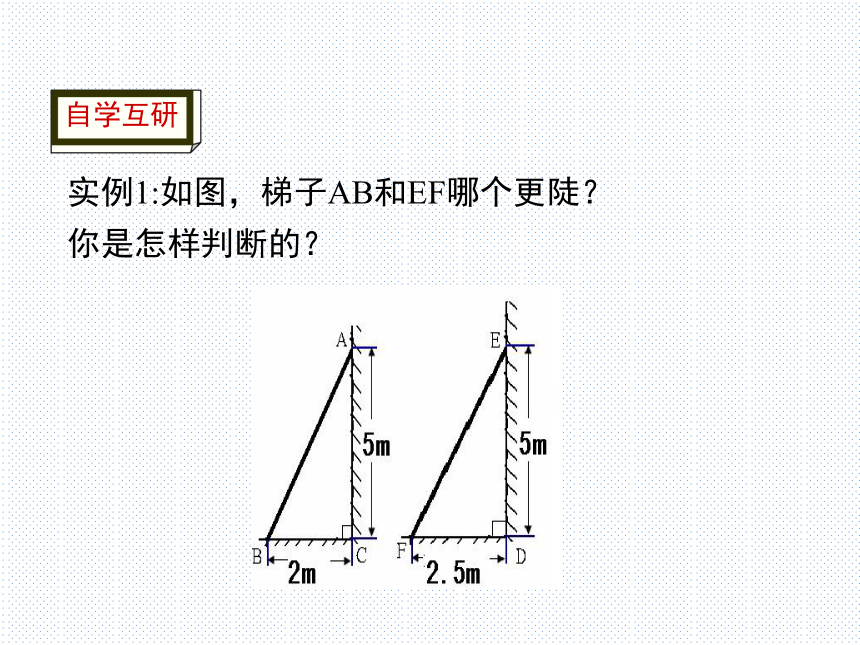
实例1:如图,梯子AB和EF哪个更陡?
你是怎样判断的?
实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?你能设法验证这个结论吗?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡。比值大的梯子陡。
4m
3.5m
1.5m
1.3m
自学互研
如图,小明想通过测量 及 ,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量 及 ,算出他们的比,也能说明梯子的倾斜程度,你同意小亮的看法吗?
生成问题
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
结论:tanA的值越大,梯子越陡.
归纳总结
(1) tanA是在直角三角形中定义的,
∠A是一 个锐角(注意构造直角三角形)。
(2)tanA是一个完整的符号,它表示∠A的正切记号里习惯省去角的符号“∠”。
注意:
(3) tanA是一个比值(直角边之比,注意比的顺序);且tanA﹥0,无单位。
(4) tanA的大小只与∠A的大小有关,而与直角三角形的大小无关。
在直角三角形中,若一个锐角确定,那么这个角对边与邻边的比值也是确定的。
归纳总结
自学互研
1:(广州中考)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=( )
A. B. C. D.
D
范例
自学互研
1:如图,在Rt△ABC中,CD是斜边AB上的高,BC=4,AC=3,设∠BCD=α,则tanα的值为( )
A. B. C. D.
B
仿例
自学互研
2:(烟台中考)如图,BD是菱形ABCD的对角线,CE⊥AB于点E,交BD于点F,且点E是AB的中点,则tan∠BFE的值是( )
A. B.2 C. D.
D
仿例
自学互研
3:在直角坐标系xOy中,点P(4,y)在第一象限内,且OP与x轴正半轴的夹角为60°,则y的值是( )
A. B.4 C.8 D.2
B
仿例
知识模块二 坡度
自学互研
阅读教材P3~P4,完成下面的内容:
什么是坡度?坡度与坡角的正切值有何关系?
答:坡面的铅直高度与水平宽度的比称为坡度或坡比.很显然坡度即坡角的正切值.坡角的正切值越大,坡度越陡.
怎样解答?
tanB的值越大,梯子越陡,∠B越大;
议一议
梯子的倾斜程度与tanB有什么关系?
2:如图为一水库大坝的横断面,坝高h=6m,迎水坡AB=10m,斜坡的坡度角为α,则迎水坡的坡度是______.
自学互研
范例
自学互研
1:如图,河堤横断面是梯形,上底为4m,堤高为6m,斜坡AD的坡比为1∶3,斜坡BC的坡角为45°,则河堤的横断面的面积为( )
A.96m2 B.48m2 C.192m2 D.84m2
A
仿例
自学互研
2:如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,若BC=6,AC=8,则tan∠ACD的值为______.
仿例
自学互研
3:如图,某人从山脚A走了300m的山路,爬到了120m高的小山顶B处,该山路的坡度为_____.
仿例
1、正切的定义。
2、梯子的倾斜程度与tanA的关系。 (∠A和tanA之间的关系)。
3、数形结合的方法;构造直角三角形的意识。
知识梳理
正切
定义
坡度
∠A越大,tanA越大,
梯子越陡
与梯子倾斜程度的关系
课堂小结
展示提升
知识模块一 正切的定义
知识模块二 坡度
检测反馈
【当堂检测】见所赠光盘和学生用书;
【课后检测】见学生用书.
第一章 直角三角形的边角关系
1 锐角三角函数
第1课时 锐角的正切
学习目标
【学习目标】
1.经历探索直角三角形中某锐角确定后其对边与邻边的比值也随之确定的过程,理解正切的意义.
2.能够用表示直角三角形中两边的比,表示生活中物体的倾斜程度,并能够用正切进行简单的计算.
【学习重点】
理解锐角三角函数正切的意义,用正切表示倾斜程度以及坡度.
【学习难点】
在现实情境中理解正切的意义.
学习重难点
情景导入
旧知回顾:
1.如图,两个斜坡AB和EF,哪个更陡一些?你是如何判断的?
解:EF更陡.∵ =1,
∴EF更陡.
情景导入
2.如图,梯子AB沿墙OA下滑到CD处,OA=OD=4,OB=OC=3,梯子在AB或CD处哪个更陡一些?如何用图上数据判定?
解:AB更陡.
= , = .
∵ ,
∴AB更陡.
知识模块一 正切的定义
自学互研
阅读教材P2~P3,完成下面的内容:
什么是锐角的正切?如何表示?
答:在直角三角形中,如果一个锐角确定,那么这个角的对边与邻边的比便随之确定.在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tan A,即tan A= .
生活中的梯子
自学互研
你会比较两个梯子哪个更陡吗?你有哪些办法?
自学互研
自学互研
实例1:如图,梯子AB和EF哪个更陡?
你是怎样判断的?
实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?你能设法验证这个结论吗?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡。比值大的梯子陡。
4m
3.5m
1.5m
1.3m
自学互研
如图,小明想通过测量 及 ,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量 及 ,算出他们的比,也能说明梯子的倾斜程度,你同意小亮的看法吗?
生成问题
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
结论:tanA的值越大,梯子越陡.
归纳总结
(1) tanA是在直角三角形中定义的,
∠A是一 个锐角(注意构造直角三角形)。
(2)tanA是一个完整的符号,它表示∠A的正切记号里习惯省去角的符号“∠”。
注意:
(3) tanA是一个比值(直角边之比,注意比的顺序);且tanA﹥0,无单位。
(4) tanA的大小只与∠A的大小有关,而与直角三角形的大小无关。
在直角三角形中,若一个锐角确定,那么这个角对边与邻边的比值也是确定的。
归纳总结
自学互研
1:(广州中考)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=( )
A. B. C. D.
D
范例
自学互研
1:如图,在Rt△ABC中,CD是斜边AB上的高,BC=4,AC=3,设∠BCD=α,则tanα的值为( )
A. B. C. D.
B
仿例
自学互研
2:(烟台中考)如图,BD是菱形ABCD的对角线,CE⊥AB于点E,交BD于点F,且点E是AB的中点,则tan∠BFE的值是( )
A. B.2 C. D.
D
仿例
自学互研
3:在直角坐标系xOy中,点P(4,y)在第一象限内,且OP与x轴正半轴的夹角为60°,则y的值是( )
A. B.4 C.8 D.2
B
仿例
知识模块二 坡度
自学互研
阅读教材P3~P4,完成下面的内容:
什么是坡度?坡度与坡角的正切值有何关系?
答:坡面的铅直高度与水平宽度的比称为坡度或坡比.很显然坡度即坡角的正切值.坡角的正切值越大,坡度越陡.
怎样解答?
tanB的值越大,梯子越陡,∠B越大;
议一议
梯子的倾斜程度与tanB有什么关系?
2:如图为一水库大坝的横断面,坝高h=6m,迎水坡AB=10m,斜坡的坡度角为α,则迎水坡的坡度是______.
自学互研
范例
自学互研
1:如图,河堤横断面是梯形,上底为4m,堤高为6m,斜坡AD的坡比为1∶3,斜坡BC的坡角为45°,则河堤的横断面的面积为( )
A.96m2 B.48m2 C.192m2 D.84m2
A
仿例
自学互研
2:如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,若BC=6,AC=8,则tan∠ACD的值为______.
仿例
自学互研
3:如图,某人从山脚A走了300m的山路,爬到了120m高的小山顶B处,该山路的坡度为_____.
仿例
1、正切的定义。
2、梯子的倾斜程度与tanA的关系。 (∠A和tanA之间的关系)。
3、数形结合的方法;构造直角三角形的意识。
知识梳理
正切
定义
坡度
∠A越大,tanA越大,
梯子越陡
与梯子倾斜程度的关系
课堂小结
展示提升
知识模块一 正切的定义
知识模块二 坡度
检测反馈
【当堂检测】见所赠光盘和学生用书;
【课后检测】见学生用书.
