人教版八年级数学上册与11.2三角形有关的角 导学练(附答案)
文档属性
| 名称 | 人教版八年级数学上册与11.2三角形有关的角 导学练(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 130.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-13 16:02:38 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版八年级数学上册与三角形有关的角导学练(附答案)
一、单选题
1.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,则∠DAC的度数为( )
A. 80° B. 82° C. 84° D. 86°
2.在△ABC中,∠A+∠B+∠C的度数为( )
A. 90° B. 180° C. 360° D. 不确定
3.如图, 中, , , ,则 等于( )
A. B. C. D.
4.如果在 中, ,则 等于( )
A. B. C. D.
5.如图,点E是 边 上的一点,点D在 的延长线上,连接 ,已知 ,则 ( )
A. B. C. D.
6.如图,∠B=∠C,则∠ADC与∠AEB的大小关系是( )
A. ∠ADC>∠AEB B. ∠ADC<∠AEB C. ∠ADC=∠AEB D. 大小关系不确定
7.在△ABC中,∠A-∠C=∠B,那么△ABC是( )
A. 等边三角形 B. 锐角三角形 C. 钝角三角形 D. 直角三角形
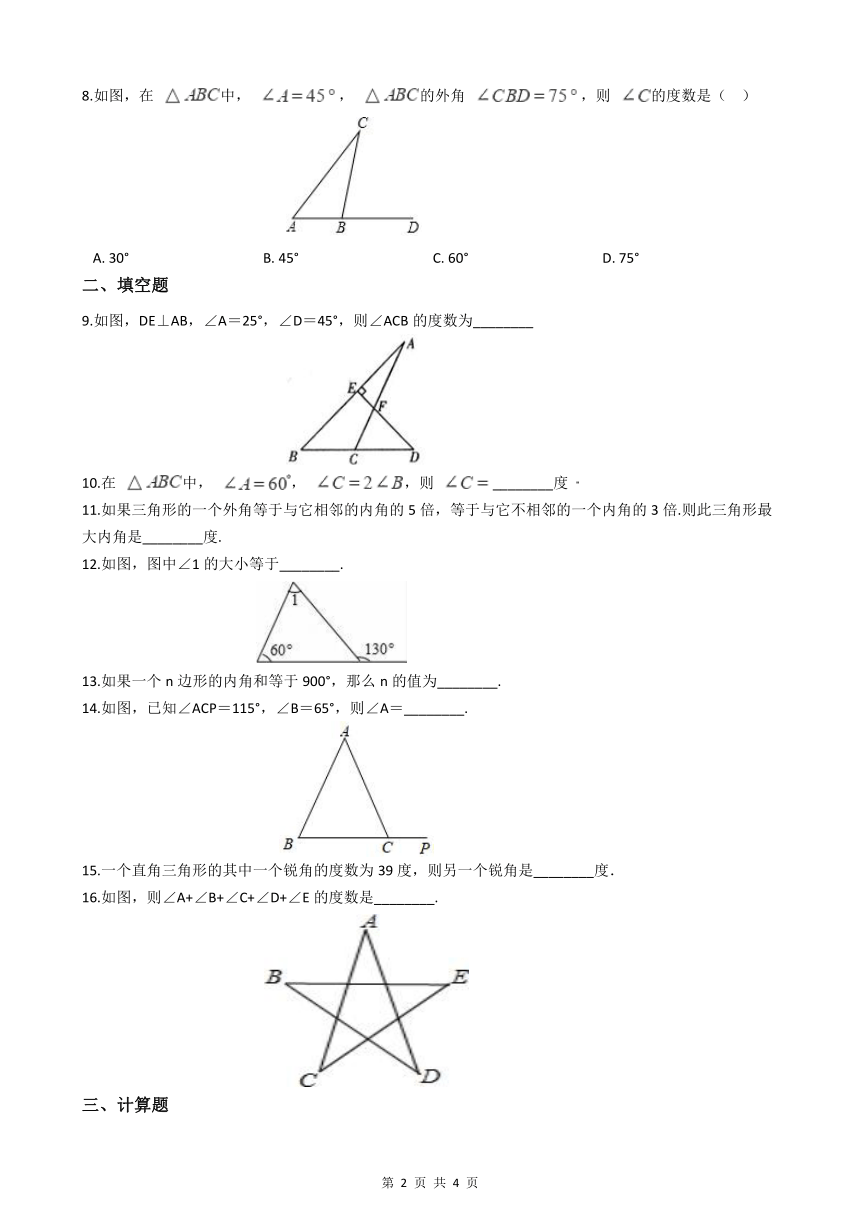
8.如图,在 中, , 的外角 ,则 的度数是( )
A. 30° B. 45° C. 60° D. 75°
二、填空题
9.如图,DE⊥AB,∠A=25°,∠D=45°,则∠ACB的度数为________
10.在 中, , ,则 ________度
11.如果三角形的一个外角等于与它相邻的内角的5倍,等于与它不相邻的一个内角的3倍.则此三角形最大内角是________度.
12.如图,图中∠1的大小等于________.
13.如果一个n边形的内角和等于900°,那么n的值为________.
14.如图,已知∠ACP=115°,∠B=65°,则∠A=________.
15.一个直角三角形的其中一个锐角的度数为39度,则另一个锐角是________度.
16.如图,则∠A+∠B+∠C+∠D+∠E的度数是________.
三、计算题
17.如图,在△ABC中,∠A=62°,∠1=20°,∠2=35°.求∠BDC的度数.
18.如图,在△ABC中,AE是∠BAC的角平分线,AD是BC边上的高,且∠B=44°,∠C=68°,求∠CAD、∠EAD的度数.
四、综合题
19.将一块直角三角板XYZ放置在AABC上,使得该三角板的两条直角边XY,XZ恰好分别经过点B,C.
(1)如图1,当∠A=45°时,∠ABC+∠ACB=________度,∠ABX+∠ACX=________度.
(2)如图2,改变直角三角板XYZ的位置,使该三角板的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否发生变化?若变化,请举例说明,若没有变化,请探究∠ABX+∠ACX与∠A的关系.
20.如图,根据要求作答
(1)如图1,AD平分∠BAC,AE⊥BC,∠B=30°,∠C=70°.
①∠BAC=________°,∠DAE=________°;
②如图2.若把“AE⊥BC”变成“点F在AD的延长线上,FE⊥BC”,其它条件不变,∠DFE的度数为________;
(2)如图3,AD平分∠BAC,AE平分∠BEC,∠C﹣∠B=40°,求∠DAE的度数.
答 案
一、单选题
1. A 2. B 3. B 4. C 5. A 6. C 7. D 8. A
二、填空题
9. 110° 10. 80 11. 100 12. 70° 13. 7 14. 50° 15. 51 16. 180°
三、计算题
17. 解:∵在△ABC中,∠A=62°, ∴∠ABC+∠ACB=180°﹣62°=118°.
∵∠1=20°,∠2=35°,
∴∠DBC+∠DCB=∠ABC+∠ACB﹣∠1﹣∠2=118°﹣20°﹣35°=63°.
∴∠BDC=180°﹣(∠DBC+∠DCB)=180°﹣63°=117°.
18. 解:∵在△ABC中,∠B=44°,∠C=68°,
∴∠BAC=180°﹣44°﹣68°=68°.
∵AE是∠BAC的角平分线,∴∠CAE= ∠BAC= ×68°=34°.
∵AD是BC边上的高,
∴∠ADC=90°,∴∠CAD=90°﹣∠C=90°﹣68°=22°,
∴∠EAD=∠CAE﹣∠CAD=34°﹣22°=12°.
四、综合题
19. (1)135;45
(2)解:不变化,∠ABX+∠ACX =90°-∠A,理由如下
∵∠x =90°,∴∠XBC+∠XCB =90°
∵∠A+∠ABC+∠ACB =180°,
∴∠ABX+∠ACX =(∠ABC-∠XBC)+(∠ACB-∠XCB)
=(∠ABC+∠ACB)-(∠XBC+∠XCB)=180°-∠A-90°=90°-∠A
20. (1)80;20;20°
(2)解:如图3,∵AD平分∠ABC,
∴∠BAD=∠CAD,
∵AE平分∠BEC,
∴∠AEB=∠AEC,
∵∠C+∠CAE+∠AEC=180°,∠B+∠BAE+∠AEB=180°,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD﹣∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD﹣∠DAE=∠B+∠BAD+∠DAE,
∴2∠DAE=∠C﹣∠B=40°,
∴∠DAE=20°.
(
第
- 1 -
页 共
5
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版八年级数学上册与三角形有关的角导学练(附答案)
一、单选题
1.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,则∠DAC的度数为( )
A. 80° B. 82° C. 84° D. 86°
2.在△ABC中,∠A+∠B+∠C的度数为( )
A. 90° B. 180° C. 360° D. 不确定
3.如图, 中, , , ,则 等于( )
A. B. C. D.
4.如果在 中, ,则 等于( )
A. B. C. D.
5.如图,点E是 边 上的一点,点D在 的延长线上,连接 ,已知 ,则 ( )
A. B. C. D.
6.如图,∠B=∠C,则∠ADC与∠AEB的大小关系是( )
A. ∠ADC>∠AEB B. ∠ADC<∠AEB C. ∠ADC=∠AEB D. 大小关系不确定
7.在△ABC中,∠A-∠C=∠B,那么△ABC是( )
A. 等边三角形 B. 锐角三角形 C. 钝角三角形 D. 直角三角形
8.如图,在 中, , 的外角 ,则 的度数是( )
A. 30° B. 45° C. 60° D. 75°
二、填空题
9.如图,DE⊥AB,∠A=25°,∠D=45°,则∠ACB的度数为________
10.在 中, , ,则 ________度
11.如果三角形的一个外角等于与它相邻的内角的5倍,等于与它不相邻的一个内角的3倍.则此三角形最大内角是________度.
12.如图,图中∠1的大小等于________.
13.如果一个n边形的内角和等于900°,那么n的值为________.
14.如图,已知∠ACP=115°,∠B=65°,则∠A=________.
15.一个直角三角形的其中一个锐角的度数为39度,则另一个锐角是________度.
16.如图,则∠A+∠B+∠C+∠D+∠E的度数是________.
三、计算题
17.如图,在△ABC中,∠A=62°,∠1=20°,∠2=35°.求∠BDC的度数.
18.如图,在△ABC中,AE是∠BAC的角平分线,AD是BC边上的高,且∠B=44°,∠C=68°,求∠CAD、∠EAD的度数.
四、综合题
19.将一块直角三角板XYZ放置在AABC上,使得该三角板的两条直角边XY,XZ恰好分别经过点B,C.
(1)如图1,当∠A=45°时,∠ABC+∠ACB=________度,∠ABX+∠ACX=________度.
(2)如图2,改变直角三角板XYZ的位置,使该三角板的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否发生变化?若变化,请举例说明,若没有变化,请探究∠ABX+∠ACX与∠A的关系.
20.如图,根据要求作答
(1)如图1,AD平分∠BAC,AE⊥BC,∠B=30°,∠C=70°.
①∠BAC=________°,∠DAE=________°;
②如图2.若把“AE⊥BC”变成“点F在AD的延长线上,FE⊥BC”,其它条件不变,∠DFE的度数为________;
(2)如图3,AD平分∠BAC,AE平分∠BEC,∠C﹣∠B=40°,求∠DAE的度数.
答 案
一、单选题
1. A 2. B 3. B 4. C 5. A 6. C 7. D 8. A
二、填空题
9. 110° 10. 80 11. 100 12. 70° 13. 7 14. 50° 15. 51 16. 180°
三、计算题
17. 解:∵在△ABC中,∠A=62°, ∴∠ABC+∠ACB=180°﹣62°=118°.
∵∠1=20°,∠2=35°,
∴∠DBC+∠DCB=∠ABC+∠ACB﹣∠1﹣∠2=118°﹣20°﹣35°=63°.
∴∠BDC=180°﹣(∠DBC+∠DCB)=180°﹣63°=117°.
18. 解:∵在△ABC中,∠B=44°,∠C=68°,
∴∠BAC=180°﹣44°﹣68°=68°.
∵AE是∠BAC的角平分线,∴∠CAE= ∠BAC= ×68°=34°.
∵AD是BC边上的高,
∴∠ADC=90°,∴∠CAD=90°﹣∠C=90°﹣68°=22°,
∴∠EAD=∠CAE﹣∠CAD=34°﹣22°=12°.
四、综合题
19. (1)135;45
(2)解:不变化,∠ABX+∠ACX =90°-∠A,理由如下
∵∠x =90°,∴∠XBC+∠XCB =90°
∵∠A+∠ABC+∠ACB =180°,
∴∠ABX+∠ACX =(∠ABC-∠XBC)+(∠ACB-∠XCB)
=(∠ABC+∠ACB)-(∠XBC+∠XCB)=180°-∠A-90°=90°-∠A
20. (1)80;20;20°
(2)解:如图3,∵AD平分∠ABC,
∴∠BAD=∠CAD,
∵AE平分∠BEC,
∴∠AEB=∠AEC,
∵∠C+∠CAE+∠AEC=180°,∠B+∠BAE+∠AEB=180°,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD﹣∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD﹣∠DAE=∠B+∠BAD+∠DAE,
∴2∠DAE=∠C﹣∠B=40°,
∴∠DAE=20°.
(
第
- 1 -
页 共
5
页
)
