人教版九年级上册第24章 圆的有关计算 课件(共40张PPT)
文档属性
| 名称 | 人教版九年级上册第24章 圆的有关计算 课件(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 212.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 07:31:23 | ||
图片预览





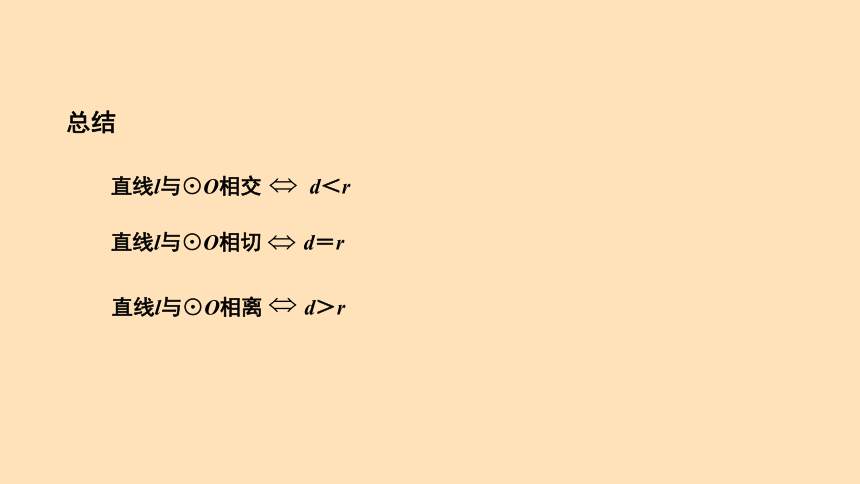


文档简介
(共40张PPT)
圆专题(二)
导入
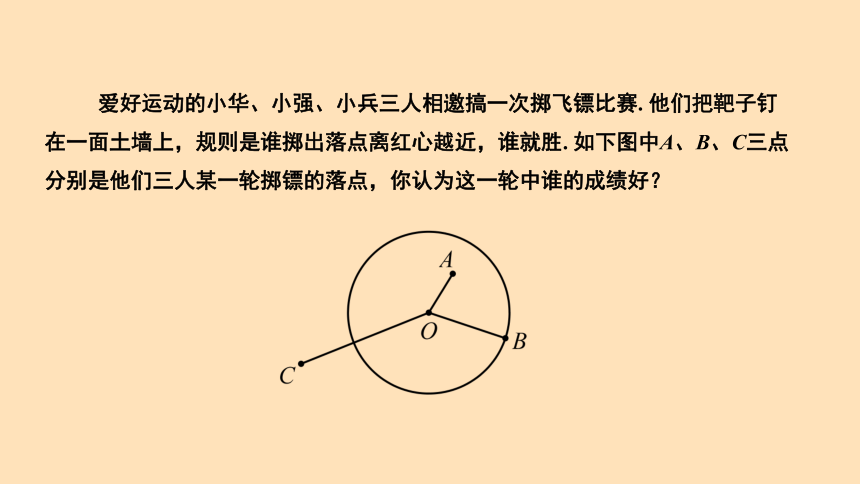
爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛. 他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜. 如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好?
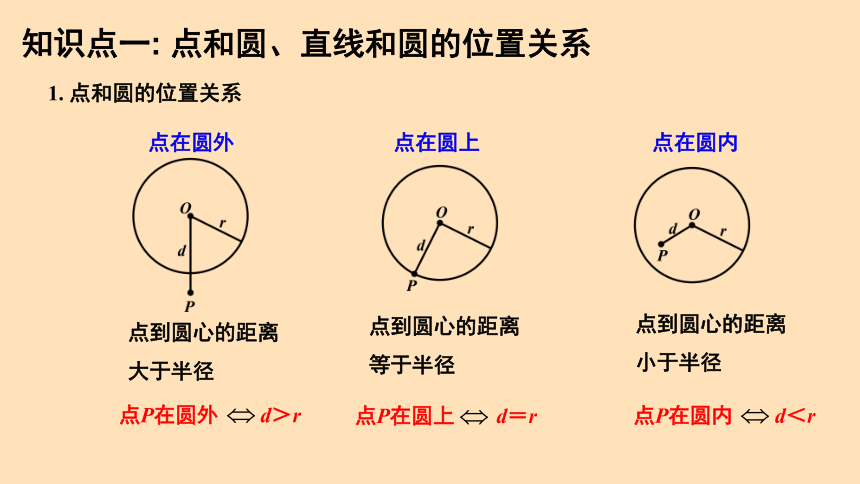
点在圆外
点在圆上
点在圆内
点到圆心的距离大于半径
点到圆心的距离等于半径
点到圆心的距离小于半径
点P在圆外 d>r
点P在圆上 d=r
点P在圆内 d<r
1. 点和圆的位置关系
知识点一: 点和圆、直线和圆的位置关系
2. 确定一个圆的条件
(1)已知圆心、半径,可以确定一个圆;
(2)不在同一条直线上的三个点确定一个圆.
3. 三角形的外接圆
(1)三角形的外接圆:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,这个三角形叫做这个圆的内接三角形.
(2)三角形的外心:三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
(3)三角形外心的性质:三角形的外心到三角形三个顶点的距离相等,等于其外接圆的半径.
(4)三角形外心的位置:锐角三角形的外心在三角形的内部,直角三角形的外心是斜边的中点,钝角三角形的外心在三角形的外部.
4. 反证法
反证法是一种间接证明命题的方法.
假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立. 这种方法叫做反证法.
5. 直线和圆的位置关系
相交:
直线和圆有两个公共点,这时我们说这条直线和圆相交.
相切:
直线和圆只有一个公共点,这时我们说这条直线和圆相切.
相离:
直线和圆没有公共点,这时我们说这条直线和圆相离.
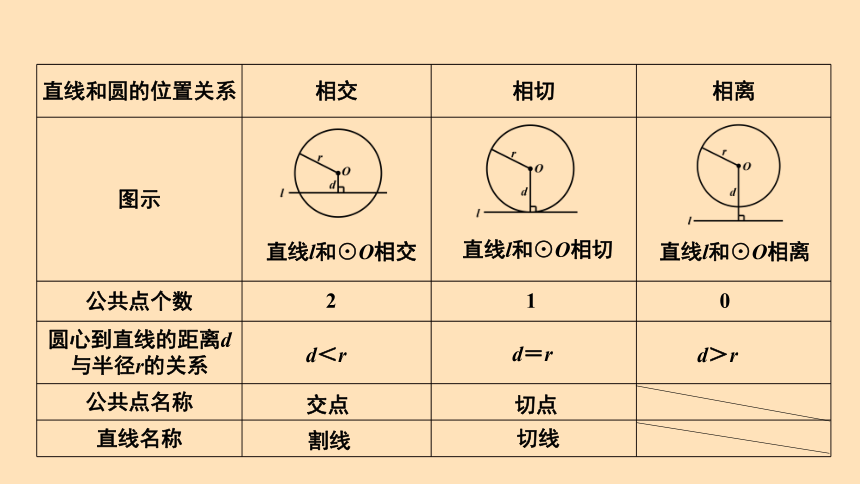
直线和圆的位置关系 相交 相切 相离
图示
公共点个数
圆心到直线的距离d与半径r的关系
公共点名称
直线名称
直线l和⊙O相交
直线l和⊙O相切
直线l和⊙O相离
2
1
0
d<r
d=r
d>r
交点
切点
割线
切线
总结
直线l与⊙O相交 d<r
直线l与⊙O相切 d=r
直线l与⊙O相离 d>r
例1
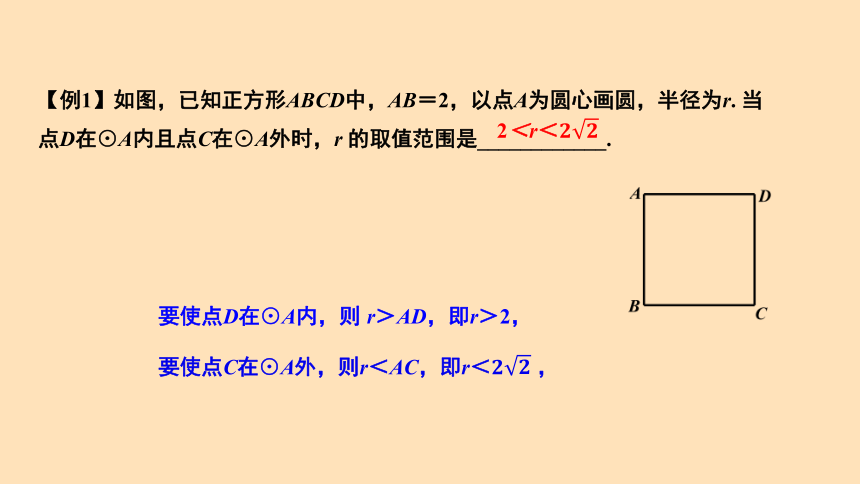
【例1】如图,已知正方形ABCD中,AB=2,以点A为圆心画圆,半径为r. 当点D在⊙A内且点C在⊙A外时,r 的取值范围是____________.
要使点D在⊙A内,则 r>AD,即r>2,
要使点C在⊙A外,则r<AC,即r< ,
2<r<
巩固1
【巩固】
1. 圆的直径为10 cm,若点P 到圆心O的距离是 d,则( )
A. 当d=8 cm时,点P在⊙O内
B. 当d=10 cm时,点P在⊙O上
C. 当d=5 cm时,点P在⊙O上
D. 当d=6 cm时,点P在⊙O内
C
巩固2
【巩固】
2. 已知⊙O的直径为12 cm,圆心到直线 l 的距离5 cm,则直线l与⊙O的公共点的个数为( )
A. 2 B. 1 C. 0 D. 不确定
A
巩固3
【巩固】
3. 如图,在Rt△ABC中,∠ACB=90°,CD=5,D是AB的中点,则它的外接圆的直径为_____________.
10
1. 切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2. 切线的判定方法
(1)定义法:与圆有唯一公共点的直线是圆的切线;
(2)数量法:到圆心的距离等于半径的直线是圆的切线;
(3)判定定理法:经过半径的外端并且垂直于这条半径的直线是圆的切线.
3. 切线的性质定理:圆的切线垂直于过切点的半径.
知识点二:切线的判定和性质
例2
【例2】如图,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连接BC,BC平分∠ABD. 求证:CD为⊙O的切线.
连半径,证垂直
【例2】如图,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连接BC,BC平分∠ABD. 求证:CD为⊙O的切线.
证明:∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠DBC=∠OCB,
∴OC∥BD,
∴∠OCD+∠CDB=180°,
∵BD⊥CD,
∴∠CDB=90°,
∴∠OCD=180°-∠CDB
=180°-90°
=90°.
即OC⊥CD,
又∵OC为半径,
∴CD为⊙O的切线.
巩固1
【巩固】
1. 下列说法中,不正确的是( )
A. 与圆只有一个交点的直线是圆的切线
B. 经过半径的外端,且垂直于这条半径的直线是圆的切线
C. 与圆心的距离等于半径的直线是圆的切线
D. 垂直于半径的直线是圆的切线
D
巩固2
【巩固】
2. 如图,AB是⊙O的直径,MN是⊙O的切线,切点为N,如果∠MNB=52°,则∠NOA的度数为( )
A. 76° B. 56° C. 54° D. 52°
A
1. 切线长
2. 切线长定理
经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的
切线长.
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线
平分两条切线的夹角.
知识点三:切线长定理和三角形的内切圆
3. 三角形的内切圆
4. 三角形的内心
5. 三角形内心的性质
与三角形各边都相切的圆叫做三角形的内切圆,这个三角形叫做这个圆的
外切三角形.
三角形的内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
三角形的内心到三角形三条边的距离相等,且等于其内切圆的半径.
例3
【例3】如图,PA、PB为⊙O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A. PA=PB B. ∠BPD=∠APD
C. AB⊥PD D. AB平分PD
切线长定理
D
三线合一
√
√
√
巩固1
【巩固】
1. 如图,PA,PB分别切⊙O于点A,B,如果∠P=60°,PA=2,那么 AB 的长为( )
A. 1 B. 2 C. 3 D. 4
B
巩固2
【巩固】
2. 如图,点 I 是△ABC 的内心,∠BIC=130°,则 ∠BAC 的度数为( )
A. 60° B. 65° C. 70° D. 80°
D
1. 正多边形及有关概念
(1)正多边形:各边相等、各角也相等的多边形是正多边形.
(2)圆内接正多边形:把圆分成n(n≥3)等份,依次连接各分点得到的多边形就是这个圆的内接正n边形,这个圆就是这个正n边形的外接圆.
知识点四:正多边形和圆
(3)与正多边形有关的概念
名称 定义 图示
中心
半径 中心角 边心距 一个正多边形的外接圆的圆心叫做这个正多边形的中心.
正多边形的外接圆的半径叫做正多边形的半径.
正多边形每一边所对的圆心角叫做正多边形的中心角.
正多边形的中心到正多边形的一边的距离叫做正多边
形的边心距.
(4)正多边形的对称性
所有的正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心,n为偶数时,它还是中心对称图形,它的中心就是对称中心.
2. 正多边形的有关计算
(1)正n边形的每个内角都等于 .
(2)正n边形的每个中心角都等于 .
(3)正n边形的每个外角都等于 .
(4)设正n边形的半径为R,边长为a,边心距为r,则:
①半径、边长、边心距的关系为 ;
②周长l=na;
③面积 .
【例4】如图,边长为12 cm的圆内接正三角形的边心距是_________cm.
x
在Rt△OBH中,由勾股定理得 x2+62=(2x)2,
解得x= .
例4
巩固1
【巩固】
1. 如图,正六边形ABCDEF内接于⊙O,连接OC、OD,则∠COD的大小是( )
A. 30° B. 45° C. 60° D. 90°
C
巩固2
【巩固】
2. 如图,正方形ABCD内接于⊙O,若⊙O的半径是 ,则正方形的边长是________.
2
1. 弧长公式: 在半径为R的圆中,n°的圆心角所对的弧长l的计算公式为 .
2. 扇形:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
3. 扇形面积公式
(1)已知半径R和n°的圆心角,则 .
(2)已知弧长l和半径R,则 .
知识点五:弧长和扇形面积
4. 与圆锥有关的概念
(1)圆锥:圆锥是由一个底面和一个侧面围成的几何体. 圆锥可以看作是一个直角三角形绕它的一条直角边所在的直线旋转一周形成的图形.
(2)圆锥的母线:连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
(3)圆锥的高:连接圆锥顶点与底面圆心的线段叫做圆锥的高.
例5
【例5】如图,已知⊙O的半径是2,点A,B,C 在⊙O上,若四边形OABC是菱形,则图中阴影部分的面积为( )
C
S阴影=2(S扇形OBC-S△OBC)
巩固1
【巩固】
1. 如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的 长为( )
D
巩固2
【巩固】
2. 如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( )
B
课堂总结
课堂总结
1. 点和圆、直线和圆的位置关系
(1)点和圆的位置关系分三种:①点在圆外;②点在圆上;③点在圆内.
(2)确定一个圆的条件
①已知圆心、半径,可以确定一个圆;
②不在同一条直线上的三个点确定一个圆.
课堂总结
(3)三角形的外接圆
①三角形的外心:三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
②三角形外心的性质:三角形的外心到三角形三个顶点的距离相等,等于其外接圆的半径.
(4)直线和圆的位置关系分三种:①相交;②相切;③相离.
课堂总结
2. 切线的判定和性质
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
(2)切线的判定方法(1)定义法;(2)数量法;(3)判定定理法.
(3)切线的性质定理:圆的切线垂直于过切点的半径.
课堂总结
3. 切线长定理和三角形的内切圆
(1)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
(2)三角形的内心:三角形的内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
(3)三角形内心的性质:三角形的内心到三角形三条边的距离相等,且等于其内切圆的半径.
课堂总结
4. 正多边形和圆
(1)正多边形及有关概念:正多边形、圆内接正多边形、中心、半径、中心角、边心距.
(2)正多边形的有关计算.
5. 弧长和扇形面积
(1)弧长公式: .
(2)扇形面积公式:① ;② .
圆专题(二)
导入
爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛. 他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜. 如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好?
点在圆外
点在圆上
点在圆内
点到圆心的距离大于半径
点到圆心的距离等于半径
点到圆心的距离小于半径
点P在圆外 d>r
点P在圆上 d=r
点P在圆内 d<r
1. 点和圆的位置关系
知识点一: 点和圆、直线和圆的位置关系
2. 确定一个圆的条件
(1)已知圆心、半径,可以确定一个圆;
(2)不在同一条直线上的三个点确定一个圆.
3. 三角形的外接圆
(1)三角形的外接圆:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,这个三角形叫做这个圆的内接三角形.
(2)三角形的外心:三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
(3)三角形外心的性质:三角形的外心到三角形三个顶点的距离相等,等于其外接圆的半径.
(4)三角形外心的位置:锐角三角形的外心在三角形的内部,直角三角形的外心是斜边的中点,钝角三角形的外心在三角形的外部.
4. 反证法
反证法是一种间接证明命题的方法.
假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立. 这种方法叫做反证法.
5. 直线和圆的位置关系
相交:
直线和圆有两个公共点,这时我们说这条直线和圆相交.
相切:
直线和圆只有一个公共点,这时我们说这条直线和圆相切.
相离:
直线和圆没有公共点,这时我们说这条直线和圆相离.
直线和圆的位置关系 相交 相切 相离
图示
公共点个数
圆心到直线的距离d与半径r的关系
公共点名称
直线名称
直线l和⊙O相交
直线l和⊙O相切
直线l和⊙O相离
2
1
0
d<r
d=r
d>r
交点
切点
割线
切线
总结
直线l与⊙O相交 d<r
直线l与⊙O相切 d=r
直线l与⊙O相离 d>r
例1
【例1】如图,已知正方形ABCD中,AB=2,以点A为圆心画圆,半径为r. 当点D在⊙A内且点C在⊙A外时,r 的取值范围是____________.
要使点D在⊙A内,则 r>AD,即r>2,
要使点C在⊙A外,则r<AC,即r< ,
2<r<
巩固1
【巩固】
1. 圆的直径为10 cm,若点P 到圆心O的距离是 d,则( )
A. 当d=8 cm时,点P在⊙O内
B. 当d=10 cm时,点P在⊙O上
C. 当d=5 cm时,点P在⊙O上
D. 当d=6 cm时,点P在⊙O内
C
巩固2
【巩固】
2. 已知⊙O的直径为12 cm,圆心到直线 l 的距离5 cm,则直线l与⊙O的公共点的个数为( )
A. 2 B. 1 C. 0 D. 不确定
A
巩固3
【巩固】
3. 如图,在Rt△ABC中,∠ACB=90°,CD=5,D是AB的中点,则它的外接圆的直径为_____________.
10
1. 切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2. 切线的判定方法
(1)定义法:与圆有唯一公共点的直线是圆的切线;
(2)数量法:到圆心的距离等于半径的直线是圆的切线;
(3)判定定理法:经过半径的外端并且垂直于这条半径的直线是圆的切线.
3. 切线的性质定理:圆的切线垂直于过切点的半径.
知识点二:切线的判定和性质
例2
【例2】如图,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连接BC,BC平分∠ABD. 求证:CD为⊙O的切线.
连半径,证垂直
【例2】如图,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连接BC,BC平分∠ABD. 求证:CD为⊙O的切线.
证明:∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠DBC=∠OCB,
∴OC∥BD,
∴∠OCD+∠CDB=180°,
∵BD⊥CD,
∴∠CDB=90°,
∴∠OCD=180°-∠CDB
=180°-90°
=90°.
即OC⊥CD,
又∵OC为半径,
∴CD为⊙O的切线.
巩固1
【巩固】
1. 下列说法中,不正确的是( )
A. 与圆只有一个交点的直线是圆的切线
B. 经过半径的外端,且垂直于这条半径的直线是圆的切线
C. 与圆心的距离等于半径的直线是圆的切线
D. 垂直于半径的直线是圆的切线
D
巩固2
【巩固】
2. 如图,AB是⊙O的直径,MN是⊙O的切线,切点为N,如果∠MNB=52°,则∠NOA的度数为( )
A. 76° B. 56° C. 54° D. 52°
A
1. 切线长
2. 切线长定理
经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的
切线长.
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线
平分两条切线的夹角.
知识点三:切线长定理和三角形的内切圆
3. 三角形的内切圆
4. 三角形的内心
5. 三角形内心的性质
与三角形各边都相切的圆叫做三角形的内切圆,这个三角形叫做这个圆的
外切三角形.
三角形的内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
三角形的内心到三角形三条边的距离相等,且等于其内切圆的半径.
例3
【例3】如图,PA、PB为⊙O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A. PA=PB B. ∠BPD=∠APD
C. AB⊥PD D. AB平分PD
切线长定理
D
三线合一
√
√
√
巩固1
【巩固】
1. 如图,PA,PB分别切⊙O于点A,B,如果∠P=60°,PA=2,那么 AB 的长为( )
A. 1 B. 2 C. 3 D. 4
B
巩固2
【巩固】
2. 如图,点 I 是△ABC 的内心,∠BIC=130°,则 ∠BAC 的度数为( )
A. 60° B. 65° C. 70° D. 80°
D
1. 正多边形及有关概念
(1)正多边形:各边相等、各角也相等的多边形是正多边形.
(2)圆内接正多边形:把圆分成n(n≥3)等份,依次连接各分点得到的多边形就是这个圆的内接正n边形,这个圆就是这个正n边形的外接圆.
知识点四:正多边形和圆
(3)与正多边形有关的概念
名称 定义 图示
中心
半径 中心角 边心距 一个正多边形的外接圆的圆心叫做这个正多边形的中心.
正多边形的外接圆的半径叫做正多边形的半径.
正多边形每一边所对的圆心角叫做正多边形的中心角.
正多边形的中心到正多边形的一边的距离叫做正多边
形的边心距.
(4)正多边形的对称性
所有的正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心,n为偶数时,它还是中心对称图形,它的中心就是对称中心.
2. 正多边形的有关计算
(1)正n边形的每个内角都等于 .
(2)正n边形的每个中心角都等于 .
(3)正n边形的每个外角都等于 .
(4)设正n边形的半径为R,边长为a,边心距为r,则:
①半径、边长、边心距的关系为 ;
②周长l=na;
③面积 .
【例4】如图,边长为12 cm的圆内接正三角形的边心距是_________cm.
x
在Rt△OBH中,由勾股定理得 x2+62=(2x)2,
解得x= .
例4
巩固1
【巩固】
1. 如图,正六边形ABCDEF内接于⊙O,连接OC、OD,则∠COD的大小是( )
A. 30° B. 45° C. 60° D. 90°
C
巩固2
【巩固】
2. 如图,正方形ABCD内接于⊙O,若⊙O的半径是 ,则正方形的边长是________.
2
1. 弧长公式: 在半径为R的圆中,n°的圆心角所对的弧长l的计算公式为 .
2. 扇形:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
3. 扇形面积公式
(1)已知半径R和n°的圆心角,则 .
(2)已知弧长l和半径R,则 .
知识点五:弧长和扇形面积
4. 与圆锥有关的概念
(1)圆锥:圆锥是由一个底面和一个侧面围成的几何体. 圆锥可以看作是一个直角三角形绕它的一条直角边所在的直线旋转一周形成的图形.
(2)圆锥的母线:连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
(3)圆锥的高:连接圆锥顶点与底面圆心的线段叫做圆锥的高.
例5
【例5】如图,已知⊙O的半径是2,点A,B,C 在⊙O上,若四边形OABC是菱形,则图中阴影部分的面积为( )
C
S阴影=2(S扇形OBC-S△OBC)
巩固1
【巩固】
1. 如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的 长为( )
D
巩固2
【巩固】
2. 如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( )
B
课堂总结
课堂总结
1. 点和圆、直线和圆的位置关系
(1)点和圆的位置关系分三种:①点在圆外;②点在圆上;③点在圆内.
(2)确定一个圆的条件
①已知圆心、半径,可以确定一个圆;
②不在同一条直线上的三个点确定一个圆.
课堂总结
(3)三角形的外接圆
①三角形的外心:三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
②三角形外心的性质:三角形的外心到三角形三个顶点的距离相等,等于其外接圆的半径.
(4)直线和圆的位置关系分三种:①相交;②相切;③相离.
课堂总结
2. 切线的判定和性质
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
(2)切线的判定方法(1)定义法;(2)数量法;(3)判定定理法.
(3)切线的性质定理:圆的切线垂直于过切点的半径.
课堂总结
3. 切线长定理和三角形的内切圆
(1)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
(2)三角形的内心:三角形的内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
(3)三角形内心的性质:三角形的内心到三角形三条边的距离相等,且等于其内切圆的半径.
课堂总结
4. 正多边形和圆
(1)正多边形及有关概念:正多边形、圆内接正多边形、中心、半径、中心角、边心距.
(2)正多边形的有关计算.
5. 弧长和扇形面积
(1)弧长公式: .
(2)扇形面积公式:① ;② .
同课章节目录
