人教版九年级上册第24章 圆的有关性质知识点 课件(共35张PPT)
文档属性
| 名称 | 人教版九年级上册第24章 圆的有关性质知识点 课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 328.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 07:34:41 | ||
图片预览







文档简介
(共35张PPT)
课题
圆的有关性质
导入
“一切立体图形中最美的是球,
一切平面图形中最美的是圆”。
————毕达哥拉斯
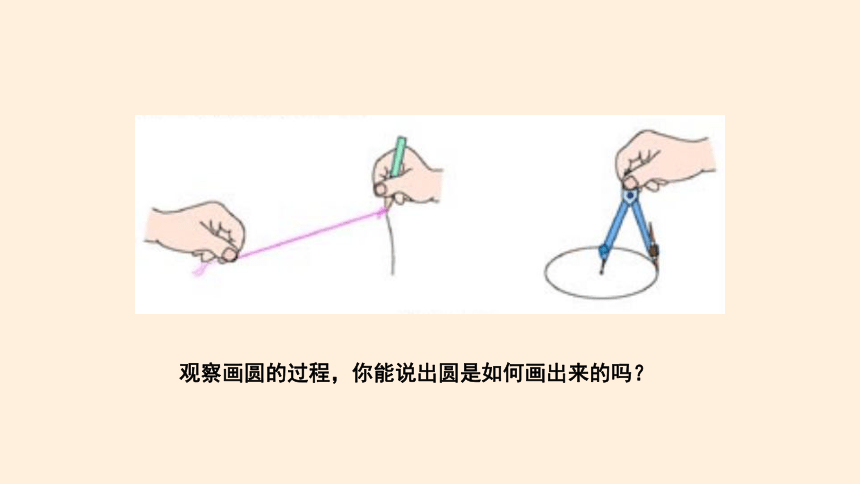
观察画圆的过程,你能说出圆是如何画出来的吗?
固定的端点O叫做圆心.
线段OA叫做半径.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
1. 圆的定义
(1)描述性定义:如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,
另一个端点A所形成的图形叫做圆.
(2)集合性定义:圆可以看成是所有到定点(圆心)的距离
等于定长(半径)的点的集合.
2. 圆的表示方法:
·
O
A
知识点一:圆的有关概念
连接圆上任意两点间的线段.
经过圆心的弦叫直径,是圆中最长的弦.
圆上任意两点间的部分叫做圆弧,简称弧.如 .
小于半圆的弧叫做劣弧.如 .
大于半圆的弧叫优弧.用三个字母表示,如 .
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
半圆:
3. 圆的有关概念
弦:
直径:
弧:
优弧:
劣弧:
等圆:
能够重合的两个圆叫做等圆. 容易看出:半径相等的两个圆叫做等圆;反过来,同圆或等圆的半径相等.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
例1
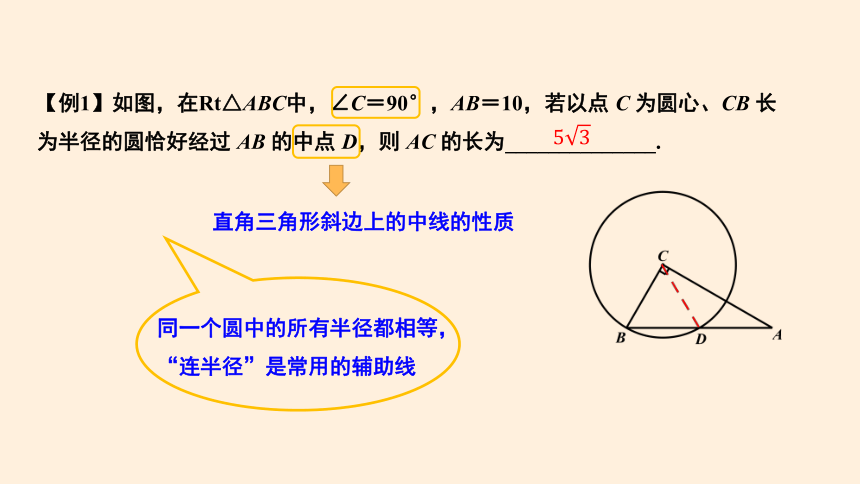
【例1】如图,在Rt△ABC中,∠C=90°,AB=10,若以点 C 为圆心、CB 长为半径的圆恰好经过 AB 的中点 D,则 AC 的长为______________.
同一个圆中的所有半径都相等,“连半径”是常用的辅助线
直角三角形斜边上的中线的性质
巩固1
【巩固】
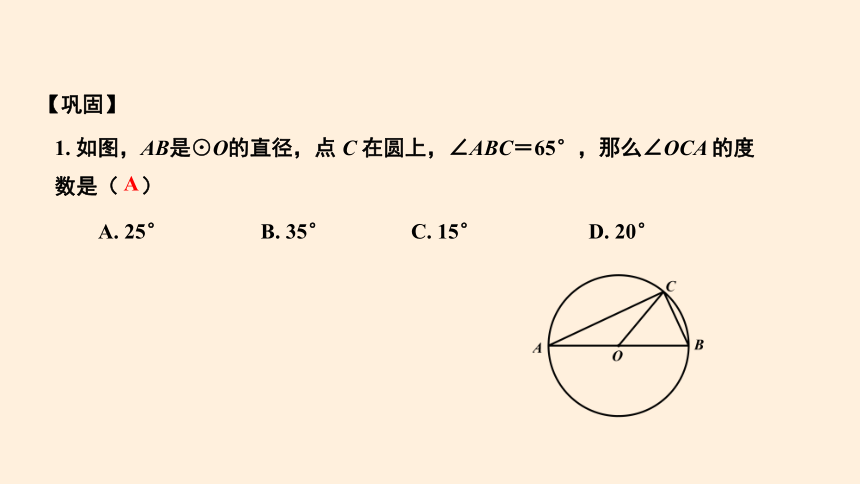
1. 如图,AB是⊙O的直径,点 C 在圆上,∠ABC=65°,那么∠OCA 的度数是( )
A. 25° B. 35° C. 15° D. 20°
A
巩固2
【巩固】
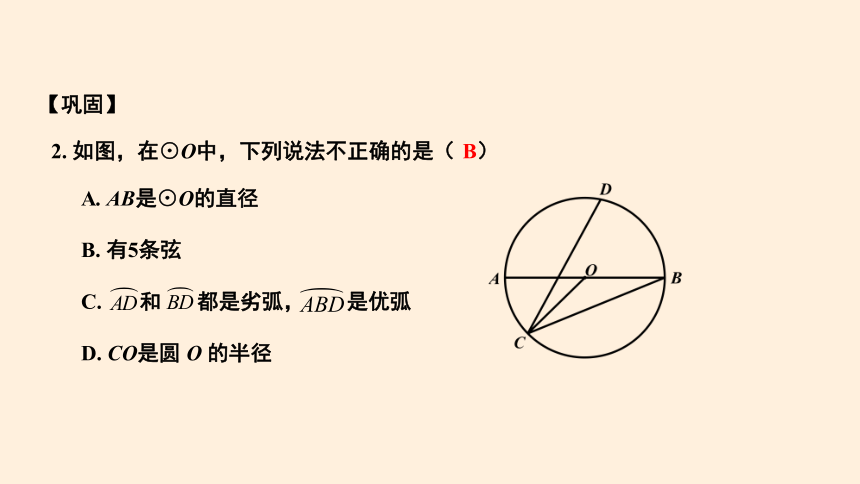
2. 如图,在⊙O中,下列说法不正确的是( )
A. AB是⊙O的直径
B. 有5条弦
C. 和 都是劣弧, 是优弧
D. CO是圆 O 的半径
B
1. 圆的轴对称性
圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
2. 垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
符号语言:
∵如图,CD是直径,CD⊥AB于点M,
∴AM=BM,
= ,
= .
知识点二: 垂直于弦的直径
3. 垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
符号语言:
∵如图,CD是直径,AM=BM(AB不是直径),
∴ CD⊥AB,
= ,
= .
例2
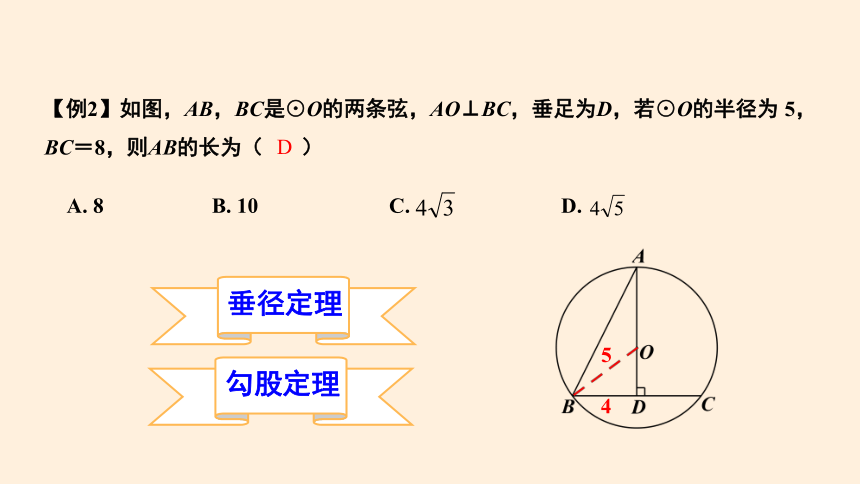
【例2】如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为D,若⊙O的半径为 5,BC=8,则AB的长为( )
A. 8 B. 10 C. D.
D
垂径定理
勾股定理
4
5
巩固1
【巩固】
1. 下列说法不正确的是( )
A. 圆既是轴对称图形又是中心对称图形
B. 圆有无数条对称轴
C. 圆的每一条直径都是它的对称轴
D. 圆的对称中心是它的圆心
C
巩固2
2. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,则AE的长为( )
【巩固】
A. 8 cm B. 5 cm C. 3 cm D. 2 cm
A
1. 圆的旋转对称性
圆具有旋转不变性,把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合. 因此,圆也是中心对称图形,圆心就是它的对称中心.
2. 圆心角的定义
顶点在圆心的角叫做圆心角.
如图:∠AOB是 所对的圆心角, 是∠AOB所对的弧.
知识点三:弧、弦、圆心角
3. 弧、弦、圆心角之间的关系
定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
符号语言:
如图,∵∠AOB=∠COD,
∴ = ,
AB=CD.
重要结论
(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
符号语言:
∴ ∠AOB=∠COD,AB=CD.
如图,∵ = ,
(2)在同圆或等圆中,如果两条弦相等,那么它们所对
的圆心角相等,所对的优弧和劣弧分别相等.
符号语言:
如图,∵ AB=CD,
∴ = , =
∴ ∠AOB=∠COD,
圆心角
弧
弦
知一得二
例3
【例3】如图,点 A,B,C,D 在⊙O 上,且 AB=CD.
求证:AC=BD.
AB=CD
=
知一
得二
等量加等量和相等
=
知一
得二
AC=BD
【例3】如图,点 A,B,C,D 在⊙O 上,且 AB=CD.
求证:AC=BD.
证明:∵AB=CD
∴ =
∴ + = + ,
即 = ,
∴AC=BD.
巩固1
【巩固】
1. 如图,在⊙O 中,∠AOB=∠COD,那么 和 的大小关系是( )
C
巩固2
2. 如图,C是⊙O上的点,CD⊥OA于点 D,CE⊥OB于点 E,且CD=CE,则 与 的关系是( )
【巩固】
A
1. 圆周角的定义
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
2. 圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
如图,∠ACB= ∠AOB.
知识点四:圆周角
3. 圆周角定理的推论
推论1 同弧或等弧所对的圆周角相等.
推论2
(1)半圆(或直径)所对的圆周角是直角;
(2)90°的圆周角所对的弦是直径.
如图,∠C,∠D都是 所对的圆周角,那么∠C=∠D.
如图,若AB为直径,则∠C=∠D=90°.
如图,若∠C=90°或∠D=90°,则AB为直径.
例4
【例4】如图,AB为⊙O的直径,C、D为⊙O上两点,∠BCD=40°,
则∠ABD的大小为( )
A. 60° B. 50° C. 40° D. 20°
B
巩固1
【巩固】
1. 如图,点 A,B,C 在⊙O上,若∠OAB=54°,则∠C 的度数为( )
A. 54° B. 46° C. 36° D. 27°
C
巩固2
2. 如图,点A,B,C,D在⊙O上, = ,∠CAD=30°,∠ACD=50°,则∠ADB=___________.
【巩固】
70°
1. 圆内接多边形的定义
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
2. 圆内接四边形的性质
圆内接四边形的对角互补.
注意:每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.
知识点五:圆内接多边形
例5
【例5】如图,四边形ABCD 为⊙O 的内接四边形,E 是BC 延长线上的一点,已知∠BOD=130°,则∠DCE 的度数为( )
A. 45° B. 50° C. 65° D. 75°
130°
65°
115°
C
巩固1
【巩固】
1. 如图,在⊙O中,∠AOB=120°,P为劣弧 上的一点,则∠APB的度数
是_____________.
120°
巩固2
【巩固】
2. 如图,四边形ABCD为⊙O 的内接四边形,已知∠C=∠D. 问AB与CD有怎样的位置关系,请说明理由.
解:AB∥CD
理由如下:∵四边形ABCD为⊙O的内接四边形,
∴∠A+∠C=180°,
∵∠C=∠D,
∴∠A+∠D=180°,
∴AB∥CD.
课堂巩固
1. 圆的有关概念
(1)圆的定义:①描述性定义;②集合性定义.
(2)圆的表示方法:以点O为圆心的圆,记作⊙O,读作“圆O”.
(3)圆的有关概念:弦、直径、弧、半圆、劣弧、优弧、等圆、等弧.
课堂总结
2. 垂直于弦的直径
课堂总结
(1)垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并
且平分弦所对的两条弧.
3. 弧、弦、圆心角
(1)定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
(2)重要结论
①在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
②在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
课堂总结
4. 圆周角
课堂总结
(1)圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
(2)圆周角定理的推论
推论1 同弧或等弧所对的圆周角相等.
推论2 ①半圆(或直径)所对的圆周角是直角;
②90°的圆周角所对的弦是直径.
5. 圆内接多边形的性质:圆内接四边形的对角互补.
课题
圆的有关性质
导入
“一切立体图形中最美的是球,
一切平面图形中最美的是圆”。
————毕达哥拉斯
观察画圆的过程,你能说出圆是如何画出来的吗?
固定的端点O叫做圆心.
线段OA叫做半径.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
1. 圆的定义
(1)描述性定义:如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,
另一个端点A所形成的图形叫做圆.
(2)集合性定义:圆可以看成是所有到定点(圆心)的距离
等于定长(半径)的点的集合.
2. 圆的表示方法:
·
O
A
知识点一:圆的有关概念
连接圆上任意两点间的线段.
经过圆心的弦叫直径,是圆中最长的弦.
圆上任意两点间的部分叫做圆弧,简称弧.如 .
小于半圆的弧叫做劣弧.如 .
大于半圆的弧叫优弧.用三个字母表示,如 .
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
半圆:
3. 圆的有关概念
弦:
直径:
弧:
优弧:
劣弧:
等圆:
能够重合的两个圆叫做等圆. 容易看出:半径相等的两个圆叫做等圆;反过来,同圆或等圆的半径相等.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
例1
【例1】如图,在Rt△ABC中,∠C=90°,AB=10,若以点 C 为圆心、CB 长为半径的圆恰好经过 AB 的中点 D,则 AC 的长为______________.
同一个圆中的所有半径都相等,“连半径”是常用的辅助线
直角三角形斜边上的中线的性质
巩固1
【巩固】
1. 如图,AB是⊙O的直径,点 C 在圆上,∠ABC=65°,那么∠OCA 的度数是( )
A. 25° B. 35° C. 15° D. 20°
A
巩固2
【巩固】
2. 如图,在⊙O中,下列说法不正确的是( )
A. AB是⊙O的直径
B. 有5条弦
C. 和 都是劣弧, 是优弧
D. CO是圆 O 的半径
B
1. 圆的轴对称性
圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
2. 垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
符号语言:
∵如图,CD是直径,CD⊥AB于点M,
∴AM=BM,
= ,
= .
知识点二: 垂直于弦的直径
3. 垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
符号语言:
∵如图,CD是直径,AM=BM(AB不是直径),
∴ CD⊥AB,
= ,
= .
例2
【例2】如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为D,若⊙O的半径为 5,BC=8,则AB的长为( )
A. 8 B. 10 C. D.
D
垂径定理
勾股定理
4
5
巩固1
【巩固】
1. 下列说法不正确的是( )
A. 圆既是轴对称图形又是中心对称图形
B. 圆有无数条对称轴
C. 圆的每一条直径都是它的对称轴
D. 圆的对称中心是它的圆心
C
巩固2
2. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,则AE的长为( )
【巩固】
A. 8 cm B. 5 cm C. 3 cm D. 2 cm
A
1. 圆的旋转对称性
圆具有旋转不变性,把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合. 因此,圆也是中心对称图形,圆心就是它的对称中心.
2. 圆心角的定义
顶点在圆心的角叫做圆心角.
如图:∠AOB是 所对的圆心角, 是∠AOB所对的弧.
知识点三:弧、弦、圆心角
3. 弧、弦、圆心角之间的关系
定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
符号语言:
如图,∵∠AOB=∠COD,
∴ = ,
AB=CD.
重要结论
(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
符号语言:
∴ ∠AOB=∠COD,AB=CD.
如图,∵ = ,
(2)在同圆或等圆中,如果两条弦相等,那么它们所对
的圆心角相等,所对的优弧和劣弧分别相等.
符号语言:
如图,∵ AB=CD,
∴ = , =
∴ ∠AOB=∠COD,
圆心角
弧
弦
知一得二
例3
【例3】如图,点 A,B,C,D 在⊙O 上,且 AB=CD.
求证:AC=BD.
AB=CD
=
知一
得二
等量加等量和相等
=
知一
得二
AC=BD
【例3】如图,点 A,B,C,D 在⊙O 上,且 AB=CD.
求证:AC=BD.
证明:∵AB=CD
∴ =
∴ + = + ,
即 = ,
∴AC=BD.
巩固1
【巩固】
1. 如图,在⊙O 中,∠AOB=∠COD,那么 和 的大小关系是( )
C
巩固2
2. 如图,C是⊙O上的点,CD⊥OA于点 D,CE⊥OB于点 E,且CD=CE,则 与 的关系是( )
【巩固】
A
1. 圆周角的定义
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
2. 圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
如图,∠ACB= ∠AOB.
知识点四:圆周角
3. 圆周角定理的推论
推论1 同弧或等弧所对的圆周角相等.
推论2
(1)半圆(或直径)所对的圆周角是直角;
(2)90°的圆周角所对的弦是直径.
如图,∠C,∠D都是 所对的圆周角,那么∠C=∠D.
如图,若AB为直径,则∠C=∠D=90°.
如图,若∠C=90°或∠D=90°,则AB为直径.
例4
【例4】如图,AB为⊙O的直径,C、D为⊙O上两点,∠BCD=40°,
则∠ABD的大小为( )
A. 60° B. 50° C. 40° D. 20°
B
巩固1
【巩固】
1. 如图,点 A,B,C 在⊙O上,若∠OAB=54°,则∠C 的度数为( )
A. 54° B. 46° C. 36° D. 27°
C
巩固2
2. 如图,点A,B,C,D在⊙O上, = ,∠CAD=30°,∠ACD=50°,则∠ADB=___________.
【巩固】
70°
1. 圆内接多边形的定义
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
2. 圆内接四边形的性质
圆内接四边形的对角互补.
注意:每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.
知识点五:圆内接多边形
例5
【例5】如图,四边形ABCD 为⊙O 的内接四边形,E 是BC 延长线上的一点,已知∠BOD=130°,则∠DCE 的度数为( )
A. 45° B. 50° C. 65° D. 75°
130°
65°
115°
C
巩固1
【巩固】
1. 如图,在⊙O中,∠AOB=120°,P为劣弧 上的一点,则∠APB的度数
是_____________.
120°
巩固2
【巩固】
2. 如图,四边形ABCD为⊙O 的内接四边形,已知∠C=∠D. 问AB与CD有怎样的位置关系,请说明理由.
解:AB∥CD
理由如下:∵四边形ABCD为⊙O的内接四边形,
∴∠A+∠C=180°,
∵∠C=∠D,
∴∠A+∠D=180°,
∴AB∥CD.
课堂巩固
1. 圆的有关概念
(1)圆的定义:①描述性定义;②集合性定义.
(2)圆的表示方法:以点O为圆心的圆,记作⊙O,读作“圆O”.
(3)圆的有关概念:弦、直径、弧、半圆、劣弧、优弧、等圆、等弧.
课堂总结
2. 垂直于弦的直径
课堂总结
(1)垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并
且平分弦所对的两条弧.
3. 弧、弦、圆心角
(1)定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
(2)重要结论
①在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
②在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
课堂总结
4. 圆周角
课堂总结
(1)圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
(2)圆周角定理的推论
推论1 同弧或等弧所对的圆周角相等.
推论2 ①半圆(或直径)所对的圆周角是直角;
②90°的圆周角所对的弦是直径.
5. 圆内接多边形的性质:圆内接四边形的对角互补.
同课章节目录
