冀教版九年级下册30.2 二次函数的图像和性质(第二课时) 课件 (共24张PPT)
文档属性
| 名称 | 冀教版九年级下册30.2 二次函数的图像和性质(第二课时) 课件 (共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 07:47:03 | ||
图片预览



文档简介
(共24张PPT)
30.2 二次函数的图像和性质
第三十章 二次函数
冀教版九下
第2课时 二次函数 y=a(x-h) +k 的图像和性质
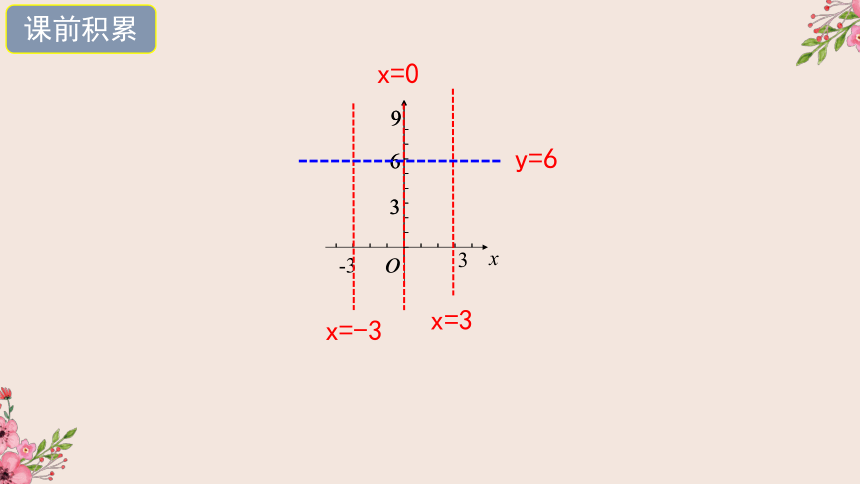
课前积累
a对抛物线y=ax 的影响
a>0时,抛物线开口向上
1.a的正负
a<0时,抛物线开口向下
2.a的绝对值
a的绝对值越大,抛物线开口越小
a的绝对值越小,抛物线开口越大
开口方向
开口大小
o
9
-3
3
6
9
3
3
6
x
x=3
x=-3
x=0
y=6
课前积累
新课学习
探究:
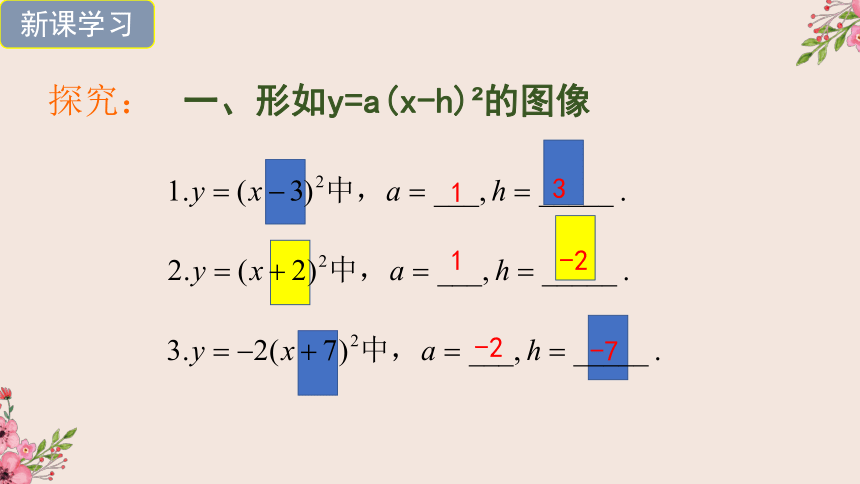
一、形如y=a(x-h) 的图像
1
3
1
-2
-2
-7
新课学习
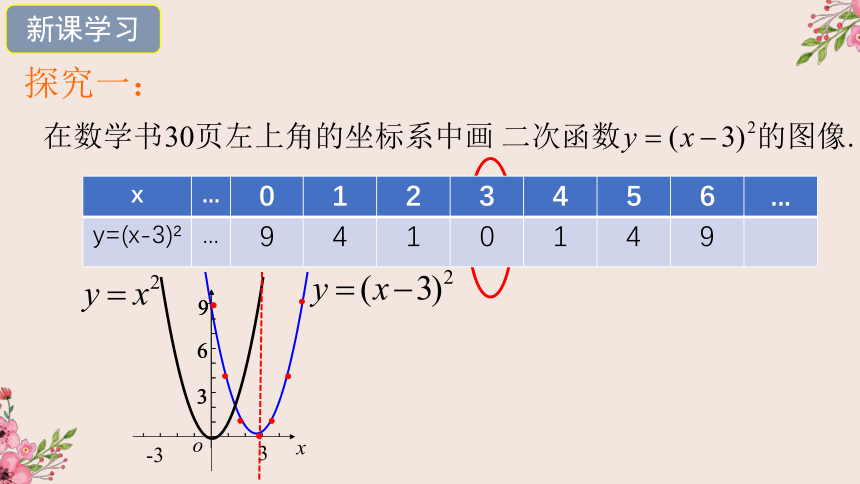
探究一:
x ... 0 1 2 3 4 5 6 ...
y=(x-3) ... 9 4 1 0 1 4 9
o
9
-3
3
6
9
3
3
6
x
新课学习
观察:
1.y=(x-3) 的对称轴:
顶点:
o
9
-3
3
6
9
3
3
6
x
直线x=3
(3,0)
2.抛物线y=x 向____平移___个单位长度可得到的y=(x-3) .
让抛物线动起来
右
3
x=3
3.抛物线y=(x-3) 向____平移___个单位长度可得到的y=x .
左
3
规则:
左加右减
新课学习
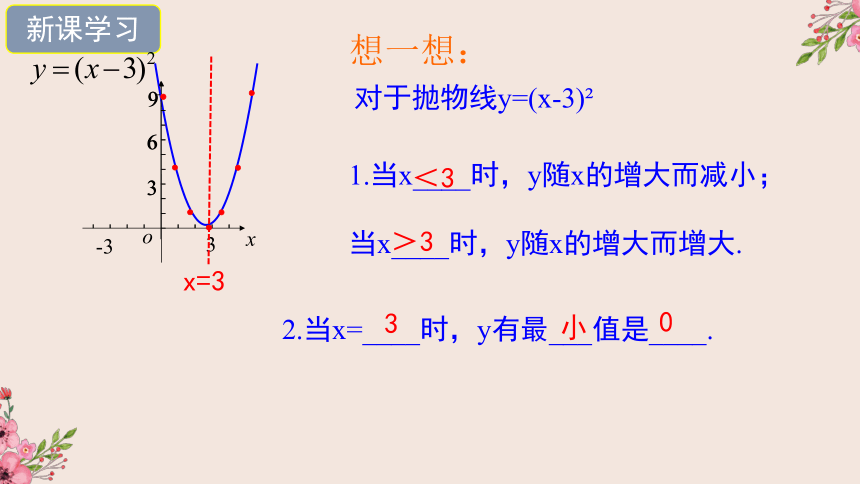
想一想:
o
9
-3
3
6
9
3
3
6
x
3
2.当x=____时,y有最___值是____.
x=3
对于抛物线y=(x-3)
1.当x____时,y随x的增大而减小;
当x____时,y随x的增大而增大.
<3
>3
小
0
新课学习
探究一:
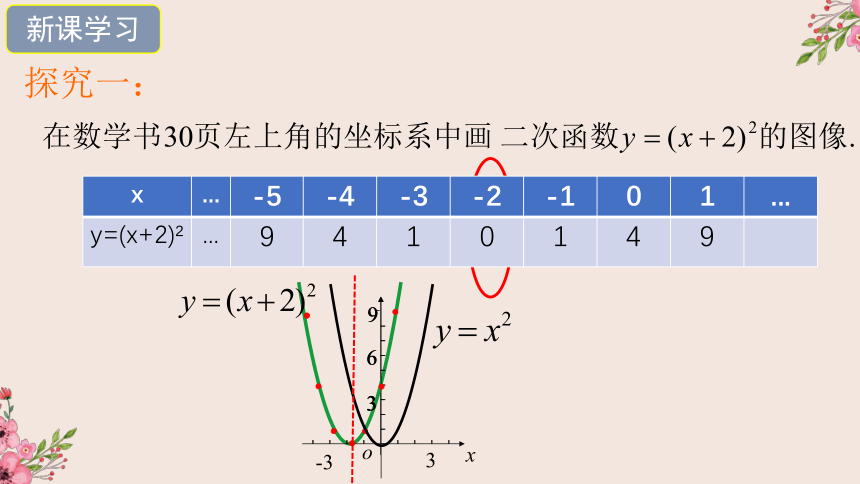
x ... -5 -4 -3 -2 -1 0 1 ...
y=(x+2) ... 9 4 1 0 1 4 9
o
9
-3
3
6
9
3
3
6
x
新课学习
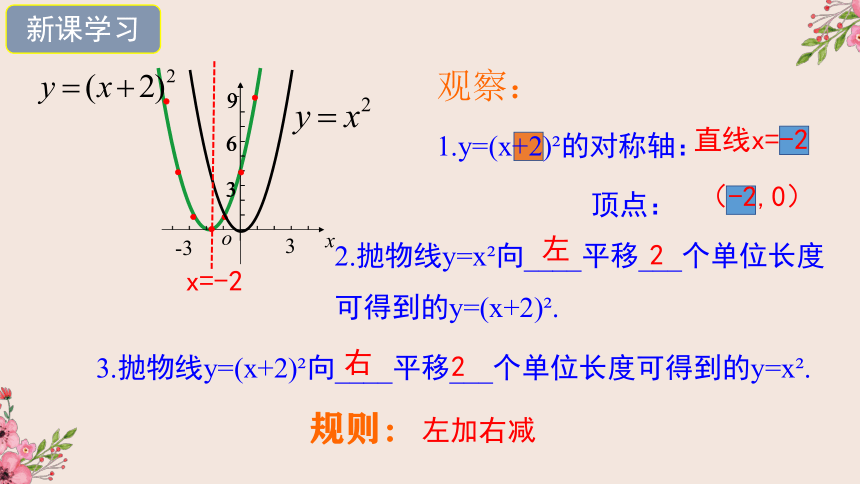
观察:
1.y=(x+2) 的对称轴:
顶点:
直线x=-2
(-2,0)
o
9
-3
3
6
9
3
3
6
x
x=-2
规则:
左加右减
2.抛物线y=x 向____平移___个单位长度可得到的y=(x+2) .
左
2
3.抛物线y=(x+2) 向____平移___个单位长度可得到的y=x .
右
2
新课学习
想一想:
-2
2.当x=____时,y有最___值是____.
x=-2
对于抛物线y=(x+2)
1.当x____时,y随x的增大而减小;
当x____时,y随x的增大而增大.
<-2
>-2
小
0
o
9
-3
3
6
9
3
3
6
x
新课学习
总结:
1.二次函数y=a(x-h)
对称轴是 ,
顶点坐标是 .
让抛物线动起来
直线x=h
(h,0)
2.抛物线y=a(x-h) 可由y=ax ____平移得到.
左右
规则:
左加右减
新课学习
想一想:
1.抛物线y=-2(x-3) 向左平移8个单位可得到抛物线y=____________.
2.抛物线y=5(x+3) 向___平移___个单位可得到抛物线y=5(x+1) .
右
2
-2(x+5)
规则:
左加右减
新课学习
二、形如y=a(x-h)2+k的图像
想一想:
1
-2
-1
2.画y=(x+2) -1的图像时,下表中的取值合适吗?
x ... -3 -2 -1 0 1 2 3 ...
y=(x+2) -1 ... 0 -1 0 3 8 15 24
不合适.不能体现抛物线的对称性.
新课学习
o
9
-3
3
6
3
3
x
新课学习
探究二:
x ... -5 -4 -3 -2 -1 0 1 ...
y=(x+2) -1 ... 8 3 0 -1 0 3 8
o
9
-3
3
6
9
3
3
6
x
新课学习
观察:
1.y=(x+2) -1的对称轴:
顶点:
直线x=-2
(-2,-1)
2.抛物线y=(x+2) -1可看做由y=(x+2) 向____平移了___个单位长度得到的.
上加下减
下
1
抛物线y=(x-1) +3的对称轴是________,顶点是_______,可看做由y=(x-1) 向____平移了___个单位长度得到的.
想一想:
直线x=1
(1,3)
上
3
o
9
-3
3
6
9
3
3
6
x
x=-2
规则:
新课学习
想一想:
-2
2.当x=____时,y有最___值是____.
x=-2
对于抛物线y=(x+2) -1
1.当x____时,y随x的增大而减小;
当x____时,y随x的增大而增大.
<-2
>-2
小
-1
o
9
-3
3
6
9
3
3
6
x
新课学习
1.已知抛物线y= -2(x+1)2-2.
①开口方向______.
②对称轴是_______
③顶点坐标是_______.
④当x_____时,y随x的增大而增大.
⑤当x=____时,y有最___值是_____.
⑥可看做有y=-2x 怎样平移得到?
探究三:
向下
直线x=-1
(-1,-2)
大
-1
<-1
-2
左1
下2
巩固总结
h
﹥h
向上
﹤h
直线 x = h
( h,k )
二次函数y=a(x-h)2 +k的特点
顶点式
对称轴: ;顶点坐标:
当a﹥0时,开口_____;当x_____时,y随x的增大而减小,当x_____时,y随x的增大而增大.
当x=____时,y有最___值是_____.
小
k
巩固总结
h
增大
向下
减小
直线 x = h
( h,k )
二次函数y=a(x-h)2 +k的特点
顶点式
对称轴: ;定点坐标:
当a﹤0时,开口_____;当x﹤h时,y随x的增大而____,当x﹥h时,y随x的增大而_____.
当x=____时,y有最___值是_____.
大
k
典例精析
例1.若(-20,y1)(-3,y2)(4 ,y3)为二次函数y=(x-2)2图像上的三点,则y1 ,y2 ,y3的大小关系为_______________.
将x=-20,x=-3,x=4带入函数表达式中,求出相应的y值分别为484,25,4.
方法一:
典例精析
例1.若A(-20,y1)B(-3,y2)C(4 ,y3)为二次函数y=(x-2)2图像上的三点,则y1 ,y2 ,y3的大小关系为_______________.
∵a=1>0,
∴x=2时,y值最小.
∴x的值与2越接近,则y值越小
∵点A,B,C与对称轴x=2的距离分别是22,5,2.
方法二:
拓展延伸
∵a=1>0,∴x=h时,y值最小为1.
已知中y的最小值为5,则说明顶点没有在取值范围之内.
当1≤x≤3在对称轴左侧时,y随x的增大而减小
∴x=3时,y有最小值5,代入可求得h=5.
当1≤x≤3在对称轴右侧时,y随x的增大而增大
∴x=1时,y有最小值5,代入可求得h=-1.
分析:
已知抛物线y =(x-h)2+1,在自变量x满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为_____.
-1或5
同学们再见
30.2 二次函数的图像和性质
第三十章 二次函数
冀教版九下
第2课时 二次函数 y=a(x-h) +k 的图像和性质
课前积累
a对抛物线y=ax 的影响
a>0时,抛物线开口向上
1.a的正负
a<0时,抛物线开口向下
2.a的绝对值
a的绝对值越大,抛物线开口越小
a的绝对值越小,抛物线开口越大
开口方向
开口大小
o
9
-3
3
6
9
3
3
6
x
x=3
x=-3
x=0
y=6
课前积累
新课学习
探究:
一、形如y=a(x-h) 的图像
1
3
1
-2
-2
-7
新课学习
探究一:
x ... 0 1 2 3 4 5 6 ...
y=(x-3) ... 9 4 1 0 1 4 9
o
9
-3
3
6
9
3
3
6
x
新课学习
观察:
1.y=(x-3) 的对称轴:
顶点:
o
9
-3
3
6
9
3
3
6
x
直线x=3
(3,0)
2.抛物线y=x 向____平移___个单位长度可得到的y=(x-3) .
让抛物线动起来
右
3
x=3
3.抛物线y=(x-3) 向____平移___个单位长度可得到的y=x .
左
3
规则:
左加右减
新课学习
想一想:
o
9
-3
3
6
9
3
3
6
x
3
2.当x=____时,y有最___值是____.
x=3
对于抛物线y=(x-3)
1.当x____时,y随x的增大而减小;
当x____时,y随x的增大而增大.
<3
>3
小
0
新课学习
探究一:
x ... -5 -4 -3 -2 -1 0 1 ...
y=(x+2) ... 9 4 1 0 1 4 9
o
9
-3
3
6
9
3
3
6
x
新课学习
观察:
1.y=(x+2) 的对称轴:
顶点:
直线x=-2
(-2,0)
o
9
-3
3
6
9
3
3
6
x
x=-2
规则:
左加右减
2.抛物线y=x 向____平移___个单位长度可得到的y=(x+2) .
左
2
3.抛物线y=(x+2) 向____平移___个单位长度可得到的y=x .
右
2
新课学习
想一想:
-2
2.当x=____时,y有最___值是____.
x=-2
对于抛物线y=(x+2)
1.当x____时,y随x的增大而减小;
当x____时,y随x的增大而增大.
<-2
>-2
小
0
o
9
-3
3
6
9
3
3
6
x
新课学习
总结:
1.二次函数y=a(x-h)
对称轴是 ,
顶点坐标是 .
让抛物线动起来
直线x=h
(h,0)
2.抛物线y=a(x-h) 可由y=ax ____平移得到.
左右
规则:
左加右减
新课学习
想一想:
1.抛物线y=-2(x-3) 向左平移8个单位可得到抛物线y=____________.
2.抛物线y=5(x+3) 向___平移___个单位可得到抛物线y=5(x+1) .
右
2
-2(x+5)
规则:
左加右减
新课学习
二、形如y=a(x-h)2+k的图像
想一想:
1
-2
-1
2.画y=(x+2) -1的图像时,下表中的取值合适吗?
x ... -3 -2 -1 0 1 2 3 ...
y=(x+2) -1 ... 0 -1 0 3 8 15 24
不合适.不能体现抛物线的对称性.
新课学习
o
9
-3
3
6
3
3
x
新课学习
探究二:
x ... -5 -4 -3 -2 -1 0 1 ...
y=(x+2) -1 ... 8 3 0 -1 0 3 8
o
9
-3
3
6
9
3
3
6
x
新课学习
观察:
1.y=(x+2) -1的对称轴:
顶点:
直线x=-2
(-2,-1)
2.抛物线y=(x+2) -1可看做由y=(x+2) 向____平移了___个单位长度得到的.
上加下减
下
1
抛物线y=(x-1) +3的对称轴是________,顶点是_______,可看做由y=(x-1) 向____平移了___个单位长度得到的.
想一想:
直线x=1
(1,3)
上
3
o
9
-3
3
6
9
3
3
6
x
x=-2
规则:
新课学习
想一想:
-2
2.当x=____时,y有最___值是____.
x=-2
对于抛物线y=(x+2) -1
1.当x____时,y随x的增大而减小;
当x____时,y随x的增大而增大.
<-2
>-2
小
-1
o
9
-3
3
6
9
3
3
6
x
新课学习
1.已知抛物线y= -2(x+1)2-2.
①开口方向______.
②对称轴是_______
③顶点坐标是_______.
④当x_____时,y随x的增大而增大.
⑤当x=____时,y有最___值是_____.
⑥可看做有y=-2x 怎样平移得到?
探究三:
向下
直线x=-1
(-1,-2)
大
-1
<-1
-2
左1
下2
巩固总结
h
﹥h
向上
﹤h
直线 x = h
( h,k )
二次函数y=a(x-h)2 +k的特点
顶点式
对称轴: ;顶点坐标:
当a﹥0时,开口_____;当x_____时,y随x的增大而减小,当x_____时,y随x的增大而增大.
当x=____时,y有最___值是_____.
小
k
巩固总结
h
增大
向下
减小
直线 x = h
( h,k )
二次函数y=a(x-h)2 +k的特点
顶点式
对称轴: ;定点坐标:
当a﹤0时,开口_____;当x﹤h时,y随x的增大而____,当x﹥h时,y随x的增大而_____.
当x=____时,y有最___值是_____.
大
k
典例精析
例1.若(-20,y1)(-3,y2)(4 ,y3)为二次函数y=(x-2)2图像上的三点,则y1 ,y2 ,y3的大小关系为_______________.
将x=-20,x=-3,x=4带入函数表达式中,求出相应的y值分别为484,25,4.
方法一:
典例精析
例1.若A(-20,y1)B(-3,y2)C(4 ,y3)为二次函数y=(x-2)2图像上的三点,则y1 ,y2 ,y3的大小关系为_______________.
∵a=1>0,
∴x=2时,y值最小.
∴x的值与2越接近,则y值越小
∵点A,B,C与对称轴x=2的距离分别是22,5,2.
方法二:
拓展延伸
∵a=1>0,∴x=h时,y值最小为1.
已知中y的最小值为5,则说明顶点没有在取值范围之内.
当1≤x≤3在对称轴左侧时,y随x的增大而减小
∴x=3时,y有最小值5,代入可求得h=5.
当1≤x≤3在对称轴右侧时,y随x的增大而增大
∴x=1时,y有最小值5,代入可求得h=-1.
分析:
已知抛物线y =(x-h)2+1,在自变量x满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为_____.
-1或5
同学们再见
