计数原理复习小结
图片预览








文档简介
课件40张PPT。计数原理基
本
原
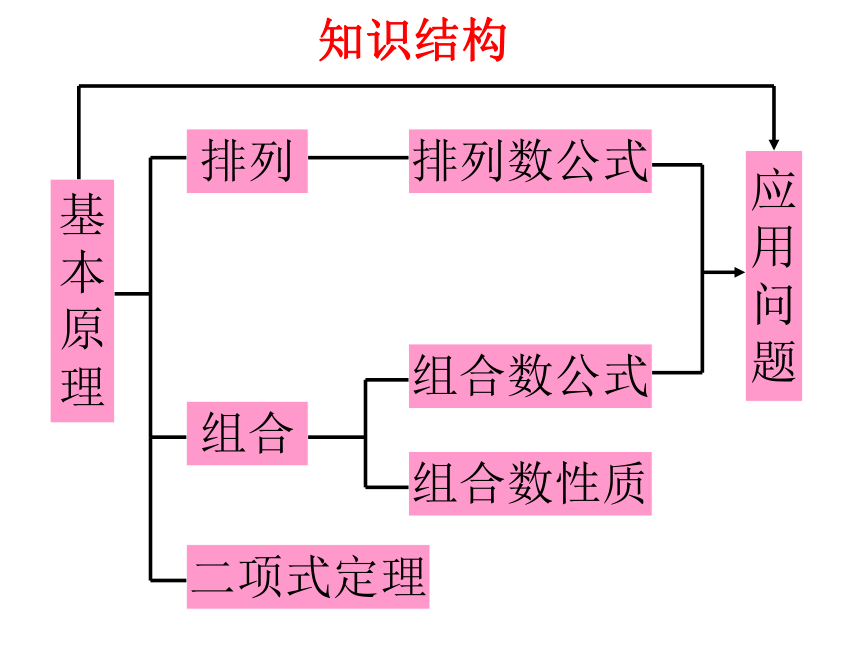
理组合排列排列数公式组合数公式组合数性质应
用
问
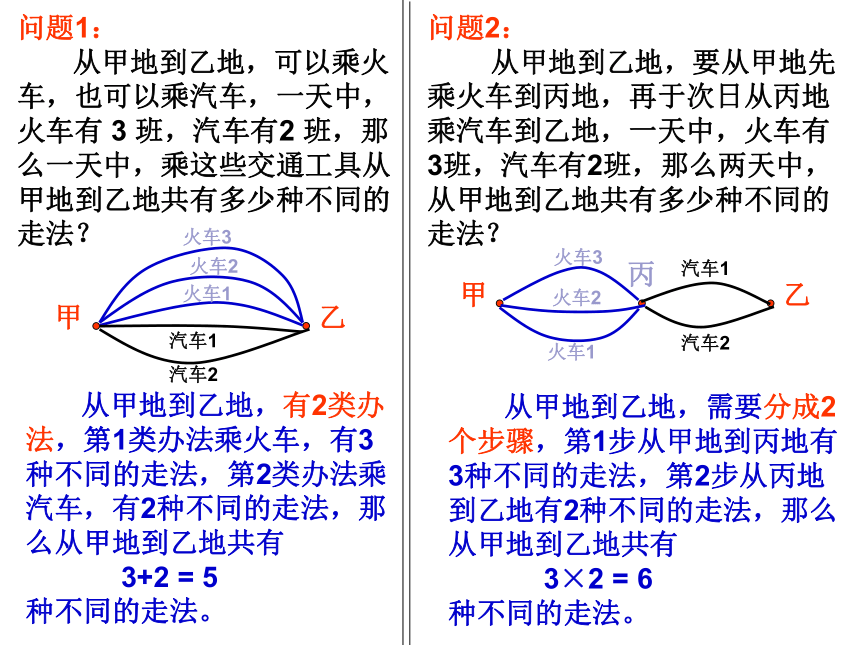
题知识结构二项式定理分类计数原理 完成一件事,有n类办法,在第1类办法中,有m1种不同的方法,在第2类办法中,有m2种不同的方法……在第n类办法中,有mn种不同的方法,则完成这件事有N=m1+m2+ ……+mn种不同的方法分步计数原理 完成一件事,需要分成n个步骤,在第1步中,有m1种不同的方法,在第2步中,有m2种不同的方法……在第n步中,有mn种不同的方法,则完成这件事有N=m1×m2× ……×mn种不同的方法两个基本原理问题1:
从甲地到乙地,可以乘火
车,也可以乘汽车,一天中,
火车有 3 班,汽车有2 班,那
么一天中,乘这些交通工具从
甲地到乙地共有多少种不同的
走法?问题2:
从甲地到乙地,要从甲地先
乘火车到丙地,再于次日从丙地
乘汽车到乙地,一天中,火车有
3班,汽车有2班,那么两天中,
从甲地到乙地共有多少种不同的
走法? 从甲地到乙地,有2类办
法,第1类办法乘火车,有3
种不同的走法,第2类办法乘
汽车,有2种不同的走法,那
么从甲地到乙地共有
3+2 = 5
种不同的走法。 从甲地到乙地,需要分成2
个步骤,第1步从甲地到丙地有
3种不同的走法,第2步从丙地
到乙地有2种不同的走法,那么
从甲地到乙地共有
3×2 = 6
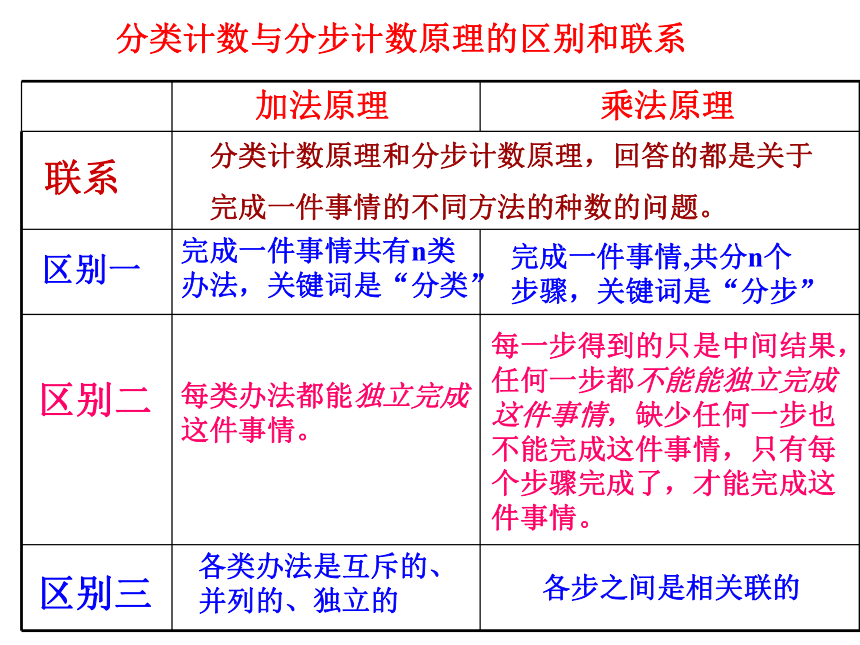
种不同的走法。联系区别一完成一件事情共有n类
办法,关键词是“分类”完成一件事情,共分n个
步骤,关键词是“分步”
区别二
每类办法都能独立完成
这件事情。每一步得到的只是中间结果,
任何一步都不能能独立完成
这件事情,缺少任何一步也
不能完成这件事情,只有每
个步骤完成了,才能完成这
件事情。
分类计数原理和分步计数原理,回答的都是关于
完成一件事情的不同方法的种数的问题。
区别三各类办法是互斥的、
并列的、独立的各步之间是相关联的分类计数与分步计数原理的区别和联系1.某校组织学生分4个组从3处风景点中选一处去春游,则不同的春游方案的种数是( )2.某校组织学生分3个组从4处风景点中选一处去春游,则不同的春游方案的种数是( )典型例题从n个不同元素中,任取m个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.1.排列的定义:从n个不同元素中,任取m个元素,合成一组,叫做从n个不同元素中取出m个元素的一个组合.2.组合的定义:排列组合④两个组合的元素完全相同为相同组合排列数、组合数计算公式组合数的两个性质性质1性质2有特殊元素和特殊位置的排列问题例:用0到9这10个数字可以组成多少个没有重复数字的三位数? 特殊位置“百位”,特殊元素“0”特殊位置优先安排特殊元素优先考虑正难则反(间接法)相邻问题例:4男3女排成一排,三个女生排在一起,有多少种不同排法?对于相邻问题,常用“捆绑法”★ 某些元素要求必须相邻时,可以先将这些元素看作一个元素,与其他元素排列后,再考虑相邻元素的内部排列,这种方法称为“捆绑法”;
相邻问题捆绑处理的策略例:4男3女排成一排,三个女生两两都不相邻,有多少种不同排法?不相邻问题对于不相邻问题,常用 “插空法”★ 某些元素不相邻排列时,可以先排其他元素,再将这些不相邻元素插入空挡,这种方法称为“插空法”;
不相邻问题插空处理的策略1、平均分组问题:n个不同元素平均分成m组,每组k个元素,则分组的方法:例1.有两本不同的书,平均分成两组有几种不同分法?
有三本不同的书,平均分成三组有几种不同分法?
有四本不同的书,平均分成两组有几种不同分法?
有六本不同的书,平均分成两组有几种不同分法?结论:n个不同元素平均分成m组,每组k个元素,则分组的方法为:一、平均分组与平均分配问题2、平均分配问题:n个不同元素平均分给m个不同对象,每个对象k个元素,则分配的方法:结论:n个不同元素平均分给m个不同对象,每个对象k个元素,则分配的方法为:结论二、非平均分组与分配问题二、非平均分组与分配问题1、非平均分组问题(2)先分成3组,分别有1、2、3本书,再分配各三个人,则有2、非平均分配问题包括两种:(1)定向的非平均分配与非平均分组的分法种数一样(2)非定向的非平均分配的分法种数三、部分平均分组与分配问题1定序问题----空位插入法例 7人排队,其中甲乙丙3人顺序一定共有多
少不同的排法解:(空位法)设想有7把椅子让除甲乙丙以外
的四人就坐共有 种方法,其余的三个
位置甲乙丙共有 种坐法,则共有 种
方法 1 重排问题----求幂策略例 把6名实习生分配到7个车间实习,共有
多少种不同的分法解:完成此事共分六步:把第一名实习生分配
到车间有 种分法.7 多排问题---直排法例7.8人排成前后两排,每排4人,其中甲乙在
前排,丁在后排,共有多少排法解:8人排前后两排,相当于8人坐8把椅子,可以
把椅子排成一排.一般地,元素分成多排的排列问题,可归结为一排考虑,再分段研究.例 10个相同的球装5个盒中,每盒至少一个,有多少装法? 元素相同问题隔板策略练 有10个运动员名额,在分给7个班,每
班至少一个,有多少种分配方案? 解:因为10个名额没有差别,把它们排成
一排。相邻名额之间形成9个空隙。在9个空档中选6个位置插个隔板,
可把名额分成7份,对应地分给7个
班级,每一种插板方法对应一种分法
共有___________种分法。 排列组合混合问题--先选后排例8.有5个不同的小球,装入4个不同的盒内,
每盒至少装一个球,共有多少不同的装
法.解:第一步从5个球中选出2个组成复合元共
有__种方法.再把5个元素(包含一个复合
元素)装入4个不同的盒内有_____种方法.根据分步计数原理装球的方法共有_____解决排列组合混合问题,先选后排是最基本
的指导思想.此法与相邻元素捆绑策略相似
吗?对于条件比较复杂的排列组合问题,不易用
公式进行运算,往往利用穷举法或画出树状
图会收到意想不到的结果练习题 同一寝室4人,每人写一张贺年卡集中起来,
然后每人各拿一张别人的贺年卡,则四张
贺年卡不同的分配方式有多少种?(9)1A 2B 3C 4D二项式定理部分 二项展开式的通项: 一般地, 展开式的二项式系数
有如下性质: (1) (2) (4)(对称性)赋值法18204. 的展开式中,第五项与第三项的二项式系
数之比为14:3,求展开式的常数项15. 展开式的二项式系数之和为128、那么展开式的项数是 ;各项系数之和为: 1、计算0.9973 的近似值(精确到0.001)0.9973= (1-0.003)3
=1?3·0.003+3·0.0032?0.0033
≈1?3·0.003
=0.991近似计算问题练习:求2.9986的近似值(精确到小数点后第三位);2.9986=(3-0.002)6
=36?6·35·0.002+15·34·0.0022?20·33·0.0023+…
≈36?6·35·0.002+15·34·0.0022=729?2.916+0.00486
≈ 726.089求:112004被10除的余数。余数与整除问题练:①5510被8除的余数.
②5710被8除的余数.求证:5555+1能被8整除; 因为5555+1=(56?1)55+1=56·M?1+1=56·M,所以5555+1能被8整除.余数与整除问题求证:42n+1+3n+2能被13整除;42n+1+3n+2=4·16n+9·3n
=4·(13+3)n+9·3n
=4·13·M+4·3n+9·3n
=4·13·M+13·3n所以42n+1+3n+2能被13整除.求值、等式与不等式证明问题⑶求证:
本
原
理组合排列排列数公式组合数公式组合数性质应
用
问
题知识结构二项式定理分类计数原理 完成一件事,有n类办法,在第1类办法中,有m1种不同的方法,在第2类办法中,有m2种不同的方法……在第n类办法中,有mn种不同的方法,则完成这件事有N=m1+m2+ ……+mn种不同的方法分步计数原理 完成一件事,需要分成n个步骤,在第1步中,有m1种不同的方法,在第2步中,有m2种不同的方法……在第n步中,有mn种不同的方法,则完成这件事有N=m1×m2× ……×mn种不同的方法两个基本原理问题1:
从甲地到乙地,可以乘火
车,也可以乘汽车,一天中,
火车有 3 班,汽车有2 班,那
么一天中,乘这些交通工具从
甲地到乙地共有多少种不同的
走法?问题2:
从甲地到乙地,要从甲地先
乘火车到丙地,再于次日从丙地
乘汽车到乙地,一天中,火车有
3班,汽车有2班,那么两天中,
从甲地到乙地共有多少种不同的
走法? 从甲地到乙地,有2类办
法,第1类办法乘火车,有3
种不同的走法,第2类办法乘
汽车,有2种不同的走法,那
么从甲地到乙地共有
3+2 = 5
种不同的走法。 从甲地到乙地,需要分成2
个步骤,第1步从甲地到丙地有
3种不同的走法,第2步从丙地
到乙地有2种不同的走法,那么
从甲地到乙地共有
3×2 = 6
种不同的走法。联系区别一完成一件事情共有n类
办法,关键词是“分类”完成一件事情,共分n个
步骤,关键词是“分步”
区别二
每类办法都能独立完成
这件事情。每一步得到的只是中间结果,
任何一步都不能能独立完成
这件事情,缺少任何一步也
不能完成这件事情,只有每
个步骤完成了,才能完成这
件事情。
分类计数原理和分步计数原理,回答的都是关于
完成一件事情的不同方法的种数的问题。
区别三各类办法是互斥的、
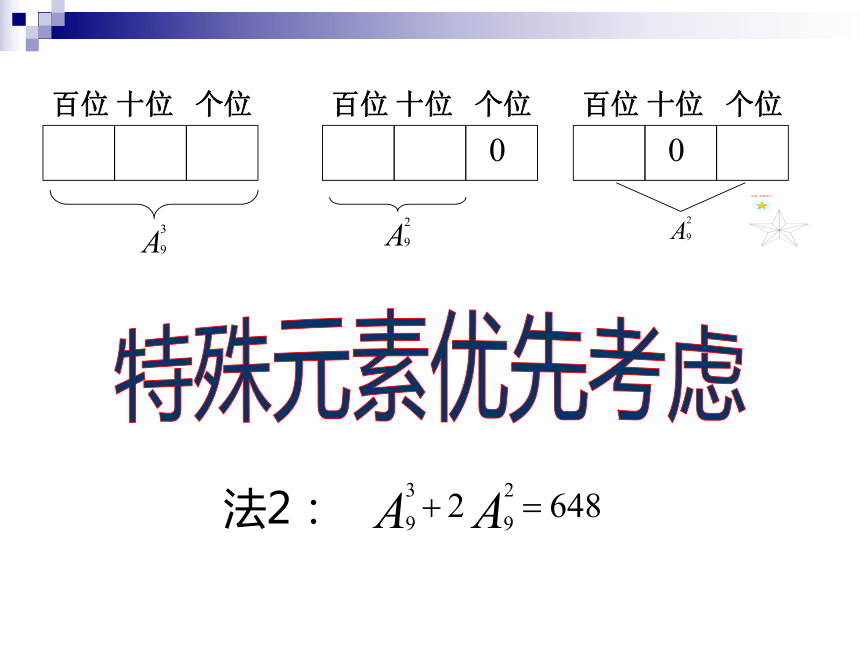
并列的、独立的各步之间是相关联的分类计数与分步计数原理的区别和联系1.某校组织学生分4个组从3处风景点中选一处去春游,则不同的春游方案的种数是( )2.某校组织学生分3个组从4处风景点中选一处去春游,则不同的春游方案的种数是( )典型例题从n个不同元素中,任取m个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.1.排列的定义:从n个不同元素中,任取m个元素,合成一组,叫做从n个不同元素中取出m个元素的一个组合.2.组合的定义:排列组合④两个组合的元素完全相同为相同组合排列数、组合数计算公式组合数的两个性质性质1性质2有特殊元素和特殊位置的排列问题例:用0到9这10个数字可以组成多少个没有重复数字的三位数? 特殊位置“百位”,特殊元素“0”特殊位置优先安排特殊元素优先考虑正难则反(间接法)相邻问题例:4男3女排成一排,三个女生排在一起,有多少种不同排法?对于相邻问题,常用“捆绑法”★ 某些元素要求必须相邻时,可以先将这些元素看作一个元素,与其他元素排列后,再考虑相邻元素的内部排列,这种方法称为“捆绑法”;
相邻问题捆绑处理的策略例:4男3女排成一排,三个女生两两都不相邻,有多少种不同排法?不相邻问题对于不相邻问题,常用 “插空法”★ 某些元素不相邻排列时,可以先排其他元素,再将这些不相邻元素插入空挡,这种方法称为“插空法”;
不相邻问题插空处理的策略1、平均分组问题:n个不同元素平均分成m组,每组k个元素,则分组的方法:例1.有两本不同的书,平均分成两组有几种不同分法?
有三本不同的书,平均分成三组有几种不同分法?
有四本不同的书,平均分成两组有几种不同分法?
有六本不同的书,平均分成两组有几种不同分法?结论:n个不同元素平均分成m组,每组k个元素,则分组的方法为:一、平均分组与平均分配问题2、平均分配问题:n个不同元素平均分给m个不同对象,每个对象k个元素,则分配的方法:结论:n个不同元素平均分给m个不同对象,每个对象k个元素,则分配的方法为:结论二、非平均分组与分配问题二、非平均分组与分配问题1、非平均分组问题(2)先分成3组,分别有1、2、3本书,再分配各三个人,则有2、非平均分配问题包括两种:(1)定向的非平均分配与非平均分组的分法种数一样(2)非定向的非平均分配的分法种数三、部分平均分组与分配问题1定序问题----空位插入法例 7人排队,其中甲乙丙3人顺序一定共有多
少不同的排法解:(空位法)设想有7把椅子让除甲乙丙以外
的四人就坐共有 种方法,其余的三个
位置甲乙丙共有 种坐法,则共有 种
方法 1 重排问题----求幂策略例 把6名实习生分配到7个车间实习,共有
多少种不同的分法解:完成此事共分六步:把第一名实习生分配
到车间有 种分法.7 多排问题---直排法例7.8人排成前后两排,每排4人,其中甲乙在
前排,丁在后排,共有多少排法解:8人排前后两排,相当于8人坐8把椅子,可以
把椅子排成一排.一般地,元素分成多排的排列问题,可归结为一排考虑,再分段研究.例 10个相同的球装5个盒中,每盒至少一个,有多少装法? 元素相同问题隔板策略练 有10个运动员名额,在分给7个班,每
班至少一个,有多少种分配方案? 解:因为10个名额没有差别,把它们排成
一排。相邻名额之间形成9个空隙。在9个空档中选6个位置插个隔板,
可把名额分成7份,对应地分给7个
班级,每一种插板方法对应一种分法
共有___________种分法。 排列组合混合问题--先选后排例8.有5个不同的小球,装入4个不同的盒内,
每盒至少装一个球,共有多少不同的装
法.解:第一步从5个球中选出2个组成复合元共
有__种方法.再把5个元素(包含一个复合
元素)装入4个不同的盒内有_____种方法.根据分步计数原理装球的方法共有_____解决排列组合混合问题,先选后排是最基本
的指导思想.此法与相邻元素捆绑策略相似
吗?对于条件比较复杂的排列组合问题,不易用
公式进行运算,往往利用穷举法或画出树状
图会收到意想不到的结果练习题 同一寝室4人,每人写一张贺年卡集中起来,
然后每人各拿一张别人的贺年卡,则四张
贺年卡不同的分配方式有多少种?(9)1A 2B 3C 4D二项式定理部分 二项展开式的通项: 一般地, 展开式的二项式系数
有如下性质: (1) (2) (4)(对称性)赋值法18204. 的展开式中,第五项与第三项的二项式系
数之比为14:3,求展开式的常数项15. 展开式的二项式系数之和为128、那么展开式的项数是 ;各项系数之和为: 1、计算0.9973 的近似值(精确到0.001)0.9973= (1-0.003)3
=1?3·0.003+3·0.0032?0.0033
≈1?3·0.003
=0.991近似计算问题练习:求2.9986的近似值(精确到小数点后第三位);2.9986=(3-0.002)6
=36?6·35·0.002+15·34·0.0022?20·33·0.0023+…
≈36?6·35·0.002+15·34·0.0022=729?2.916+0.00486
≈ 726.089求:112004被10除的余数。余数与整除问题练:①5510被8除的余数.
②5710被8除的余数.求证:5555+1能被8整除; 因为5555+1=(56?1)55+1=56·M?1+1=56·M,所以5555+1能被8整除.余数与整除问题求证:42n+1+3n+2能被13整除;42n+1+3n+2=4·16n+9·3n
=4·(13+3)n+9·3n
=4·13·M+4·3n+9·3n
=4·13·M+13·3n所以42n+1+3n+2能被13整除.求值、等式与不等式证明问题⑶求证:
