均值不等式[上学期]

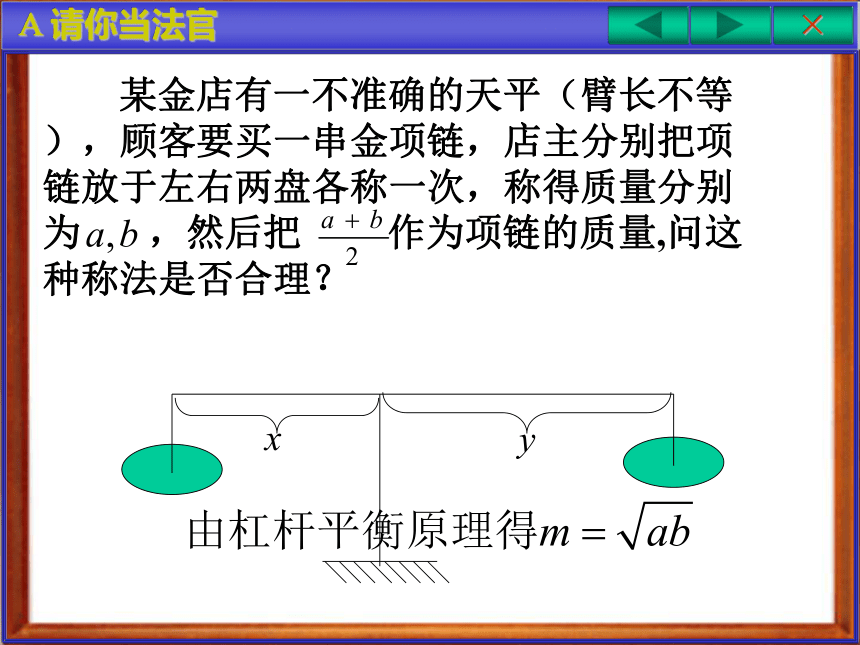
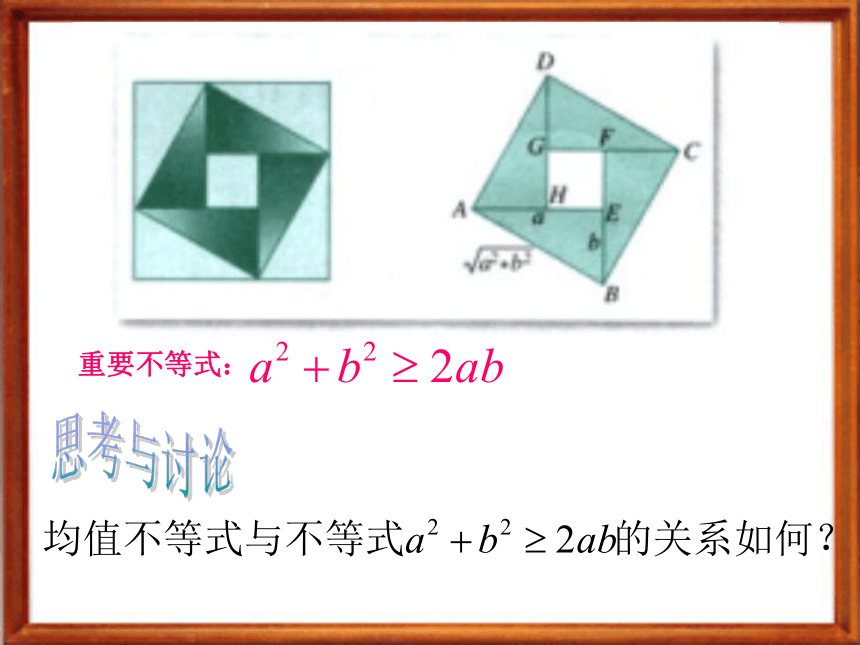
课件20张PPT。均值不等式温故而知新 A 请你当法官× 某金店有一不准确的天平（臂长不等），顾客要买一串金项链，店主分别把项链放于左右两盘各称一次，称得质量分别为 ，然后把 作为项链的质量,问这种称法是否合理？ A 要当法官先学好数学×作差法该不等式中等号何时成立？均值定理 A要当法官先学好数学ABCb·(2)几何解释: A要当法官先学好数学·结论：半径长不小于半弦长重要不等式：思考与讨论辨一辨（1）任意两个同号的数的算术平均值不小于它们的几何
平均值( )( )( )( )例1：证明：等号成立的条件：变形得：小试牛刀证明：等号成立的条件：例2：解：所以所以小试牛刀变式解：解：（1）均值不等式及其成立的条件（2）利用均值不等式求最值
（特别注意等号成立的条件）归纳总结：
均值不等式的几种特殊形式作业（1）练习B第3题
（2）习题3-2A第1，2，3题( B )析：能力提高例1： A 请你当法官证明：根据均值不等式，得即：当且仅当又赵爽（Zhao Shuang, 3世纪初） 中国数学家。东汉末至三国时代人。生平不详，约生活于公元3世纪初。字君卿，东吴人。据载，他研究过张衡的天文学著作《灵宪》和刘洪的《乾象历》，也提到过“算术”。他的主要贡献是约在222年深人研究了《周牌算经》，为该书写了序言，并作了详细注释。其中一段530余字的“勾股圆方图”注文是数学史上极有价值的文献。它记述了勾股定理的理论证明，将勾股定理表述为：“勾股各自乘，并之，为弦实。开方除之，即弦。”证明方法叙述为：“按弦图，又可以勾股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实，加差实，亦成弦实。” （见附图） 即2ab+(b-a)^2=c^2，化简便得a^2＋b^2＝c^2。其基本思想是图形经过割补后，面积不变。刘徽在注释《九章算术》时更明确地概括为出入相补原理，这是后世演段术的基础。赵爽在注文中证明了勾股形三边及其和、差关系的24个命题。例如 √(2(c-a)(c-b)) + (c-b) = a， √(2(c-a)(c-b)) + (c-a) = b， √(2(c-a)(c-b)) + (c-a) + (c-b) = c等等。他还研究了二次方程问题，得出与韦达定理类似的结果，并得到二次方程求根公式之一。此外，使用“齐同术”，在乘除时应用了这一方法，还在‘旧高图论”中给出重差术的证明。赵爽的数学思想和方法对中国古代数学体系的形成和发展有一定影 今有一台天平两臂之长略有差异，其他
均精确，有人要用它称量物体的重量，
只须将物体放在左右两个托盘中各称一
次，再将称量结果相加后除以2就是物体
的真实重量。你认为这种做法对不对？如
果不对的话，你能否找到一种用这台天平
称量物体重量的正确方法？