北师大版数学九年级上册 第四章 图形的相似4.6 利用相似三角形测高 课件(共25张PPT)
文档属性
| 名称 | 北师大版数学九年级上册 第四章 图形的相似4.6 利用相似三角形测高 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 989.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 10:05:38 | ||
图片预览







文档简介
(共25张PPT)
6 利用相似三角形测高
世界上最高的树
—— 红杉
导入新课
乐山大佛
台北101大楼
方法1:利用阳光下的影子
如图,每个小组选一名同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测量该同学的影长,另一部分同学测量同一时刻旗杆的影长,根据测量数据,你能求出旗杆的高度吗?
C
A
E
B
D
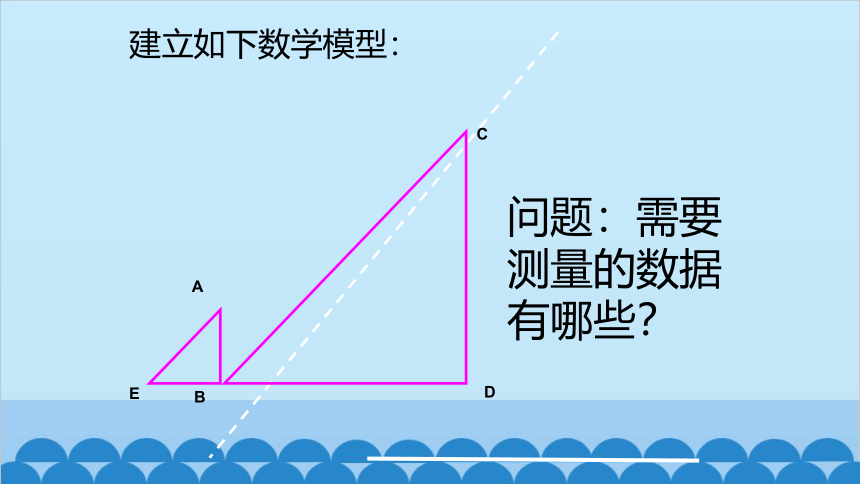
建立如下数学模型:
问题:需要测量的数据有哪些?
方法要点:
运用方法1:可以把太阳光近似地看成平行光线,计算时还要用到观测者的身高.
方法2:利用标杆
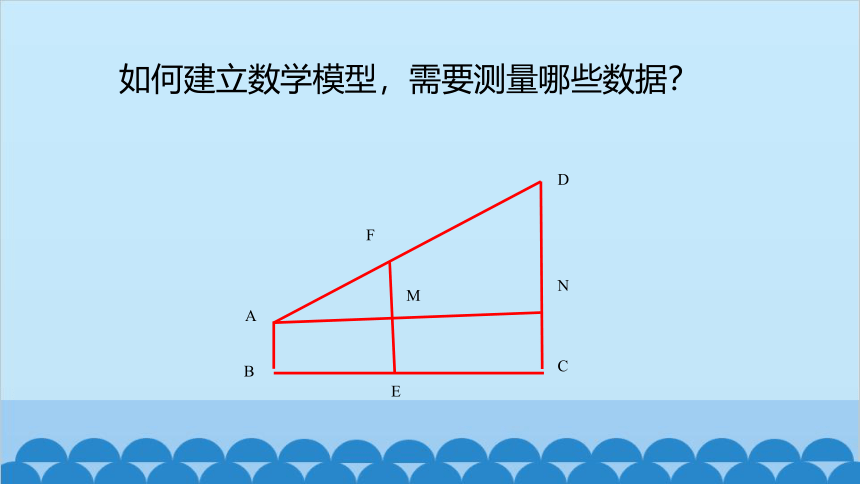
如图,每个小组选一名同学作为观测者,在观测者与旗杆之间的地面上直立一根高度适当的标杆.观测者适当调整自己所处位置,当旗杆的顶端、标杆的顶端与眼睛恰好在一条直线上时,其他同学立即测出观测者的脚到旗杆底端的距离,以及观测者的脚到标杆底端的距离,然后测出标杆的高,根据测量数据,你能求出旗杆的高度吗?说明你的理由.
如何建立数学模型,需要测量哪些数据?
A
B
C
D
E
F
M
N
方法要点:
运用方法2:观测者的眼睛必须与标杆的顶端和旗杆的顶端“三点共线”,标杆与地面要垂直,在计算时还要用到观测者的眼睛离地面的高度.
方法3:利用小镜子的反射.
如图,每个小组选一名同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记,观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合.测量所需的数据,根据所测的结果你能求出旗杆的高度吗?说明你的理由.
(1)根据题意画出___________;
(2)将题目中的已知量或已知关系转化为示意图中的_____________________;
(3)利用相似三角形建立线段之间的关系,求出__________;
(4)写出___________.
示意图
已知线段、已知角
未知量
答案
利用三角形相似解决实际问题的一般步骤:
归纳总结
例1:如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
解析:人、树、标杆是相互平行的,添加辅助线,过点A作AN∥BD交ID于N,交EF于M,则可得△AEM∽△ACN.
A
E
C
D
F
B
N
A
E
C
D
F
B
N
解:过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°,
∴AB∥EF∥CD, ∴∠EMA=∠CNA.
∵∠EAM=∠CAN,
∴△AEM∽△ACN ,
∴ .
∵AB=1.6m , EF=2m , BD=27m , FD=24m ,
∴ , ∴CN=3.6(m),
∴CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
例2:为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
解:∵∠1=∠2,∠DCE=∠BAE=90°,
∴△DCE∽△BAE.
∴ ,
解得 BA=18.75(m).
因此,树高约为18.75m.
D
B
A
C
E
2
1
1.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米 B.12米
C.15米
D.22.5米
A
2.如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
A.4.8m B.6.4m
C.8 m D.10 m
C
3.如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为 .
1.5米
4. 铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高______m.
O
B
D
C
A
┏
┛
1m
16m
0.5m
?
8
5.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为______ 米.
4
【拓展题】如图,数学兴趣小组的小颖想测量教学楼前一棵树的树高,她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是__________.
E
4.45m
【拓展题】如图,数学兴趣小组的小颖想测量教学楼前一棵树的树高,她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是__________.
E
【拓展题】如图,数学兴趣小组的小颖想测量教学楼前一棵树的树高,她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是__________.
E
利用三角形相似测高的模型:
相似三角形的应用主要有两个方面:
(1) 测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2) 测距
小 结
祝您学习进步!
快乐成长!
6 利用相似三角形测高
世界上最高的树
—— 红杉
导入新课
乐山大佛
台北101大楼
方法1:利用阳光下的影子
如图,每个小组选一名同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测量该同学的影长,另一部分同学测量同一时刻旗杆的影长,根据测量数据,你能求出旗杆的高度吗?
C
A
E
B
D
建立如下数学模型:
问题:需要测量的数据有哪些?
方法要点:
运用方法1:可以把太阳光近似地看成平行光线,计算时还要用到观测者的身高.
方法2:利用标杆
如图,每个小组选一名同学作为观测者,在观测者与旗杆之间的地面上直立一根高度适当的标杆.观测者适当调整自己所处位置,当旗杆的顶端、标杆的顶端与眼睛恰好在一条直线上时,其他同学立即测出观测者的脚到旗杆底端的距离,以及观测者的脚到标杆底端的距离,然后测出标杆的高,根据测量数据,你能求出旗杆的高度吗?说明你的理由.
如何建立数学模型,需要测量哪些数据?
A
B
C
D
E
F
M
N
方法要点:
运用方法2:观测者的眼睛必须与标杆的顶端和旗杆的顶端“三点共线”,标杆与地面要垂直,在计算时还要用到观测者的眼睛离地面的高度.
方法3:利用小镜子的反射.
如图,每个小组选一名同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记,观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合.测量所需的数据,根据所测的结果你能求出旗杆的高度吗?说明你的理由.
(1)根据题意画出___________;
(2)将题目中的已知量或已知关系转化为示意图中的_____________________;
(3)利用相似三角形建立线段之间的关系,求出__________;
(4)写出___________.
示意图
已知线段、已知角
未知量
答案
利用三角形相似解决实际问题的一般步骤:
归纳总结
例1:如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
解析:人、树、标杆是相互平行的,添加辅助线,过点A作AN∥BD交ID于N,交EF于M,则可得△AEM∽△ACN.
A
E
C
D
F
B
N
A
E
C
D
F
B
N
解:过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°,
∴AB∥EF∥CD, ∴∠EMA=∠CNA.
∵∠EAM=∠CAN,
∴△AEM∽△ACN ,
∴ .
∵AB=1.6m , EF=2m , BD=27m , FD=24m ,
∴ , ∴CN=3.6(m),
∴CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
例2:为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
解:∵∠1=∠2,∠DCE=∠BAE=90°,
∴△DCE∽△BAE.
∴ ,
解得 BA=18.75(m).
因此,树高约为18.75m.
D
B
A
C
E
2
1
1.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米 B.12米
C.15米
D.22.5米
A
2.如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
A.4.8m B.6.4m
C.8 m D.10 m
C
3.如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为 .
1.5米
4. 铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高______m.
O
B
D
C
A
┏
┛
1m
16m
0.5m
?
8
5.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为______ 米.
4
【拓展题】如图,数学兴趣小组的小颖想测量教学楼前一棵树的树高,她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是__________.
E
4.45m
【拓展题】如图,数学兴趣小组的小颖想测量教学楼前一棵树的树高,她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是__________.
E
【拓展题】如图,数学兴趣小组的小颖想测量教学楼前一棵树的树高,她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是__________.
E
利用三角形相似测高的模型:
相似三角形的应用主要有两个方面:
(1) 测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2) 测距
小 结
祝您学习进步!
快乐成长!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
