15.3 等腰三角形 (2) 课件(共25张PPT)
文档属性
| 名称 | 15.3 等腰三角形 (2) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 945.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 12:11:14 | ||
图片预览





文档简介
(共25张PPT)
沪科版 八年级上册
15. 3 等腰三角形(2)
1.掌握等腰三角形两底角相等的性质;
2.掌握等腰三角形顶角平分线与底边上的高,底边上的中线三线合一的性质.
教学重点:
运用等腰三角形性质解题.
教学难点:
运用等腰三角形的性质解题.
教学目标:
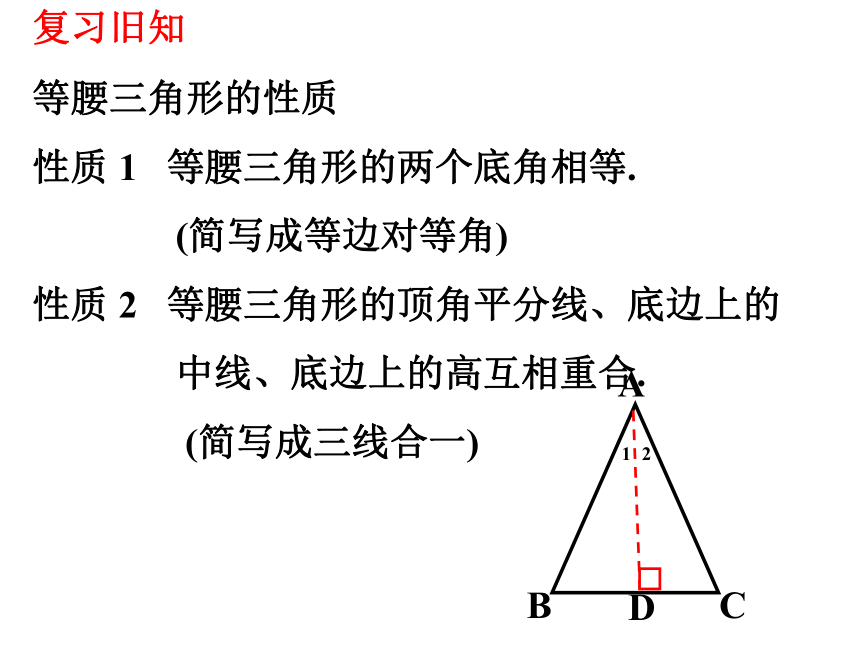
等腰三角形的性质
性质 1 等腰三角形的两个底角相等.
(简写成等边对等角)
性质 2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合.
(简写成三线合一)
A
B
C
1
2
D
复习旧知
1.下列说法正确的是( ).
A.等腰三角形的高、中线、角平分线互相重合
B.顶角相等的两个等腰三角形全等
C.等腰三角形的两个底角相等
D.等腰三角形一边不可以是另一边的二倍
A
2.如果等腰三角形两边长是7 cm和5 cm,
那么它的周长是( ).
A.12 cm B.17 cm
C.19 cm D.17 cm或19 cm
3.如果等腰三角形两边长是6 cm和13 cm,
那么它的周长是( ).
A.19 cm B.25cm
C.32 cm D.25 cm或32 cm
D
C
要求
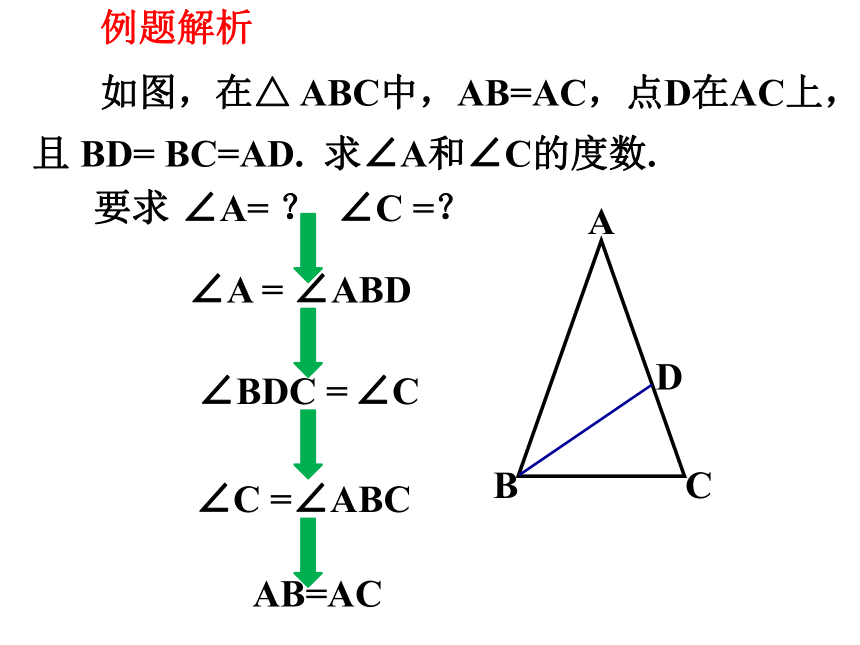
如图,在△ ABC中,AB=AC,点D在AC上,
且 BD= BC=AD.
求∠A和∠C的度数.
AB=AC
∠C =∠ABC
∠A = ∠ABD
∠BDC = ∠C
∠A= ?
∠C =?
A
B
C
D
例题解析
解:
如图,在△ ABC中,AB=AC,点D在AC上,
且 BD= BC=AD.
∴ ∠ABC=∠C,
求∠A和∠C的度数.
∵ AB=AC,
BD=BC,
∠C=∠BDC ,
BD=AD,
∠A=∠ABD.
∵∠BDC 是△ ABD的外角,
∴ ∠BDC =
∠A +∠ABD
= 2∠A.
∴ ∠ABC=∠C
= 2∠A.
∵∠A+∠ABC +∠C=180°,
∴∠A+ 2∠A+2∠A=180°,
∴ ∠A= 36°,
∴ ∠C =72°.
A
B
C
D
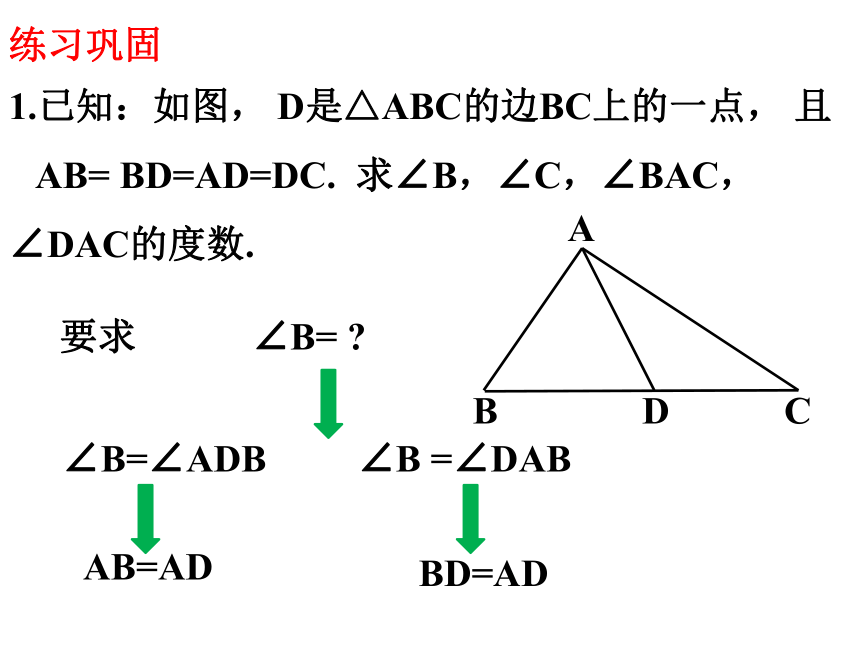
1.已知:如图, D是△ABC的边BC上的一点, 且
AB= BD=AD=DC. 求∠B,∠C,∠BAC,
∠DAC的度数.
A
B
C
D
练习巩固
∠B=∠ADB
AB=AD
BD=AD
∠B =∠DAB
∠B=
要求
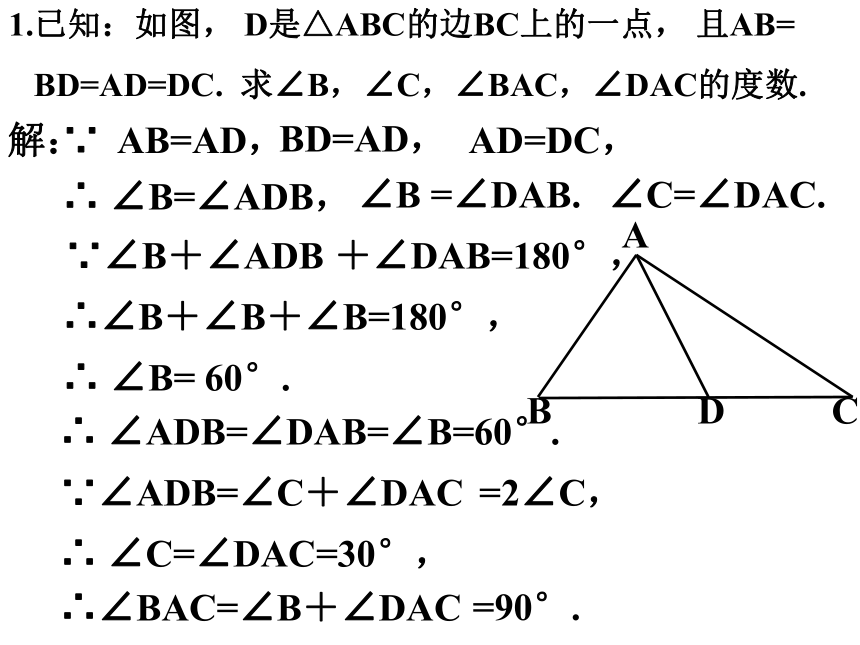
1.已知:如图, D是△ABC的边BC上的一点, 且AB=
BD=AD=DC. 求∠B,∠C,∠BAC,∠DAC的度数.
A
B
C
D
解:
∴ ∠B=∠ADB,
∵ AB=AD,
BD=AD,
∠B =∠DAB.
∵∠B+∠ADB +∠DAB=180°,
∴∠B+∠B+∠B=180°,
∴ ∠B= 60°.
AD=DC,
∠C=∠DAC.
∵∠ADB=∠C+∠DAC
∴ ∠ADB=∠DAB=∠B=60°.
=2∠C,
∴ ∠C=∠DAC=30°,
∴∠BAC=∠B+∠DAC
=90°.
求证:斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图,在Rt△ABCRt△A B C 中,∠C=∠C = 90°,AB=A B ,AC=A C .
求证:Rt△ABC≌ Rt△A B C
∟
B
C
A
∟
B
C
A
学习新知
已知:如图,在Rt△ABCRt△A B C 中,∠C=∠C = 90°,AB=A B ,AC=A C .
求证:Rt△ABC≌ Rt△A B C
∟
B
C
A
∟
B
C
A
在平面内移动Rt△A B C ,使点A 和点A、C 点和点C重合,点B和点B 在AC的两侧.
证明:
∟
B
(C )
A
∟
B
C
A
在平面内移动Rt△A B C ,使点A 和点A、C 点和点C重合,点B和点B 在AC的两侧.
证明:
∵∠BCB =90°+90°=180°,
∴ B,C,B 三点在一条直线上,
在△ABB 中,
∵AB=A B ,
∴ ∠B =∠B ,
在Rt△ABC和Rt△A B C 中,
AB=A B
Rt△ABC≌ Rt△A B C
∠B =∠B
∠ACB =∠A C B
(AAS)
2.已知:如图,AB=AC,AD=AE. 求证:BD=CE.
方法一:
证△ ABD≌ △ ACE
A
B
C
D
E
证明:
∵AB=AC,
∴∠B=∠C.
∵AD=AE,
∴∠ADE=∠AED,
AB=AC ( 已知 )
∠B= ∠C
∴ △ABD ≌ △ACE
∴ BD=CE.
在△ABD和△ACE中,
(AAS).
∴∠ADB=∠AEC.
∠ADB=∠AEC
练习巩固
2.已知:如图,AB=AC,AD=AE. 求证:BD=CE.
方法二:
证△ ABE≌ △ ACD
A
B
C
D
E
证明:
∵AB=AC,
∴∠B=∠C.
∵AD=AE,
∴∠ADC=∠AEB,
AB=AC ( 已知 ),
∠B= ∠C
∴ △ABD ≌ △ACE
∴ BE=CD.
在△ABE和△ACD中,
(AAS).
∠AEB=∠ADC
∴ BE-DE=CD-DE.
∴ BD=CE.
2.已知:如图,AB=AC,AD=AE. 求证:BD=CE.
方法三:
过A作AF⊥BC于F
A
B
C
D
E
F
证明:
AF⊥BC,
∵AB=AC,
∴BF=CF.
AF⊥DE,
∵AD=AE,
∴DF=EF.
∴ BF-DF=CF-EF.
∴ BD=CE.
过A作AF⊥BC于F
2.已知:如图,AB=AC,AD=AE. 求证:BD=CE.
A
B
C
D
E
证明:
∵AB=AC,
∴∠B=∠C.
AB=AC
∠B=∠C
∴ △ABD ≌ △ACE
在△ABE和△ACD中,
AD=AE
∴ BD=CE.
噉都得?
3.已知:如图, ∠AOB=15°, 并且
OA=AB=BC=CD. 求∠1的度数.
1
15°
O
A
B
C
D
解:
∵OA=AB,
∴∠AOB=∠ABO=15°.
∴∠BAC=∠AOB+∠ABO
=30°,
∵AB=BC,
∴∠BAC=∠BCA=30°.
∴∠CBD=∠AOB+∠BCA
=45°,
∵BC=BD,
∴∠CBD=∠D=45°.
∴∠1=∠AOB+∠D
=60°.
4.已知:如图,AB=AC,AB的垂直平分线ED交
AC于点D, ∠A=40°.求∠DBC的度数.
D
A
B
C
E
解:
∵AB=AC,
∴∠ABC=∠C.
∵ ∠A=40°,
∴∠ABC
=70°
= ×(180°-40°)
1
2
∵点D在AB的垂直平分线上,
∴DA=DB,
∴∠DBA=∠A
=40°,
∴∠DBC=∠ABC-∠ABD
=70°-40°
=30°.
课堂小结
1.我们学习了等腰三角形哪些性质?
2.运用等腰三角形的性质解题时要注意什么?
1. 已知等腰三角形的一个内角为80°,则另两个角的度数是 ( ).
A.50°,50° B.80°,20°
C.50°,50°或80°,20° D.以上都不对
2. 已知等腰三角形的一个内角为110°,则另
两个角的度数是( ).
A.110°,25° B.35°,35°
C.110°,35°或35°,35° D.以上都不对
C
B
巩固提高
4.若等腰三角形的周长为26cm,一边为11cm,
则腰长为( ).
A:11cm B:7.5cm
C:11cm或7.5cm D: 以上都不对
3.如图:∠EAF=15°,AB=BC=CD=DE=EF,
则∠DEF等于( ).
A.90° B. 75°
C.70° D. 60°
15°
E
A
B
C
D
F
D
C
5.如图,△ABC中,∠A=90°,AB=AC,D为BC
的中点,E、F分别是AB,AC上的点,且BE=AF.
求证: DE=DF.
B
A
D
E
C
F
证明:
连接AD,
∴ ∠B =∠C=45°.
∵∠A=90°,AB=AC,
∵D为BC 的中点,
∴ ∠DAF =45°,
AD=CD=BD.
∵BE=AF,
∴ △BDE ≌△ADF
∴ DE=DF.
∴ ∠B =∠DAF.
今天作业
课本P140页第7、11题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
15. 3 等腰三角形(2)
1.掌握等腰三角形两底角相等的性质;
2.掌握等腰三角形顶角平分线与底边上的高,底边上的中线三线合一的性质.
教学重点:
运用等腰三角形性质解题.
教学难点:
运用等腰三角形的性质解题.
教学目标:
等腰三角形的性质
性质 1 等腰三角形的两个底角相等.
(简写成等边对等角)
性质 2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合.
(简写成三线合一)
A
B
C
1
2
D
复习旧知
1.下列说法正确的是( ).
A.等腰三角形的高、中线、角平分线互相重合
B.顶角相等的两个等腰三角形全等
C.等腰三角形的两个底角相等
D.等腰三角形一边不可以是另一边的二倍
A
2.如果等腰三角形两边长是7 cm和5 cm,
那么它的周长是( ).
A.12 cm B.17 cm
C.19 cm D.17 cm或19 cm
3.如果等腰三角形两边长是6 cm和13 cm,
那么它的周长是( ).
A.19 cm B.25cm
C.32 cm D.25 cm或32 cm
D
C
要求
如图,在△ ABC中,AB=AC,点D在AC上,
且 BD= BC=AD.
求∠A和∠C的度数.
AB=AC
∠C =∠ABC
∠A = ∠ABD
∠BDC = ∠C
∠A= ?
∠C =?
A
B
C
D
例题解析
解:
如图,在△ ABC中,AB=AC,点D在AC上,
且 BD= BC=AD.
∴ ∠ABC=∠C,
求∠A和∠C的度数.
∵ AB=AC,
BD=BC,
∠C=∠BDC ,
BD=AD,
∠A=∠ABD.
∵∠BDC 是△ ABD的外角,
∴ ∠BDC =
∠A +∠ABD
= 2∠A.
∴ ∠ABC=∠C
= 2∠A.
∵∠A+∠ABC +∠C=180°,
∴∠A+ 2∠A+2∠A=180°,
∴ ∠A= 36°,
∴ ∠C =72°.
A
B
C
D
1.已知:如图, D是△ABC的边BC上的一点, 且
AB= BD=AD=DC. 求∠B,∠C,∠BAC,
∠DAC的度数.
A
B
C
D
练习巩固
∠B=∠ADB
AB=AD
BD=AD
∠B =∠DAB
∠B=
要求
1.已知:如图, D是△ABC的边BC上的一点, 且AB=
BD=AD=DC. 求∠B,∠C,∠BAC,∠DAC的度数.
A
B
C
D
解:
∴ ∠B=∠ADB,
∵ AB=AD,
BD=AD,
∠B =∠DAB.
∵∠B+∠ADB +∠DAB=180°,
∴∠B+∠B+∠B=180°,
∴ ∠B= 60°.
AD=DC,
∠C=∠DAC.
∵∠ADB=∠C+∠DAC
∴ ∠ADB=∠DAB=∠B=60°.
=2∠C,
∴ ∠C=∠DAC=30°,
∴∠BAC=∠B+∠DAC
=90°.
求证:斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图,在Rt△ABCRt△A B C 中,∠C=∠C = 90°,AB=A B ,AC=A C .
求证:Rt△ABC≌ Rt△A B C
∟
B
C
A
∟
B
C
A
学习新知
已知:如图,在Rt△ABCRt△A B C 中,∠C=∠C = 90°,AB=A B ,AC=A C .
求证:Rt△ABC≌ Rt△A B C
∟
B
C
A
∟
B
C
A
在平面内移动Rt△A B C ,使点A 和点A、C 点和点C重合,点B和点B 在AC的两侧.
证明:
∟
B
(C )
A
∟
B
C
A
在平面内移动Rt△A B C ,使点A 和点A、C 点和点C重合,点B和点B 在AC的两侧.
证明:
∵∠BCB =90°+90°=180°,
∴ B,C,B 三点在一条直线上,
在△ABB 中,
∵AB=A B ,
∴ ∠B =∠B ,
在Rt△ABC和Rt△A B C 中,
AB=A B
Rt△ABC≌ Rt△A B C
∠B =∠B
∠ACB =∠A C B
(AAS)
2.已知:如图,AB=AC,AD=AE. 求证:BD=CE.
方法一:
证△ ABD≌ △ ACE
A
B
C
D
E
证明:
∵AB=AC,
∴∠B=∠C.
∵AD=AE,
∴∠ADE=∠AED,
AB=AC ( 已知 )
∠B= ∠C
∴ △ABD ≌ △ACE
∴ BD=CE.
在△ABD和△ACE中,
(AAS).
∴∠ADB=∠AEC.
∠ADB=∠AEC
练习巩固
2.已知:如图,AB=AC,AD=AE. 求证:BD=CE.
方法二:
证△ ABE≌ △ ACD
A
B
C
D
E
证明:
∵AB=AC,
∴∠B=∠C.
∵AD=AE,
∴∠ADC=∠AEB,
AB=AC ( 已知 ),
∠B= ∠C
∴ △ABD ≌ △ACE
∴ BE=CD.
在△ABE和△ACD中,
(AAS).
∠AEB=∠ADC
∴ BE-DE=CD-DE.
∴ BD=CE.
2.已知:如图,AB=AC,AD=AE. 求证:BD=CE.
方法三:
过A作AF⊥BC于F
A
B
C
D
E
F
证明:
AF⊥BC,
∵AB=AC,
∴BF=CF.
AF⊥DE,
∵AD=AE,
∴DF=EF.
∴ BF-DF=CF-EF.
∴ BD=CE.
过A作AF⊥BC于F
2.已知:如图,AB=AC,AD=AE. 求证:BD=CE.
A
B
C
D
E
证明:
∵AB=AC,
∴∠B=∠C.
AB=AC
∠B=∠C
∴ △ABD ≌ △ACE
在△ABE和△ACD中,
AD=AE
∴ BD=CE.
噉都得?
3.已知:如图, ∠AOB=15°, 并且
OA=AB=BC=CD. 求∠1的度数.
1
15°
O
A
B
C
D
解:
∵OA=AB,
∴∠AOB=∠ABO=15°.
∴∠BAC=∠AOB+∠ABO
=30°,
∵AB=BC,
∴∠BAC=∠BCA=30°.
∴∠CBD=∠AOB+∠BCA
=45°,
∵BC=BD,
∴∠CBD=∠D=45°.
∴∠1=∠AOB+∠D
=60°.
4.已知:如图,AB=AC,AB的垂直平分线ED交
AC于点D, ∠A=40°.求∠DBC的度数.
D
A
B
C
E
解:
∵AB=AC,
∴∠ABC=∠C.
∵ ∠A=40°,
∴∠ABC
=70°
= ×(180°-40°)
1
2
∵点D在AB的垂直平分线上,
∴DA=DB,
∴∠DBA=∠A
=40°,
∴∠DBC=∠ABC-∠ABD
=70°-40°
=30°.
课堂小结
1.我们学习了等腰三角形哪些性质?
2.运用等腰三角形的性质解题时要注意什么?
1. 已知等腰三角形的一个内角为80°,则另两个角的度数是 ( ).
A.50°,50° B.80°,20°
C.50°,50°或80°,20° D.以上都不对
2. 已知等腰三角形的一个内角为110°,则另
两个角的度数是( ).
A.110°,25° B.35°,35°
C.110°,35°或35°,35° D.以上都不对
C
B
巩固提高
4.若等腰三角形的周长为26cm,一边为11cm,
则腰长为( ).
A:11cm B:7.5cm
C:11cm或7.5cm D: 以上都不对
3.如图:∠EAF=15°,AB=BC=CD=DE=EF,
则∠DEF等于( ).
A.90° B. 75°
C.70° D. 60°
15°
E
A
B
C
D
F
D
C
5.如图,△ABC中,∠A=90°,AB=AC,D为BC
的中点,E、F分别是AB,AC上的点,且BE=AF.
求证: DE=DF.
B
A
D
E
C
F
证明:
连接AD,
∴ ∠B =∠C=45°.
∵∠A=90°,AB=AC,
∵D为BC 的中点,
∴ ∠DAF =45°,
AD=CD=BD.
∵BE=AF,
∴ △BDE ≌△ADF
∴ DE=DF.
∴ ∠B =∠DAF.
今天作业
课本P140页第7、11题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
