15.3 等腰三角形 (1) 课件(共25张PPT)
文档属性
| 名称 | 15.3 等腰三角形 (1) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 12:14:00 | ||
图片预览



文档简介
(共25张PPT)
沪科版 八年级上册
15. 3 等腰三角形(1)
1.掌握等腰三角形两底角相等的性质;
2.掌握等腰三角形顶角平分线与底边上的高,底边上的中线三线合一的性质.
教学重点:
运用等腰三角形性质解题.
教学难点:
等腰三角形性质的证明.
教学目标:
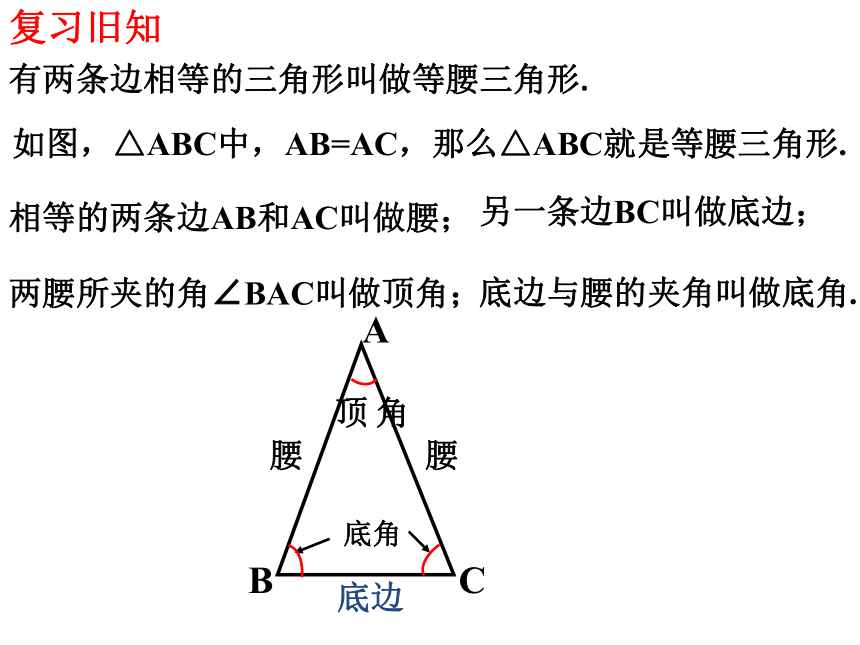
有两条边相等的三角形叫做等腰三角形.
A
B
C
腰
腰
底边
底角
角顶
相等的两条边AB和AC叫做腰;
如图,△ABC中,AB=AC,那么△ABC就是等腰三角形.
另一条边BC叫做底边;
两腰所夹的角∠BAC叫做顶角;
底边与腰的夹角叫做底角.
复习旧知
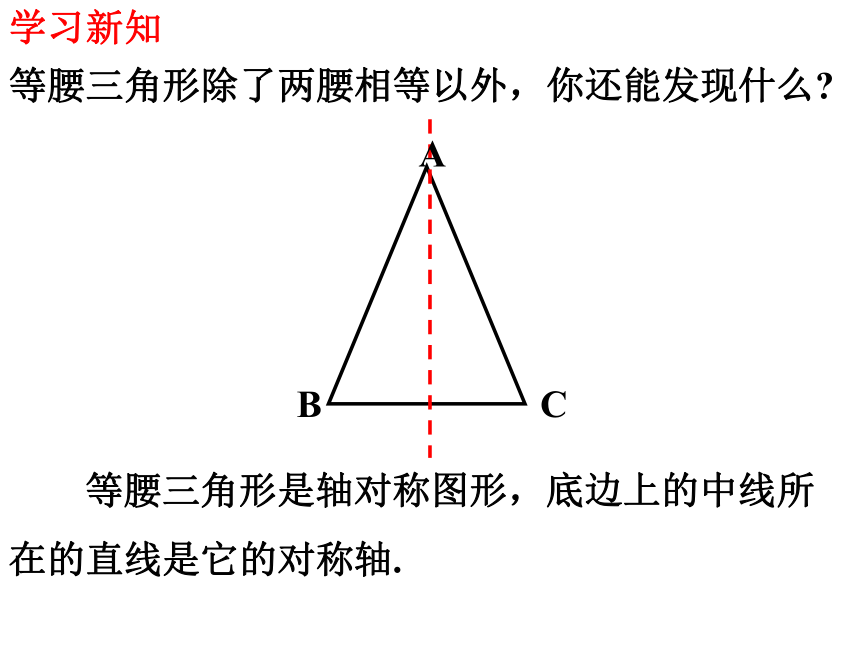
等腰三角形除了两腰相等以外,你还能发现什么
A
B
C
等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴.
学习新知
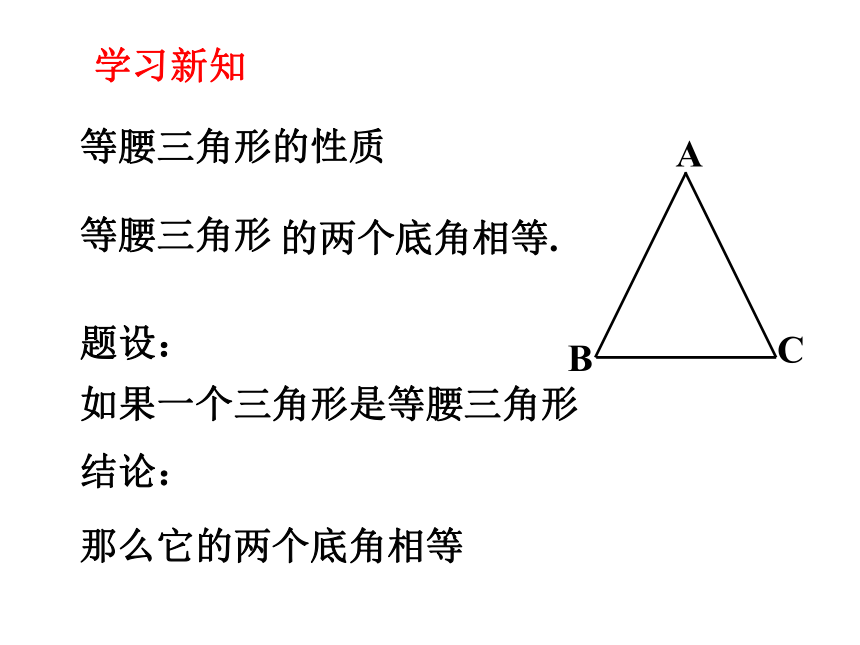
等腰三角形的性质
A
B
C
的两个底角相等.
等腰三角形
题设:
如果一个三角形是等腰三角形
结论:
那么它的两个底角相等
学习新知
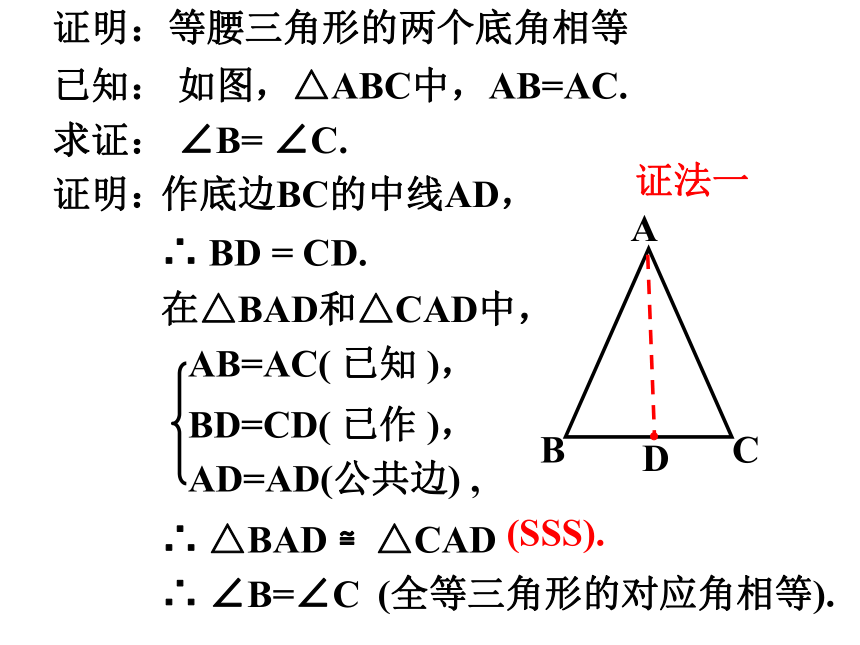
证明:
作底边BC的中线AD,
AB=AC( 已知 ),
BD=CD( 已作 ),
AD=AD(公共边) ,
∴ △BAD ≌△CAD
∴ ∠B=∠C
已知: 如图,△ABC中,AB=AC.
A
B
C
证明:等腰三角形的两个底角相等
D
求证: ∠B= ∠C.
∴ BD = CD.
在△BAD和△CAD中,
(SSS).
(全等三角形的对应角相等).
证法一
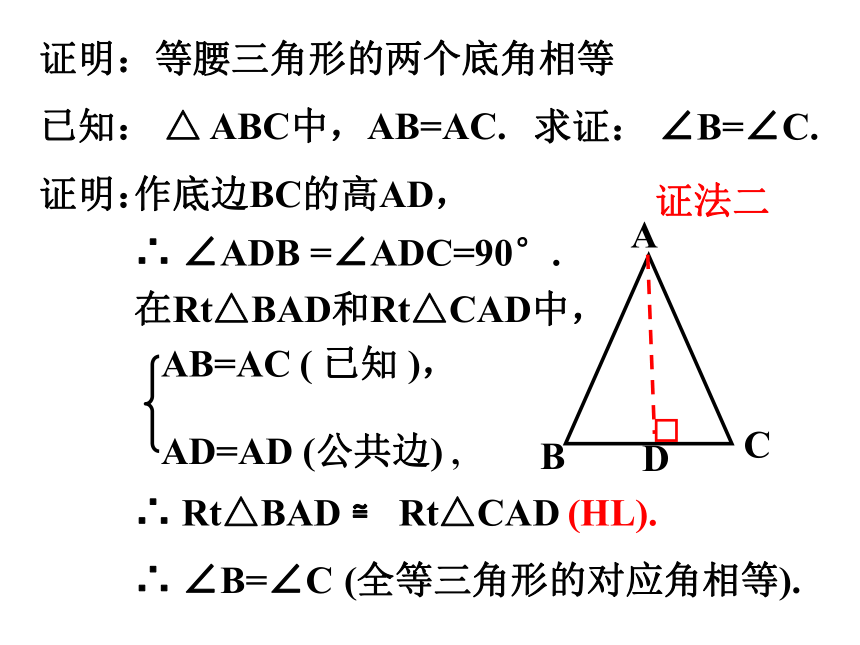
证明:
作底边BC的高AD,
AB=AC ( 已知 ),
AD=AD (公共边) ,
∴ Rt△BAD ≌ Rt△CAD
∴ ∠B=∠C
已知: △ ABC中,AB=AC.
A
B
C
证明:等腰三角形的两个底角相等
D
求证: ∠B=∠C.
∴ ∠ADB =∠ADC=90°.
在Rt△BAD和Rt△CAD中,
(HL).
(全等三角形的对应角相等).
证法二
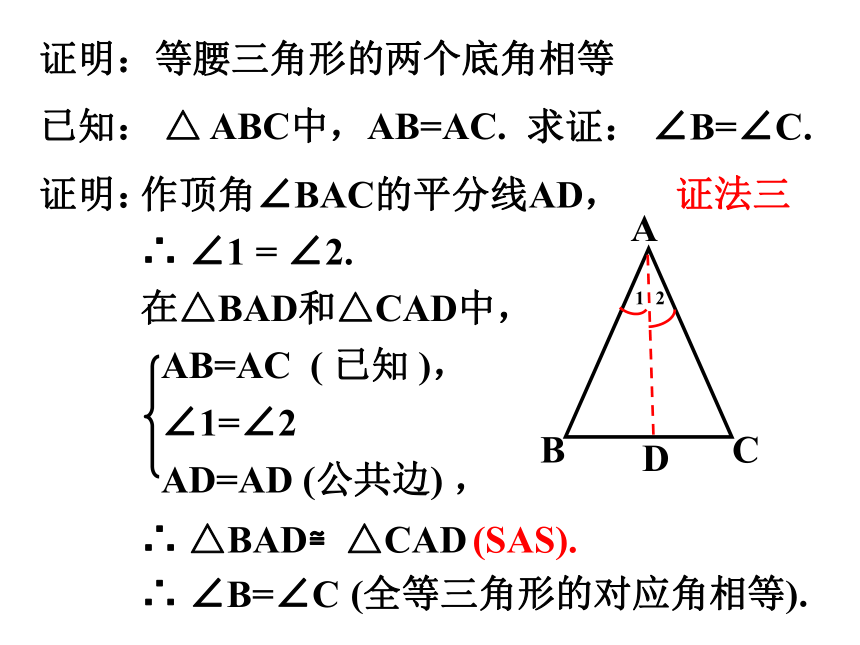
证明:
作顶角∠BAC的平分线AD,
AB=AC ( 已知 ),
∠1=∠2
AD=AD (公共边) ,
∴ △BAD≌△CAD
∴ ∠B=∠C
已知: △ ABC中,AB=AC.
A
B
C
1
2
证明:等腰三角形的两个底角相等
D
求证: ∠B=∠C.
∴ ∠1 = ∠2.
在△BAD和△CAD中,
(SAS).
(全等三角形的对应角相等).
证法三
等腰三角形的性质
A
B
C
应用格式:
在△ABC中
∵ AB=AC
∴ ∠B=∠C
的两个底角相等.
等腰三角形
(可以简称:等边对等角)
(等边对等角)
证明:
过点A作BC的垂直平分线AD.
已知: △ ABC中,AB=AC.
A
B
C
1
2
D
求证: ∠B= ∠C.
×
过点A作BC的垂线AD.
过点A作∠BAC的平分线AD.
过点A作BC的中线AD.
√
√
√
注意作图语言的规范表述
证明:
作顶角∠BAC的平分线AD,
AB=AC ( 已知 ),
∠ 1= ∠ 2
AD=AD (公共边) ,
∴ △BAD ≌ △CAD
∴ BD=CD,
A
B
C
1
2
D
∴ ∠1 = ∠2.
在△BAD和△CAD中,
(SAS).
∠ADB=∠ADC.
∵∠ADB +∠ADC=180°,
∴∠ADB=90°.
∴AD垂直平分BC.
∴ ∠B=∠C
还可推出什么结论?
等腰三角形顶角平分线垂直平分底边.
等腰三角形的性质2
等腰三角形顶角平分线垂直平分底边.
等腰三角形的顶角平分线、底边上的中线、 底边上的高互相重合.
A
B
C
1
2
D
(简写成三线合一)
学习新知
等腰三角形的性质
性质 1 等腰三角形的两个底角相等.
(简写成等边对等角)
性质 2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合.
(简写成三线合一)
A
B
C
1
2
D
“三线合一”
A
B
C
D
(1) 在△ABC中, AB=AC,
AD⊥BC,
∴____⊥____ ,∠_____ =∠_____.
∴____ ⊥____ ,_____ =_____.
∴∠_____ = ∠_____,____= ____.
(2) 在△ABC中, AB=AC,
(3) 在△ABC中, AB=AC,
∠BAD =∠CAD ,
BD=DC,
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
练习巩固
例1 已知:如图,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.
A
B
C
D
E
要求:
AB=AC
∠B=∠C
∠DAB=∠B
∠EAC=∠C
∠DAE
∠DAB =? ∠EAC=?
例题解析
例1 已知:如图,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.
A
B
C
D
E
解:
∵AB=AC,
∴∠B=∠C.
∵∠BAC=120°,
∴∠B=∠C
∵BD=AD,
CE=AE,
∴∠DAB=∠B=30°,
∠EAC=∠C=30°.
∴∠DAE
=∠BAC-∠DAB-∠EAC
=120°-30°-30°
=60°
=30°
= ×(180°-120°)
1
2
1.如图,△ABC中, AB=AC,AD=BD, DE⊥AB
于点E,若BC=10 ,且△BDC的周长为24,求AE
的长.
巩固提高
解:
∵BC=10,
∴BD+CD=14.
B
A
D
E
C
△BDC的周长为24,
∵AD=BD,
∴AD+CD=AC=14.
∵AB=AC,
∴AB=14.
∵AD=BD,DE⊥AB,
∴AE= AB=7.
1
2
2.如图,△ABC中, AB=AC,点D在且△ABC外,
CD⊥AD于D,CD= BC,求证: ∠ACD=∠B.
1
2
B
A
D
C
证明:
E
过点A作AE⊥BC于E,
AB=AC
BE=CD
∴ Rt△ABE ≌ Rt△ACD
∴ ∠ACD=∠B.
∴ ∠AEB =90°.
在Rt△ABE和Rt△ACD中,
(HL).
∴ ∠AEB =∠ADC=90°.
∴ ∠ADC=90°.
∵CD⊥AD,
∵AB=AC,
∴BE= BC.
1
2
∵CD= BC,
∴BE=CD
1
2
课堂小结
1.我们学习了等腰三角形哪些性质?
2.运用等腰三角形的性质解题时要注意什么?
1.如图,在△ABC中,AB=AC,BD平分∠ABC,
BD=BE,∠A=84°,则∠DEC= .
B
A
D
E
C
巩固提高
114°
2.如图,CE平分∠ACB,且CE⊥BD,DA=DB,
AC=18,△CDB的周长为28,则BE的长为 .
B
C
D
E
A
5
3.如图,在等腰△ABC中,∠ABC=90°,D为
AC边上中点,过D点作DE⊥DF,交AB于E,
交BC于F,若AE=4,FC=3,则△ABC的面积
为 .
B
A
D
E
C
F
49
2
△ADE ≌△BDF
△BDE ≌△CDF
提示:连接BD
今天作业
课本P139页第1、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
15. 3 等腰三角形(1)
1.掌握等腰三角形两底角相等的性质;
2.掌握等腰三角形顶角平分线与底边上的高,底边上的中线三线合一的性质.
教学重点:
运用等腰三角形性质解题.
教学难点:
等腰三角形性质的证明.
教学目标:
有两条边相等的三角形叫做等腰三角形.
A
B
C
腰
腰
底边
底角
角顶
相等的两条边AB和AC叫做腰;
如图,△ABC中,AB=AC,那么△ABC就是等腰三角形.
另一条边BC叫做底边;
两腰所夹的角∠BAC叫做顶角;
底边与腰的夹角叫做底角.
复习旧知
等腰三角形除了两腰相等以外,你还能发现什么
A
B
C
等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴.
学习新知
等腰三角形的性质
A
B
C
的两个底角相等.
等腰三角形
题设:
如果一个三角形是等腰三角形
结论:
那么它的两个底角相等
学习新知
证明:
作底边BC的中线AD,
AB=AC( 已知 ),
BD=CD( 已作 ),
AD=AD(公共边) ,
∴ △BAD ≌△CAD
∴ ∠B=∠C
已知: 如图,△ABC中,AB=AC.
A
B
C
证明:等腰三角形的两个底角相等
D
求证: ∠B= ∠C.
∴ BD = CD.
在△BAD和△CAD中,
(SSS).
(全等三角形的对应角相等).
证法一
证明:
作底边BC的高AD,
AB=AC ( 已知 ),
AD=AD (公共边) ,
∴ Rt△BAD ≌ Rt△CAD
∴ ∠B=∠C
已知: △ ABC中,AB=AC.
A
B
C
证明:等腰三角形的两个底角相等
D
求证: ∠B=∠C.
∴ ∠ADB =∠ADC=90°.
在Rt△BAD和Rt△CAD中,
(HL).
(全等三角形的对应角相等).
证法二
证明:
作顶角∠BAC的平分线AD,
AB=AC ( 已知 ),
∠1=∠2
AD=AD (公共边) ,
∴ △BAD≌△CAD
∴ ∠B=∠C
已知: △ ABC中,AB=AC.
A
B
C
1
2
证明:等腰三角形的两个底角相等
D
求证: ∠B=∠C.
∴ ∠1 = ∠2.
在△BAD和△CAD中,
(SAS).
(全等三角形的对应角相等).
证法三
等腰三角形的性质
A
B
C
应用格式:
在△ABC中
∵ AB=AC
∴ ∠B=∠C
的两个底角相等.
等腰三角形
(可以简称:等边对等角)
(等边对等角)
证明:
过点A作BC的垂直平分线AD.
已知: △ ABC中,AB=AC.
A
B
C
1
2
D
求证: ∠B= ∠C.
×
过点A作BC的垂线AD.
过点A作∠BAC的平分线AD.
过点A作BC的中线AD.
√
√
√
注意作图语言的规范表述
证明:
作顶角∠BAC的平分线AD,
AB=AC ( 已知 ),
∠ 1= ∠ 2
AD=AD (公共边) ,
∴ △BAD ≌ △CAD
∴ BD=CD,
A
B
C
1
2
D
∴ ∠1 = ∠2.
在△BAD和△CAD中,
(SAS).
∠ADB=∠ADC.
∵∠ADB +∠ADC=180°,
∴∠ADB=90°.
∴AD垂直平分BC.
∴ ∠B=∠C
还可推出什么结论?
等腰三角形顶角平分线垂直平分底边.
等腰三角形的性质2
等腰三角形顶角平分线垂直平分底边.
等腰三角形的顶角平分线、底边上的中线、 底边上的高互相重合.
A
B
C
1
2
D
(简写成三线合一)
学习新知
等腰三角形的性质
性质 1 等腰三角形的两个底角相等.
(简写成等边对等角)
性质 2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合.
(简写成三线合一)
A
B
C
1
2
D
“三线合一”
A
B
C
D
(1) 在△ABC中, AB=AC,
AD⊥BC,
∴____⊥____ ,∠_____ =∠_____.
∴____ ⊥____ ,_____ =_____.
∴∠_____ = ∠_____,____= ____.
(2) 在△ABC中, AB=AC,
(3) 在△ABC中, AB=AC,
∠BAD =∠CAD ,
BD=DC,
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
练习巩固
例1 已知:如图,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.
A
B
C
D
E
要求:
AB=AC
∠B=∠C
∠DAB=∠B
∠EAC=∠C
∠DAE
∠DAB =? ∠EAC=?
例题解析
例1 已知:如图,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.
A
B
C
D
E
解:
∵AB=AC,
∴∠B=∠C.
∵∠BAC=120°,
∴∠B=∠C
∵BD=AD,
CE=AE,
∴∠DAB=∠B=30°,
∠EAC=∠C=30°.
∴∠DAE
=∠BAC-∠DAB-∠EAC
=120°-30°-30°
=60°
=30°
= ×(180°-120°)
1
2
1.如图,△ABC中, AB=AC,AD=BD, DE⊥AB
于点E,若BC=10 ,且△BDC的周长为24,求AE
的长.
巩固提高
解:
∵BC=10,
∴BD+CD=14.
B
A
D
E
C
△BDC的周长为24,
∵AD=BD,
∴AD+CD=AC=14.
∵AB=AC,
∴AB=14.
∵AD=BD,DE⊥AB,
∴AE= AB=7.
1
2
2.如图,△ABC中, AB=AC,点D在且△ABC外,
CD⊥AD于D,CD= BC,求证: ∠ACD=∠B.
1
2
B
A
D
C
证明:
E
过点A作AE⊥BC于E,
AB=AC
BE=CD
∴ Rt△ABE ≌ Rt△ACD
∴ ∠ACD=∠B.
∴ ∠AEB =90°.
在Rt△ABE和Rt△ACD中,
(HL).
∴ ∠AEB =∠ADC=90°.
∴ ∠ADC=90°.
∵CD⊥AD,
∵AB=AC,
∴BE= BC.
1
2
∵CD= BC,
∴BE=CD
1
2
课堂小结
1.我们学习了等腰三角形哪些性质?
2.运用等腰三角形的性质解题时要注意什么?
1.如图,在△ABC中,AB=AC,BD平分∠ABC,
BD=BE,∠A=84°,则∠DEC= .
B
A
D
E
C
巩固提高
114°
2.如图,CE平分∠ACB,且CE⊥BD,DA=DB,
AC=18,△CDB的周长为28,则BE的长为 .
B
C
D
E
A
5
3.如图,在等腰△ABC中,∠ABC=90°,D为
AC边上中点,过D点作DE⊥DF,交AB于E,
交BC于F,若AE=4,FC=3,则△ABC的面积
为 .
B
A
D
E
C
F
49
2
△ADE ≌△BDF
△BDE ≌△CDF
提示:连接BD
今天作业
课本P139页第1、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
