15.3 等腰三角形 (3) 课件(共25张PPT)
文档属性
| 名称 | 15.3 等腰三角形 (3) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
沪科版 八年级上册
15. 3 等腰三角形(3)
1.掌握等腰三角形两底角相等的性质;
2.掌握等腰三角形顶角平分线与底边上的高,底边上的中线三线合一的性质.
教学重点:
运用等腰三角形性质解题.
教学难点:
等腰三角形性质的证明.
教学目标:
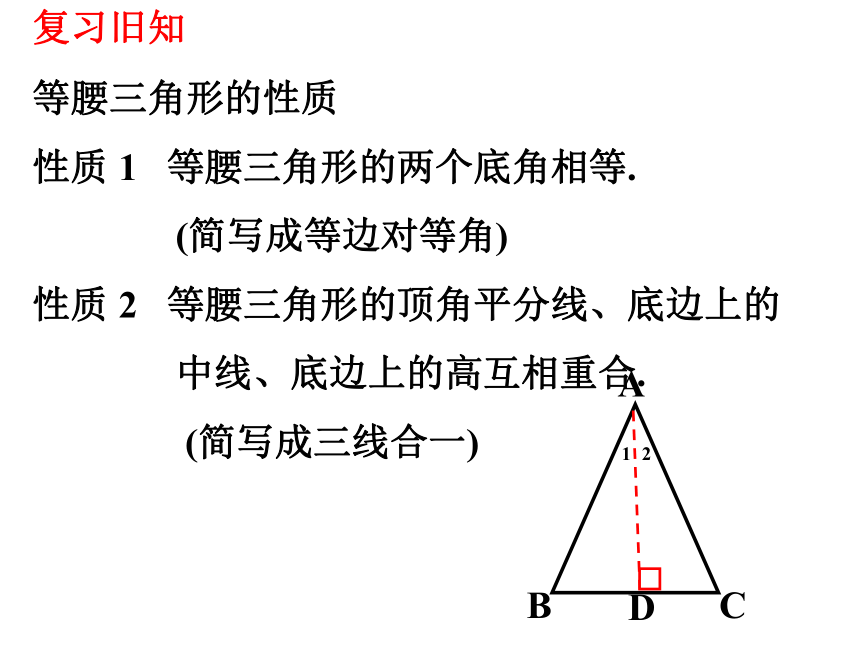
等腰三角形的性质
性质 1 等腰三角形的两个底角相等.
(简写成等边对等角)
性质 2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合.
(简写成三线合一)
A
B
C
1
2
D
复习旧知
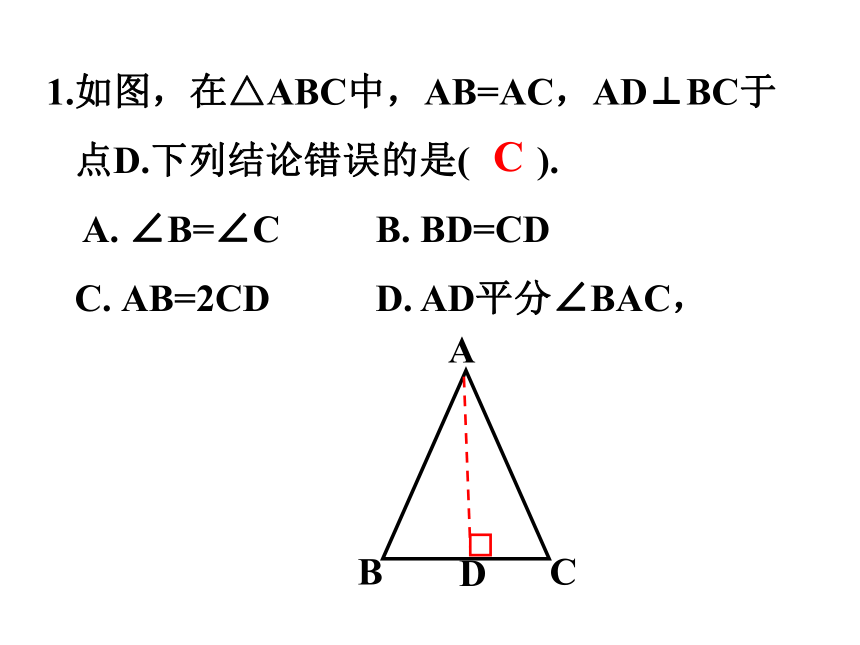
1.如图,在△ABC中,AB=AC,AD⊥BC于
点D.下列结论错误的是( ).
A. ∠B=∠C B. BD=CD
C. AB=2CD D. AD平分∠BAC,
A
B
C
D
C
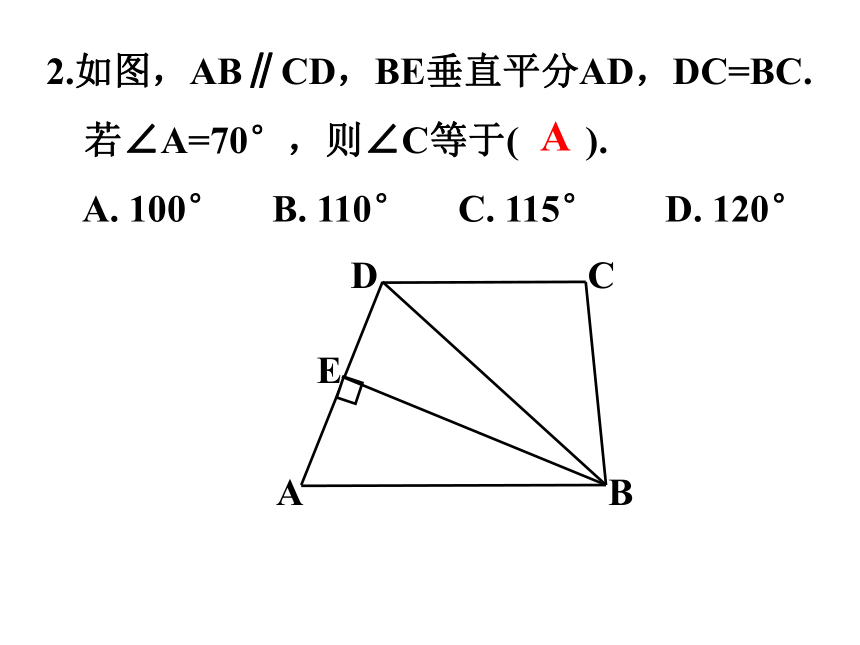
2.如图,AB∥CD,BE垂直平分AD,DC=BC.
若∠A=70°,则∠C等于( ).
A. 100° B. 110° C. 115° D. 120°
A
A
B
C
D
E
等腰三角形的两个底角相等.
这个定理的逆命题是什么?
如果一个三角形有两个角相等,
3.猜想这个命题正确吗?
那么这个三角形是等腰三角形。
题设:
如果一个三角形是等腰三角形
结论:
那么它的两个底角相等
题设:
结论:
探究新知
A
B
C
题设:
结论:
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
已知:△ABC中,∠B=∠C.
求证:AB=AC
探究新知
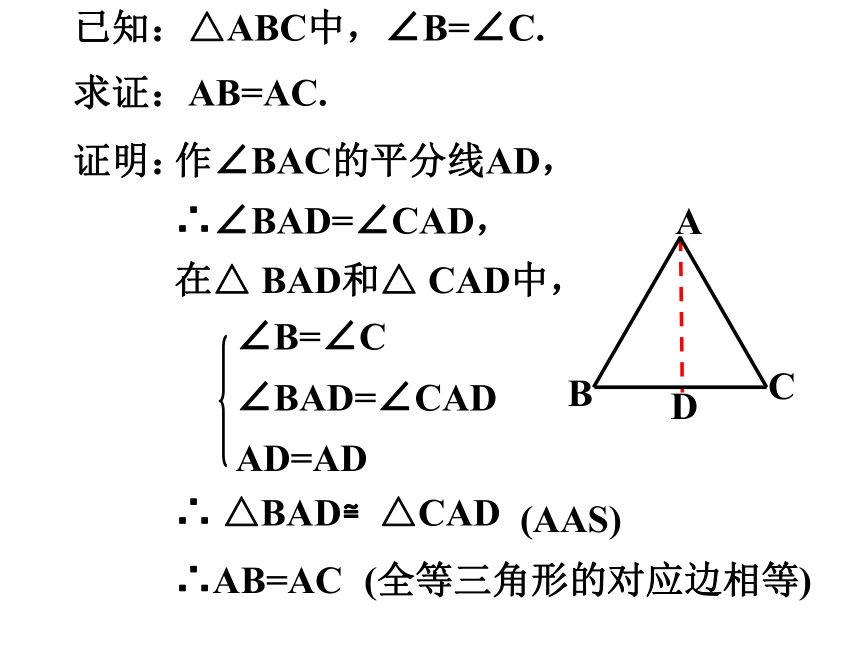
已知:△ABC中,∠B=∠C.
求证:AB=AC.
证明:
作∠BAC的平分线AD,
在△ BAD和△ CAD中,
∠B=∠C
∴ △BAD≌△CAD
∴AB=AC
A
B
C
D
AD=AD
∠BAD=∠CAD
∴∠BAD=∠CAD,
(AAS)
(全等三角形的对应边相等)
已知:△ABC中,∠B=∠C.
求证:AB=AC
证明:
作∠BAC的平分线AD
在△ BAD和△ CAD中,
∠B=∠C
∴ △BAD≌△CAD
∴AB=AC
A
B
C
D
思考:作底边上的高可以吗
AD=AD
∠BAD=∠CAD
∴∠BAD=∠CAD,
作底边中线呢
(AAS)
(全等三角形的对应边相等)
已知:△ABC中,∠B=∠C.
求证:AB=AC.
证明:
作BC边上的高AD
在△BAD和△CAD中,
∠B=∠C,
∴ △BAD≌△CAD
∴AB=AC
A
B
C
D
AD=AD
∠BAD=∠CAD,
∴∠BAD=∠CAD=90°,
(AAS)
(全等三角形的对应边相等)
已知:△ABC中,∠B=∠C.
求证:AB=AC.
证明:
作BC边的中线AD,
在△BAD和△CAD中,
∠B=∠C,
A
B
C
D
AD=AD
BD=CD,
∴ BD=CD,
不可证
△BAD与△CAD
全等
(SSA)
×
等腰三角形的判定方法
A
B
C
应用格式:
在△ABC中
∵ ∠B=∠C
∴ AB=AC
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
(可以简称:等角对等边)
(等角对等边)
B
A
D
C
例1 已知:如图,AD ∥BC,BD平分∠ABC.
求证:AB=AD.
要证:
例题解析
AB=AD
∠ABD=∠ADB
∠ADB=∠DBC
AD ∥BC
B
A
D
C
例1 已知:如图,AD ∥BC,BD平分∠ABC.
求证:AB=AD.
∵ AD ∥BC ,
∴∠ADB=∠DBC.
∵BD 平分∠ ABC,
∴∠ABD=∠DBC.
∴∠ABD=∠ADB,
∴AB=AD
证明:
(等角对等边).
例题解析
例2 如图,AC和BD相交于点O,AB∥DC,
OA=OB. 求证:OC=OD.
B
A
D
C
O
要证:
OC = OD
∠C=∠D
AB∥DC
∠A=∠C
∠B =∠D
OA=OB
∠A=∠B
例2 如图,AC和BD相交于点O,AB∥DC,OA=OB. 求证:OC=OD.
B
A
D
C
O
证明:
∵AB∥DC,
∴∠A=∠C,
∠B =∠D.
∵OA = OB,
∴∠A=∠B
∴OC = OD
∴∠C=∠D,
(等角对等边).
(等边对角等).
1.已知:如图, AB与CD交于点P,CP=PD,
∠A=42°, ∠CPB=138°,∠B=69°,
求证:AC=PB.
B
A
D
C
P
练习巩固
AC=PB
CP=PD
AC=CP
PB=PD
要证:
∠A=∠APC
∠D=∠B
∠APC=42°
∠D=69°
1.已知:如图, AB与CD交于点P,CP=PD,∠A=42°, ∠CPB=138°,∠B=69°,求证:AC=PB.
∵ ∠CPB+∠APC =180°,
∴∠APC =180°-∠CPB
=180°-138°
=42°.
∵ ∠A =42°,
∴∠A=∠APC,
∴CP=AC,
∵ ∠CPB=∠B+∠D ,
∴∠ D=∠CPB-∠B
=138°-69°
=69°.
∴∠ D=∠B,
∴PD=PB.
∵ CP=PD,
∴AC=PB.
解:
B
A
D
C
P
∠B =69°,
2.已知:△ABC中,AB=AC,AD平分∠BAC交
BC于点D,若∠B=45°,BC=10cm. 求AD的长度.
解:
∵AB=AC,
AD平分∠BAC,
∴AD也是BC边上的高和中线.
∴BD= BC=5cm,
∠ADB=90°.
∵ ∠B=45°,
∴∠BAD =∠B.
∴AD=BD
=5cm.
∴∠BAD =45°.
1
2
B
A
D
C
课堂小结
1.如何判定一个三角形是等腰三角形?
2.运用等角对等边判定等腰三角形时要注意什么?
1.在△ABC中, ∠A=70° , ∠B=40°,
∠C=70°.则( ).
A. AB=AC B. AC=BC
C. AB=BC D. AB=AC=BC,
C
巩固新知
2.在△ABC中, ∠A=100° , 当∠B= 时,
△ABC是等腰三角形.
40°
3.如图,AD平分∠BAC, AD⊥BD于点D,
DE∥AC. 求证: △BDE是等腰三角形.
证明:
∵AD平分∠BAC,
∴∠EDA +∠EDB=∠ADB=90°.
∵ AD⊥BD于点D,
∴∠BAD =∠CAD.
∴∠BDA =90°.
B
A
D
C
E
∵DE∥AC,
∴∠EDA =∠CAD.
∴∠BAD =∠EDA.
∠BAD+∠B=90°.
∴∠EDB =∠B.
∴△BDE是等腰三角形.
今天作业
课本P139页第5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
15. 3 等腰三角形(3)
1.掌握等腰三角形两底角相等的性质;
2.掌握等腰三角形顶角平分线与底边上的高,底边上的中线三线合一的性质.
教学重点:
运用等腰三角形性质解题.
教学难点:
等腰三角形性质的证明.
教学目标:
等腰三角形的性质
性质 1 等腰三角形的两个底角相等.
(简写成等边对等角)
性质 2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合.
(简写成三线合一)
A
B
C
1
2
D
复习旧知
1.如图,在△ABC中,AB=AC,AD⊥BC于
点D.下列结论错误的是( ).
A. ∠B=∠C B. BD=CD
C. AB=2CD D. AD平分∠BAC,
A
B
C
D
C
2.如图,AB∥CD,BE垂直平分AD,DC=BC.
若∠A=70°,则∠C等于( ).
A. 100° B. 110° C. 115° D. 120°
A
A
B
C
D
E
等腰三角形的两个底角相等.
这个定理的逆命题是什么?
如果一个三角形有两个角相等,
3.猜想这个命题正确吗?
那么这个三角形是等腰三角形。
题设:
如果一个三角形是等腰三角形
结论:
那么它的两个底角相等
题设:
结论:
探究新知
A
B
C
题设:
结论:
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
已知:△ABC中,∠B=∠C.
求证:AB=AC
探究新知
已知:△ABC中,∠B=∠C.
求证:AB=AC.
证明:
作∠BAC的平分线AD,
在△ BAD和△ CAD中,
∠B=∠C
∴ △BAD≌△CAD
∴AB=AC
A
B
C
D
AD=AD
∠BAD=∠CAD
∴∠BAD=∠CAD,
(AAS)
(全等三角形的对应边相等)
已知:△ABC中,∠B=∠C.
求证:AB=AC
证明:
作∠BAC的平分线AD
在△ BAD和△ CAD中,
∠B=∠C
∴ △BAD≌△CAD
∴AB=AC
A
B
C
D
思考:作底边上的高可以吗
AD=AD
∠BAD=∠CAD
∴∠BAD=∠CAD,
作底边中线呢
(AAS)
(全等三角形的对应边相等)
已知:△ABC中,∠B=∠C.
求证:AB=AC.
证明:
作BC边上的高AD
在△BAD和△CAD中,
∠B=∠C,
∴ △BAD≌△CAD
∴AB=AC
A
B
C
D
AD=AD
∠BAD=∠CAD,
∴∠BAD=∠CAD=90°,
(AAS)
(全等三角形的对应边相等)
已知:△ABC中,∠B=∠C.
求证:AB=AC.
证明:
作BC边的中线AD,
在△BAD和△CAD中,
∠B=∠C,
A
B
C
D
AD=AD
BD=CD,
∴ BD=CD,
不可证
△BAD与△CAD
全等
(SSA)
×
等腰三角形的判定方法
A
B
C
应用格式:
在△ABC中
∵ ∠B=∠C
∴ AB=AC
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
(可以简称:等角对等边)
(等角对等边)
B
A
D
C
例1 已知:如图,AD ∥BC,BD平分∠ABC.
求证:AB=AD.
要证:
例题解析
AB=AD
∠ABD=∠ADB
∠ADB=∠DBC
AD ∥BC
B
A
D
C
例1 已知:如图,AD ∥BC,BD平分∠ABC.
求证:AB=AD.
∵ AD ∥BC ,
∴∠ADB=∠DBC.
∵BD 平分∠ ABC,
∴∠ABD=∠DBC.
∴∠ABD=∠ADB,
∴AB=AD
证明:
(等角对等边).
例题解析
例2 如图,AC和BD相交于点O,AB∥DC,
OA=OB. 求证:OC=OD.
B
A
D
C
O
要证:
OC = OD
∠C=∠D
AB∥DC
∠A=∠C
∠B =∠D
OA=OB
∠A=∠B
例2 如图,AC和BD相交于点O,AB∥DC,OA=OB. 求证:OC=OD.
B
A
D
C
O
证明:
∵AB∥DC,
∴∠A=∠C,
∠B =∠D.
∵OA = OB,
∴∠A=∠B
∴OC = OD
∴∠C=∠D,
(等角对等边).
(等边对角等).
1.已知:如图, AB与CD交于点P,CP=PD,
∠A=42°, ∠CPB=138°,∠B=69°,
求证:AC=PB.
B
A
D
C
P
练习巩固
AC=PB
CP=PD
AC=CP
PB=PD
要证:
∠A=∠APC
∠D=∠B
∠APC=42°
∠D=69°
1.已知:如图, AB与CD交于点P,CP=PD,∠A=42°, ∠CPB=138°,∠B=69°,求证:AC=PB.
∵ ∠CPB+∠APC =180°,
∴∠APC =180°-∠CPB
=180°-138°
=42°.
∵ ∠A =42°,
∴∠A=∠APC,
∴CP=AC,
∵ ∠CPB=∠B+∠D ,
∴∠ D=∠CPB-∠B
=138°-69°
=69°.
∴∠ D=∠B,
∴PD=PB.
∵ CP=PD,
∴AC=PB.
解:
B
A
D
C
P
∠B =69°,
2.已知:△ABC中,AB=AC,AD平分∠BAC交
BC于点D,若∠B=45°,BC=10cm. 求AD的长度.
解:
∵AB=AC,
AD平分∠BAC,
∴AD也是BC边上的高和中线.
∴BD= BC=5cm,
∠ADB=90°.
∵ ∠B=45°,
∴∠BAD =∠B.
∴AD=BD
=5cm.
∴∠BAD =45°.
1
2
B
A
D
C
课堂小结
1.如何判定一个三角形是等腰三角形?
2.运用等角对等边判定等腰三角形时要注意什么?
1.在△ABC中, ∠A=70° , ∠B=40°,
∠C=70°.则( ).
A. AB=AC B. AC=BC
C. AB=BC D. AB=AC=BC,
C
巩固新知
2.在△ABC中, ∠A=100° , 当∠B= 时,
△ABC是等腰三角形.
40°
3.如图,AD平分∠BAC, AD⊥BD于点D,
DE∥AC. 求证: △BDE是等腰三角形.
证明:
∵AD平分∠BAC,
∴∠EDA +∠EDB=∠ADB=90°.
∵ AD⊥BD于点D,
∴∠BAD =∠CAD.
∴∠BDA =90°.
B
A
D
C
E
∵DE∥AC,
∴∠EDA =∠CAD.
∴∠BAD =∠EDA.
∠BAD+∠B=90°.
∴∠EDB =∠B.
∴△BDE是等腰三角形.
今天作业
课本P139页第5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
