人教版必修2《6.3 向心加速度》2022年同步练习卷(含答案)
文档属性
| 名称 | 人教版必修2《6.3 向心加速度》2022年同步练习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 723.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-14 14:30:28 | ||
图片预览



文档简介
人教版必修2《5.5 向心加速度》2022年同步练习卷
一 、单选题(本大题共14小题,共84分)
1.(6分)[人大附中高一月考]某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为、、,若甲轮的角速度大小为,则丙轮的角速度大小为( )
A. B. C. D.
2.(6分)下列关于向心加速度和向心力的说法中正确的是
A. 向心加速度的方向始终沿半径指向圆心
B. 在匀速圆周运动中,向心加速度是恒定的
C. 向心力既可以改变线速度的方向,又可以改变线速度的大小
D. 物体受到向心力的作用才能做圆周运动
3.(6分)计算机中的硬磁盘磁道如图所示,硬磁盘绕磁道的圆心转动,、两点位于不同的磁道上,线速度分别为和,向心加速度分别为和,则它们大小关系正确的是( )
A. B.
C. D.
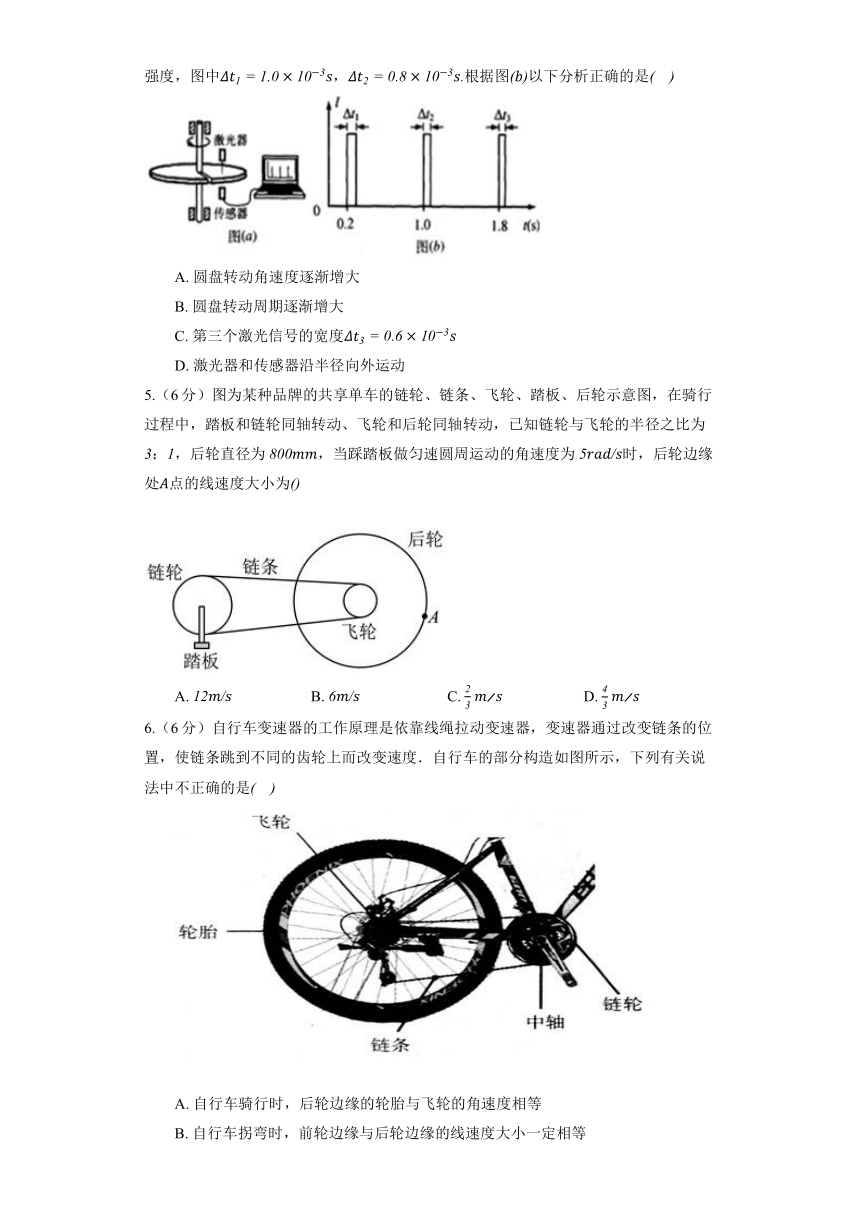
4.(6分)一水平放置的圆盘绕竖直固定轴转动,在圆盘上沿半径方向开有一条宽度为的均匀狭缝,将激光器与传感器上下对准,使二者间连线与转轴平行,分别置于圆盘的上下两侧,且可以同步地沿圆盘半径方向匀速移动,激光器连续向下发射激光束。在圆盘转动过程中,当狭缝经过激光器与传感器之间时,传感器接收到一个激光信号,并将其输入计算机,经处理后画出相应图线。图为该装置示意图,图为所接收的光信号随时间变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,图中,根据图以下分析正确的是
A. 圆盘转动角速度逐渐增大
B. 圆盘转动周期逐渐增大
C. 第三个激光信号的宽度
D. 激光器和传感器沿半径向外运动
5.(6分)图为某种品牌的共享单车的链轮、链条、飞轮、踏板、后轮示意图,在骑行过程中,踏板和链轮同轴转动、飞轮和后轮同轴转动,已知链轮与飞轮的半径之比为:,后轮直径为,当踩踏板做匀速圆周运动的角速度为时,后轮边缘处点的线速度大小为
A. B. C. D.
6.(6分)自行车变速器的工作原理是依靠线绳拉动变速器,变速器通过改变链条的位置,使链条跳到不同的齿轮上而改变速度.自行车的部分构造如图所示,下列有关说法中不正确的是
A. 自行车骑行时,后轮边缘的轮胎与飞轮的角速度相等
B. 自行车拐弯时,前轮边缘与后轮边缘的线速度大小一定相等
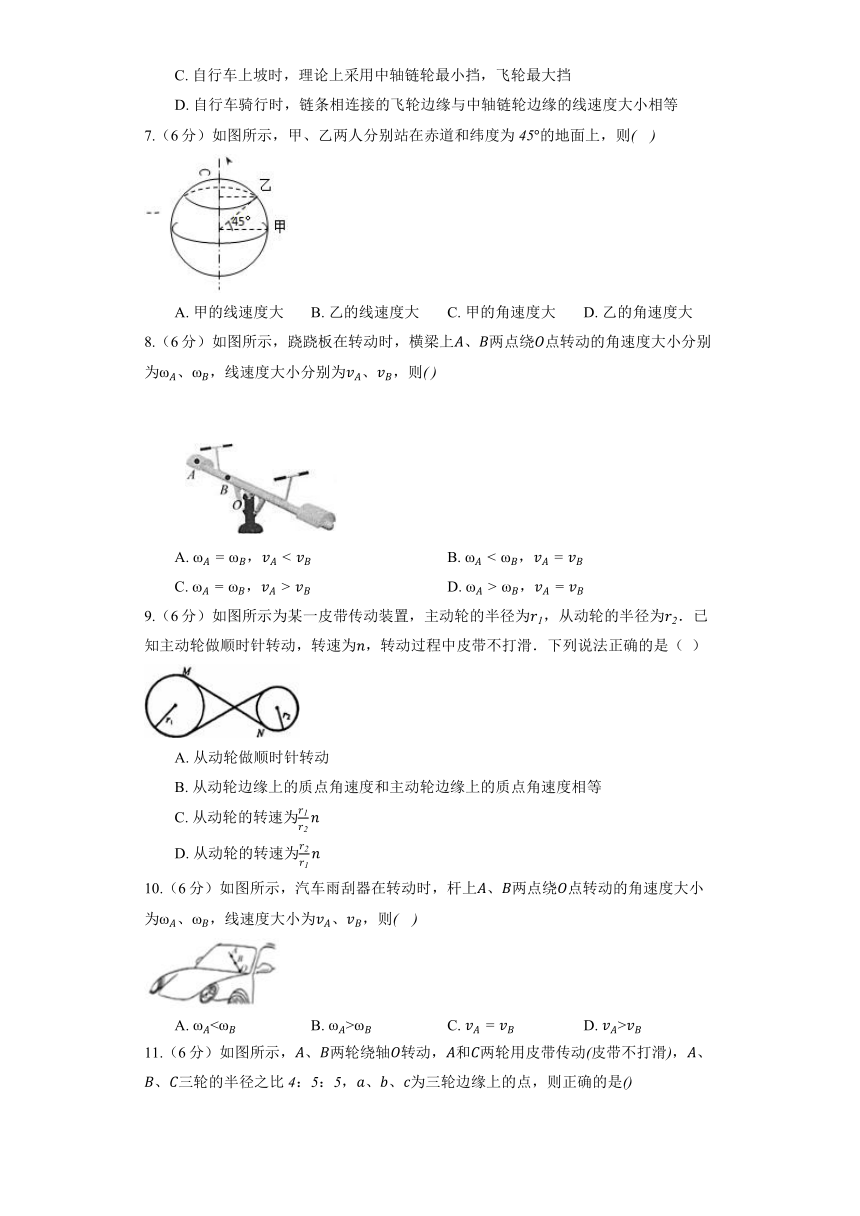
C. 自行车上坡时,理论上采用中轴链轮最小挡,飞轮最大挡
D. 自行车骑行时,链条相连接的飞轮边缘与中轴链轮边缘的线速度大小相等
7.(6分)如图所示,甲、乙两人分别站在赤道和纬度为的地面上,则
A. 甲的线速度大 B. 乙的线速度大 C. 甲的角速度大 D. 乙的角速度大
8.(6分)如图所示,跷跷板在转动时,横梁上、两点绕点转动的角速度大小分别为、,线速度大小分别为、,则
A. , B. ,
C. , D. ,
9.(6分)如图所示为某一皮带传动装置,主动轮的半径为,从动轮的半径为.已知主动轮做顺时针转动,转速为,转动过程中皮带不打滑.下列说法正确的是( )
A. 从动轮做顺时针转动
B. 从动轮边缘上的质点角速度和主动轮边缘上的质点角速度相等
C. 从动轮的转速为
D. 从动轮的转速为
10.(6分)如图所示,汽车雨刮器在转动时,杆上、两点绕点转动的角速度大小为、,线速度大小为、,则
A. B. C. D.
11.(6分)如图所示,、两轮绕轴转动,和两轮用皮带传动皮带不打滑,、、三轮的半径之比::,、、为三轮边缘上的点,则正确的是
A. 线速度
B. 角速度
C. 角速度
D. 向心加速度
12.(6分)学校门口的车牌自动识别系统如图所示,闸杆距地面高为,可绕转轴在竖直面内匀速转动;自动识别区到的距离为。汽车以速度匀速驶入自动识别区,识别的反应时间为;若汽车可看成高的长方体,闸杆转轴与车左侧面水平距离为。要使汽车匀速顺利通过,闸杆转动的角速度至少为
A. B. C. D.
13.(6分)一物体做匀速圆周运动的半径为,线速度大小为,角速度为,周期为下列关于这些物理量的关系式中,正确的是
A. B. C. D.
14.(6分)年北京冬奥会短道速滑比赛决出首枚金牌,男女米混合接力决赛,由范可新、曲春雨、任子威和武大靖出战的中国队,滑出分秒的成绩,获得中国代表团本届冬奥会的首枚金牌,也是短道速滑项目的首枚金牌。如图所示为我国选手武大靖在比赛中的精彩瞬间,假定他正沿圆弧形弯道做匀速圆周运动,则他运动过程中
A. 线速度恒定 B. 加速度恒定
C. 相等时间内经过的位移相同 D. 相等时间内转过的角度相同
二 、多选题(本大题共7小题,共42分)
15.(6分)两颗人造卫星绕地球做匀速圆周运动,它们的质量之比为,轨道半径之比,则下列说法正确的是
A. 它们的线速度之比为
B. 它们的向心加速度之比为
C. 它们的向心力之比为
D. 它们的周期之比为
16.(6分)小球做匀速圆周运动半径为,向心加速度为,则下列正确的是( )
A. 小球的角速度 B. 小球运动的周期
C. 时间内小球通过的路程 D. 时间内小球转过的角度
17.(6分)机器由电动机带动,机器皮带轮的半径是电动机皮带轮半径的倍,、为两轮边缘上的点,为机器皮带轮半径的中点,皮带与两轮之间不发生相对滑动,则下列说法正确的是
A. ,线速度大小之比
B. ,角速度大小之比
C. ,周期之比
D. ,向心加速度大小之比
18.(6分)一质点做匀速圆周运动,下列说法中正确的是
A. 任意相等时间内,通过的弧长相等
B. 任意相等时间内,转过的角度相等
C. 任意相等时间内,通过的位移相同
D. 任意相等时间内,速度的变化相同
19.(6分)如图所示是两个做圆锥摆运动的小球、小球,摆线跟竖直方向的夹角分别为和,两球做匀速圆周运动所在的水平面到各自悬点的距离之比为,下列有关判断正确的是( )
A. 两球运动周期之比为 B. 两球运动线速度之比为
C. 两球运动角速度之比为 D. 两球运动向心加速度之比为
20.(6分)甲、乙两个物体分别放在惠州和哈尔滨,将它们随地球一起转动的运动当作匀速圆周运动,下列说法正确的是
A. 甲的角速度一定较大
B. 甲的线速度一定较大
C. 甲的向心加速度一定较大
D. 甲所需的向心力一定较大
21.(6分)一半径为的球形行星绕其自转轴匀速转动,若质量为的物体在该星球两极时的重力为,在赤道上的重力为,则
A. 该星球自转的角速度大小为
B. 环绕该星球表面做匀速圆周运动的卫星的速率为
C. 环绕该星球表面做匀速圆周运动的卫星的速率为
D. 放置于此星球表面纬度为处的物体,向心加速度大小为
三 、简答题(本大题共3小题,共5分)
22.(5分)如图所示,轮、固定在一转轴上,轮、用皮带连接且不打滑。在、、三个轮的边缘各取一点、、,已知三个轮的半径比=,求:
22-1.、、三点的线速度大小之比。
22-2.、、三点的角速度之比。
22-3.、、三点的向心加速度大小之比。
答案和解析
1.【答案】A;
【解析】齿轮啮合,两齿轮边缘上各点的线速度大小相等,由题图可知甲、丙两轮边缘上各点的线速度大小相等。根据公式,得, 则丙轮的角速度大小,故选项A正确。
2.【答案】A;
【解析】解:、向心力的方向始终指向圆心,所以,向心加速度的方向也始终沿半径指向圆心,故A正确;
B、向心加速度的方向时刻指向圆心,方向改变,是变量,故B错误;
C、向心力总是垂直于速度,故只能改变物体的运动方向,不能改变物体运动速度的大小,故C错误;
D、物体做匀速圆周运动时,合力总是指向圆心,故又称向心力,是按照力的作用效果命名的,故D错误;
故选:.
做匀速圆周运动的物体要受到指向圆心的向心力的作用,从而产生指向圆心的向心加速度,向心加速度只改变物体的速度的方向不改变速度的大小.而非匀速圆周运动,合外力指向圆心的分量提供向心力.
匀速圆周运动要注意,其中的匀速只是指速度的大小不变,合力作为向心力始终指向圆心,合力的方向也是时刻在变化的.
3.【答案】A;
【解析】解:、是同轴转动角速度相同,根据,由图可知,可得,根据向心加速度公式,由图可知,可得,故正确,错误.
故选:.
4.【答案】D;
【解析】解:、由图线读得,转盘的转动周期,不变,故角速度,不变,故AB错误;
C、时刻的线速度:,时刻的线速度:,时刻的线速度:,
,解得,故C错误;
D、由于电脉冲信号宽度在逐渐变窄,表明光能通过狭缝的时间逐渐减少,即圆盘上对应探测器所在位置的线速度逐渐增加,因此激光器和探测器沿半径由中心向边缘移动,故D正确;
故选:。
由图得到圆盘的转动周期两次电脉冲信号的时间差,然后根据角速度定义公式求解圆盘转动的角速度;由图得到电脉冲信号宽度在逐渐变窄,说明线速度变大,结合公式进行判断即可。
考查圆周运动的角速度与周期的关系、角速度与线速度和半径关系,以及运用数学知识分析问题的能力,较难。
5.【答案】B;
【解析】
同轴传动角速度相等,同缘传动线速度相等,先结合判断后轮的角速度,然后再求解后轮边缘处点的线速度大小。
本题以某种品牌的共享单车为背景,考查链条传动问题,解决此题的关键是要明确同轴传动角速度相等,同缘传动线速度相等。
当踩踏板做匀速圆周运动的角速度为时,由于链轮与飞轮通过链条传动,边缘线速度大小相等,由公式可知,角速度与半径成反比,故飞轮的角速度为:,后轮的角速度与飞轮相等,可知后轮边缘处点的线速度大小为:,故正确,错误。
故选。
6.【答案】B;
【解析】
根据传动结构特点分析。
解答该题的关键是分析是哪一种转动,根据圆周运动解题。
A.自行车骑行时,后轮边缘的轮胎与飞轮的角速度相等,故A正确;
B.自行车拐弯时,由于前后轮的转弯半径不同,故前轮边缘与后轮边缘的线速度大小不相等,故B错误;
C.自行车上坡时,理论上采用中轴链轮最小挡,飞轮最大挡 ,线速度最小,最省力,故C正确;
D.自行车骑行时,链条相连接的飞轮边缘与中轴链轮边缘属于链条传动,故线速度大小相等,故D正确。
本题选不正确的,故选B。
7.【答案】A;
【解析】解:甲乙两物体角速度一样,同时由图可知:乙随地球转动的半径比甲小,根据:,可知甲的线速度大,故选项BCD错误,A正确。
故选:。
随地球自转的物体有两个共同点:一是角速度一样,二是圆心都在转轴上,根据这两点利用角速度和线速度关系即可求解。
该题考查了圆周运动中基本物理量角速度、线速度、半径之间关系,是一道基础性题目。
8.【答案】C;
【解析】分析:本题关键是明确同轴转动角速度相等,然后根据线速度与角速度关系公式比较线速度大小;也可以直接根据线速度和角速度的定义公式判断,基础题。
解答:跷跷板在转动时,横梁上、两点绕点转动属同轴转动,角速度相等,故有:
由于,根据,;
故正确,错误。
故选:。
同轴转动,角速度相等;根据判断线速度大小。
9.【答案】C;
【解析】解:.因为主动轮做顺时针转动,从动轮通过皮带的摩擦力带动转动,所以从动轮逆时针转动,故错误;
.由于通过皮带传动,皮带与轮边缘接触处质点的线速度相等,角速度不相等,故错误;
.根据得:
所以,故正确,错误.
故选:.
10.【答案】D;
【解析】解:杆上、两点绕点的转动属于同轴转动,所以角速度相等,故;
由于,根据,;故ABC错误,D正确。
故选:。
同轴转动,角速度相等;根据判断线速度大小。
本题关键是明确同轴转动角速度相等,然后根据线速度与角速度关系公式比较线速度大小;也可以直接根据线速度和角速度的定义公式判断,基础题。
11.【答案】D;
【解析】已知、、三轮的半径之间的关系;
、两个轮子是同轴传动,角速度相等,故,根据公式,线速度之比为;
根据公式,向心加速度之比为;
、两个轮子靠传送带传动,轮子边缘上的点具有相同的线速度,故::,根据公式,角速度之比为;
根据公式,可得。
A.结合以上分析结果可知,故错误;
角速度之比为,故、均错误;
D.三点的加速度之比为,故正确.
故选
12.【答案】A;
【解析】解:闸杆转动时间为
汽车匀速顺利通过,闸杆转动的角度至少为
解得
闸杆转动的角速度至少为,故正确,错误。
故选:。
求出汽车安全通过道闸时直杆转过的角度,然后求出直杆转动的角速度大小。
认真审题理解题意求出直杆转过的角度是解题的前提与关键,应用角速度的定义式即可解题。
13.【答案】D;
【解析】解:
、,故A错误,D正确;
、;故BC错误。
故选:。
直接根据线速度、角速度、周期的定义以及角度的定义出发展开讨论即可.
正确理解线速度的定义,角速度,弧长,能正确推导各量之间的关系是解决本题的关键.
14.【答案】D;
【解析】
、匀速圆周运动的线速度大小不变,方向在时刻发生变化,故错误;
、匀速圆周运动的加速度为向心加速度,大小保持不变,方向总是指向圆心,即加速度方向在时刻发生变化,故错误;
、匀速圆周运动的角速度保持不变,可知相等时间内转过的角度相同,对应的弦长相等,即经过的位移大小相等,但位移的方向不同,故错误,正确。
故选。
15.【答案】ABC;
【解析】
根据万有引力提供向心力,解出线速度、周期、角速度、加速度与轨道半径的关系,根据已知的半径求它们的比值。
此题主要考查了人造卫星的加速度、周期和轨道的关系。本题的关键是要掌握万有引力提供向心力,解出线速度、周期、加速度与轨道半径的关系。
根据万有引力提供向心力,解得:,,;所以:
A.根据,得,故正确;
B.根据,得,故正确;
C.根据,得,故正确;
D.根据,得,故错误。
故选。
16.【答案】BC;
【解析】.根据
可得,小球的角速度
A不符合题意;
B.根据
可得,小球运动的周期,符合题意;
C.根据,可得小球运动的速度
因此,时间内小球通过的路程,符合题意;
D.时间内小球转过的角度,不符合题意.
故答案为:.
17.【答案】BC;
【解析】
传动装置,在传动过程中不打滑,则有:共轴的角速度是相同的同一传动装置接触边缘的线速度大小是相等的所以当角速度一定时,线速度与半径成正比当线速度大小一定时,角速度与半径成反比因此根据题目条件可以知道加速度及角速度关系.
B.因与机器皮带边缘同轴转动,所以角速度相等,正确;
A.由,、角速度相同,所以,因电动机和机器由同一皮带连接,所以它们边缘线速度相等,所以,所以,错误;
C.因电动机和机器由同一皮带连接,所以它们边缘线速度相等设电动机半径为,角速度,机器轮半径为角速度为
根据题意知:,由得:所以,,由得:,正确;
D.由,,得:,错误。
故选。
18.【答案】AB;
【解析】该题有一定的综合性,在圆周运动中考察标量和矢量这两种物理量的特点,同时考察了匀速圆周运动的特点,用描述圆周运动的物理量和特点分析即可。
物理知识的学习过程中要前后融会贯通,不能是孤立的,明确各物理量的特点.如本题中在圆周运动中矢量、标量问题。A.匀速圆周运动中速度的大小不变,只是速度方向改变,因此在任意相等时间内,通过的弧长是相等的,故正确;匀速圆周运动角速度不变,可知相等时间转过的角度相等,故正确;C.位移大小等于由初位置指向末位置有向线段长度,线段的方向即为位移方向,是矢量,因此在任意相等时间内,位移不一定相同,故错误;
速度是矢量,速度的变化量为,方向由指向即减数指向被减数,因此在任意相等时间内速度的变化不一定相同,故错误。故选。
19.【答案】ACD;
【解析】由题可知,可以设两个小球的质量都是;设球做匀速圆周运动所在的水平面到悬点的距离为,则球做匀速圆周运动所在的水平面到悬点的距离为,则球做圆周运动的半径:==,球做圆周运动的半径:=
以球为研究对象,根据重力与绳子的拉力的合力提供向心力,可得:=,解得:
同理,以球为研究对象,可得:
、两球运动的角速度之比:,根据,两球的周期之比:,故正确;
、两球的线速度之比:,故错误;
、根据公式:=.则:,故正确。
20.【答案】BC;
【解析】
地球上的任何的物体转动的角速度都和地球一样,但是在不同的地方,由于物体做圆周运动的半径不一样,线速度的大小不一样。随着地球一起绕地轴转动,说明它们的角速度是一样的,这是解本题的关键条件,再由线速度角速度的关系就可以做出判断了。
地球上的任何的物体转动的角速度都和地球一样,但是在不同的地方,由于物体做圆周运动的半径不一样,线速度的大小不一样,甲的半径大,线速度一定较大,故错误,正确;C.向心加速度,甲的向心加速度一定较大,故正确;
D.甲乙两个质量不知道大小,无法确定所需的向心力大小,故错误。
故选。
21.【答案】ACD;
【解析】
在两极,万有引力等于重力,在赤道,万有引力的一个分力等于重力,另一个分力提供向心力,结合牛顿第二定律求出星球自转的角速度.根据万有引力等于重力、万有引力提供向心力求出环绕星球表面做匀速圆周运动的卫星速率.根据几何关系求出在星球表面纬度为处物体转动的半径,结合向心加速度公式求出向心加速度的大小。
解决本题的关键知道在两极和赤道处万有引力和重力的关系,掌握万有引力定律的两个重要理论,并能灵活运用,难度中等。
A.在两极,万有引力等于重力,有:,在赤道,有:,联立两式解得,故正确;
根据得,,又,解得,故错误,正确;
D.处于星球表面纬度为处的物体,绕地轴转动的半径,则向心加速度,故正确。
故选。
22.【答案】、、三点的线速度大小之比=。;、、三点的角速度之比=。;、、三点的向心加速度大小之比=。;
【解析】、两点靠传送带传动,线速度大小相等,、共轴转动,角速度相等,根据=,则==。
所以、、三点的线速度大小之比=。
、共轴转动,角速度相等,、两点靠传送带传动,线速度大小相等,根据=,==.所以、、三点的角速度之比=。
、的线速度相等,根据,知==.、的角速度相等,根据=得,==.所以、、三点的向心加速度大小之比=。
一 、单选题(本大题共14小题,共84分)
1.(6分)[人大附中高一月考]某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为、、,若甲轮的角速度大小为,则丙轮的角速度大小为( )
A. B. C. D.
2.(6分)下列关于向心加速度和向心力的说法中正确的是
A. 向心加速度的方向始终沿半径指向圆心
B. 在匀速圆周运动中,向心加速度是恒定的
C. 向心力既可以改变线速度的方向,又可以改变线速度的大小
D. 物体受到向心力的作用才能做圆周运动
3.(6分)计算机中的硬磁盘磁道如图所示,硬磁盘绕磁道的圆心转动,、两点位于不同的磁道上,线速度分别为和,向心加速度分别为和,则它们大小关系正确的是( )
A. B.
C. D.
4.(6分)一水平放置的圆盘绕竖直固定轴转动,在圆盘上沿半径方向开有一条宽度为的均匀狭缝,将激光器与传感器上下对准,使二者间连线与转轴平行,分别置于圆盘的上下两侧,且可以同步地沿圆盘半径方向匀速移动,激光器连续向下发射激光束。在圆盘转动过程中,当狭缝经过激光器与传感器之间时,传感器接收到一个激光信号,并将其输入计算机,经处理后画出相应图线。图为该装置示意图,图为所接收的光信号随时间变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,图中,根据图以下分析正确的是
A. 圆盘转动角速度逐渐增大
B. 圆盘转动周期逐渐增大
C. 第三个激光信号的宽度
D. 激光器和传感器沿半径向外运动
5.(6分)图为某种品牌的共享单车的链轮、链条、飞轮、踏板、后轮示意图,在骑行过程中,踏板和链轮同轴转动、飞轮和后轮同轴转动,已知链轮与飞轮的半径之比为:,后轮直径为,当踩踏板做匀速圆周运动的角速度为时,后轮边缘处点的线速度大小为
A. B. C. D.
6.(6分)自行车变速器的工作原理是依靠线绳拉动变速器,变速器通过改变链条的位置,使链条跳到不同的齿轮上而改变速度.自行车的部分构造如图所示,下列有关说法中不正确的是
A. 自行车骑行时,后轮边缘的轮胎与飞轮的角速度相等
B. 自行车拐弯时,前轮边缘与后轮边缘的线速度大小一定相等
C. 自行车上坡时,理论上采用中轴链轮最小挡,飞轮最大挡
D. 自行车骑行时,链条相连接的飞轮边缘与中轴链轮边缘的线速度大小相等
7.(6分)如图所示,甲、乙两人分别站在赤道和纬度为的地面上,则
A. 甲的线速度大 B. 乙的线速度大 C. 甲的角速度大 D. 乙的角速度大
8.(6分)如图所示,跷跷板在转动时,横梁上、两点绕点转动的角速度大小分别为、,线速度大小分别为、,则
A. , B. ,
C. , D. ,
9.(6分)如图所示为某一皮带传动装置,主动轮的半径为,从动轮的半径为.已知主动轮做顺时针转动,转速为,转动过程中皮带不打滑.下列说法正确的是( )
A. 从动轮做顺时针转动
B. 从动轮边缘上的质点角速度和主动轮边缘上的质点角速度相等
C. 从动轮的转速为
D. 从动轮的转速为
10.(6分)如图所示,汽车雨刮器在转动时,杆上、两点绕点转动的角速度大小为、,线速度大小为、,则
A. B. C. D.
11.(6分)如图所示,、两轮绕轴转动,和两轮用皮带传动皮带不打滑,、、三轮的半径之比::,、、为三轮边缘上的点,则正确的是
A. 线速度
B. 角速度
C. 角速度
D. 向心加速度
12.(6分)学校门口的车牌自动识别系统如图所示,闸杆距地面高为,可绕转轴在竖直面内匀速转动;自动识别区到的距离为。汽车以速度匀速驶入自动识别区,识别的反应时间为;若汽车可看成高的长方体,闸杆转轴与车左侧面水平距离为。要使汽车匀速顺利通过,闸杆转动的角速度至少为
A. B. C. D.
13.(6分)一物体做匀速圆周运动的半径为,线速度大小为,角速度为,周期为下列关于这些物理量的关系式中,正确的是
A. B. C. D.
14.(6分)年北京冬奥会短道速滑比赛决出首枚金牌,男女米混合接力决赛,由范可新、曲春雨、任子威和武大靖出战的中国队,滑出分秒的成绩,获得中国代表团本届冬奥会的首枚金牌,也是短道速滑项目的首枚金牌。如图所示为我国选手武大靖在比赛中的精彩瞬间,假定他正沿圆弧形弯道做匀速圆周运动,则他运动过程中
A. 线速度恒定 B. 加速度恒定
C. 相等时间内经过的位移相同 D. 相等时间内转过的角度相同
二 、多选题(本大题共7小题,共42分)
15.(6分)两颗人造卫星绕地球做匀速圆周运动,它们的质量之比为,轨道半径之比,则下列说法正确的是
A. 它们的线速度之比为
B. 它们的向心加速度之比为
C. 它们的向心力之比为
D. 它们的周期之比为
16.(6分)小球做匀速圆周运动半径为,向心加速度为,则下列正确的是( )
A. 小球的角速度 B. 小球运动的周期
C. 时间内小球通过的路程 D. 时间内小球转过的角度
17.(6分)机器由电动机带动,机器皮带轮的半径是电动机皮带轮半径的倍,、为两轮边缘上的点,为机器皮带轮半径的中点,皮带与两轮之间不发生相对滑动,则下列说法正确的是
A. ,线速度大小之比
B. ,角速度大小之比
C. ,周期之比
D. ,向心加速度大小之比
18.(6分)一质点做匀速圆周运动,下列说法中正确的是
A. 任意相等时间内,通过的弧长相等
B. 任意相等时间内,转过的角度相等
C. 任意相等时间内,通过的位移相同
D. 任意相等时间内,速度的变化相同
19.(6分)如图所示是两个做圆锥摆运动的小球、小球,摆线跟竖直方向的夹角分别为和,两球做匀速圆周运动所在的水平面到各自悬点的距离之比为,下列有关判断正确的是( )
A. 两球运动周期之比为 B. 两球运动线速度之比为
C. 两球运动角速度之比为 D. 两球运动向心加速度之比为
20.(6分)甲、乙两个物体分别放在惠州和哈尔滨,将它们随地球一起转动的运动当作匀速圆周运动,下列说法正确的是
A. 甲的角速度一定较大
B. 甲的线速度一定较大
C. 甲的向心加速度一定较大
D. 甲所需的向心力一定较大
21.(6分)一半径为的球形行星绕其自转轴匀速转动,若质量为的物体在该星球两极时的重力为,在赤道上的重力为,则
A. 该星球自转的角速度大小为
B. 环绕该星球表面做匀速圆周运动的卫星的速率为
C. 环绕该星球表面做匀速圆周运动的卫星的速率为
D. 放置于此星球表面纬度为处的物体,向心加速度大小为
三 、简答题(本大题共3小题,共5分)
22.(5分)如图所示,轮、固定在一转轴上,轮、用皮带连接且不打滑。在、、三个轮的边缘各取一点、、,已知三个轮的半径比=,求:
22-1.、、三点的线速度大小之比。
22-2.、、三点的角速度之比。
22-3.、、三点的向心加速度大小之比。
答案和解析
1.【答案】A;
【解析】齿轮啮合,两齿轮边缘上各点的线速度大小相等,由题图可知甲、丙两轮边缘上各点的线速度大小相等。根据公式,得, 则丙轮的角速度大小,故选项A正确。
2.【答案】A;
【解析】解:、向心力的方向始终指向圆心,所以,向心加速度的方向也始终沿半径指向圆心,故A正确;
B、向心加速度的方向时刻指向圆心,方向改变,是变量,故B错误;
C、向心力总是垂直于速度,故只能改变物体的运动方向,不能改变物体运动速度的大小,故C错误;
D、物体做匀速圆周运动时,合力总是指向圆心,故又称向心力,是按照力的作用效果命名的,故D错误;
故选:.
做匀速圆周运动的物体要受到指向圆心的向心力的作用,从而产生指向圆心的向心加速度,向心加速度只改变物体的速度的方向不改变速度的大小.而非匀速圆周运动,合外力指向圆心的分量提供向心力.
匀速圆周运动要注意,其中的匀速只是指速度的大小不变,合力作为向心力始终指向圆心,合力的方向也是时刻在变化的.
3.【答案】A;
【解析】解:、是同轴转动角速度相同,根据,由图可知,可得,根据向心加速度公式,由图可知,可得,故正确,错误.
故选:.
4.【答案】D;
【解析】解:、由图线读得,转盘的转动周期,不变,故角速度,不变,故AB错误;
C、时刻的线速度:,时刻的线速度:,时刻的线速度:,
,解得,故C错误;
D、由于电脉冲信号宽度在逐渐变窄,表明光能通过狭缝的时间逐渐减少,即圆盘上对应探测器所在位置的线速度逐渐增加,因此激光器和探测器沿半径由中心向边缘移动,故D正确;
故选:。
由图得到圆盘的转动周期两次电脉冲信号的时间差,然后根据角速度定义公式求解圆盘转动的角速度;由图得到电脉冲信号宽度在逐渐变窄,说明线速度变大,结合公式进行判断即可。
考查圆周运动的角速度与周期的关系、角速度与线速度和半径关系,以及运用数学知识分析问题的能力,较难。
5.【答案】B;
【解析】
同轴传动角速度相等,同缘传动线速度相等,先结合判断后轮的角速度,然后再求解后轮边缘处点的线速度大小。
本题以某种品牌的共享单车为背景,考查链条传动问题,解决此题的关键是要明确同轴传动角速度相等,同缘传动线速度相等。
当踩踏板做匀速圆周运动的角速度为时,由于链轮与飞轮通过链条传动,边缘线速度大小相等,由公式可知,角速度与半径成反比,故飞轮的角速度为:,后轮的角速度与飞轮相等,可知后轮边缘处点的线速度大小为:,故正确,错误。
故选。
6.【答案】B;
【解析】
根据传动结构特点分析。
解答该题的关键是分析是哪一种转动,根据圆周运动解题。
A.自行车骑行时,后轮边缘的轮胎与飞轮的角速度相等,故A正确;
B.自行车拐弯时,由于前后轮的转弯半径不同,故前轮边缘与后轮边缘的线速度大小不相等,故B错误;
C.自行车上坡时,理论上采用中轴链轮最小挡,飞轮最大挡 ,线速度最小,最省力,故C正确;
D.自行车骑行时,链条相连接的飞轮边缘与中轴链轮边缘属于链条传动,故线速度大小相等,故D正确。
本题选不正确的,故选B。
7.【答案】A;
【解析】解:甲乙两物体角速度一样,同时由图可知:乙随地球转动的半径比甲小,根据:,可知甲的线速度大,故选项BCD错误,A正确。
故选:。
随地球自转的物体有两个共同点:一是角速度一样,二是圆心都在转轴上,根据这两点利用角速度和线速度关系即可求解。
该题考查了圆周运动中基本物理量角速度、线速度、半径之间关系,是一道基础性题目。
8.【答案】C;
【解析】分析:本题关键是明确同轴转动角速度相等,然后根据线速度与角速度关系公式比较线速度大小;也可以直接根据线速度和角速度的定义公式判断,基础题。
解答:跷跷板在转动时,横梁上、两点绕点转动属同轴转动,角速度相等,故有:
由于,根据,;
故正确,错误。
故选:。
同轴转动,角速度相等;根据判断线速度大小。
9.【答案】C;
【解析】解:.因为主动轮做顺时针转动,从动轮通过皮带的摩擦力带动转动,所以从动轮逆时针转动,故错误;
.由于通过皮带传动,皮带与轮边缘接触处质点的线速度相等,角速度不相等,故错误;
.根据得:
所以,故正确,错误.
故选:.
10.【答案】D;
【解析】解:杆上、两点绕点的转动属于同轴转动,所以角速度相等,故;
由于,根据,;故ABC错误,D正确。
故选:。
同轴转动,角速度相等;根据判断线速度大小。
本题关键是明确同轴转动角速度相等,然后根据线速度与角速度关系公式比较线速度大小;也可以直接根据线速度和角速度的定义公式判断,基础题。
11.【答案】D;
【解析】已知、、三轮的半径之间的关系;
、两个轮子是同轴传动,角速度相等,故,根据公式,线速度之比为;
根据公式,向心加速度之比为;
、两个轮子靠传送带传动,轮子边缘上的点具有相同的线速度,故::,根据公式,角速度之比为;
根据公式,可得。
A.结合以上分析结果可知,故错误;
角速度之比为,故、均错误;
D.三点的加速度之比为,故正确.
故选
12.【答案】A;
【解析】解:闸杆转动时间为
汽车匀速顺利通过,闸杆转动的角度至少为
解得
闸杆转动的角速度至少为,故正确,错误。
故选:。
求出汽车安全通过道闸时直杆转过的角度,然后求出直杆转动的角速度大小。
认真审题理解题意求出直杆转过的角度是解题的前提与关键,应用角速度的定义式即可解题。
13.【答案】D;
【解析】解:
、,故A错误,D正确;
、;故BC错误。
故选:。
直接根据线速度、角速度、周期的定义以及角度的定义出发展开讨论即可.
正确理解线速度的定义,角速度,弧长,能正确推导各量之间的关系是解决本题的关键.
14.【答案】D;
【解析】
、匀速圆周运动的线速度大小不变,方向在时刻发生变化,故错误;
、匀速圆周运动的加速度为向心加速度,大小保持不变,方向总是指向圆心,即加速度方向在时刻发生变化,故错误;
、匀速圆周运动的角速度保持不变,可知相等时间内转过的角度相同,对应的弦长相等,即经过的位移大小相等,但位移的方向不同,故错误,正确。
故选。
15.【答案】ABC;
【解析】
根据万有引力提供向心力,解出线速度、周期、角速度、加速度与轨道半径的关系,根据已知的半径求它们的比值。
此题主要考查了人造卫星的加速度、周期和轨道的关系。本题的关键是要掌握万有引力提供向心力,解出线速度、周期、加速度与轨道半径的关系。
根据万有引力提供向心力,解得:,,;所以:
A.根据,得,故正确;
B.根据,得,故正确;
C.根据,得,故正确;
D.根据,得,故错误。
故选。
16.【答案】BC;
【解析】.根据
可得,小球的角速度
A不符合题意;
B.根据
可得,小球运动的周期,符合题意;
C.根据,可得小球运动的速度
因此,时间内小球通过的路程,符合题意;
D.时间内小球转过的角度,不符合题意.
故答案为:.
17.【答案】BC;
【解析】
传动装置,在传动过程中不打滑,则有:共轴的角速度是相同的同一传动装置接触边缘的线速度大小是相等的所以当角速度一定时,线速度与半径成正比当线速度大小一定时,角速度与半径成反比因此根据题目条件可以知道加速度及角速度关系.
B.因与机器皮带边缘同轴转动,所以角速度相等,正确;
A.由,、角速度相同,所以,因电动机和机器由同一皮带连接,所以它们边缘线速度相等,所以,所以,错误;
C.因电动机和机器由同一皮带连接,所以它们边缘线速度相等设电动机半径为,角速度,机器轮半径为角速度为
根据题意知:,由得:所以,,由得:,正确;
D.由,,得:,错误。
故选。
18.【答案】AB;
【解析】该题有一定的综合性,在圆周运动中考察标量和矢量这两种物理量的特点,同时考察了匀速圆周运动的特点,用描述圆周运动的物理量和特点分析即可。
物理知识的学习过程中要前后融会贯通,不能是孤立的,明确各物理量的特点.如本题中在圆周运动中矢量、标量问题。A.匀速圆周运动中速度的大小不变,只是速度方向改变,因此在任意相等时间内,通过的弧长是相等的,故正确;匀速圆周运动角速度不变,可知相等时间转过的角度相等,故正确;C.位移大小等于由初位置指向末位置有向线段长度,线段的方向即为位移方向,是矢量,因此在任意相等时间内,位移不一定相同,故错误;
速度是矢量,速度的变化量为,方向由指向即减数指向被减数,因此在任意相等时间内速度的变化不一定相同,故错误。故选。
19.【答案】ACD;
【解析】由题可知,可以设两个小球的质量都是;设球做匀速圆周运动所在的水平面到悬点的距离为,则球做匀速圆周运动所在的水平面到悬点的距离为,则球做圆周运动的半径:==,球做圆周运动的半径:=
以球为研究对象,根据重力与绳子的拉力的合力提供向心力,可得:=,解得:
同理,以球为研究对象,可得:
、两球运动的角速度之比:,根据,两球的周期之比:,故正确;
、两球的线速度之比:,故错误;
、根据公式:=.则:,故正确。
20.【答案】BC;
【解析】
地球上的任何的物体转动的角速度都和地球一样,但是在不同的地方,由于物体做圆周运动的半径不一样,线速度的大小不一样。随着地球一起绕地轴转动,说明它们的角速度是一样的,这是解本题的关键条件,再由线速度角速度的关系就可以做出判断了。
地球上的任何的物体转动的角速度都和地球一样,但是在不同的地方,由于物体做圆周运动的半径不一样,线速度的大小不一样,甲的半径大,线速度一定较大,故错误,正确;C.向心加速度,甲的向心加速度一定较大,故正确;
D.甲乙两个质量不知道大小,无法确定所需的向心力大小,故错误。
故选。
21.【答案】ACD;
【解析】
在两极,万有引力等于重力,在赤道,万有引力的一个分力等于重力,另一个分力提供向心力,结合牛顿第二定律求出星球自转的角速度.根据万有引力等于重力、万有引力提供向心力求出环绕星球表面做匀速圆周运动的卫星速率.根据几何关系求出在星球表面纬度为处物体转动的半径,结合向心加速度公式求出向心加速度的大小。
解决本题的关键知道在两极和赤道处万有引力和重力的关系,掌握万有引力定律的两个重要理论,并能灵活运用,难度中等。
A.在两极,万有引力等于重力,有:,在赤道,有:,联立两式解得,故正确;
根据得,,又,解得,故错误,正确;
D.处于星球表面纬度为处的物体,绕地轴转动的半径,则向心加速度,故正确。
故选。
22.【答案】、、三点的线速度大小之比=。;、、三点的角速度之比=。;、、三点的向心加速度大小之比=。;
【解析】、两点靠传送带传动,线速度大小相等,、共轴转动,角速度相等,根据=,则==。
所以、、三点的线速度大小之比=。
、共轴转动,角速度相等,、两点靠传送带传动,线速度大小相等,根据=,==.所以、、三点的角速度之比=。
、的线速度相等,根据,知==.、的角速度相等,根据=得,==.所以、、三点的向心加速度大小之比=。
